K-means算法与K-means++算法的异同

经典Kmeans算法是最常用的一种聚类算法。感觉在西瓜书里面最容易看懂的，而且最容易用的一个算法便是k-mean算法，算法实现的流程十分简单，可以简单将其划分为4个步骤：

Step1:选定聚类中心，从数据集中随机选取K个样本作为初始聚类中心，{}, i = 1, 2, 3, 4, 5, ... n ;

Step2:计算欧式距离，并对其进行归类，遍历数据集中的每一个样本，计算每一个样本与所有初始聚类中心的欧式距离，将其加入到欧式距离最小的那个聚类中心的一类中

Step3:更新聚类中心，重新计算每一类的中心，, n每一个类中的样本个数

Step4: 重新聚类，重新遍历数据集中的每一个样本，计算每一个样本与所有新的聚类中心的欧式距离，将其加入到欧式距离最小的那个聚类中心的一类中

不断重复上面四个步骤，直至聚类中心不再改变，聚类停止。

 K-means++算法：

K-means++算法是基于传统K-means的改进版，改进的地方在于，它的聚类中心不是随机产生的，而是在一开始就已经通过一种十分有效的方式给选出来了,但是有一点仍旧是需要给出初始的第一个聚类中心，第一个聚类中心是随机产生的。

对K-means++算法原理进行简单总结一下：

        首先，其实的簇中心是我们通过在样本当中随机得到的。不过我们并不是一次性随机K个，而是只随机1个。

        接着，我们要从生下的n-1个点当中再随机出一个点来做下一个簇中心。但是我们的随机不是盲目的，我们希望设计一个机制，使得距离所有簇中心越远的点被选中的概率越大，离得越近被随机到的概率越小。

        我们重复上述的过程，直到一共选出了K个簇中心为止。

K-menas++便是针对这个机制提出了一个有效的方法，比较简单的称为轮盘法，下面简单介绍一下：

        我们来看一下如何根据权重来确定概率，实现这点的算法有很多，其中比较简单的是轮盘法。这个算法应该源于赌博或者是抽奖，原理也非常相似。

        我们或多或少都玩过超市或者是其他场景下的转盘抽奖，在抽奖当中有一个指针一直保持不动。我们转动转盘，当转盘停下的时候，指针所指向的位置就是抽奖的结果。

我们都知道命中结果的概率和轮盘上对应的面积有关，面积越大抽中的概率也就越大，否则抽中的概率越小。

对于每一个点，被选中的概率为：

 

其中是每个点到所有类簇的最短距离，表示点被选中作为类簇中心的概率。

轮盘法其实就是一个模拟转盘抽奖的过程，只不过我们用数组模拟了转盘。我们把转盘的扇形拉平，拉成条状，原来的每个扇形就对应了一个区间。扇形的面积就对应了区间的长度，显然长度越长，抽中的概率越大。然后我们来进行抽奖，我们用区间的长度总和乘上一个0-1区间内的数。

我们找到这个结果落在的区间，就是这次轮盘抽中的结果。这样我们就实现了控制随机每个结果的概率。

 

在上面这张图当中，我们随机出来的值是0.68，然后我们一次减去区间，最后落到的区间

上面讲的可能比较抽象，借助我看过的一篇论文，将基本思想从论文上摘下来加强大家的理解，其思想可简单理解为: 选定一个聚类中心后，当要确定下一个聚类中心的时候，将计算其它所有样本点与聚类中心的距离 d(x) ，将所有的距离d(x)组成一个集合 D，把集合 D中的每个元素d(x)想象为一根线L(x)，线的长度就是d(x) 。将这些线依次按照L(1)，L(2) ，…，L(n)的顺序连接起来，组成一根长线 L，L( 1) ，L( 2) ，…，L( n) 称 为 L 的子线。根据概率的相关知识，如果在L上随机选择一个点，那么这个点很可能落在比较长的子线 上，而这个子线对应的数据点就可以作为新的种子点。

下面结合一个简单的例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本，分布以及对应序号如下图所示：

 

图3. K-means++示例

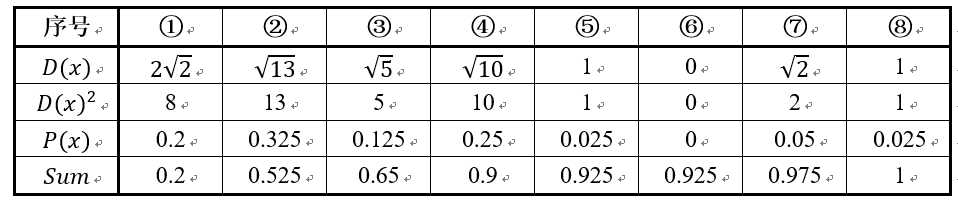
 假设经过图2的步骤一后6号点被选择为第一个初始聚类中心，那在进行步骤二时每个样本的D(x)和被选择为第二个聚类中心的概率如下表所示：

其中的P(x)就是每个样本被选为下一个聚类中心的概率。最后一行的Sum是概率P(x)的累加和，用于轮盘法选择出第二个聚类中心。方法是随机产生出一个0~1之间的随机数，判断它属于哪个区间，那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2)，2号点的区间为[0.2, 0.525)。

      从上表可以直观的看到第二个初始聚类中心是1号，2号，3号，4号中的一个的概率为0.9。而这4个点正好是离第一个初始聚类中心6号点较远的四个点。这也验证了K-means的改进思想：即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。

        针对于python语言,已经有相关的官网有相关与K-means与K-means++相关算法的库，可以直接调用，但是当遇到多维特征向量的时候不容易直接调用，就比较难直接调用这些库实现，所以可以考虑对原理进行理解，自己编写代码尝试一下，因为K-menas也算是比较简单的算法啦，写起来也不是十分困难。

借鉴到的文章：

https://www.cnblogs.com/yixuan-xu/p/6272208.html

Kmeans加权聚类和多维聚类可视化 - 知乎