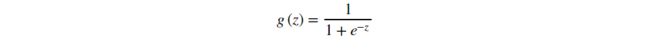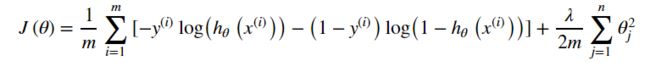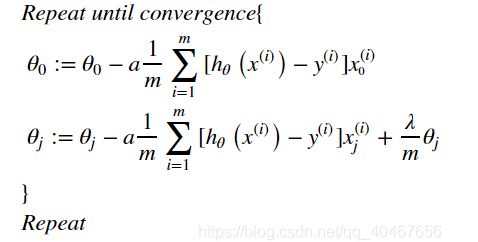【吴恩达】机器学习作业 ex3data1 -- 多分类逻辑回归（Python）

一.前言

        本次是多分类逻辑回归的代码，主题是让你预测5000个手写数字对应的真正数字，每张图片有400个特征值，可以用20*20的方阵表示出来，一共5000行数据，此次的数据集是.mat类型，和以往的txt的导入会不同。

二.代码解析

1.导入工具包

        这里注意看，我们需要导入一个scipy包，利用其loadmat()方法来将ex3data1.mat进行导入，以往所使用的pandas包就不需要了,scipy包的导入不会的可以看我第一章博客，里面有包的导入方法。

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat

2.导入数据与初始化

        loadmat方法取出的数据，返回的类型为字典，字典中有几个key值，其中X就代表了400个特征值，y就代表了手写数字图片所对应的真正的阿拉伯数字，同样的将X，y变为矩阵以后，还是在X的第一列插入1，这样方便与矩阵theta进行运算，此时X_add1的维度为（5000*401)，theta初始化为（401 * 1）的零矩阵

# 用loadmat取出数据，因为这里是matlob的格式文档，所以用scipy库的loadmat方法取出，返回的是字典形式
data = loadmat('ex3data1.mat')
# print(data)  # 看一下data是否导入成功
# print(data['X'].shape,data['y'].shape)  # 看一下X和y俩列的维度
X = data['X']
y = data['y']
# print(X,type(X))  # 查看类型
# print(y,type(y))
X = np.matrix(X)
y = np.matrix(y)
X_add1 = np.matrix(np.insert(data['X'], 0, values=np.ones(5000), axis=1))  # 在X的第一列加入1，方便和theta进行矩阵相乘
theta = np.matrix(np.zeros((401, 1)))

3.随机打印一个数字

        我们首先要抽取一行数据，将这一行数据中400个特征值重塑为20*20的方阵，我说一下为什么要重塑为方阵的原因，可以将这400个数据想象成400个小方块，而这400个小方块又组成一个20*20维度的大方块，也就是正方形图片，其中值为0的小方块就可以默认为白色背景，那有数值的小方块就是有颜色的部分，这个matshow（）的方法就是随着数值的增大，颜色变得越来越深，那就可以得到一个由多个带有颜色的小方块组成了一张图片（这里我将画布调大一些，鼠标停留在不同位置时，可以清晰的看到数值的变化）

# 随机打印一个数字
def plot_one():
    any_num = np.random.randint(0, 5000)  # 随机取一个0-5000之内的一个数
    X_new = X[any_num].reshape(20, 20)  # 随机取出一行设其为一个20*20维度的矩阵
    print(f'这是：{y[any_num, :]}')  # 找出对应的数字
    fig, ax = plt.subplots(figsize=(8, 8))  # 我将画布放大了更便于鼠标停留观察
    # 这里可以理解为一共有400个小方格，只有有值的方格才会被突出颜色，为零的都是背景，
    # 所以由于设置方阵的方法不同，数值的位置也会相应不同，数字会七扭八歪
    # 注意，这里数值高的部分会颜色深一些，相对数值低的颜色较浅，这也就是为什么有值的才会突出颜色
    ax.matshow(X_new, cmap='Blues')  # 这里matshow是展示出这个20*20的矩阵，数值为0的为空白，有值的为就方格图色
    plt.xticks([])  # 剔除x轴的刻度
    plt.yticks([])  # 剔除y轴的刻度
    plt.show()
    pass

这里直接调用plot_one的方法即可 

 

 4.随机打印100个数字

        这个和上面的随机打印一个数字还是有一些区别的，首先利用np.random.choice来取出0-5k之内100个数，然后在X中和y中将其截取出来，首先做一个8*8的大画布，里面在放100个小画布，nrows与ncols就代表了10行*10列 = 100个子图，每个子图都可以用ax[i][k]的方式去布置，比如ax[0][0]意思就是取出第一个画布，同样X_new里存放着100行数据，每行有400个特征值，随着100次迭代，将每一行的数据全部取出，并重塑为20*20的方阵，设置好颜色即可，代码图和效果图如下：

# 随机打印100个数字
def plot_hundred():
    numbers_show = []
    any_hudwords = np.random.choice(range(0, 5000), 100)  # 因为要取100个数字所以用np.random.choice,返回的是ndarray数组类型
    # X[]的意思是默认取any_hudwords所选取的100行
    X_new = X[any_hudwords]
    # y[]也同理
    y_new = y[any_hudwords]
    # 这里nrows和ncols分别代表了行和列，也就是含有10*10一百个子图，控制这些子图的方式就是ax，取第一个子图那就是ax[0][1]
    fig, ax = plt.subplots(figsize=(8, 8), nrows=10, ncols=10, sharex=True, sharey=True)
    for i in range(10):
        for k in range(10):
            # 下面代表的是每个子图都进行填充，X_new从第一行取到lues第100行，每行400个数据初始化为20*20的方阵，颜色设置为Blues
            ax[i][k].matshow(X_new[i * 10 + k].reshape(20, 20), cmap='Blues')
    print(y_new.reshape(1, 100))  # 将选取的100个数据所对应的数值用1*100的维度输出（便于观察）
    plt.xticks([])  # 剔除x轴的刻度
    plt.yticks([])  # 剔除y轴的刻度
    plt.show()
    pass

这里直接调用该方法即可 

对应阿拉伯数字如下 

 5.sigmoid假设函数

        老样子，还是为了将数据控制在0-1之间，方便判断，这块不懂得可以看我主页逻辑回归第一个任务ex2data1

# 假设函数（也是边界线判断）
def sigmod(z):
    return 1 / (1 + np.exp(-z))
    pass

6.代价函数

        同样代价函数，在逻辑回归第一个任务也有提到，此处无变化，直接用即可，简单说一下就是分为三部分，前俩个log函数合并为一个函数，y无论是0还是1都只会执行一部分，另一部分会变为0，最后加一项正则项

# 代价函数
def cost_fuc(X_add1, y, theta, lamda):
    first = -(np.multiply(np.log(sigmod(X_add1 @ theta)), y).sum())  # 第一项
    second = -(np.multiply(np.log(1 - sigmod(X_add1 @ theta)), (1 - y)).sum())  # 第二项
    regular = (lamda / (2 * len(X))) * np.power(theta, 2).sum()  # 正则一项
    return (first + second) / len(X) + regular
    pass

7.梯度下降函数

        这里梯度下降不需要对theta0进行惩罚，j是从1开始惩罚，所以分为2种情况，代码的话也分为俩部分，首先先将theta整个矩阵与前面的公式剥离开来，与系数相乘，同时把theta0设置为0，这样在与更新之后的theta相加的时候就可以做到不对theta0进行乘法，也进行了正则化，一步步的缩小theta的值

# 梯度下降函数
def gradient_fuc(X_add1, y, theta, lamda, update_times):
    for i in range(update_times):
        reg_theta = (lamda / len(X_add1)) * theta
        reg_theta[0] = 0  # 不惩罚theta0
        theta = theta - (1 / len(X_add1) * (X_add1.T @ (sigmod(X_add1 @ theta) - y)))  # 第一项求导为1
        theta = theta + reg_theta
    return theta
    pass

8.一对多逻辑判断

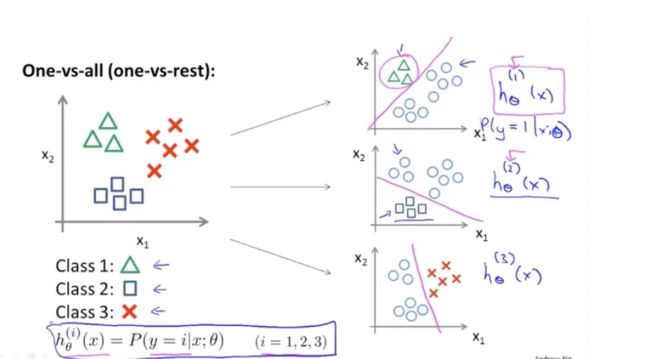
        核心思想：多分类逻辑回归的根本就是将其中一个结果设为1，其他结果都设置为0，也就是除了当前判断的数字之外都默认为判断错误，同时求出当前最符合的theta矩阵

         代码讲解：首先将theta_sum设置为一个10*401维度的矩阵，可知我们每次所得的theta都是401*1维度的矩阵，一共十个分类器（1-10），那就是说会得到10个theta矩阵，我们将其整合到theta_sum 当中去，为以后预测数据的矩阵相乘来做准备。第一个for循环是用来求出10个分类器的theta矩阵，第二个for循环用来将每一类都与其他类相分离，当前需要预测就设为1，其他结果设为0，将这些数据放进y_classify暂时存放，充当一个y矩阵的复制品，里面只有0和1俩种状态。

# 一对多判断
def one_vs_all(theta, X_add1, y, lamda , update_times):
    theta_sum = np.matrix(np.zeros((10, 401)))  # 将各个theta的总矩阵设置乘 10*401 维度
    for i in range(1, 11):  # 1-10，一共十个分类，循环十次，每循环一次都是 1vs其他
        y_classify = []  # 设置一个y在循环当中的替换容器，这里存放着本次要判断的结果
        for k in y:
            if k == i:
                y_classify.append(1)  # 命中为 1
            else:
                y_classify.append(0)  # 未命中为 0
        y_classify = np.array(y_classify).reshape(5000, 1)  # 将此替代器进行塑性，提高维度，1维度列表变为5000*1的矩阵
        theta_i = gradient_fuc(X_add1, y_classify, theta, lamda, update_times)  # 梯度下降函数得出每次的theta的矩阵
        theta_sum[i-1] = theta_i.T  # 这里因为我们得到的是401 * 1的theta矩阵，所以需要重新塑性为1*401放入总的theta矩阵的每一行中（10*401）
    # print(theta_sum)
    return theta_sum
    pass

theta_sum (这里用了400次迭代)

9.预测函数

        下面是p_matrix矩阵的由来，简单的推理过程

        现在可知p_matrix里面每一行都存放了对1-10的预测hx值，那么肯定是这一行中值最大的就是最有可能的答案，这里利用np.argmax找出每行中最大值得下标，返回得是是一个（5000，）类型得矩阵， 我们将其重塑为5000*1维度的矩阵，这样方便和y矩阵进行判断，for循环进行判断之后记录预测对的结果数，与总数相比得到预测成功率

        注意：这里返回的下标是从零开始的，所以要+1再与y矩阵进行比较

# 预测函数
def predict_fuc(theta_sum, X_add1, y):
    p_matrix = sigmod(X_add1 @ theta_sum.T)  # 总的概率矩阵，维度为（5000*10），每一列的名字都可以当作是预测数值，注意从0开始
    p_max= np.argmax(p_matrix,axis=1)  # 搜索每一行的最大值并返回其下标，一共5000行，返回5000个预测的最大概率的下标
    p_max = np.matrix(p_max.reshape(5000,1) + 1)  # 将其重塑为一个5000 * 1维度的矩阵，并所有值加一，因为默认矩阵是从0开始的
    print(p_max,p_max.shape)
    count = 0  # 计数器
    for i in range(0,5000):
        if p_max[i] == y[i]:
            count = count + 1
    return count / len(y)
    pass

10.运行

        我第一次设置的是400次的迭代，成功率大约为91-92之间，将迭代次数设置为1万之后数据变得更准确，能达到95-96之间，和答案的94左右有些差距，大家也可以自行尝试

theta_sum = one_vs_all(theta, X_add1, y, 0.01,10000)
print(f'预测率为：{predict_fuc(theta_sum, X_add1, y)}')

三.全部代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat

# 用loadmat取出数据，因为这里是matlob的格式文档，所以用scipy库的loadmat方法取出，返回的是字典形式
data = loadmat('ex3data1.mat')
# print(data)  # 看一下data是否导入成功
# print(data['X'].shape,data['y'].shape)  # 看一下X和y俩列的维度
X = data['X']
y = data['y']
# print(X,type(X))  # 查看类型
# print(y,type(y))
X = np.matrix(X)
y = np.matrix(y)
X_add1 = np.matrix(np.insert(data['X'], 0, values=np.ones(5000), axis=1))  # 在X的第一列加入1，方便和theta进行矩阵相乘
theta = np.matrix(np.zeros((401, 1)))


# 随机打印一个数字
def plot_one():
    any_num = np.random.randint(0, 5000)  # 随机取一个0-5000之内的一个数
    X_new = X[any_num].reshape(20, 20)  # 随机取出一行设其为一个20*20维度的矩阵
    print(f'这是：{y[any_num, :]}')  # 找出对应的数字
    fig, ax = plt.subplots(figsize=(2, 2))  # 我将画布放大了更便于鼠标停留观察
    # 这里可以理解为一共有400个小方格，只有有值的方格才会被突出颜色，为零的都是背景，
    # 所以由于设置方阵的方法不同，数值的位置也会相应不同，数字会七扭八歪
    # 注意，这里数值高的部分会颜色深一些，相对数值低的颜色较浅，这也就是为什么有值的才会突出颜色
    ax.matshow(X_new, cmap='Blues')  # 这里matshow是展示出这个20*20的矩阵，数值为0的为空白，有值的为就方格图色
    plt.xticks([])  # 剔除x轴的刻度
    plt.yticks([])  # 剔除y轴的刻度
    plt.show()
    pass


# 随机打印100个数字
def plot_hundred():
    numbers_show = []
    any_hudwords = np.random.choice(range(0, 5000), 100)  # 因为要取100个数字所以用np.random.choice,返回的是ndarray数组类型
    # X[]的意思是默认取any_hudwords所选取的100行
    X_new = X[any_hudwords]
    # y[]也同理
    y_new = y[any_hudwords]
    # 这里nrows和ncols分别代表了行和列，也就是含有10*10一百个子图，控制这些子图的方式就是ax，取第一个子图那就是ax[0][1]
    fig, ax = plt.subplots(figsize=(8, 8), nrows=10, ncols=10, sharex=True, sharey=True)
    for i in range(10):
        for k in range(10):
            # 下面代表的是每个子图都进行填充，X_new从第一行取到lues第100行，每行400个数据初始化为20*20的方阵，颜色设置为Blues
            ax[i][k].matshow(X_new[i * 10 + k].reshape(20, 20), cmap='Blues')
    print(y_new.reshape(1, 100))  # 将选取的100个数据所对应的数值用1*100的维度输出（便于观察）
    plt.xticks([])  # 剔除x轴的刻度
    plt.yticks([])  # 剔除y轴的刻度
    plt.show()
    pass


# 假设函数（也是边界线判断）
def sigmod(z):
    return 1 / (1 + np.exp(-z))
    pass


# 代价函数
def cost_fuc(X_add1, y, theta, lamda):
    first = -(np.multiply(np.log(sigmod(X_add1 @ theta)), y).sum())  # 第一项
    second = -(np.multiply(np.log(1 - sigmod(X_add1 @ theta)), (1 - y)).sum())  # 第二项
    regular = (lamda / (2 * len(X))) * np.power(theta, 2).sum()  # 正则一项
    return (first + second) / len(X) + regular
    pass


# 梯度下降函数
def gradient_fuc(X_add1, y, theta, lamda, update_times):
    for i in range(update_times):
        reg_theta = (lamda / len(X_add1)) * theta
        reg_theta[0] = 0  # 不惩罚theta0
        theta = theta - (1 / len(X_add1) * (X_add1.T @ (sigmod(X_add1 @ theta) - y)))  # 第一项求导为1
        theta = theta + reg_theta
    return theta
    pass


# 一对多判断
def one_vs_all(theta, X_add1, y, lamda , update_times):
    theta_sum = np.matrix(np.zeros((10, 401)))  # 将各个theta的总矩阵设置乘 10*401 维度
    for i in range(1, 11):  # 1-10，一共十个分类，循环十次，每循环一次都是 1vs其他
        y_classify = []  # 设置一个y在循环当中的替换容器，这里存放着本次要判断的结果
        for k in y:
            if k == i:
                y_classify.append(1)  # 命中为 1
            else:
                y_classify.append(0)  # 未命中为 0
        y_classify = np.array(y_classify).reshape(5000, 1)  # 将此替代器进行塑性，提高维度，1维度列表变为5000*1的矩阵
        theta_i = gradient_fuc(X_add1, y_classify, theta, lamda, update_times)  # 梯度下降函数得出每次的theta的矩阵
        theta_sum[i-1] = theta_i.T  # 这里因为我们得到的是401 * 1的theta矩阵，所以需要重新塑性为1*401放入总的theta矩阵的每一行中（10*401）
    print(theta_sum)
    return theta_sum
    pass


# 预测函数
def predict_fuc(theta_sum, X_add1, y):
    p_matrix = sigmod(X_add1 @ theta_sum.T)  # 总的概率矩阵，维度为（5000*10），每一列的名字都可以当作是预测数值，注意从0开始
    p_max= np.argmax(p_matrix,axis=1)  # 搜索每一行的最大值并返回其下标，一共5000行，返回5000个预测的最大概率的下标
    p_max = np.matrix(p_max.reshape(5000,1) + 1)  # 将其重塑为一个5000 * 1维度的矩阵，并所有值加一，因为默认矩阵是从0开始的
    print(p_max,p_max.shape)
    count = 0  # 计数器
    for i in range(0,5000):
        if p_max[i] == y[i]:
            count = count + 1
    return count / len(y)
    pass


theta_sum = one_vs_all(theta, X_add1, y, 0.01,10000)
print(f'预测率为：{predict_fuc(theta_sum, X_add1, y)}')