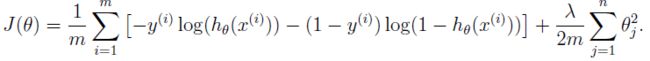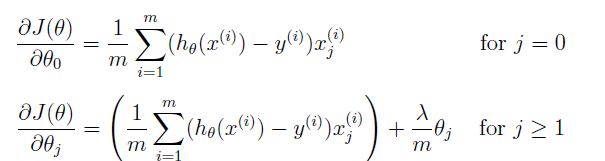吴恩达机器学习ex3

第一部分 多分类问题

题目介绍：使用逻辑回归识别0到9的手写数字

数据集：5000个手写数字的训练样本，每一个训练样本都是20像素×20像素的灰度图像的数字，每个像素由一个表示该位置灰度强度的点编号表示，这个20x20的像素网格被“展开”成一个400维的向量。每一个训练样本都是矩阵X的一行数据，这就得到了一个5000×400矩阵X，其中每一行都是一个手写数字图像的训练示例。
训练集的第二部分是一个5000维的向量y，包含了训练集的标签，由于octave/MATLAB中没有0的索引，数字‘0’用标签‘10’代替。

1.数据可视化

代码从X中随机选择100行，构成一个100×400的新矩阵来作图，导入的时候就将构成一张图的矩阵展开为1*400的行向量。

% Randomly select 100 data points to display
rand_indices = randperm(m);
sel = X(rand_indices(1:100), :);

displayData(sel);

displayData(sel);传入一个100*400的矩阵

function [h, display_array] = displayData(X, example_width)
% Set example_width automatically if not passed in
if ~exist('example_width', 'var') || isempty(example_width) 
	example_width = round(sqrt(size(X, 2))); % example_width = 20
end

如果函数要求的example_width变量不存在，使用X列数的算术平方根来定义，我们使用该函数时并没有传入这一变量，因此example_width = 20。

% Compute rows, cols
[m n] = size(X); %m = 100; n =400
example_height = (n / example_width); % example_height = 20

% Compute number of items to display
display_rows = floor(sqrt(m)); % display_row =10
display_cols = ceil(m / display_rows); % display_cols =10

% Between images padding
pad = 1;

% Setup blank display
display_array = - ones(pad + display_rows * (example_height + pad), ...
                       pad + display_cols * (example_width + pad));

这一部分主要是一些初始化的工作

% Copy each example into a patch on the display array
curr_ex = 1;
for j = 1:display_rows % 1到10
	for i = 1:display_cols % 1到10
		if curr_ex > m,  % 不超过100
			break; 
		end
		% Copy the patch
		
		% Get the max value of the patch
		% 取 X 每一行的最大值方便后面进行按比例缩小（暂且称为标准化）
		max_val = max(abs(X(curr_ex, :)));
		% 把原先的 X 里面每行标准化以后按 20 * 20 的形式 替代 display_array 中的元素
		display_array(pad + (j - 1) * (example_height + pad) + (1:example_height), ...
		              pad + (i - 1) * (example_width + pad) + (1:example_width)) = ...
						reshape(X(curr_ex, :), example_height, example_width) / max_val;
		curr_ex = curr_ex + 1;
	end
	if curr_ex > m, 
		break; 
	end
end

这一部分的代码就是逐行逐列地将每个小图的矩阵传入display_array。举例 curr_ex = 1, i = 1， j = 1，display_array ( 1 + 0 * 21 + (1:20), 1 + 0 * 21 + (1:20))
也就是disoplay_array((2:21),(2:21)) = reshape(X(1,:), 20, 20) / max_val;这就得到图中的第一个小图‘6’。

2.向量化逻辑回归

使用one-vs-all的逻辑回归模型建立多分类器。10个类别就需要分别训练10个逻辑回归分类器。向量化的代码中不含任何循环。

2.1 向量化损失函数

首先是逻辑回归中的损失函数公式：

我们定义X和θ如下：

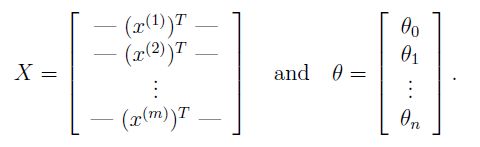
我们知道训练样本有5000个，每个样本有400个“特征“”（20像素×20像素），相当于5000*400的矩阵，我们把每个样本的特征，也就是一个列向量拿出来，转置后为一个行向量，才能够和参数θ（列向量）相乘。
两个矩阵相乘可以得到：

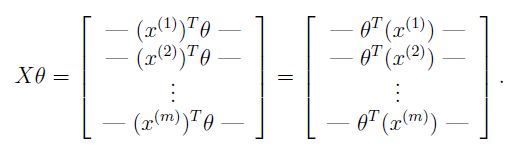
2.2 向量化梯度

逻辑回归中的梯度公式：

θ是一个列向量，那么每一个θ_j的梯度组成的也是一个列向量：

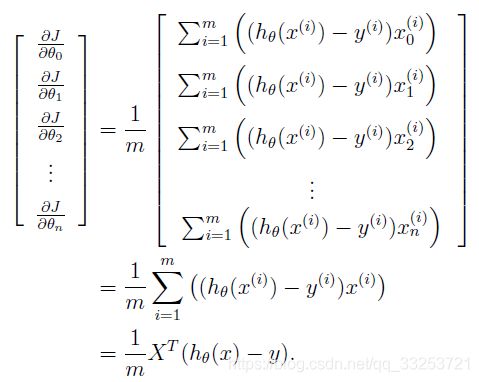
下面说明如何得到最后一步，我们知道：

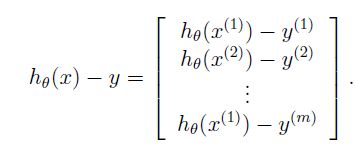
这里的xi是一个向量，而h_θ(xi)-y是一个标量（一个数字），我们定义β_i = h_θ(xi)-y：

上述的结论使我们可以不使用循环去计算每一个偏导数

2.3 向量化正则化逻辑回归

正则化损失函数公式：

正则化梯度公式：

实现代码：

J = (1/m) * (-y'*log(sigmoid(X*theta)) - (1-y)'*log(1-sigmoid(X*theta))) + lambda / (2*m) * sum(theta(2:end).^2);
grad = (1/m) * X' *(sigmoid(X*theta)-y);
temp = theta; 
temp(1) = 0;   % because we don't add anything for j = 0  
grad = grad + lambda/m *temp; %(using the temp variable)

3.One-vs-all分类

下面训练多个正则化逻辑回归分类器，返回值是一个关于θ的矩阵，矩阵的每一行参数对应一个分类器，如果有K的类别，可以使用循环1到K单独训练每个分类器。
另外，使用fmincg优化。

% Some useful variables
m = size(X, 1); % 行数5000
n = size(X, 2); % 列数400

% You need to return the following variables correctly 
all_theta = zeros(num_labels, n + 1); % 10*401

% Add ones to the X data matrix
X = [ones(m, 1) X]; % 5000*401
options = optimset('GradObj', 'on', 'MaxIter', 50);
for c = 1:num_labels
  all_theta(c,:)=fmincg(@(t)(lrCostFunction(t, X, (y==c), lambda)), all_theta(c,:)', options)';
end

all_theta是一个10401的矩阵，对应10个分类器，每一行1401对应一个分类器。X是一个5000401的矩阵，因此函数中计算时需要转置为4011的列向量，得到新的401个θ参数，最终得到再转置为行向量。

4.预测

对于每一个输入，计算对应每一个分类器的概率，最终选择概率最高的那个分类器。

A = sigmoid(X * all_theta'); % 计算概率
[X, index] = max(A, [], 2); % 得到最大值以及其索引
p = index;

计算准确率

%% ================ Part 3: Predict for One-Vs-All ================

pred = predictOneVsAll(all_theta, X);

fprintf('\nTraining Set Accuracy: %f\n', mean(double(pred == y)) * 100);

和之前的练习一样，判断预测值和真实值是否相同，相同的置1，不同的置0，再用相同的个数除以总量。

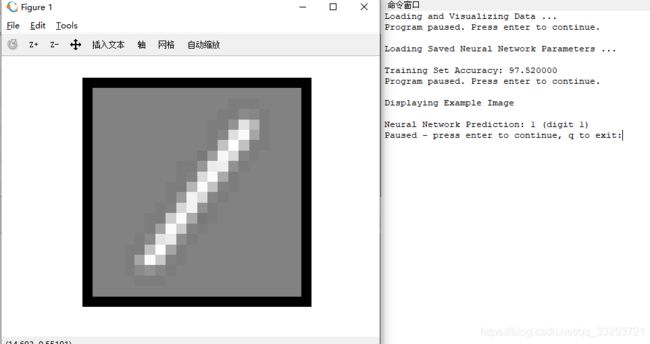
第二部分 神经网络

神经网络模型：

该神经网络模型有三层——一个输入层，一个隐藏层，一个输出层。由于图片的尺寸是20×20，因此输出层单元就有401个（加上一个偏置单元）。
神经网络的两个参数θ_1和θ_2已经给出，该网络在第二层有25个单元，输出层有10个单元（对应10个分类）。
θ_1：25×401，θ_2：10×26.
我们只需要根据给出的神经网络编写代码：

X = [ones(m, 1) X];
z2 = X * Theta1';
a2 = sigmoid(z2);
a2 = [ones(m, 1) a2];
z3 = a2 * Theta2';
a3 = sigmoid(z3);
[X, index] = max(a3, [], 2);
p = index;

结果：