【推荐系统】推荐系统基础算法-基于协同的推荐算法
目录
基于物品的协同过滤
计算物品之间的相似度
（1）基于共同喜欢物品的用户列表计算
同时被购买次数矩阵
（2）基于余弦的相似度计算
（3）热门物品的惩罚
计算用户u对于物品i的预测分数
基于用户的协同算法
计算用户相似度
计算得分
基于用户协同和基于物品协同的区别
基于内容的推荐方法缺陷：
- 内容必须能够抽取有意义的特征，并要求这些特征内容具有良好的结构性
- 推荐精度较低，相同内容特征的物品差异性不大
因此，基于内容的推荐往往会和其他方法混用，比如基于邻域的算法， 基于邻域的算法可以分为
- 基于用户的协同过滤
- 基于物品的协同过滤
协同过滤算法具有速度快和准确率高两种特点
基于物品的协同过滤
基于物品的协同过滤的核心：给用户推荐那些和他们之前喜欢的物品相似的物品
当你购买了笔记本电脑，系统会推荐给你鼠标或键盘，不同于内容推荐，基于物品的协同过滤中的相似，指的是用户行为的相似
计算物品之间的相似度
基于物品的协同算法首先计算物品之间的相似度，计算相似度的方法有以下几种。
（1）基于共同喜欢物品的用户列表计算
例如上面当当网给出的理由是“经常一起购买”。通过公式计算一起购买的方法是
分母中N(i) 是购买物品i的用户数，N(j)是购买物品j的用户数，而分子是同时购买物品i和物品j的用户数。上述的公式的核心是计算同时购买这两本书的人数比例。当同时购买这两个物品人数越多，他们的相似度也就越高。
在分母中我们用了物品总购买人数做惩罚，也就是说某个物品可能很热门，导致它经常会被和其他物品一起购买，所以除以它的总购买人数，来降低它和其他物品的相似分数。举例来说，用户A对物品i1、i2、i4有购买行为，用户B对物品i2、i4有购买行为等。
同时被购买次数矩阵
NxN的矩阵C，存储物品两两同时被购买的次数。遍历每个用户的购买历史，当i和j两个物品同时被购买时，则在矩阵C中(i,j)的位置上加1。当遍历完成时，则可得到共现次数矩阵C，其中，C[i][j]记录了同时喜欢物品i 和物品 j 的用户数，这样我们就可以得到物品之间的相似度矩阵W。
| i1 | i2 | i3 | i4 | i5 | |
| i1 | 2 | 1 | 1 | ||
| i2 | 2 | 1 | 2 | 1 | |
| i3 | 1 | ||||
| i4 | 1 | ||||
| i5 | 1 | 1 |
#ItemCF算法
def ItemSimilarity(train):
C = dict() #书本同时被购买的次数
N = dict() #书本被购买的用户数
for u,items in train.items():
for i in items.keys():
if i not in N.keys():
N[i] = 0
N[i] +=1
for j in items.keys():
if i == j:
continue
if i not in C.keys():
C[i] = dict()
if j not in C[i].keys():
C[i][j] == 0
#当用户同时购买了i和j，则加1
C[i][j] += 1
W = dict()#书本对相似分数
for i ,related_items in C.items():#i为物品
if i not in W.keys():
W[i] = dict()
for j ,cij in related_items.items():
W[i][j] = cij/math.sqrt(N[i] * N[j])
return W
if __name__ =='___main__':
Train_Data = {'A':{'i1':1,'i2':1,'i4':1},
'B':{'i1':1,'i4':1},
'C':{'i1':1,'i2':1,'i5':1},
'D':{'i2':1,'i3':1},
'E':{'i3':1,'i5':1},
'F':{'i2':1,'i4':1},
}
W = ItemSimilarity(Train_Data)运行代码，得到物品间的相似度矩阵
（2）基于余弦的相似度计算
基于共同喜欢物品的用户列表计算物品相似度直接使用同时购买这两个物品的人数，但可能存在用户购买了但是不喜欢的情况，所以如果数据集包括具体评分数据，我们可以进一步把用户评分引入相似度计算中
用余弦公式计算任意两本书的相似度，nki是用户k对物品i的评分，如果没有则评分为0
#ItemCF-余弦算法
def ItemSimilarity_cos(train):
C = dict()
N = dict()
for u,items in train.items():
for i in items.keys():
if i not in N.keys():
N[i] = 0
N[i] += items[i]*items[i]
for j in items.keys():
if i==j:
continue
if i not in C.keys():
C[i] = dict()
if j not in C[i].keys():
C[i][j] = 0
#当用户同时购买了i和j,则追加评分乘积
C[i][j] += items[i]*items[j]
W = dict()
for i ,related_items in C.items():
if i not in W.keys():
W[i] = dict()
for j ,cij in related_items.items():
W[i][j] = cij/(math.sqrt(N[i]*math.sqrt(N[j]))
return W
if __name__ =='___main__':
Train_Data = {'A':{'i1':1,'i2':1,'i4':1},
'B':{'i1':1,'i4':1},
'C':{'i1':1,'i2':1,'i5':1},
'D':{'i2':1,'i3':1},
'E':{'i3':1,'i5':1},
'F':{'i2':1,'i4':1},
}
W = ItemSimilarity_cos(Train_Data)（3）热门物品的惩罚
从相似度计算公式发现，当物品i被更多人购买时，分子中的
和分母中的
都会增长，对于热门物品，分子增长速度远远高于，所以会使物品i和其他很多物品的相似度都偏高，这就是ItemCF中的物品热门问题
推荐过于热门，会使个性化感知下降，所以要对热门物品i进行惩罚，
当
,N(i)越小，惩罚的越厉害，从而使热门物品相关性分数下降
def ItemSimilarity_alpha(train,alpha = 0.3):
C = dict()
N = dict()
for i ,item in train.items():
for i in items.keys():
if i not in N.keys():
N[i] = 0
N[i] += 1
for j in items.keys():
if i ==j:
continue
if i not in C.keys():
C[i] = dict()
if j not in C[i].keys():
C[i][j]=0
C[i][j] += 1
W = dict()#书本对相似分数
for i ,related_items in C.items():
if i not in W.keys():
W[i] = dict()
for j, cij in related_items.items:
W[i][j] = cij/(math.pow(N[i],alpha) * math.pow(N[j],1-alpha))
return W
if __name__ =='___main__':
Train_Data = {'A':{'i1':1,'i2':1,'i4':1},
'B':{'i1':1,'i4':1},
'C':{'i1':1,'i2':1,'i5':1},
'D':{'i2':1,'i3':1},
'E':{'i3':1,'i5':1},
'F':{'i2':1,'i4':1},
}
W = ItemSimilarity_alpha(Train_Data)运行以上代码，得到物品间相似度矩阵，可以观察到i2 因为比较热门，被降权惩罚，与其他的物品相似度显著降低
计算用户u对于物品i的预测分数
得到物品之间的相似度之后，计算用户u对于物品i的预测分数 ：
其中S（j，k）是物品j相似物品的集合，一般来说j的相似物品集合是相似分数最高的k个，参照上面计算得出的相似分数。
是用户对已购买的物品i的评分，如果没有推评分数据，则取1。如果待打分的物品和用户购买过的多个物品相似，则将相似分数相加，相加后的得分越高，则用户购买可能性越大。
比如用户购买过《明朝那些事儿》（评分0.8分）和《品三国》（评分0.6分），而《鱼羊野史》和《明朝那些事儿》相似分是0.2 分，《鱼羊野史》和《品三国》的相似分数是0.1分，则用户在《鱼羊野史》上的分数则为 0.22分(0.8x0.2+0.6x0.1)）。
找出与用户喜欢的物品相似度高的top N个，也就是分数最高的N个作为推荐的候选。
# 结合用户喜好对物品排序
def Recommend(train,user_id,W,K):
rank = dict()
ru = train[user_id]#不同的用户ABCDEF
for i,pi in ru.items():#遍历训练集中物品和评分
tmp = W[i]#相似度矩阵，与物品i相似的物品j
for j,wj in sorted(tmp.items(),key = lambda d : d[i] , reverse =True)[0:K]
if j not in rank.keys():
rank[j] = j
#如果用户已经购买过，则不再推荐
if j in ru:
continue
#待推荐的书本j与用户已购买的书本i相似，则累加上相似分数
rank[j] += pi*wj
return rank
if __name__ =='___main__':
Train_Data = {'A':{'i1':1,'i2':1,'i4':1},
'B':{'i1':1,'i4':1},
'C':{'i1':1,'i2':1,'i5':1},
'D':{'i2':1,'i3':1},
'E':{'i3':1,'i5':1},
'F':{'i2':1,'i4':1},
}
W = ItemSimilarity_alpha(Train_Data)
Recommend(Train_Data,'C',W,3)未定义参数K，即对物品相似物品中topK个物品进行召回，K过大，会召回很多相关性不强的物品，导致准确率下降，过小的K会使召回的物品过少，准确率也不高，所以需要尝试不同的K值对比算法的准确率和召回率，以便选择最佳的K值
基于用户的协同算法
基于用户的协同过滤（User CF）的原理和基于物品的协同过滤类似。不同的是，基于物品的协同过滤的原理是用户U购买了A物品，推荐给用户U和A相似的物品B、C、 D。而基于用户的协同过滤，是先计算用户U与其他的用户的相似度，然后取和U最相似的几个用户，把他们购买过的物品推荐给用户U。
计算用户相似度
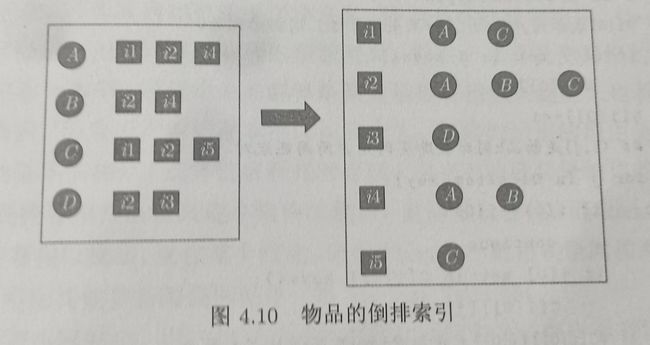
为了计算用户相似度，我们首先要把用户购买过物品的索引数据转化成物品被用户买过的索引数据，即物品的倒排索引。
物品的倒排索引 建立物品倒排索引的参考代码如下：
#建立物品倒排表
def defItemIndex(DictUser):
#defaultdict的作用是在于，当字典里的key不存在但被查找时，返回的不是keyError而是一个默认值defaultdict
DictItem = defaultdict(defaultdict)
#遍历每个用户
for key in DictUser:
#遍历用户k的物品购买记录
for i in DictUser:
DictItem[i[0]][key] = i[1]
return DictItem建立好物品的倒排索引后，就可以根据相似度公式计算用户之间的相似度
N(a) 是购买物品i的用户数，N(b)是购买物品j的用户数，而分子是同时购买物品a和物品b的用户数。
#计算用户相似度
def defUserSimilarity(DictItem):
N = dict()#用户购买的数量
C = defaultdict()#用户同时购买的数量
W = defaultdict()#相似度
#遍历每个物品
for key in DictItem:
#遍历用户K买过的书
for i in DictItem[key]:
# i[0]表示用户的id,如果未计算过，则初始化为0
if i[0] not in N.keys():
N[i[0]] = 0
N[i[0]] += 1
#(i,j)是物品k同时被购买的用户两两相匹配
for j in DictItem[key]:
if i(0) ==j(0):
continue
if j(0) not in C[i[0]].keys():
C[i[0]][j[0]] = 0
# C[i[0]][j[0]]表示用户i和j购买同样书的数量
C[i[0]][j[0]] += 1
for i,related_user in C.items():
for j ,cij in related_user.items():
W[i][j] = cij/math.sqrt(N[i] * N[j])
return W
计算得分
有了用户的相似数据，针对用户U挑选K个最相似的用户，把他们购买过的物品中，U未购买过的物品推荐给用户U即可。如果有评分数据，可以针对这些物品进一步打分，打分的原理与基于物品的推荐原理类似，公式如下：
其中是N（i）物品i被购买的用户集合，S(u,k)是用户u的相似用户集合，挑选最相似的用户k个，将重合的用户v在物品i上的得分乘以用户u和v的相似度，累加后得到用户u对于物品i的得分。
基于用户协同和基于物品协同的区别
基于用户的协同过滤（UserCF）和基于物品协同（ItemCF）在算法上十分类似，推荐系统选择哪种算法，主要取决于推荐系统的考量指标。
1）从推荐的场景考虑。
ItemCF 是利用物品间的相似性来推荐的，所以假如用户的数量远远超过物品的数量，那么可以考虑使用ItemCF，比如购物网站，因其物品的数据相对稳定，因此计算物品的相似度时不但计算量较小，而且不必频繁更新；UserCF更适合做新闻、博客或者微内容的推荐系统，因为其内容更新频率非常高，特别是在社交网络中，UserCF是一个更好的选择，可以增加用户对推荐解释的信服程度。而在一个非社交网络的网站中，比如给某个用户推荐一本书，系统给出的解释是某某和你有相似兴趣的人也看了这本书，这很难让用户信服，因为用户可能根本不认识那个人；但假如给出的理由是因为这本书和你以前看过的某本书相似，这样的解释相对合理，用户可能就会采纳你的推荐。
UserCF是推荐用户所在兴趣小组中的热点，更注重社会化，而ItemCF则是根据用户历史行为推荐相似物品，更注重个性化。所以UserCF一般用在新闻类网站中，如Digg，而ItemCF则用在其他非新闻类网站中，如Amazon、hulu等。
因为在新闻类网站中，用户的兴趣爱好往往比较粗粒度，很少会有用户说只看某个话题的新闻，而且往往某个话题也不是每天都会有新闻。个性化新闻推荐更强调新闻热点，热门程度和时效性是个性化新闻推荐的重点，个性化是补充，所以 UserCF给用户推荐和他有相同兴趣爱好的人关注的新闻，这样在保证了热点和时效性的同时，兼顾了个 性化。另外一个原因是从技术上考虑的，作为一种物品，新闻的更新非常快，随时会有新的新闻出现，如果使用ItemCF的话，需要维护一张物品之间相似度的表，实际工业界这张表一般是一天一更新，这在新闻领域是万万不能接受的。
但是，在图书、电子商务和电影网站等领域，ItemCF则能更好地发挥作用。因为在这些网站中，用户的兴趣爱好一般是比较固定的，而且相比于新闻网站更加细腻。在这些网站中，个性化推荐一般是给用户推荐他自己领域的相关物品。另外，这些网站的物品数量更新速度不快，相似度表一天一次更新可以接受。而且在这些网站中，用户数量往往远远大于物品数量，从存储的角度来讲，UserCF 需要消耗更大的空间复杂度，另外，ItemCF可以方便地提供推荐理由，增加用户对推荐系统的信任度，所以更适合这些网站。
（2）在系统的多样性（也被称为覆盖率，指一个推荐系统能否给用户提供多种选择）指标下，ItemCF的多样性要远远好于 UserCF，因为UserCF 会更倾向于推荐热门的物品。也就是说，ItemCF的推荐有很好的新颖性，容易发现并推荐长尾里的物品。所以大多数情况，ItemCF的精度稍微小于UserCF，但是如果考虑多样性，UserCF 却比ItemCF 要好很多。
由于UserCF 经常推荐热门物品，所以它在推荐长尾里的项目方面的能力不足；而ItemCF 只推荐A领域给用户，这样它有限的推荐列表中就可能包含了一定数量的非热门的长尾物品。ItemCF的推荐对单个用户而言，显然多样性不足，但是对整个系统而言，因为不同的用户的主要兴趣点不同，所以系统的覆盖率会比较好。
（3）用户特点对推荐算法影响的比较。对于UserCF，推荐的原则是假设用户会喜欢那些和他有相同喜好的用户喜欢的东西，但是假如用户暂时找不到兴趣相投的邻居，那么UserCF的推荐效果就会大打折扣，因此用户是否适应UserCF算法跟他有多少邻居是成正比关系的。基于物品的协同过滤算法也是有一定前提的，即用户喜欢和他以前购买过的物品相同类型的物品，那么我们可以计算一个用户喜欢的物品的自相似度。一个用户喜欢物品的自相似度大，就说明他喜欢的东西都是比较相似的，即这个用户比较待合ItemCF方法的基本假设，那么他对ItemCF的适应度自然比较好；反之，如果自相似度小，就说明这个用户的喜好习惯并不满足 ItemCF方法的基本假设，那么用ItemCF方法所做出的推荐对于这种用户来说，其推荐效果可能不是很好。