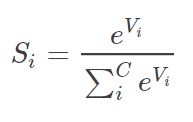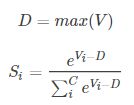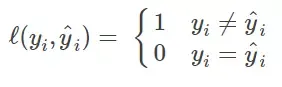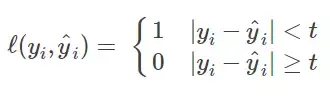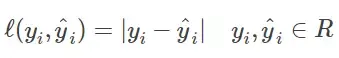机器学习/深度学习入门：损失函数
分类问题损失函数——交叉熵（crossentropy）和Softmax
交叉熵
交叉熵刻画了两个概率分布之间的距离，是分类问题中使用广泛的损失函数。给定两个概率分布p和q，交叉熵刻画的是两个概率分布之间的距离：
对于交叉熵理解比较透彻：https://blog.csdn.net/tsyccnh/article/details/79163834
Softmax
关于Softmax 函数（一般在神经网络中， softmax可以作为(多)分类任务的输出层）的定义如下所示：
实际应用中，使用 Softmax 需要注意数值溢出的问题。因为有指数运算，如果 V 数值很大，经过指数运算后的数值往往可能有溢出的可能。所以，需要对 V 进行一些数值处理：即 V 中的每个元素减去 V 中的最大值。
对于softmax理解比较透彻：https://blog.csdn.net/M_Z_G_Y/article/details/90175421
回归问题损失函数——均方误差（MSE，mean squared error）
均方误差亦可用于分类问题的损失函数，其定义为：
其中yiyi为一个batch中第i个数据的正确答案，而yi′yi′为神经网络给出的预测值。
如下代码展示了如何通过TensorFlow实现均方误差损失函数：
mse = tf.reduce_sum(tf.square(y_ - y))其中y代表了神经网络的输出答案，y_代表了标准答案。
机器学习中的损失函数
一般来说，我们在进行机器学习任务时，使用的每一个算法都有一个目标函数，算法便是对这个目标函数进行优化，特别是在分类或者回归任务中，便是使用损失函数（Loss Function）作为其目标函数，又称为代价函数(Cost Function)。损失函数是用来评价模型的预测值 Y_hat=f(X) 与真实值Y的不一致程度，它是一个非负实值函数。通常使用 L(Y,f(x))来表示损失函数，损失函数越小，模型的性能就越好。
设总有N个样本的样本集为(X,Y)=(
)，
∈[1,N]为样本i的真实值，
=f(xi)，i∈[1,N] 为样本i的预测值，f 为分类或者回归函数。 那么总的损失函数为：
常见的损失函数 L(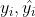
) 有以下几种：
1. 铰链损失（Hinge Loss）：主要用于支持向量机（SVM） 的最大距离，常用于分类算法；
2. 互熵损失 （Cross Entropy Loss，Softmax Loss ）：用于Logistic 回归与Softmax 分类中，常用于分类算法；
3. 平方损失（Square Loss）：主要是最小二乘法（OLS）中；
4. 指数损失（Exponential Loss） ：主要用于Adaboost 集成学习算法中；
5. 其他损失（如0-1损失，绝对值损失，感知损失等）
Zero-one Loss
Zero-one Loss即0-1损失，它是一种较为简单的损失函数，如果预测值与目标值不相等，那么为1，否则为0，即：
该损失函数的意义就是，当预测错误时，损失函数值为1，预测正确时，损失函数值为0。该损失函数不考虑预测值和真实值的误差程度，也就是只要预测错误，预测错误差一点和差很多是一样的。可以看出上述的定义太过严格，如果真实值为1，预测值为0.999，那么预测应该正确，但是上述定义显然是判定为预测错误，那么可以进行改进为Perceptron Loss。
Perceptron Loss
Perceptron Loss即为感知损失。即：
其中t是一个超参数阈值，如在PLA(Perceptron Learning Algorithm,感知机算法)中取t=0.5。
Hinge Loss
Hinge损失可以用来解决间隔最大化问题，如在SVM中解决几何间隔最大化问题，其定义如下：
Log Loss
在使用似然函数最大化时，其形式是进行连乘，但是为了便于处理，一般会套上log，这样便可以将连乘转化为求和，由于log函数是单调递增函数，因此不会改变优化结果。因此log类型的损失函数也是一种常见的损失函数，如在LR(Logistic Regression, 逻辑回归)中使用交叉熵(Cross Entropy)作为其损失函数。即：
规定：
对数损失和交叉熵损失的一点点区别：https://blog.csdn.net/JustKian/article/details/83117170
Square Loss
Square Loss即平方误差，常用于回归中。即：
Absolute Loss
Absolute Loss即绝对值误差，常用于回归中。即：
Exponential Loss
Exponential Loss为指数误差，常用于boosting算法中，如AdaBoost。即：
各损失函数图形
