学习笔记-推荐系统(Recommender systems)
推荐系统在现实中的应用很广:购物网站会根据顾客的购物历史给顾客推荐商品;电影网站也会根据你对一些电影的评分为你推荐新的电影。学完这一章后,发现这背后的逻辑还是挺简单的。
基本假设:用户对某电影的评分由该电影的内容属性组合(X)和用户对这些内容属性的喜好程度(Theta)所决定。
1. Content based recommendations
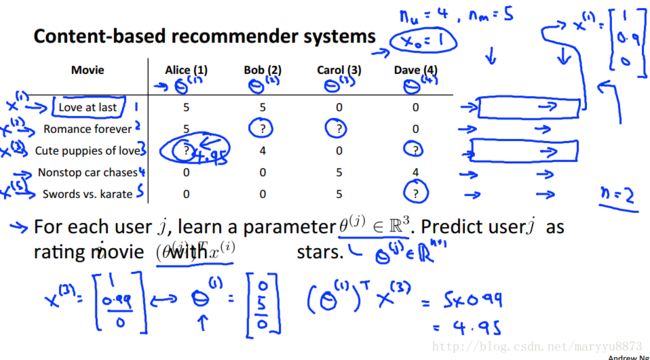
所谓Content based,即已知每部电影的内容属性,包括浪漫、暴力、搞笑等;
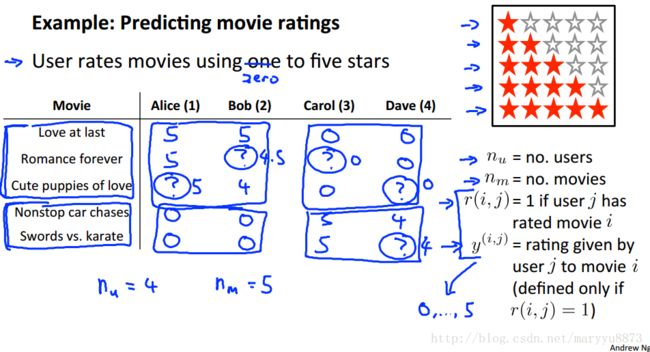
任务:已知每部电影的内容属性,并且已知用户对一些电影的评分,需要预测用户对其它电影的评分。
问题剖析

该类任务(Content_based)其实已经演变成预测用户对每一种内容属性的喜好程度(评分由内容属性和喜好程度决定)。
上述问题的求解思路:通过观察用户对某些电影已有的评分值,预测用户对内容属性的喜好程度。
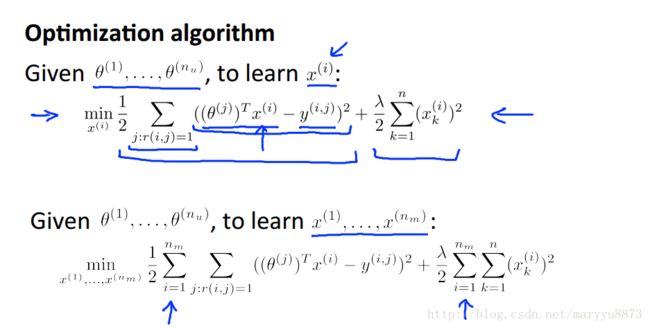
将上述问题公式化如下:

该公式的目的:寻找合适的Theta值,使预测评分与实际评分直接的差异最小化。该公式与我们之前学过的线性回归公式十分相像。
2. Collaborative filtering
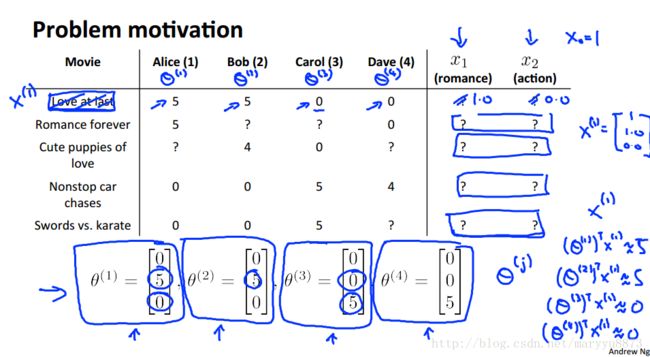
刚才讨论的Content based recommendations是基于已知电影的内容属性(X)组成的前提;
同样的,如果已知用户对内容属性的喜好,并且已知用户对某些电影的评分,就可以预测用户对新电影的评分。
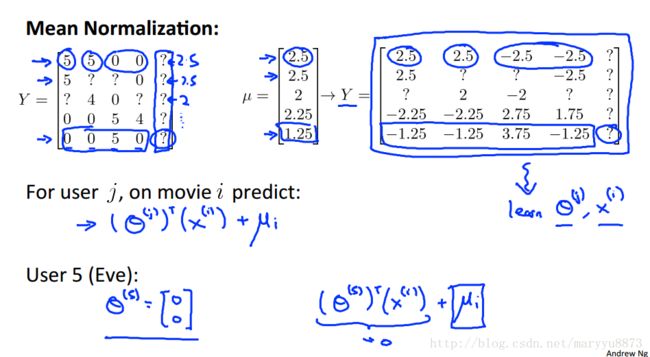
此问题也已演变成,已有用户对某些电影的评分,和用户对内容属性的喜好程度,预测电影的内容属性组合。
Collaborative filtering
通过上面的学习,我们发现,如果已知电影的内容属性和评分,就能够预测用户对内容属性的喜好程度;如果已知用户对内容属性的喜好程度和评分,就能够预测电影的内容属性;上述两部可以进入一个相互迭代的循环过程,使得模型的预测性能不断提高。
Collaborative filtering algorithm
协作过滤算法公式:
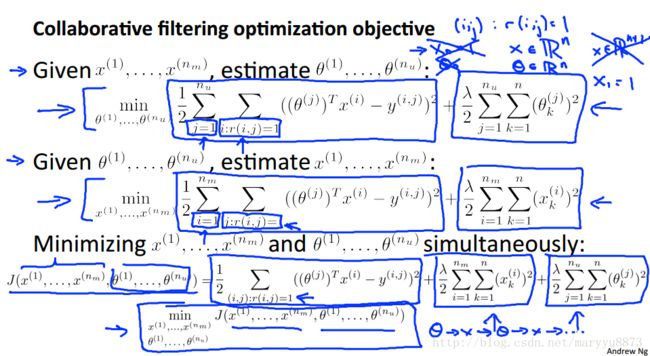
协作过滤算法实现了仅仅已知用户对某些电影的评分,可以同时预测电影的内容属性和用户对这些内容属性的喜好程度,也就是实现了预测用户的新电影的评分。

具体过程:
1. 初始化X和Theta值;
2. 采用梯度下降算法最小化损失函数;
3. 根据Theta和X预测评分。
作业代码:
体验:作业的前半部分,很容易就实现了。但是在Collaborative filtering gradient那一块卡了我好长时间,为此我还把整章的视频全都重新认真地学了一遍,然而实现了之后发现还是挺简单的。
损失函数的公式如下:
J =0.5 * sum(sum(((X*Theta' - Y).^2).*R)) + 0.5*lambda*sum(sum(Theta.^2)) + 0.5*lambda*sum(sum(X.^2));X的导数公式(矩阵化):
X_grad= ((X*Theta' - Y).*R) * Theta + lambda*X;X的导数公式(非矩阵形式):
for i = 1:size(X,1)
idx = find(R(i, :)==1);
Theta_temp=Theta(idx,:);
Y_temp=Y(i,idx);
X_grad(i, :)=(X(i,:)*Theta_temp' -Y_temp)*Theta_temp +lambda*X(i,:);
endTheta的导数(矩阵化):
Theta_grad=((X*Theta' -Y).*R)'*X +lambda*Theta;Theta的导数(非矩阵形式):
for j = 1:size(Theta,1)
idx= find(R(:,j)==1);
X_temp=X(idx,:);
Y_temp=Y(idx,j);
Theta_grad(j,:)=(X_temp*Theta(j,:)' -Y_temp)'*X_temp + lambda*Theta(j,:);
endfor循环理解:(之前死活无法理解Theta的for循环怎么构成)对于每一位用户;找到该用户评分的电影(idx);获取这些评分电影的内容属性;获取这些评分电影的评分值;该用户的对内容属性喜好的梯度:内容属性乘以属性喜好的转置减去实际评分,上部结构的转置再乘以内容属性。
注:如无特殊说明,以上所有图片均截选自吴恩达在Coursera开设的机器学习课程的课件ppt.