matlab符号系统

matlab解决问题的最基本思路是建立脚本文件，那么脚本文件的第一段就是定义一些变量，这和C语言等编程思想是一样的。matlab提供的变量类型很多，最基础的是三种：数值变量、符号变量、字符串，其他的类型还有cell、table等。这里仅说明最基础的变量类型。
其实matlab现在仍然在发展，有越来越多的新的工具箱出现，比如：神经网络，微分方程，深度学习，simulink，以及一些特定的工程文件(不同专业不同需求，matlab受众面很广)等等，所以的话也会有一些特定的数据类型，或者基础上的一些专用变量以及编程方式。

1.数值变量
matlab中所有的数值变量都是矩阵，赋值时，以方括号作为开头和结尾，以英文逗号或空格分割同行元素，以英文分号分割各列。例如在Command Window里输入a=[1 2;3 4]

可以看到运算结果，a是一个数值变量。同时workspace里出现一个田字形的变量a，说明变量a的类型是数值型。

向量和数字可以视为特殊的矩阵，例如

a=[1 2]

a=[1;2]

分别是行向量和列向量。

a=[1] 可以简写为a=1 是数字。
数值变量的命名要求是英文字母开头，不能包含特殊符号，大小写敏感。这里推荐采用下划线来进行分割，例如value_of_A，这和其他编程语言的命名规则大体相当。
赋值中，有时需要用到等差数列，例如定义一个向量a=[1 2 3]，如果比较长，赋值很麻烦，所以matlab提供了一个简单的方法

a=[1:1:3]

这里两个冒号的意思是起始值:步长:终值。采用这种赋值方式时可以获得一个等差数列行向量，并可以省略两侧的方括号。当步长为1时，可以省略步长和一个冒号，于是可以简写为

a=1:3

另一种灵活的赋值方法是分块矩阵，其方法是变量名后面加圆括号，圆括号中加序号。例如

a=[1 2;3 4]

定义变量a之后，

b=a(1,2)

就可以把a的第一行第二列元素赋值给b，当然也可以用

a(1,2)=1

来修改矩阵中部分元素的值。这里需要注意，序号必须是自然数，且不能是零。当矩阵中有多个元素需要赋值时，可以将序号部分改成向量，例如

a([1 2],[1 2])=[1 2;3 4]

中把行数和列数都用向量表示，就是说对矩阵a的第1和2行，第1和2列，总共4个元素赋值。更进一步，也可以有a([1 2],1)表示a的第一列，也可以写成
a(1:end,1)

这里的end表示终点，即a的行数2，也可以更进一步简写成

a(:,1)

这里的冒号表示从头至尾。这类赋值方法最为常用，但基本的语法非常简单，方括号表示矩阵开头和结尾，圆括号表示从矩阵中选取部分，把握这个原则，有利于读懂程序。
当然分块矩阵也可以

b=[a a]

这样的赋值方法，但需要注意的是，方括号中的元素必须满足矩阵的行列数要求，例如

a=[1 1]

b=[1;1]

c=[a b]

就会引起错误，因为此时matlab无法确定c的行列数。
2.符号变量
总体而言，符号变量比数值变量简单得多，因为变化非常少，常用的赋值命令是

syms a b

syms表示这里要定义一些符号变量，a和b是变量名，符号变量的命名规则和数值变量一样。有时候也采用

syms a real

来强调a是实数变量，具体可以doc syms来获得帮助。
有些变量之间存在依赖关系，此时可以定义

syms x y(x)

这里声明x是一个符号变量，又声明y是一个符号变量，且y的值由x决定，这相当于数学中函数的概念。当然具体的函数关系并没有明确规定。也可以

syms x y z(x,y)

来定义符号变量z，z依赖x和y。这相当于二元函数的概念。这里的圆括号显然和数值变量中的圆括号含义完全不同，这也是学习matlab最不习惯的地方，同一个符号，由于变量类型不同会有完全不同的含义。所以在学习matlab的过程中，一定要区分数值变量和符号变量。
上述方法定义的符号变量是一个数，或者1*1矩阵，matlab中也可以定义符号矩阵，例如

syms a11 a12 a21 a22

A=[a11 a12;a21 a22]

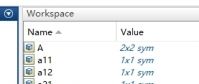
就可以获得一个矩阵符号变量A。
定义符号变量后，workspace中出现相应的变量名，图形不是数值变量的田字形，而是方框里有个立方体，双击后可以看到行列数。

3.字符串

很多编程语言都把字符串当做单独的一种数据类型，毕竟字符这种东西(包括数字，也可以成为字符)，在计算机里面都是需要以数值表示(存储与运算)的，区别于能直接使用数值变量等数据类型，其实函数，类(也就是你的代码块)本身也是字符，但是在计算机中也会帮你转化成特定位置的特定数值(二进制)，所以c语言就有了数据(变量)栈区，堆区(动态，静态，常量，变量等)，程序文件存储(执行操作与跳转，本身也会变成数据，程序数据)区，它的数值代表的含义可能就与普通的变量有所不同，所以数据变量(普通各种基本数据(各种精度))，以及字符串类型。虽然这些编程语言自动帮我们完成了，我们往往不用操心，直接使用即可。

比数值、符号更为简单的就是字符串了，其定义方法是以单引号开头和结尾，例如

a=‘hello world’

就定义了一个字符串a，其值为你好世界。matlab中较为特殊的是，字符串可视为行向量，例如

b='hello ’
c=‘world’
a=[b c]
也可以获得字符串a，其值为你好世界。另外，有时也可以将字符串视为矩阵，例如

a=[‘ab’;‘cd’]

但这种用法很罕见，同时要求各行字符串长度一样，否则将违反矩阵行列数规定。
当然字符串的值也可以是特殊符号，比如

',
就定义了逗号，而最特殊的就是定义单引号，因为单引号会和字符串定义中的单引号混淆，因此matlab中用两个单引号表示一个单引号，也就是

a=’’’’

表示a是一个字符变量，值是一个单引号。语句中第一和第四个单引号是字符串类型的开头和结尾，中间两个单引号用来表示一个单引号。
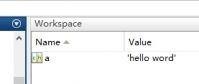
定义字符串变量后，workspace中出现相应的变量名，图像是方框里写了ch，双击后可以看到行列数。

以上参考：https://blog.csdn.net/weixin_42717711/article/details/82620634

---

下面主要详细讲一下符号变量，这个是其他编程语言不太常见的。。
Matlab如何定义符号变量？
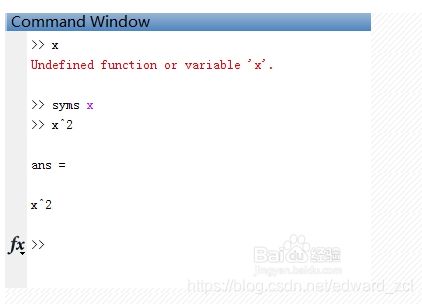
如下面的例子，未定义就会出错。符号变量定义方法例如: sym x 或者 syms x ，两者有区别也有共同点。

其他变量的定义：

计算过程当中的存储数值的变量

可以不必定义，随时需要，随时定义，但是有时候如果变量很多，那么最好提前声明，声明的时候，可以直接赋予0值，并且注释，这样方便以后区分，避免混淆。

矩阵和向量

对于矩阵一般都是需要定义的，定义好矩阵之后，才方便访问/修改矩阵的指定元素，矩阵声明（定义）的方法，常用的 就是声明为零矩阵zeros(M,N),或者单位矩阵ones(M,N),eye(M,N)等。
　　
具体使用因情况而定，比如：Matlab中提供了符号傅里叶变化函数不过使用前 符号变量一定要定义或者转换，否则Matlab不认的

具体如下：

1、简介

编程是编写程序的中文简称，就是让计算机代为解决某个问题，对某个计算体系规定一定的运算方式，是计算体系按照该计算方式运行，并最终得到相应结果的过程。

为了使计算机能够理解人的意图，人类就必须将需解决的问题的思路、方法和手段通过计算机能够理解的形式告诉计算机，使得计算机能够根据人的指令一步一步去工作，完成某种特定的任务。这种人和计算体系之间交流的过程就是编程。

2、汇编程序

汇编程序。使用汇编语言编写计算机程序，程序员仍然需要十分熟悉计算机系统的硬件结构，所以从程序设计本身上来看仍然是低效率的、繁琐的。但正是由于汇编语言与计算机硬件系统关系密切，在某些特定的场合，如对时空效率要求很高的系统核心程序以及实时控制程序等，迄今为止汇编语言仍然是十分有效的程序设计工具。

3、执行原理

计算机对除机器语言以外的源程序不能直接识别、理解和执行，都必须通过某种方式转换为计算机能够直接执行的。这种将高级编程硬件程序设计语言编写的源程序转换到机器目标程序的方式有两种:解释方式和编译方式。

---

matlab里用syms定义的符号和普通的变量有什么区别？
用sym定义的是符号类型变量，和普通的数值类型相比，主要有以下几个方面的区别（个人理解的基础上总结，不一定全面，也不一定正确，仅供参考）：
1、完全没有舍入误差，可以借助于vpa实现高精度运算；
2、可用于公式推导，例如微分、积分、解方程等；
3、不属于MATLAB基本系统，需要符号数学工具箱的支持；
4、很多功能在各版本的兼容性是需要注意的问题，尤其是2008a之前用的Maple内核，2008b之后是MuPad内核，有不少差别。

---

Matlab如何给符号变量赋值？

答：可以用：subs(符号变量/符号变量的矩阵)

syms z1 z2 z3 z4 z11 z22 z33 z44 IL1 IL2 Us1 Us2
A=[1,-1,0,0,0,0,0,0;
0,1,1,0,0,0,0,0;
0,0,0,0,1,-1,0,0;
0,0,0,0,0,1,1,0;
1,0,0,1,1,0,0,1;
z1,z2,-z3,-z4,0,0,0,0;
0,0,0,0,z11,z22,-z33,-z44;
0,0,0,-z4,0,0,0,z44];
B=inv(A);
C=[IL1;IL2;-IL1;-IL2;0;0;0;Us2-Us1];
D=B*C;
z1=1;z2=2;z3=3;z4=4;z11=5;z22=6;z33=7;z44=8;IL1=9;IL2=10;Us1=1;Us2=2;
E1=D(1)+D(5);
E2=D(3)++D(7);
subs(E1)%可以用subs(函数给符号变量赋值)
subs(E2)

---

matlab的符号变量sym，syms

sym与syms

区别1：如果定义变量x，syms x；当用sym生成多个符号变量时,MATLAB要报错

syms函数的功能比sym函数更为强大,它可以一次创建任意多个符号变量.而且,syms函数的使用格式也很简单,使用格式如下:

syms var1 var2 var3…

如:

syms x y z

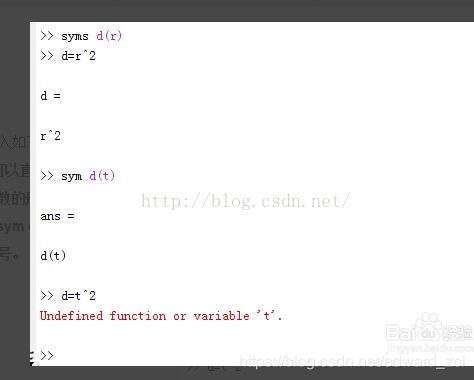
区别2：

syms可以直接声明符号函数d®，并且可以对函数的形式进行赋值改变，但是sym却不可以sym d(t)，只是将d(t)生成了一个整体的符号。

PI = sym(pi);

R = sym(5);

areas = PI * R ^ 2

areas = 25*pi

class(areas)

ans =sym

sym(1/3)

ans =1/3

sym(sqrt(5))

ans =5^(1/2)

sym(sqrt(5) + 1)

ans =910872158600853/281474976710656

sym(1)/sym(3) + sym(1)

ans =4/3

这种符号系统往往有特定的用途，比如Matlab符号求解微分方程等
求解步骤：
（1）先定义符号变量
（2）列出来方程组
（3）替换下式中的量

syms a b c d e vm r Y Nm;
%  Y = a*vm + b*e + c*r ;
%  Nm = d*r + c*( vm+e );
[vm,r] = solve('Y = a*vm + b*e + c*r ','Nm = d*r + c*( vm+e )','vm','r')

备忘一下

参考文献：https://blog.csdn.net/winycg/article/details/52475054