二叉树的建立和遍历
目录
- 创建二叉树中的引用
- 使用遍历顺序创建二叉树
-
- 使用先序遍历和中序遍历创建二叉树
- 使用中序和后序创建二叉树
- 中序求二叉树
- 用栈实现非递归遍历
-
- ==先序遍历==
- ==中序遍历==
- 后序遍历
- 用栈通过出栈次数进行遍历
-
- 中序遍历
- ==后序遍历==
- 队列进行层次遍历
-
- 思路
- 代码
- 判断是否是满二叉树和完全二叉树
-
- 递归
- 非递归
-
- 满二叉树
- 判断完全二叉树
创建二叉树中的引用
在二叉树的存储中,我们发现在创建二叉树函数的时候,,它的参数是char* &str,此处的&是c++中的引用,什么是引用呢?
格式为:类型 &引用变量名 = 已定义过的变量名。
例如:int a=20;int &b=a;,此处的引用b便是a的重命名,怎么理解呢,其实a,b指的是同一个变量,a,b只是他不同的名字。
此处为什么用引用呢,如果去掉引用会发生什么呢?
在数组元素等于ABC##DE##F##G#H## 的时候,输出值会发生错误,发现只在abc之间,不会遍历到后面的元素。怎么样的思路呢,我们递归调用函数时,比如A结点接下来进入左孩子调用函数之后,其在本身函数内也只自增了一次,右孩子调用函数自增一次,在调用的函数时没有在本质上对其进行增加。所以只会输出到abc。要想使其在调用函数时使其数组进行自增,就用到了引用的概念,

用了引用有什么不同呢,创建二叉树函数中用了引用,那么在其函数中的str指的便是主函数中str的别名,str自增一次,其数组本身也就会自增一次,函数调用便会对str影响,没有用引用,函数调用完成之后,返回到原函数时str仍然在原位置,没有进行自增。
使用遍历顺序创建二叉树
使用先序遍历和中序遍历创建二叉树
思路:
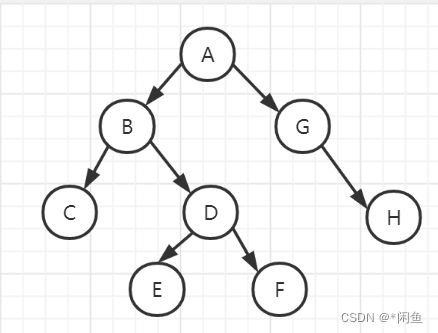
例如:先序:ABCDEFGH ,中序:CBEDFAGH,线序遍历第一个元素是根节点,用根节点将中序遍历的顺序分成两部分CBEDF和GH,分别是左孩子和右孩子。然后将线序去掉根节点,分成BCDEF和GH,第一个结点为左孩子的根节点B,右孩子根节点是G,,将CBEDF由B分成两份,分别是C和EDF,将右孩子划分,根节点是G,在中序遍历中H在G的右边所以是右孩子。剩下就是左孩子一部分,通过这种放法依次进行分类下去,最终就可以将二叉树创建完成。如下图
代码:
int FindPos(const char* istr, int n,const char ch) {
int pos = -1;
for (int i = 0; i < n; ++i) {
if (ch == istr[i]) {
pos = i;
break;
}
}
return pos;
}
BtNode* CreatBTreePI(const char* pstr, const char* istr,int n) {
BtNode* s = nullptr;
if (n > 0) {
s = Buynode();
s->data = pstr[0];
int pos = FindPos(istr, n, pstr[0]);
if (-1 == pos) exit(1);
s->leftchild = CreatBTreePI(pstr+1,istr,pos);
s->rightchild = CreatBTreePI(pstr+pos+1,istr+pos+1,n-pos-1);
}
return s;
}
BtNode* CreateBinaryTreePI(const char* pstr, const char* istr) {
int n = strlen(pstr);
int m = strlen(istr);
if (nullptr == pstr || nullptr == istr || n < 1 || m < 1 || n != m) return nullptr;
else return CreatBTreePI(pstr, istr, n);
}
使用中序和后序创建二叉树
思路此处不做过多展示,同线序和中序一样,只是根节点先序在第一个,后序在最后一个。直接给出代码:
int FindPos(const char* istr, int n,const char ch) {
int pos = -1;
for (int i = 0; i < n; ++i) {
if (ch == istr[i]) {
pos = i;
break;
}
}
return pos;
}
BtNode* CreatBTreeIL(const char* istr, const char* lstr, int n) {
BtNode* s = nullptr;
if (n > 0) {
s = Buynode();
s->data = lstr[n-1];
int pos = FindPos(istr, n, lstr[n-1]);
if (-1 == pos) exit(1);
s->leftchild = CreatBTreeIL(istr , lstr, pos);
s->rightchild = CreatBTreeIL(istr + pos + 1, lstr + pos, n - pos - 1);
}
return s;
}
BtNode* CreateBinaryTreeIL(const char* istr, const char* lstr) {
int n = strlen(istr);
int m = strlen(lstr);
if (nullptr == lstr || nullptr == istr || n < 1 || m < 1 || n != m) return nullptr;
else return CreatBTreeIL(istr, lstr, n);
}
中序求二叉树
给出如下图这样一个由树先序遍历得到的数组,能否求出该树的中序遍历。
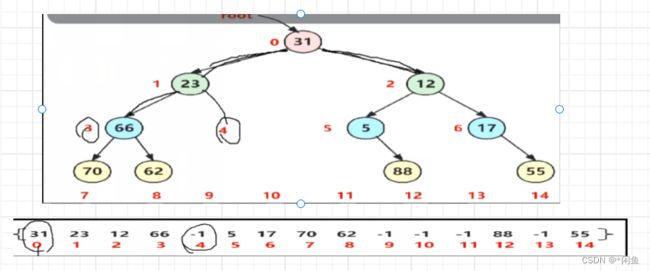
我们可以看出树中为空的位置都用-1替换了,我们可以想想办法用他的编号和高度来求其元素。代码中左孩子和右孩子的编号分别是双亲节点编号的二倍+1和+2。
代码:
BtNode* InOrder_Ar(int *arr,int i,int n){
if(i<n&&arr[i]!=-1){
InOrder_Ar(arr,i*2+1,n);//life
printf("%5d",arr[i]);
InOrder_Ar(arr,i*2+1,n);//right
}
}
int main(){
int arr[]={31,23,12,66,-1,5,17,70,62,-1,-1,-1,88,-1,55};
int n=sizeof(arr)/sizeof(arr[0]);
InOrder_Ar(arr,0,n);
}
用栈实现非递归遍历

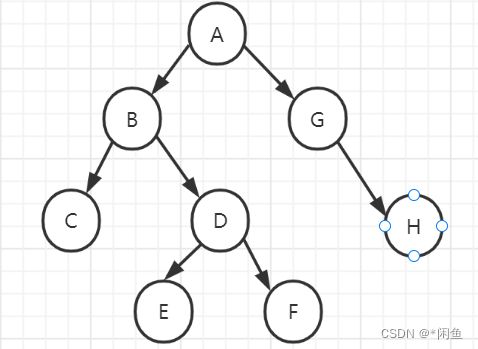
给出如图的二叉树,如何不使用递归来遍历二叉树呢,我们用需要用栈进行辅助。
先序遍历
思路:先序遍历我们会发现规律都是先输出最左孩子,然后从左孩子的最后一个结点的右兄弟开始遍历,依次向根节点遍历。因为是栈,尾插尾删,所以我们从根节点的右孩子开始依次将右孩子入栈,直到左孩子为null,然后从栈顶(最后一个)元素依次遍历。
void NicePreOrder(BtNode* ptr) {
if (nullptr == ptr) return;
stack<BtNode*>st;
while (ptr != nullptr || !st.empty()) {
while (ptr != nullptr) {
printf("%c ", ptr->data);
if (ptr->rightchild != nullptr) {
st.push(ptr->rightchild);
}
ptr = ptr->leftchild;
}
if (!st.empty()) {
ptr = st.top(); st.pop();
}
}
/*
if (nullptr == ptr) return;
stack st;
st.push(ptr);
while (!st.empty())
{
ptr = st.top(); st.pop();
printf("%3c", ptr->data);
if (ptr->rightchild != nullptr)
{
st.push(ptr->rightchild);
}
if (ptr->leftchild != nullptr)
{
st.push(ptr->leftchild);
}
}
printf("\n");
*/
}
中序遍历
思路:因为中序遍历的顺序是左中右,所以从根节点开始遍历最先输出的应该是最左边的结点,从根节点开始入栈,根节点的左节点一直从根节点往下找左节点,直到左孩子为null停止查找,取出栈顶元素,将其出栈,因为左根右,所以应该输出当前结点的data域,接下来遍历他的右孩子,然后继续循环判断其左孩子依次循环吗,直到栈为null结束循环,因为是while循环,并且刚开始栈为空不能进入循环所以进入循环的条件加上ptr!=null.
void NiceInOrder(BtNoder* ptr){
if(nnullptr==ptr) return;
st::stack<BtNode*>st;
while(ptr!=nullptr||!st.empty()){
while(ptr!=nullptr){
st.push(ptr);
ptr=ptr->leftchild;
}
ptr=st.top();st.pop();
printf("%3c",ptr->data);
ptr=ptr->rigthchild;
}
printf("\n");
}
后序遍历
我们的后序遍历和中序遍历唯一不同的地方是其先判断右孩子,右孩子不存在或者已经输出过了之后才会输出结点的data域,因此我们选择做标记。我们定义一个结点tag,如果结点输出过了,令tag=右孩子,所以我们在输出前加入了条件如果该结点的右孩子等于null或者右孩子等于我们的标记,条件满足就输出。如果不满足我们就将右孩子入栈,然后令ptr=右孩子。结点变为右孩子进入重新遍历
void NicePastOrder(BtNoder* ptr){
if(nnullptr==ptr) return;
st::stack<BtNode*>st;
BtNode* tag=nullptr;
while(ptr!=nullptr||!st.empty()){
while(ptr!=nullptr){
st.push(ptr);
ptr=ptr->leftchild;
}
ptr=st.top();st.pop();
if(ptr->rigthchild==nullptr||ptr->rigthchild==tag){
printf("%3c",ptr->data);
tag=ptr;
ptr=nullptr;
}
else{
st.push(ptr);
ptr=ptr->rigthchild;
}
}
printf("\n");
}
用栈通过出栈次数进行遍历
思路我们以后序遍历为例做一阐述:每次出栈队队其结点的计数器进行+1,我们通过结点的计数器判断其输出到了该结点的哪个元素。首先根结点入栈,计数器为0,取栈顶元素并且出栈,判断计数器+1是否等于3,若等于3则输出,(为什么此处前置++呢,因为出栈依次就需要+1,如果不等于3就是第一次或者第二次出栈,就要再次入栈),判断左节点的计数器是否等于1如果是则进行左节点入栈,判断计数器是否等于2,若是右节点入栈,注意此处必须左右孩子不为null。这样一个结点的计数器等于3时变不需要进行再次入栈,直接输出即可。
因为先序遍历直接输出data域即可,所以用出栈次数没有意义
中序遍历
void NiceInOrder_2(BtNode* ptr) {
if (ptr == nullptr) return;
stack<StkNode>st;
st.push(StkNode{ ptr,0 });
while (!st.empty()) {
StkNode node = st.top(); st.pop();
if (++node.popnum == 2) {
printf("%c ", node.pnode->data);
if (node.pnode->rightchild != nullptr) {
st.push(StkNode{ node.pnode->rightchild,0 });
}
}
else {
st.push(node);
if (node.popnum == 1 && node.pnode->leftchild != nullptr) {
st.push(StkNode{ node.pnode->leftchild ,0 });
}
}
}
}
后序遍历
void NicePastOrder_2(BtNode* ptr) {
if (ptr == nullptr) return;
stack<StkNode>st;
st.push(StkNode{ptr,0});
while (!st.empty()) {
StkNode node = st.top(); st.pop();
if (++node.popnum == 3) {
printf("%c ",node.pnode->data);
}
else {
st.push(node);
if (node.popnum == 1&&node.pnode->leftchild!=nullptr) {
st.push(StkNode{ node.pnode->leftchild ,0});
}
if (node.popnum == 2 && node.pnode->rightchild != nullptr) {
st.push(StkNode{node.pnode->rightchild,0});
}
}
}
}
队列进行层次遍历
思路
如上图:层次遍历的顺序是ABGCDHEF,因为我们用的是队列,先入先出,所以我们的层次遍历是从右孩子向左孩子依次入队,先将根节点入队,接判断其右孩子左孩子是否存在,若存在依次入队,接着继续判断队列是否
队列为null进入循环,取出队首元素并且出队,依次进行判断左右孩子入队循环下去即可。用上图举例,首先a入队,a的左孩子右孩子都存在,所以gb依次入队,取出队首元素并且出队,b判断b的左右孩子dc依次入队,接着依次遍历下去,直到队列为null即可。
代码
void LevelOrder(BtNode* ptr) {
if (ptr == nullptr) return;
queue<BtNode*>qu;
qu.push(ptr);
while (!qu.empty()) {
ptr = qu.front(); qu.pop();
printf("%c ",ptr->data);
if (ptr->rightchild != nullptr) {
qu.push(ptr->liftchild);
}
if (ptr->leftchild != nullptr) {
qu.push(ptr->rightchild);
}
}
printf("\n");
}
判断是否是满二叉树和完全二叉树
递归
利用二叉树的大小和深度关系进行计算比较
int max(int a, int b) {
return a > b ? a : b;
}
int GetSize(BtNode* ptr) {
if (ptr == nullptr)return 0;
else return 1 + GetSize(ptr->leftchild) + GetSize(ptr->rightchild);
}
int GetDepth(BtNode* ptr) {
if (ptr == nullptr) return 0;
else return 1 + max(GetDepth(ptr->leftchild), GetDepth(ptr->rightchild));
}
bool IsFullBTree(BtNode* ptr) {
if (ptr == nullptr) return false;
else return pow(2, GetDepth(ptr))-1 == GetSize(ptr);
}
非递归
满二叉树
思路:如上图,我们用到两个队列,先将1存入a队列,遍历a队列中的元素,同时将a的左右孩子存入b队列,接下来将b队列元素依次遍历将b这一层的元素2,3的孩子都依次入到a栈中去,就这样依次a,b两个队列相互配合,但是判断的条件在哪里呢?因为是完全二叉树所以第一层肯定是一个元素,第二层是1+1=2个元素,第三层是2+2=4个元素,很明显就是1,2,4,8,16这样下去。我们判断出队的循环中如果小于此时那一层的数时,就不是满二叉树,如果那一个的队列因为数据都会null(其下一层没有左右孩子)而队列为null此时就退出循环,返回真,说明是完全二叉树。
bool IsFullBinaryTree(BtNode* ptr) {
bool ret = true;
if (ptr == nullptr) return ret;
queue<BtNode*>qua;
queue<BtNode*>qub;
int n = 1;
qua.push(ptr);
while (!qua.empty() || !qub.empty()) {
int i= 0;
for (; i < n&&!qua.empty(); ++i) {
ptr = qua.front(); qua.pop();
if (ptr->leftchild != nullptr) {
qub.push(ptr->leftchild);
}
if (ptr->rightchild != nullptr) {
qub.push(ptr->rightchild);
}
}
if (i < n) {
ret = false;
break;
}
if (!qub.empty()) break;
n += n;
for (int i = 0; i < n && !qua.empty(); ++i) {
ptr = qub.front(); qub.pop();
if (ptr->leftchild != nullptr) {
qua.push(ptr->leftchild);
}
if (ptr->rightchild != nullptr) {
qua.push(ptr->rightchild);
}
}
if (i < n) {
ret = false;
break;
}
if (!qub.empty()) break;
n += n;
}
return ret;
}
判断完全二叉树
思路:将二叉树从根开始,从左向右依次入队,因为是队列,头删尾插,所以应该从左向右依次入队。入队直到ptr为null,所以队列的退出入队,开始遍历剩下的,因为是完全二叉树,所以最后的一部分不能存在数据,也就是说树中最后的元素都必须为null,否则就是不完全二叉树。
bool IsCompBinaryTree(BtNode* ptr) {
bool ret = true;
queue<BtNode*>qu;
qu.push(ptr);
while (!qu.empty()) {
ptr = qu.front(); qu.pop();
if (ptr->leftchild == nullptr) {
break;
}
qu.push(ptr->leftchild);
qu.push(ptr->rightchild);
}
while (!qu.empty()) {
ptr = qu.front(); qu.pop();
if (ptr == nullptr) {
ret = false;
break;
}
}
return ret;
}