机器学习实战之K近邻法-Python实现

一、算法简介

k近邻法（k-nearest neighbor,k-NN）是一种基本的分类方法，输入的是实例的特征向量，对应于特征空间的点，输出结果为实例的类别，可以取多类。对于训练集来说，每个实例的类别已定，当分类时，对于新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式来进行预测。k近邻法分类过程不具有显式的学习过程，其实际上是利用训练数据集对特征向量空间进行划分，从而作为后面分类的模型。对于k近邻法来说，最重要的是k值的选择、距离的度量以及分类决策规则得确定三个基本要素。

算法输入：

                                                          

其中，为实例的特征向量，为实例的类别，;实力特征向量x;

算法输出：实例x所属的类y.

算法步骤：

1.根据给定的距离度量，在训练集T中找出与x最近邻的k个点，涵盖这k个点的x的邻域记作;

2.在中根据分类决策规则（如多数表决）决定x的类别y：

                                                                                       其中，I为指示函数，即当时I为1，否则I为0.

优点：精度高、对异常值不敏感、无数据输入假定。

缺点：计算复杂度高、空间复杂度高。

适用数据范围：数值型和标称型。

（1）、距离度量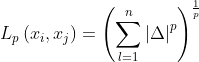：,其中,当p=2时为欧氏距离，当p=1时为曼哈顿距离以及当时，它是各个坐标距离的最大值，即。下图给出了p取不同值时与远点的距离为1的点的图形。

                  

（2）、k值的选择：k值的减小就意味着整体模型变得复杂，容易发生过拟合，通常采用交叉验证法来选取最优的k值。

（3）、分类决策规则：常用的为多数表决。

k近邻法代码如下：（采用欧氏距离和python 3.7）

def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

二、算法示例（摘录自《机器学习实战》，python 3.7）

我的朋友海伦一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的人选，但她没有从中找到喜欢的人。经过一番总结，她发现曾交往过三种类型的人：

           □ 不喜欢的人
           □ 魅力一般的人
           □ 极具魅力的人

尽管发现了上述规律，但海伦依然无法将约会网站推荐的匹配对象归人恰当的分类。她觉得可以在周一到周五约会那些魅力一般的人，而周末则更喜欢与那些极具魅力的人为伴。海伦希望我们的分类软件可以更好地帮助她将匹配对象划分到确切的分类中。此外海伦还收集了一些约会网站未曾记录的数据信息，她认为这些数据更有助于匹配对象的归类。

2.1 准备数据

海伦收集约会数据巳经有了一段时间，她把这些数据存放在文本文件datingTestSet.txt中，每个样本数据占据一行，总共有1000行。海伦的样本主要包含以下3种特征：
□ 每年获得的飞行常客里程数
□ 玩视频游戏所耗时间百分比
□ 每周消费的冰淇淋公升数
在将上述特征数据输人到分类器之前，必须将待处理数据的格式改变为分类器可以接受的格式。创建名为file2matrix的函数，以此来处理输人格式问题。该函数的输人为文件名字符串，输出为训练样本矩阵和类标签向量。代码如下：

def file2matrix(filename):
    fr = open(filename)
    numberOfLines = len(fr.readlines())  # get the number of lines in the file
    returnMat = zeros((numberOfLines, 3))  # prepare matrix to return
    classLabelVector = []  # prepare labels return
    fr = open(filename)
    index = 0
    for line in fr.readlines():
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index, :] = listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1]))
        index += 1
    return returnMat, classLabelVector

从上面的代码可以看到，Python处理文本文件非常容易。首先我们需要知道文本文件包含多少行。打开文件，得到文件的行数。然后创建以零填充的矩阵NumPy(实际上，NumPy是一个二维数组，这里暂时不用考虑其用途)。为了简化处理，我们将该矩阵的另一维度设置为固定值3 , 你可以按照自己的实际需求增加相应的代码以适应变化的输人值。循环处理文件中的每行数据 , 首先使用函数line.strip()截取掉所有的回车字符，然后使用tab字符\t将上一步得到的整行数据分割成一个元素列表。接着，我们选取前3个元素，将它们存储到特征矩阵中。Python语言可以使用索引值-1表示列表中的最后一列元素，利用这种负索引，我们可以很方便地将列表的最后一列存储到向量classLabelVector中。需要注意的是，我们必须明确地通知解释器，告诉它列表中存储的元素值为整型，否则?”如0语言会将这些元素当作字符串处理。以前我们必须自己处理这些变量值类型问题，现在这些细节问题完全可以交给NumPy函数库来处理。

2.2 分析数据：利用Matplotlib创建散点图分析数据的具体情况

2.3 准备数据：归一化处理

在处理这种不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为0到1或者-1到1之间。下面的公式可以将任意取值范围的特征值转化为0到1区间内的值：

def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m, 1))
    normDataSet = normDataSet / tile(ranges, (m, 1))  # element wise divide
    return normDataSet, ranges, minVals

在函数autoNorm中，我们将每列的最小值放在变量minVals中，将最大值放在变量maxVals中 ,其中dataSet.min(0)中的参数0使得函数可以从列中选取最小值，而不是选取当前行的最小值。然后，函数计算可能的取值范围，并创建新的返回矩阵。

为了测试分类器效果，创建函数datingClassTest,

def datingClassTest():
    hoRatio = 0.10  # hold out 10%
    datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')  # load data setfrom file
    normMat, ranges, minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs = int(m * hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
        print('the classifier came back with: {0}, the real answer is:{1}'.format(classifierResult, datingLabels[i]))
        if (classifierResult != datingLabels[i]):
            errorCount += 1.0
    print('the total error rate is:{}'.format(errorCount/float(numTestVecs)))
    print(errorCount)

函数datingClassTest首先使用了file2matrix和autoNorm函数从文件中读取数据并将其转换为归一化特征值。接着计算测试向量的数量，此步决定了normMat向量中哪些数据用于测试，哪些数据用于分类器的训练样本；然后将这两部分数据输人到原始kNN分类器函数classify ()。最后，函数计算错误率并输出结果。

数据和源码：链接：https://pan.baidu.com/s/1rqDZK-xb5y0cFV4knzIpyg 提取码：6br6 （其中还包括手写识别系统的代码和数据以及其他资源）