深度学习常见损失函数总结+Pytroch实现

一、引言

啊啊啊，最近读到一篇论文用到了三元组损失，看的要把人给逼疯了。故在此先总结一下深度学习常见的损失函数以及其Pytroch实现，以方便我以后读论文和看源码。此外，由于现阶段见识浅薄，后面会遇到其它损失函数会接着更新。（小声bb，之前整理过一次，但太过简单了）

二、损失函数

1.均方差损失（Mean Squared Error Loss）

均方差损失（MSE）也称为L2损失，其数学公式如下：
$$J_{MSE}=\frac{1}{N}\sum _{i=1}^N(y_i-y_i^{‘})$$
在模型输出与真实值的误差服从高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一致的。至于啥模型输出与真实值的误差服从高斯分布，这个还真的难说，极大似然估计是概率论中用来近似计算真实分布中的参数的一种方法。

Pytroch官方文档如下：

官方文档介绍：size_average和reduce已经被弃用，reduction可以选择‘mean’和‘sum’，这两者区别在于一个求完和后还要取均值，一个求完和后啥都不干。

实例如下：

	import torch
	import torch.nn as nn 
	
	loss_mean = nn.MSELoss()
	loss_sum = nn.MSELoss(reduction='sum')
	input = torch.randn(3, 5, requires_grad=True)
	target = torch.randn(3, 5)
	output_mean = loss_mean(input, target)
	output_sum = loss_sum(input, target)
	print(output_mean)
	print(output_sum)

2.平均绝对误差损失（Mean Absolute Error Loss）

平均绝对误差损失（MAE）也称为L1 loss，其数学公式如下：
$$J_{MAE}=\frac{1}{N}\sum _{i=1}{}^N|y_i-y_i^{{}^{\prime }}|$$
在模型输出与真实值的误差服从拉普拉斯分布的假设下，最小化平均绝对误差损失与极大似然估计本质是一致的。

Pytroch官方文档如下：

这个用法和上述的MSE一样，这里就不再过多介绍了。

3.交叉熵（Cross Entropy Loss）

（1）信息论中的熵

请注意下述中p指的是真实概率值，q指的是预测概率值。

a.熵

熵的数学公式如下（离散情况下）：
$$H(p)=Entropy=-\sum _{x}p(x)logp(x)$$

b.相对熵（KL散度）

KL散度在讯息系统中称为相对熵，在连续时间序列中称为随机性，在统计模型推断中称为讯息增益，也称讯息散度。

KL散度是两个几率分布P和Q差别的非对称性的度量。KL散度是用来使用基于Q的分布来编码服从P的分布样本所需的额外平均比特数。典型情况下，P表示数据的真实分布，Q表示数据的理论分布。
$$D_{KL}(p||q)=\sum _{x}p(x)log\frac{p(x)}{q(x)}$$
从其概念可以看出KL散度是大于等于0的，数学上利用吉布斯不等式可以证明得到。
$$D_{KL}(P||Q)\ge 0，当且仅当P=Q时等号成立$$
此外，KL散度不是对称函数，因此它不是一个度量或者距离函数。
$$D_{KL}(P||Q)\ne D_{KL}(Q||P)$$

c.交叉熵

在信息论中，基于相同事件测度的两个概率分布p和q的交叉熵是指，当基于一个“非自然”（相对于“真实”分布p而言）的概率q进行编码时，在事件集合中唯一标识一个事件所需要的平均比特数。

给定两个概率分布p和q，p相对于q的交叉熵定义为：
$$H(p,q)=E_p[-logq]=H(p)+D_{KL}(p||q)$$
其中，在离散情况下，交叉熵计算公式如下：
$$H(p,q)=-\sum _{x}p(x)logq(x)$$
$$H(p)=-\sum _{x}p(x)logp(x)$$
$$D_{KL}(p||q)=H(p,q)-H(p)=-\sum _{x}p(x)logq(x)+\sum _{x}p(x)logp(x)=\sum _{x}p(x)log\frac{p(x)}{q(x)}$$
从交叉熵和熵之间上述的数学关系表达式和KL散度非负可以知道当且仅当P=Q时，交叉熵和熵相等，我们可以利用这个来把交叉熵作为损失函数用来使得估计出来的概率值逼近真实值。

（2） 常见的交叉熵函数

a.one-hot编码

我们知道使用神经网络进行预测往往是选择一个特征网络作为Backbone，然后在Backbone后添加一个分类层（常见的有FC+SoftMax），最后输出的结果是类别的概率。比如要区分手写体1，2，3，神经网络输出的结果是【0.3，0.4，0.3】分别表示预测为1的概率为30%、为2的概率为40%、为3的概率为30%，取这三个概率值的最大值作为最终的输出结果即0.4，预测结果为2。

好了，上面啰嗦是因为分类的标签可不是一个向量而只是一个数。这就有一个问题出现了，这该咋计算损失函数呢。这个时候就需要one-hot编码来撑场面了。one-hot编码核心思想是用0、1来进行编码，0表示非，1表示是。上述例子标签如果为2，则对应的one-hot编码为【010】、如果为3则one-hot编码为【001】，也就是one-hot编码把原来的一个数编码成尺寸大小为1*类别数的向量，向量值为0或者1。

b.SoftMax函数和Sigmoid函数

在数学，尤其是概率论和相关领域中，Softmax函数，或称归一化指数函数，是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量中，使得每一个元素的范围都在（0,1）之间，并且所有元素的和为1.
$$F(z{)}_j=\frac{e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}$$
Sigmoid函数表达式如下：
$$y=\frac{1}{1+e^{-x}}$$

c.交叉熵损失函数

这个之前已经介绍过交叉熵了，那么交叉熵损失函数不就出来了。令$y$为真实概率值，$y^{\prime }$为预测概率值，则交叉熵损失函数为：
$$Loss=-\sum _i^{N}ylog{y}^{\prime }，N为类别数$$
特别的当N为2的时候该损失函数为二分类交叉熵损失函数，表达式如下：
$$Loss=-ylog{y}^{\prime }-(1-y)log(1-y^{\prime })$$
函数图像如下：

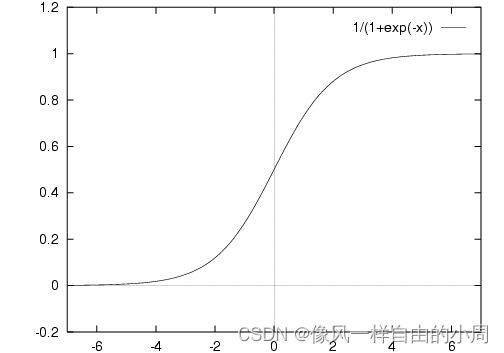
Sigmoid函数是一个常见的激活函数，同时也是一个非线性函数。

（3）Pytroch实现交叉熵损失函数

Pytroch实现交叉熵损失函数的接口有很多，其中有一些输入需要把特征经过Softmax、SigMoid啥的，Label进行one-hot编码，有些不需要。

a.torch.nn.CrossEntropyLoss()

输入特征不需要进行softmax操作，label不需要进行one-hot编码。 该函数结合了LogSoftmax和NLLLoss。

• weight：一个1维张量，给每个类别对应的权重，用来处理样本类别数量不平衡的问题。
• size_average：没有啥用，已经被弃用了。
• ignore_index：指定一个被忽略的目标值，不对输入梯度产生影响。当size_average为True时，损失是对非忽略的目标值进行平均的。
• reduce：没有啥用，已经被弃用了。
• reduction：和MSE的参数一样，一个是均值一个是求和。
• label_smoothing：没用过，也不知道咋用。

	# Example of target with class indices
	loss = nn.CrossEntropyLoss()
	input = torch.randn(3, 5, requires_grad=True)
	target = torch.empty(3, dtype=torch.long).random_(5)
	output = loss(input, target)
	output.backward()
	# Example of target with class probabilities
	input = torch.randn(3, 5, requires_grad=True)
	target = torch.randn(3, 5).softmax(dim=1)
	output = loss(input, target)
	output.backward()

b.torch.nn.NLLLoss

参数的话，和上面的nn.CrossEntropyLoss一样。

该函数就是取出target对应元素的相反数。
比如输入是[[1, 2], [3, 4]]，target是[1, 0]
那么通过该函数后得到结果为-2.5。计算过程为因为target为[1, 0]，所以对应的取输入的第一行的第2个值2，第二行的第1个值3。取相反数相加求均值得(-2 + -3) /2=-2.5。

	import torch
	import torch.nn as nn 
	
	# Example of target with class indices
	loss = nn.NLLLoss()
	input = torch.tensor([[1., 2.], [3., 4.]])
	print(input)
	target = torch.tensor([1, 0])
	print(target)
	output = loss(input, target)
	print(output)

c.torch.nn.BCELoss和torch.nn.BCEWithLogitsLoss

输入特征需要做Sigmoid计算，label需要进行编码。用来进行二分类交叉熵。

	m = nn.Sigmoid()
	loss = nn.BCELoss()
	input = torch.randn(3, requires_grad=True)
	target = torch.empty(3).random_(2)
	output = loss(m(input), target)
	output.backward()

输入特征不需要做Sigmoid计算，label需要进行编码。用来进行二分类交叉熵。

	loss = nn.BCEWithLogitsLoss()
	input = torch.randn(3, requires_grad=True)
	target = torch.empty(3).random_(2)
	output = loss(input, target)
	output.backward()

4.三元组损失

三元组损失就有意思了，三元组损失来自于FaceNet: A Unified Embedding for Face Recognition and Clustering这篇CVPR2015年论文。

这篇论文主要介绍了三元组损失函数的表达式，三元组的挖掘方式，以及一系列实验论证方法的有效性。

Triplet loss本质上是属于度量学习（Metric Learning）的范围，其借鉴了度量学习中的经典大间隔最近邻（Large Margin Nearest Neighbors，LMNN）算法。以Triplet loss为训练准则的深度神经网络模型既兼顾了度量学习的朴素性，又拥有神经网络优秀的非线性建模能力，能够在极大程度上简化并且控制模型训练过程。

• 表达式
  $$L=\sum _i^N[||f(x_i^a)-f(x_i^p)|{|}_2^2-||f(x_i^a)-f(x_i^n)|{|}_2^2+\alpha {]}_{+}$$
  表达式中$x_i^a$表示锚点，$x_i^p$表示和锚点属于同一个类别即正样本，$x_i^n$表示和锚点不属于同一个类别即负样本。举论文中的例子进行说明，进行人脸识别，数据集包含了100个人的人脸照，每个人的人脸照有10张，这样任取一个人的人脸照即$x_i^a$，然后属于同一个人的人脸照的其它9张照片为$x_i^p$，剩下的照片为$x_i^n$。$\alpha$为一个阈值，用来控制正负样本对和锚点之间的距离。

  这个函数的主要思想是为了求得一个embedding（特征映射，简单的理解就是特征提取器，输入$x$得到$f(x)$）。利用这个embedding我们便可以进行度量学习，如用KNN算法求得属于同一个类别的图片啥的。图像配准的HardNet就是采用了这个函数。

  上式要求$x_i^n$到$x_i^a$的距离至少要比$x_i^p$到$x_i^a$的距离大α，显然α越大不同类别之间的可区分性就越强，相应的训练难度也越大。当然也可以把α设为0，这样条件就放的比较宽松了，但是triplet loss的优势也就很难体现出来了。
  
  这里就有个比较有意思的问题：这个$x_i^p$和$x_i^a$可以在相应的正负样本集合里面随便取吗？

  答案显然是不能随便取，举一个极端的例子，如果随便取就有一种情况就是每次取的$x_i^p$和$x_i^a$每次都是一样的，而这个$x_i^p$和$x_i^a$一个相对于$x_i^a$较近，一个相对较远，使得剩下的正样本中可能存在$x_i^{p^{\prime }}$有$||f(x_i^a)-f(x_i^p)|{|}_2^2<||f(x_i^a)-f(x_i^{p^{\prime }})|{|}_2^2$，剩下的负样本中可能存在$x_i^{n^{\prime }}$有$||f(x_i^a)-f(x_i^n)|{|}_2^2>||f(x_i^a)-f(x_i^{n^{\prime }})|{|}_2^2$。易知，这样训练得到的结果是没有每次都取困难样本要好的。

  啥是困难样本呢？满足下述公式的便是:
  $$argma{x}_{x_i^p}||f(x_i^a)-f(x_i^p)|{|}_2^2,argmi{n}_{x_i^n}||f(x_i^a)-f(x_i^n)|{|}_2^2$$

  这就涉及一个问题，这个三元组该咋取，每次运行完都把所有样本的相对距离计算一遍？这个计算量也太顶了吧。作者在论文中提到了两种选取方法，如下：

1.每 n 步离线生成三元组，使用最近的网络检查点并计算数据子集的 argmin 和 argmax。
2.在线生成三元组。这可以通过从小批量中选择硬正/负样本来完成。

论文中作者选择了在打散的整体样本空间随机选择二元组，在batch中选取合适的negative组成三元组，来计算三元组损失。

• 三元组分类
  

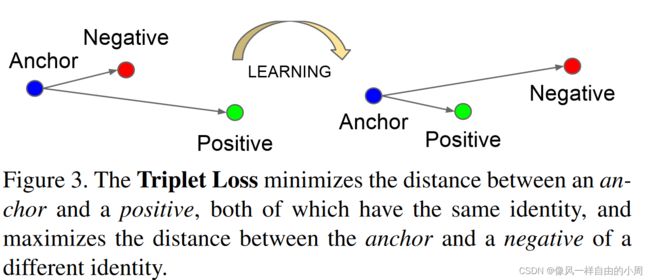
（a）easy triplets（简单三元组）：指在未经过训练的情况下，Triplet loss值已经为0的三元组，此时网络不需要训练学习就满足损失函数的要求。
$$||f(x_i^a)-f(x_i^p)|{|}_2^2+\alpha <||f(x_i^a)-f(x_i^n)|{|}_2^2$$
（b）semi-hard triplets（一般三元组）：指负样本与基准样本间的距离大于正样本与基准样本间的距离，但Triplet loss值还没有达到0，此时网络通过恰当的学习可以不断降低损失值。
$$||f(x_i^a)-f(x_i^p)|{|}_2^2<||f(x_i^a)-f(x_i^n)|{|}_2^2<||f(x_i^a)-f(x_i^p)|{|}_2^2+\alpha$$
（c）hard triplets（困难三元组）：指负样本与基准样本间的距离小于正样本与基准样本间的距离，这是网络最难学习的样本组，此时的损失值会出现较大的震荡。
$$||f(x_i^a)-f(x_i^p)|{|}_2^2>||f(x_i^a)-f(x_i^n)|{|}_2^2$$

而一般三元组非常适合网络的前期训练，能够帮助训练网络的收敛，并且同时可以得到大量比较有效的统计信息。
困难三元组则在网络训练后期起到很好的学习作用，能够帮助提升网络的性能。让网络学习一些很难的样本特征，可以大大提高训练网络的分类能力，尤其是对难以判断的样本的判别能力。

• 优点

基于三元组损失的网络模型可以很好的对细节进行区分，尤其是在图像分类任务重，当两个输入很相似时，三元组损失对这两个差异性较小的输入向量可以学习到更好的表示，从而在分类任务重表现出色。

• 缺点

虽然Triplet loss很有效，但也有缺点：三元组的选取导致数据的分布并不一定均匀，所以在模型训练过程表现很不稳定，而且收敛慢，需要根据结果不断调节参数，而且Triplet loss比分类损失更容易过拟合。

所以，大多数情况下，我们会把这种方法放在模型的预训练过程中，或者和softmax函数（分类损失）结合在一起使用，以稳定训练过程。

• Pytroch实现
  

triplet_loss = nn.TripletMarginLoss(margin=1.0, p=2)
anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)
output = triplet_loss(anchor, positive, negative)
output.backward()

GitHub上找到了一个三元组损失的类，如下。

#!/usr/bin/python
# -*- encoding: utf-8 -*-


import torch
import torch.nn as nn


class TripletLoss(nn.Module):
    '''
    Compute normal triplet loss or soft margin triplet loss given triplets
    '''
    def __init__(self, margin=None):
        super(TripletLoss, self).__init__()
        self.margin = margin
        if self.margin is None:  # if no margin assigned, use soft-margin
            self.Loss = nn.SoftMarginLoss()
        else:
            self.Loss = nn.TripletMarginLoss(margin=margin, p=2)

    def forward(self, anchor, pos, neg):
        if self.margin is None:
            num_samples = anchor.shape[0]
            y = torch.ones((num_samples, 1)).view(-1)
            if anchor.is_cuda: y = y.cuda()
            ap_dist = torch.norm(anchor-pos, 2, dim=1).view(-1)
            an_dist = torch.norm(anchor-neg, 2, dim=1).view(-1)
            loss = self.Loss(an_dist - ap_dist, y)
        else:
            loss = self.Loss(anchor, pos, neg)

        return loss


if __name__ == '__main__':
    pass

参考文献

1. Latex数学公式语法
2. 深度学习-Loss函数
3. pytorch各种交叉熵函数的汇总具体使用
4. 一文搞懂熵（Entropy），交叉熵（Cross-Entropy）
5. 三元组损失与TensorFlow在线三元组挖掘
6. 深度学习之三元组损失原理与选取策略
7. Pytroch实现三元组损失