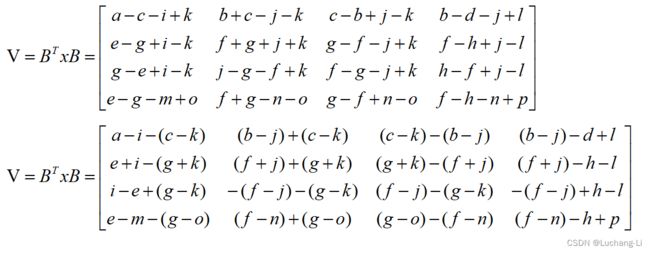winograd卷积实践

winograd卷积基本原理参考

Winograd算法实现卷积原理_Luchang-Li的博客-CSDN博客_optimizing batched winograd convolution on gpus

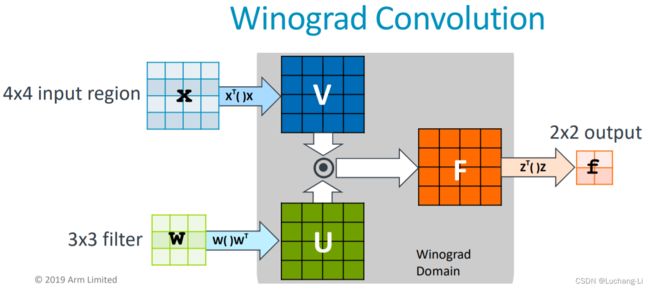
winograd卷积图示：

注意这张图里面隐藏了input和output channel。实际上每个空间维度里面还包含了batch和in/out channel维度。 

输入数据格式为[n, h, w, c]，input transform后格式原始的论文[Fast Algorithms for Convolutional Neural Networks]的格式是[ho/2*w0/2, 16, n, ci]，实际也常用[n, ho/2*w0/2, 16, 1, ci]。ho, wo是输出height和width尺寸，除以2是因为两个相邻元素共享一个4x4矩阵。

输入变换是空间维乘以变换矩阵，由于每个空间维元素实际上对应于一个2维向量，实际上相当于每个空间维元素对应的的向量之间做各种乘加运算。如下图。

weight原始格式为[c0, ci, h, w]，这里h = w = 3, 先处理为[h, w, ci, co], 然后weight transform转换后为[4*4, ci, co]。

转换后的输入和weight做batch矩阵乘得到数据格式为[n, ho/2*w0/2, 4*4, 1, co]。

最后做输出transform得到格式为[n, ho/2*w0/2, 2*2, co]，也就是[n, ho, wo, co]

输入变换计算过程，假设输入x的4x4空间维内容标记为a-p（可以借助Matlab符号计算来得到转换结果矩阵与x的计算关系）：

端侧推理引擎如mnn由于通常没有或只有很少的shared mem，线程之间数据交换能力比较弱，通常按照这个流程把整个计算流程拆分为了三个步骤而不是写在一个完整的kernel：input transform, matmul, output transform。而权重在推理时是常量，可以通过常量折叠提前做好weight transform。

对于NHWC的数据，通常采用每个thread读取4x4，并且channel深度为4的输入数据做input transform。

矩阵乘部分shape是[n, ho/2*w0/2, 16, 1, ci] * [16, ci, co]，最内层的[1, ci] * [ci, co]可以考虑通过每个线程计算1x1*1x4 tile大小矩阵乘（与常用的4x1*1x4或8x1*1x8 tile原理相同，参考[施工中] CUDA GEMM 理论性能分析与 kernel 优化 - 知乎）。但这个矩阵乘shape太小，导致每个线程计算量小，而且需要创建太多线程。

另一种可能的做法是input transform输出的shape格式是[n, 16, ho/2*w0/2, ci]，然后与weight transform后的[16, ci, co]做矩阵乘，这样最内层的矩阵乘大小显著增大为[ho/2*w0/2, ci]*[ci, co]，更有利于性能优化。

跟卷积通过im2row+matmul的实现相比，由于相邻的卷积框有重复的数据，对于3x3 stride=1，im2row每个位置数据读取一次，写出9次，因此im2row写回和matmul读取数据量增大了9倍。

winograd input transform相当于4x4 kernel, stride = 2，input transform写回和matmul读取数据数据量相比输入增大4倍。

遗留问题：相比NHWC或者NCHW输入格式，NCHW4输入格式对winograd卷积会带来什么样的帮助？