人工智能--遗传算法求解TSP问题
文章目录
- 前言
- 一、遗传算法的概念
-
-
- 遗传算法(Genetic Algorithm, GA):
-
- 二、解决的问题对象
- 三、 程序步骤
-
- 1.针对TSP问题,确定编码
- 2.针对TSP问题,适应度函数可定义为
- 3.针对TSP问题,确定交叉规则
-
-
- 对于采用整数编码表示的染色体,可以有以下交叉规则:
- (1)顺序交叉法(Order Crossover, OX)
- (2)基于顺序的交叉法(Order-Based Crossover, OBX)
- (3)基于位置的交叉法(Position-based Crossover, PBX)
-
- 4.确定变异规则,以下变异规则选其一
-
-
- (1) 基于位置的变异
- (2) 基于次序的变异
- (3) 打乱变异
- (4) 翻转切片编译
-
- 5.根据种群选择算法
-
-
- (1)锦标赛算法(Tournament Selection)
- (2)轮盘赌选择算法(Roulette Wheel Selection)
-
- 注:代码不再一一列举,下面给出完整代码
-
- 1.轮盘赌算法
- 2.锦标赛算法
- 四、总结
前言
本文介绍使用遗传算法求解TSP问题,其中包含轮盘赌算法以及锦标赛算法,在总结处会对这两种算法进行优劣对比。
一、遗传算法的概念
遗传算法(Genetic Algorithm, GA):
是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
二、解决的问题对象
使用遗传算法求下图中从北京出发经过其他四个城市之后回到北京的最短路径,两个城市之间的距离如图所示:
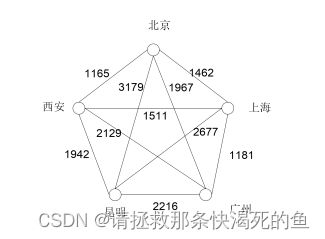
三、 程序步骤
1.针对TSP问题,确定编码
可采用十进制编码法,对城市进行编号,每个城市分别用1到n之间不同的整数表示,n个整数的一个排列就代表了旅行商问题。如对于五城市旅行商问题,用1到5分别代表城市北京、上海、广州、昆明、西安,其中一个可能解为:1 5 2 3 4 1(北京-西安-上海-广州-昆明-北京)定义个体类,每个个体类中包括基因(城市路线)和适应度,核心代码如下:
class Individual:
def __init__(self, genes=None):
if genes = None:
genes = [i for i in range(city_num)]
random.shuffle(genes)
self.genes = genes
self.fitness = self.evalute_fitness()
#计算个体的适应度
def evaluate_fitness(self):
dis = 0
for i in range(city_num - 1):
dis += city_dist_mat[self.genes[i]][self.genes[i+1]]
if i == city_num - 2:
dis += city_dist_mat[self.genes[i + 1]][0]#回到0
if num_person_idx % 20 == 0:
dis_list.append(dis)
return 1/dis
2.针对TSP问题,适应度函数可定义为
3.针对TSP问题,确定交叉规则
对于采用整数编码表示的染色体,可以有以下交叉规则:
(1)顺序交叉法(Order Crossover, OX)
在两个父代染色体中随机选择起始和结束位置,将父代染色体1该区域内的基因复制到子代1相同位置上,再在父代染色体2上将子代1中缺少的基因按照顺序填入。另一个子代以类似方式得到。
(2)基于顺序的交叉法(Order-Based Crossover, OBX)
在两个父代染色体中随机选择几个位置,位置可以不连续,先在父代染色体2中找到父代染色体1被选中基因的位置,再用父代染色体2中其余的基因生成子代,并保证位置对应,将父代染色体1中被选择的基因按顺序放入子代剩余位置中。另一个子代以类似方式得到。
(3)基于位置的交叉法(Position-based Crossover, PBX)
对于选定的父代染色体父代1和父代2,首先随机产生一组位置。对于这些位置上的基因,子代1从父代2中直接得到,子代1其他位置的基因,按照顺序从父代1中选取那些不相重的基因。子代2也进行类似的处理。PBX与OBX相比,生成子代的“基础”基因来源不同,PBX来自被选中基因,OBX来自剩余基因。
4.确定变异规则,以下变异规则选其一
(1) 基于位置的变异
该方法随机地产生两个变异位,然后将第二个变异位上的基因移动到第一个变异位之前。如假定变异位为2和5,对整数编码的TSP问题,变异前后的变化为:
变异前:1 2 3 4 5
变异后:1 5 2 3 4
(2) 基于次序的变异
该方法随机地产生两个变异位,然后交换这两个变异位上的基因。如假定变异位为2和5,对整数编码的TSP问题,变异前后的变化为:
变异前:1 2 3 4 5
变异后:1 5 3 4 2
(3) 打乱变异
该方法随机地选取染色体上的一段,然后打乱在该段内的基因次序。如随机选择段的染色体为第二到第五位,对整数编码的TSP问题,其中一种变异的结果为:
变异前:1 2 3 4 5
变异后:1 3 5 4 2
(4) 翻转切片编译
该方法随机产生两个变异位,作为起始位置和结束位置,将两位置之间的基因翻转,变异前后的变化为:
变异前:1 2 3 4 5
变异后:1 4 3 2 5
5.根据种群选择算法
(1)锦标赛算法(Tournament Selection)
锦标赛方法选择策略每次从种群中取出一定数量个体,然后选择其中最好的一个进入。
子代种群。重复该操作,直到新的种群规模达到原来的种群规模。具体的操作步骤如下:
- 确定每次选择的个体数量(本文以占种群中个体个数的百分比表示)。
- 从种群中随机选择个体(每个个体入选概率相同) 构成组,根据每个个体的适应度值,
选择其中适应度值最好的个体进入子代种群。 - 重复步骤2,得到的个体构成新一代种群。
(2)轮盘赌选择算法(Roulette Wheel Selection)
它模拟博彩游戏的轮盘赌。一个轮盘被划分为N个扇形表示种群的一个染色体,而每个扇形的面积与它所表示的染色体的适应值成正比,为了选择种群中的个体,设想有一个指针指向轮盘,转动轮盘,当轮盘停止后,指针所之乡的染色体被选择。因为一个染色体的适应值越大表示该染色体的扇形面积就越大,因此它被选择的可能性也就越大。
步骤六 根据选定的编码、遗传操作实现基本遗传算法,编写代码,调试程序。输出结果。
注:代码不再一一列举,下面给出完整代码
1.轮盘赌算法
#!/usr/bin/env python
# coding: utf-8
# In[32]:
import numpy as np
import copy
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import random
# In[33]:
#准备好距离矩阵
city_num = 5
city_dist_mat = np.zeros([city_num, city_num])
city_dist_mat[0][1] = city_dist_mat[1][0] = 1165
city_dist_mat[0][2] = city_dist_mat[2][0] = 1462
city_dist_mat[0][3] = city_dist_mat[3][0] = 3179
city_dist_mat[0][4] = city_dist_mat[4][0] = 1967
city_dist_mat[1][2] = city_dist_mat[2][1] = 1511
city_dist_mat[1][3] = city_dist_mat[3][1] = 1942
city_dist_mat[1][4] = city_dist_mat[4][1] = 2129
city_dist_mat[2][3] = city_dist_mat[3][2] = 2677
city_dist_mat[2][4] = city_dist_mat[4][2] = 1181
city_dist_mat[3][4] = city_dist_mat[4][3] = 2216
#标号说明
#list_city = ['0_北京', '1_西安', '2_上海', '3_昆明', '4_广州']
# In[34]:
#1.定义个体类,包括基因(城市路线)和适应度
num_person_idx = 0
num_person = 0
dis_list = []
class Individual:
def __init__(self, genes = None):
global num_person
global dis_list
global num_person_idx
num_person_idx += 1
if num_person_idx % 20 == 0:
num_person += 1
self.genes = genes
if self.genes == None:
genes = [0]*5
temp = [0]*4
temp = [i for i in range(1,city_num)]########################################################################
random.shuffle(temp)
genes[1:] = temp
genes[0] = 0
self.genes = genes
self.fitness = self.evaluate_fitness()
else:
self.fitness = float(self.evaluate_fitness())
#2. #计算个体的适应度
def evaluate_fitness(self):
dis = 0
for i in range(city_num - 1):
dis += city_dist_mat[self.genes[i]][self.genes[i+1]]
if i == city_num - 2:
dis += city_dist_mat[self.genes[i + 1]][0]#回到0
if num_person_idx % 20 == 0:
dis_list.append(dis)
return 1/dis
# In[35]:
def copy_list(old):
new = []
for element in old:
new.append(element)
return new
def sort_win_num(group):
for i in range(len(group)):
for j in range(len(group) - i - 1):
# print('group[j].fitness_type', type(group[j].fitness))
if group[j].fitness < group[j+1].fitness:
temp = group[j]
group[j] = group[j+1]
group[j+1] = temp
return group
#定义Ga类
#3~5,交叉、变异、更新种群,全部在Ga类中实现
class Ga:
#input_为城市间的距离矩阵
def __init__(self, input_):
#声明一个全局变量
global city_dist_mat
city_dist_mat = input_
#当代的最佳个体########################################此处做了更改
#self.best = None
self.best = Individual(None)
# print("BBBBBBbest.fitness",self.best.fitness)
#种群
self.individual_list = []
#每一代的最佳个体
self.result_list = []
#每一代个体对应的最佳适应度
self.fitness_list = []
#交叉,这里采用交叉变异
def cross(self):
new_gen = []
#随机选取一段,含有num_cross个数字(城市)
num_cross = 3#后期可能需要调试的参数,考虑到实际问题里只有5个城市,所以认为3较为合适
for i in range(0, len(self.individual_list) - 1, 2):
parent_gen1 = copy_list(self.individual_list[i].genes)
parent_gen2 = copy_list(self.individual_list[i+1].genes)
# print("parent_gen1",parent_gen1)
# print("parent_gen2",parent_gen2)
index1_1 = 0
index1_2 = 0
index2_1 = 0
index2_2 = 0
#定义一个下表列表
index_list = [0]*3
for i in range(city_num - 3):#就是2,即0,1
index_list[i] = i + 1
index1_1 = random.choice(index_list)
index1_2 = index1_1 + 2
index2_1 = random.choice(index_list)
index2_2 = index2_1 + 2
choice_list1 = parent_gen1[index1_1:index1_2 + 1]
choice_list2 = parent_gen2[index2_1:index2_2 + 1]
# print("choice_list1",choice_list1)
# print("choice_list2",choice_list2)
#利用这一段生成两个子代,下面的赋值只是为了获取长度,所以用哪个父代能可以
#也可以直接用city_num直接代替
son_gen1 = [0]*city_num
son_gen2 = [0]*city_num
# print('son_gen1_size = ',len(son_gen1))
# print('son_gen2_size = ',len(son_gen2))
# print("index1_1 == ",index1_1)
# print("index1_2 == ",index1_2)
# print("index2_1 == ",index2_1)
# print("index2_2 == ",index2_2)
#找到之后进行交叉,分别得到son_gen1,son_gen2
#先把选中的段复制进去
son_gen1[index1_1: index1_2 + 1] = choice_list1
son_gen2[index2_1: index2_2 + 1] = choice_list2
# print("now, son_gen1 = ", son_gen1)
# print("now, son_gen2 = ", son_gen2)
#然后左、右“查漏补缺”
temp1 = choice_list1
temp2 = choice_list2
if index1_1 == 0:
pass
else:
for i in range(index1_1):
for j in range(city_num):
#如果父代2里面的这个当初没被选中,那就加入son_gene1
if parent_gen2[j] not in choice_list1:
son_gen1[i] = parent_gen2[j]
#这个时候要扩增choice_list1, 这样parent_gen2里面未被选中的元素才会一个个被遍历到#1
choice_list1.append(parent_gen2[j])
#找到之后马上break,防止被覆盖
break
choice_list1 = temp1
if index1_2 == city_num - 1:
pass
else:
for i in range(index1_2 + 1, city_num):
for j in range(city_num):
if parent_gen2[j] not in choice_list1:
son_gen1[i] = parent_gen2[j]
#这个时候要扩增choice_list1, 这样parent_gen2里面未被选中的元素才会一个个被遍历到#2
choice_list1.append(parent_gen2[j])
#找到之后马上break,防止被覆盖
break
#son_gen2亦是如此
if index2_1 == 0:
pass
else:
for i in range(index2_1):
for j in range(city_num):
#如果父代1里面的这个当初没被选中,那就加入son_gen2
if parent_gen1[j] not in choice_list2:
son_gen2[i] = parent_gen1[j]
#这个时候要扩增choice_list2, 这样parent_gen1里面未被选中的元素才会一个个被遍历到#3
choice_list2.append(parent_gen1[j])
#找到之后马上break,防止被覆盖
break
choice_list2 = temp2
if index2_2 == city_num - 1:
pass
else:
for i in range(index2_2 + 1, city_num):
for j in range(city_num):
if parent_gen1[j] not in choice_list2:
# print("i == ", i)
son_gen2[i] = parent_gen1[j]
#这个时候要扩增choice_list2, 这样parent_gen1里面未被选中的元素才会一个个被遍历到#4
choice_list2.append(parent_gen1[j])
#找到之后马上break,防止被覆盖
break
#新生成的子代基因加入new_gene列表
# print('son_gen1 = ',son_gen1)
# print('son_gen2 = ',son_gen2)
new_gen.append(Individual(son_gen1))
#print('new_gen[-1].genes', new_gen[-1].genes)
new_gen.append(Individual(son_gen2))
return new_gen
#变异
def mutate(self, new_gen):
mutate_p = 0.02#待调参数
index_list = [0]*(city_num-1)
index_1 = 1
index_2 = 1
for i in range(city_num - 1):
index_list[i] = i + 1
for individual in new_gen:
if random.random() < mutate_p:
# change += 1
#如果变异,采用基于位置的变异,方便起见,直接使用上面定义的index列表
index_l = random.choice(index_list)
# index_2 = (index_1 + 2) % city_num#这里让间隔为2的两个城市进行交换
index_2 = random.choice(index_list)
while index_1 == index_2:
index_2 = random.choice(index_list)
#交换
temp = individual.genes[index_1]
individual.genes[index_1] = individual.genes[index_2]
individual.genes[index_2] = temp
#变异结束,与老一代的进行合并
self.individual_list += new_gen
#选择
def select(self):
#在此选用轮盘赌算法
#考虑到5的阶乘是120,所以可供选择的个体基数应该适当大一些,
#在此每次从种群中选择6个,进行轮盘赌,初始化60个个体,同时适当调高变异的概率
select_num = 6
select_list = []
for i in range(select_num):
gambler = random.choice(self.individual_list)
gambler = Individual(gambler.genes)
select_list.append(gambler)
#求出这些fitness之和
sum = 0
for i in range(select_num):
sum += select_list[i].fitness
sum_m = [0]*select_num
#实现概率累加
for i in range(select_num):
for j in range(i+1):
sum_m[i] += select_list[j].fitness
sum_m[i] /= sum
new_select_list = []
p_num = 0#随机数
for i in range(select_num):
p_num = random.uniform(0,1)
if p_num>0 and p_num < sum_m[0]:
new_select_list.append(select_list[0])
elif p_num>= sum_m[0] and p_num < sum_m[1]:
new_select_list.append(select_list[1])
elif p_num >= sum_m[1] and p_num < sum_m[2]:
new_select_list.append(select_list[2])
elif p_num >= sum_m[2] and p_num < sum_m[3]:
new_select_list.append(select_list[3])
elif p_num >= sum_m[3] and p_num < sum_m[4]:
new_select_list.append(select_list[4])
elif p_num >= sum_m[4] and p_num < sum_m[5]:
new_select_list.append(select_list[5])
else:
pass
#将新生成的一代替代父代种群
self.individual_list = new_select_list
#更新种群
def next_gen(self):
#交叉
new_gene = self.cross()
#变异
self.mutate(new_gene)
#选择
self.select()
#获得这一代的最佳个体
# print("**************************************")
# print('self.best.fitness = ', self.best.fitness)
# print('now, best.fitness = ', self.best.fitness)
for individual in self.individual_list:
if individual.fitness > self.best.fitness:
self.best = individual
# print("更换了最优路径")
# print('now, best.fitness = ', self.best.fitness)
def train(self):
#随机出初代种群#
individual_num = 60
self.individual_list = [Individual() for _ in range(individual_num)]
#迭代
gen_num = 100
for i in range(gen_num):
#从当代种群中交叉、变异、选择出适应度最佳的个体,获得子代产生新的种群
self.next_gen()
#连接首位
# print("i = ", i)
result = copy.deepcopy(self.best.genes)
result.append(result[0])
self.result_list.append(result)
self.fitness_list.append(self.best.fitness)
print(self.result_list[-1])
print('距离总和是:', 1/self.fitness_list[-1])
# return self.result_list, self.fitness_list
def draw(self):
x_list = [i for i in range(num_person)]
y_list = dis_list
plt.rcParams['figure.figsize'] = (60, 45)
plt.plot(x_list, y_list, color = 'g')
plt.xlabel('Cycles',size = 50)
plt.ylabel('Route',size = 50)
x = np.arange(0, 910, 20)
y = np.arange(7800, 12000, 100)
plt.xticks(x)
plt.yticks(y)
plt.title('Trends in distance changes', size = 50)
plt.tick_params(labelsize=30)
# plt.savefig("D:\AI_pictures\遗传算法求解TSP问题_1_轮盘赌算法")
plt.show()
route = Ga(city_dist_mat)
route.train()
route.draw()
2.锦标赛算法
#!/usr/bin/env python
# coding: utf-8
import numpy as np
import copy
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import random
# In[186]:
#准备好距离矩阵
city_num = 5
city_dist_mat = np.zeros([city_num, city_num])
city_dist_mat[0][1] = city_dist_mat[1][0] = 1165
city_dist_mat[0][2] = city_dist_mat[2][0] = 1462
city_dist_mat[0][3] = city_dist_mat[3][0] = 3179
city_dist_mat[0][4] = city_dist_mat[4][0] = 1967
city_dist_mat[1][2] = city_dist_mat[2][1] = 1511
city_dist_mat[1][3] = city_dist_mat[3][1] = 1942
city_dist_mat[1][4] = city_dist_mat[4][1] = 2129
city_dist_mat[2][3] = city_dist_mat[3][2] = 2677
city_dist_mat[2][4] = city_dist_mat[4][2] = 1181
city_dist_mat[3][4] = city_dist_mat[4][3] = 2216
#标号说明
#list_city = ['0_北京', '1_西安', '2_上海', '3_昆明', '4_广州']
#1.定义个体类,包括基因(城市路线)和适应度
num_person_idx = 0
num_person = 0
dis_list = []
class Individual:
def __init__(self, genes = None):
global num_person
global dis_list
global num_person_idx
num_person_idx += 1
if num_person_idx % 20 == 0:
num_person += 1
self.genes = genes
if self.genes == None:
genes = [0]*5
temp = [0]*4
temp = [i for i in range(1,city_num)]
random.shuffle(temp)
genes[1:] = temp
genes[0] = 0
self.genes = genes
# print("init_self.genes = ",self.genes)
self.fitness = self.evaluate_fitness()
# self.fitness = fitness
# dis_list.append(-1.0)
else:
self.fitness = float(self.evaluate_fitness())
# print('self.fitness', self.fitness)
#2. #计算个体的适应度
def evaluate_fitness(self):
dis = 0
# print("city_num - 1 = ", city_num - 1)
#print("***************")
#print(city_dist_mat)
# print("self.genes = ", self.genes)
for i in range(city_num - 1):
dis += city_dist_mat[self.genes[i]][self.genes[i+1]]
# print("he: ", dis)
if i == city_num - 2:
# print("adding tail ",self.genes[i + 1], 0, city_dist_mat[self.genes[i + 1]][0])
dis += city_dist_mat[self.genes[i + 1]][0]#回到0
# print('dis = ', dis)
if num_person_idx % 20 == 0:
dis_list.append(dis)
return 1/dis
# In[188]:
def copy_list(old):
new = []
for element in old:
new.append(element)
return new
def sort_win_num(group):
for i in range(len(group)):
for j in range(len(group) - i - 1):
# print('group[j].fitness_type', type(group[j].fitness))
if group[j].fitness < group[j+1].fitness:
temp = group[j]
group[j] = group[j+1]
group[j+1] = temp
return group
#定义Ga类
#3~5,交叉、变异、更新种群,全部在Ga类中实现
class Ga:
#input_为城市间的距离矩阵
def __init__(self, input_):
#声明一个全局变量
global city_dist_mat
city_dist_mat = input_
#self.best = None
self.best = Individual(None)
# print("BBBBBBbest.fitness",self.best.fitness)
#种群
self.individual_list = []
#每一代的最佳个体
self.result_list = []
#每一代个体对应的最佳适应度
self.fitness_list = []
#交叉,这里采用交叉变异
def cross(self):
new_gen = []
#随机选取一段,含有num_cross个数字(城市)
num_cross = 3#后期可能需要调试的参数,考虑到实际问题里只有5个城市,所以认为3较为合适
for i in range(0, len(self.individual_list) - 1, 2):
parent_gen1 = copy_list(self.individual_list[i].genes)
parent_gen2 = copy_list(self.individual_list[i+1].genes)
# print("parent_gen1",parent_gen1)
# print("parent_gen2",parent_gen2)
index1_1 = 0
index1_2 = 0
index2_1 = 0
index2_2 = 0
#定义一个下表列表
index_list = [0]*3
for i in range(city_num - 3):#就是2,即0,1
index_list[i] = i + 1
index1_1 = random.choice(index_list)
index1_2 = index1_1 + 2
index2_1 = random.choice(index_list)
index2_2 = index2_1 + 2
choice_list1 = parent_gen1[index1_1:index1_2 + 1]
choice_list2 = parent_gen2[index2_1:index2_2 + 1]
#利用这一段生成两个子代,下面的赋值只是为了获取长度,所以用哪个父代能可以
#也可以直接用city_num直接代替
son_gen1 = [0]*city_num
son_gen2 = [0]*city_num
#找到之后进行交叉,分别得到son_gen1,son_gen2
#先把选中的段复制进去
son_gen1[index1_1: index1_2 + 1] = choice_list1
son_gen2[index2_1: index2_2 + 1] = choice_list2
#然后左、右“查漏补缺”
temp1 = choice_list1
temp2 = choice_list2
if index1_1 == 0:
pass
else:
for i in range(index1_1):
for j in range(city_num):
#如果父代2里面的这个当初没被选中,那就加入son_gene1
if parent_gen2[j] not in choice_list1:
son_gen1[i] = parent_gen2[j]
#这个时候要扩增choice_list1, 这样parent_gen2里面未被选中的元素才会一个个被遍历到#1
choice_list1.append(parent_gen2[j])
#找到之后马上break,防止被覆盖
break
choice_list1 = temp1
if index1_2 == city_num - 1:
pass
else:
for i in range(index1_2 + 1, city_num):
for j in range(city_num):
if parent_gen2[j] not in choice_list1:
son_gen1[i] = parent_gen2[j]
#这个时候要扩增choice_list1, 这样parent_gen2里面未被选中的元素才会一个个被遍历到#2
choice_list1.append(parent_gen2[j])
#找到之后马上break,防止被覆盖
break
#son_gen2亦是如此
if index2_1 == 0:
pass
else:
for i in range(index2_1):
for j in range(city_num):
#如果父代1里面的这个当初没被选中,那就加入son_gen2
if parent_gen1[j] not in choice_list2:
son_gen2[i] = parent_gen1[j]
#这个时候要扩增choice_list2, 这样parent_gen1里面未被选中的元素才会一个个被遍历到#3
choice_list2.append(parent_gen1[j])
#找到之后马上break,防止被覆盖
break
choice_list2 = temp2
if index2_2 == city_num - 1:
pass
else:
for i in range(index2_2 + 1, city_num):
for j in range(city_num):
if parent_gen1[j] not in choice_list2:
# print("i == ", i)
son_gen2[i] = parent_gen1[j]
#这个时候要扩增choice_list2, 这样parent_gen1里面未被选中的元素才会一个个被遍历到#4
choice_list2.append(parent_gen1[j])
#找到之后马上break,防止被覆盖
break
#新生成的子代基因加入new_gene列表
# print('son_gen1 = ',son_gen1)
# print('son_gen2 = ',son_gen2)
new_gen.append(Individual(son_gen1))
#print('new_gen[-1].genes', new_gen[-1].genes)
new_gen.append(Individual(son_gen2))
return new_gen
#变异
def mutate(self, new_gen):
change = 0
mutate_p = 0.02#待调参数
index_list = [0]*(city_num-1)
index_1 = 1
index_2 = 1
for i in range(city_num - 1):
index_list[i] = i + 1
for individual in new_gen:
if random.random() < mutate_p:
change += 1
#如果变异,采用基于位置的变异,方便起见,直接使用上面定义的index列表
index_l = random.choice(index_list)
# index_2 = (index_1 + 2) % city_num#这里让间隔为2的两个城市进行交换
index_2 = random.choice(index_list)
while index_1 == index_2:
index_2 = random.choice(index_list)
#交换
temp = individual.genes[index_1]
individual.genes[index_1] = individual.genes[index_2]
individual.genes[index_2] = temp
#变异结束,与老一代的进行合并
self.individual_list += new_gen
# print(f'发生了{change}次变异')
#选择
def select(self):
#在此选用锦标赛算法
#考虑到5的阶乘是120,所以感觉4个个体一组较为合适,所以group_num = 30,暂定每一代保留60
# print("到达select*************************")
group_num = 30#待调参数
group_size = 4
win_num = 2#60/15
#锦标赛的胜者列表
winners = []
for i in range(group_num):
#定义临时列表,存储够一组为止
group = []
for j in range(group_size):
gen_player = random.choice(self.individual_list)
gen_player = Individual(gen_player.genes)##################
group.append(gen_player)
#存储完一组之后选出适应度最大的前4个
group = sort_win_num(group)
winners += group[: win_num]
# print("winners[0].genes = ", winners[0].genes)
# print("1/winners[0].fitness",1/winners[0].fitness)
# print("winners[1].genes = ", winners[1].genes)
# print("1/winners[1].fitness",1/winners[1].fitness)
#选择结束,生成全新一代,赋值给self.individual_list
self.individual_list = winners
# print('selcetselect')
#更新种群
def next_gen(self):
#交叉
new_gene = self.cross()
#变异
self.mutate(new_gene)
#选择
self.select()
#获得这一代的最佳个体
# print("**************************************")
# print('self.best.fitness = ', self.best.fitness)
# print('now, best.fitness = ', self.best.fitness)
for individual in self.individual_list:
if individual.fitness > self.best.fitness:
self.best = individual
# print("更换了最优路径")
# print('now, best.fitness = ', self.best.fitness)
def train(self):
#随机出初代种群#
individual_num = 60
self.individual_list = [Individual() for _ in range(individual_num)]
#迭代
gen_num = 100
for i in range(gen_num):
#从当代种群中交叉、变异、选择出适应度最佳的个体,获得子代产生新的种群
self.next_gen()
#连接首位
# print("i = ", i)
result = copy.deepcopy(self.best.genes)
result.append(result[0])
self.result_list.append(result)
self.fitness_list.append(self.best.fitness)
print(self.result_list[-1])
print('距离总和是:', 1/self.fitness_list[-1])
# return self.result_list, self.fitness_list
def draw(self):
x_list = [i for i in range(num_person)]
y_list = dis_list
plt.rcParams['figure.figsize'] = (60, 45)
plt.plot(x_list, y_list, color = 'g')
plt.xlabel('Cycles',size = 50)
plt.ylabel('Route',size = 50)
x = np.arange(0, 910, 20)
y = np.arange(7800, 12000, 100)
plt.xticks(x)
plt.yticks(y)
plt.title('Trends in distance changes', size = 50)
plt.tick_params(labelsize=30)
plt.savefig("D:\AI_pictures\遗传算法求解TSP问题_1")
plt.show()
route = Ga(city_dist_mat)
route.train()
route.draw()
四、总结
- 遗传算法是一种基于解空间求解的算法,每一次只能从大体上让求解域更接近最优解,这是由于需要借助变异的力量让求解域免于进入次优解的“局部低谷”之中,可变异同时会带来差解。针对于这个问题,由于数据量较小,我们可以将变异的种群的fitness与现有种群进行比较,若低于最低值,则不将变异个体加入。但显然面对庞大数据时这种思路实现上会严重耗时,降低效率。
- 轮盘赌算法的表现显然不如锦标赛算法,锦标赛算法在同一个问题下轮数为100时已经能稳定收敛到最优解,但轮盘赌在5倍于它的情况下仍不能保证收敛。
- 每种算法的每一次调参都会面临无数种选择,尤其是参数较多时,各种排列组合要尝试很多遍,最好能先进行合理猜想参数之间的关系,然后实验验证,周期过大时波动反而会更加明显,可以分析得出变异率的影响较大。
