卷积神经网络学习：CNN

CNN 十分擅长图像处理工作。你可能会问，为什么我们之前学过的全连接神经网络不能用来处理图像呢？

答案是：可以，但没必要。

在图片处理工作中，我们把组成图片的每个像素点的信息当做输入层 (input layer)，对于黑白像素，可以用 0 和 1 来表示，对于彩色像素，可以用 RGB 值来表示。

对于全连接神经网络，我们要将所有的像素点都输入神经网络，然后构建一个庞大的神经网络模型。

如上图所示，第一层的神经元可能只能识别不同的颜色，第二层的神经元可能可以识别特定的纹理，再往后的某一层神经元也许就能识别一个复杂的物体，比如蜂巢或者汽车轮胎。

但问题是，如果我们使用全连接神经网络，一张 100×100 的彩色图片，光输入层就有 100×100×3=30000 个参数，如果是整个神经网络，这就太庞大了。

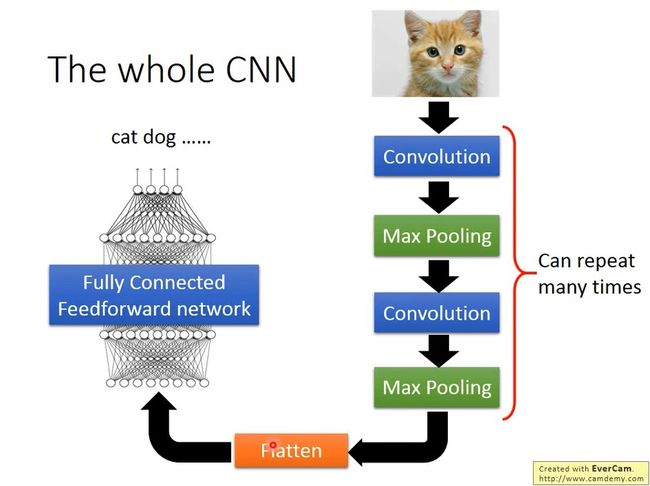
CNN 整体结构：

 

 

一张图片会由很多个像素 (Pixel) 组成的矩阵表示，作为输入层。

经过中间层的卷积 (Convolution) 和最大池化 (Max Pooling)，我们会得到一个高维的矩阵，这一过程可以重复多次，用以提取更高维度的特征。

然后我们将这个矩阵进行 Flatten 操作，把高维的矩阵 “压平”，将结果输入全连接神经网络中，最后得出结果。

接下来，我们会仔细分析每一个过程中的实现细节和作用。

 卷积（Convolution）：

 

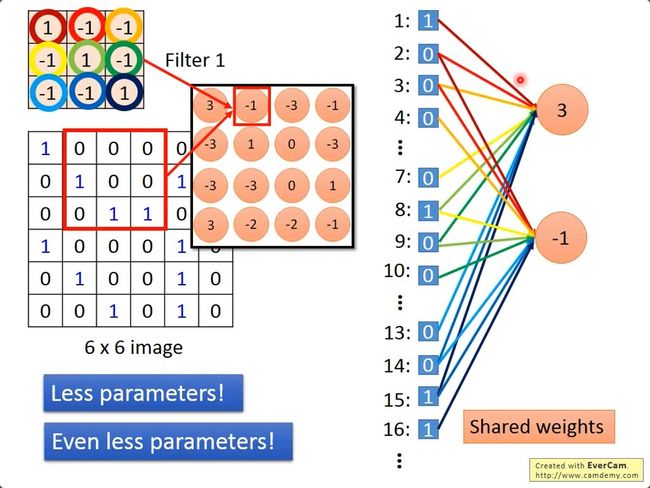
下图中左侧是一张图片，我们用 0 和 1 来表示图片的黑白像素，大小为 6×6 的矩阵。

右侧有两个不同的 filter，他们是大小为 3*3 的矩阵，通过训练得到，我们可以用他们来侦测不同的 pattern，也就是图片的某个特征。

如何侦测呢，我们只需要用这个 filter 和图片矩阵中的某一个部分（3*3 的矩阵）做内积，就可以侦测这一部分的 pattern，然后按照一定的步长移动 filter，就可以获得图片中所有位置含有这个 pattern的状况。 

刚刚我们的图片是黑白的，如果是彩色的图片呢？

我们通常用 RGB 来表示彩色图片，比如，一张图片我们可以用 6 6 3 的矩阵来表示，这时候我们的 filter 也要做出相应的变化，我们用 3 3 3 大小的 filter 去侦测 pattern，如下图所示：

 

在全连接神经网络中，我们用上一层的输出乘以每条边的权重（weight），就得到了下一层的输入值。

我们首先把图片矩阵和 filter 矩阵都展平，变成一个一维的向量，对于这个位置的 filter，我们可以把 filter 中的每个值看成是与对应节点的边的 weight，不参与此次 filter 的节点相连的边的 weight 可以看成 0， filter 之后得到的结果就是卷积层神经元的值。

 

 

max pooling 做的事情就是 sub-sampling，比如，我们可以吧 convolution 之后的结果 4 个一组分组，然后从中选出值最大的那个，这样我们可以让图片中的特征更加突出。

convolution + max pooling 这一过程我们可以执行多次，每次我们都会得到一张比之前更小的 image。

 

还记得我们上一步得到的结果吗，我们得到的 feature map 是一个多维的矩阵，我们可以把它叫做张量 (tensor)，区别于向量 (vector)。

我们要讲这个张量输入到全连接神经网络中，为了让我们的计算更加简便，我们可以把这个张量“压扁”，变成一个一维的向量，或者叫数组，把它作为全连接层的输入，后续的工作就非常简单了，就是一个单纯的全连接神经网络的训练。

 训练中卷积层的维度变化：

 下面我们从一个示例来过一遍整个过程，视频中使用的是 Keras，读者并不需要学习这个框架，此处只是为了演示我们最初的图片矩阵在 CNN 中的维度变化。

假设我们图片是一张黑白的 28×28 大小的图片，如下图所示。 

 

第一次卷积的输入是原始图片，图片是黑白的，所以第一个维度为 1（如果是 RGB 就是 3），所以 input_shape=(1, 28, 28) , 第一层卷积层有 25 个 3×3 大小的 filter，所以卷积操作为 Convolution2D(25, 3, 3)。

在进行完第一次卷积之后，我们得到的输出结果是一个 25×26×26 的张量：25 个 filter对应第一个维度，每个 3×3 的 filter 要对 28×28 的图片上内积 26×26 次，所以后两个维度是 26×26。

然后我们进行池化操作，我们把每个 26×26 的矩阵分成许多个 2×2 的小矩阵，然后从每个小矩阵中选出一个最大的值，对应的操作是 MaxPooling2D((2, 2))，这时候我们就完成了第一卷积+池化的操作。得到的结果为 25×13×13 的张量，可以看成是 25 张 13×13 的小图片，然后对这 25 张图片进行第二次卷积+池化，如下图所示。

在第二次卷积的时候要注意，我们输入的为 Convolution2D(50, 3, 3)，这里并不是说我们每个 filter 也是 3×3 的大小，而是 25×3×3=225 的大小的 filter，50 表示有 50 个 filter，因为在上一步的操作中，我们得到的结果是 25×13×13 的，表示有 25 个 channel，框架会自动帮我们处理中间过程，所以我们传入的参数只需 (50, 3, 3)。

到这一步，卷积的操作就基本结束了，我们剩下要做的事情就是把 50×5×5 的张量变成 1250 大小的向量，然后输入到一个全连接神经网络，用我们之前学过的方法进行训练就行了。

 

CNN 训练常用方法简介

这里我们简单了解一些 CNN 训练中常用的方法和一些概念。在实际的训练过程中，这些方法都已经写在了深度学习的框架里，我们只需要调用相关方法就行。

随机梯度下降（Mini-batch SGD）

随机梯度下降 (SGD) 也称为增量梯度下降，是一种迭代方法，用于优化可微分目标函数。在实际使用过程中，小批量进行参数更新的 mini-batch gradient descent 也常常被叫做 SGD。该方法通过在小批量数据上计算损失函数的梯度而迭代地更新权重与偏置项。

在 CNN 的训练过程中，我们通常会选取一个合适的 batch_size，在每一轮的训练中，我们会从总体训练集中随机取出大小为 batch_size 的样本进行训练，这样我们的计算量就大大减小，同时通过 Mini-batch SGD，我们的模型也可以更快的收敛。

激活函数的选择

我们在逻辑回归的时候接触到了一个函数，sigmoid 函数，这是一种最基本的激活函数。但是我们在 CNN 中常用的是另一种激活函数：ReLU 函数，即线性整流函数（Rectified Linear Unit, ReLU）。他的图像是这样的：

相比于其他的激活函数，ReLU 有很多优势。

1. ReLU 可以更加有效率的梯度下降以及反向传播：避免了梯度爆炸和梯度消失问题
2. 简化计算过程：没有了其他复杂激活函数中诸如指数函数的影响；同时活跃度的分散性使得神经网络整体计算成本下降。

在 CNN 的训练过程中，我们通常使用 ReLU 作为激活函数。

批规范化（Batch Normalization）

批规范化是指在每次随机梯度下降时，通过mini-batch来对相应的activation做规范化操作，使得结果（输出信号各个维度）的均值为0，方差为1。而最后的 “scale and shift” 操作则是为了让因训练所需而“刻意”加入的BN能够有可能还原最初的输入，从而保证整个网络的 capacity。

批规范化可以让我们选择比较大的初始学习率，让训练速度飙涨。以前还需要慢慢调整学习率，甚至在网络训练到一半的时候，还需要想着学习率进一步调小的比例选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性。

如图所示，批规范化通常位于全连接层后、非线性激活函数前。

 

一个简单的 CNN 应用

下面，我们将实现一个简单的 CNN 的网络，使用的框架为 Pytorch，这是一个由 FaceBook 推出的深度学习框架。我们会利用该框架搭建一个简答的 CNN 与 全连接网络的结合，然后实现手写数字的识别。首先我们介绍一下 在 Pytorch 中相关接口的说明：

二维卷积 nn.Conv2d()，该接口的输入为一个 BatchSize×Channels×Height×Width 的张量，注意，Pytorh 对图像/矩阵的存储是通道优先的，该接口的部分参数如下：

• in_channels：输入矩阵/图像的通道数；
• out_channels: 输出矩阵/图像的通道数，对应于卷积核的个数；
• kernel_size: 卷积核的大小，kernel_size = 3 表示卷积核的大小为 3×3，kernel_size=(3,5) 表示卷积核的大小为 3×5；
• stride：表示卷积核行进的步长，stride = 1 表示卷积核在图像的长宽维度上行进的步长均为 1，stride=(2,3) 表示在纵向行进的步长为 2，横向行进的步长为 3；
• padding：图像周围的填充，通常补 0，默认不做 padding;
• bias: 是否使用偏置，默认为 True。

全连接层 nn.Linear()，该接口的输入为 BatchSize×Features，该接口的具体参数如下：

• in_features: 表示该全连接层输入的节点个数；
• out_features: 表示该全连接层输出的节点个数；
• bias: 表示是否使用偏置，默认为 True。

  import argparse
  import torch
  import torch.nn as nn
  import torch.nn.functional as F
  import torch.optim as optim
  from torchvision import datasets, transforms
  
  
  class Net(nn.Module):
      def __init__(self):
          super(Net, self).__init__()
          self.conv1 = nn.Conv2d(1, 20, 5, 1)
          #self.bn1 = nn.
          self.conv2 = nn.Conv2d(20, 50, 5, 1)
          self.fc1 = nn.Linear(4 * 4 * 50, 500)
          self.fc2 = nn.Linear(500, 10)
  
      def forward(self, x):
          x = F.relu(self.conv1(x))
          x = F.max_pool2d(x, 2, 2)
          x = F.relu(self.conv2(x))
          x = F.max_pool2d(x, 2, 2)
          x = x.view(-1, 4 * 4 * 50)
          x = F.relu(self.fc1(x))
          x = self.fc2(x)
          return F.log_softmax(x, dim=1)

  def train(model, train_loader, optimizer, epoch):
      model.train()
      for batch_idx, (data, target) in enumerate(train_loader):
          optimizer.zero_grad()
          output = model(data)
          loss = F.nll_loss(output, target)
          loss.backward()
          optimizer.step()
          if batch_idx % 1000 == 0:
              print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                  epoch, batch_idx * len(data), len(train_loader.dataset),
                         100. * batch_idx / len(train_loader), loss.item()))
  
  
  def test(model, test_loader):
      model.eval()
      test_loss = 0
      correct = 0
      with torch.no_grad():
          for data, target in test_loader:
              output = model(data)
              test_loss += F.nll_loss(output, target, reduction='sum').item()  # sum up batch loss
              pred = output.argmax(dim=1, keepdim=True)  # get the index of the max log-probability
              correct += pred.eq(target.view_as(pred)).sum().item()
  
      test_loss /= len(test_loader.dataset)
  
      print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
          test_loss, correct, len(test_loader.dataset),
          100. * correct / len(test_loader.dataset)))

  def main():
      BATCH_SIZE = 128
      epoches = 5
      lr = 1e-4
      
      torch.manual_seed(1)
      kwargs = {}
      train_loader = torch.utils.data.DataLoader(
          datasets.MNIST('../data', train=True, download=True,
                         transform=transforms.Compose([
                             transforms.ToTensor(),
                             transforms.Normalize((0.1307,), (0.3081,))
                         ])),
          batch_size=BATCH_SIZE, shuffle=True, **kwargs)
      test_loader = torch.utils.data.DataLoader(
          datasets.MNIST('../data', train=False, transform=transforms.Compose([
              transforms.ToTensor(),
              transforms.Normalize((0.1307,), (0.3081,))
          ])),
          batch_size=BATCH_SIZE, shuffle=True, **kwargs)
  
      model = Net()
      optimizer = optim.SGD(model.parameters(), lr=lr)
  
      for epoch in range(1, epoches + 1):
          train(model, train_loader, optimizer, epoch)
          test(model, test_loader)
  
      torch.save(model.state_dict(), "mnist_cnn.pt")
  main()