PyTorch中相对位置自注意力的实现细节
PyTorch中相对位置自注意力的实现细节
原始文档:https://www.yuque.com/lart/ugkv9f/oazsec
文章目录
- PyTorch中相对位置自注意力的实现细节
-
- 参考
- 前言
- 代码分析
-
- 提前的思考
- 背后的动机
- 对应的流程
参考
- AI SUMMER这篇文章写的很好,很直观,很清晰:https://theaisummer.com/positional-embeddings/
前言
这里讨论的相对位置编码的实现策略来自于Music Transformer。
这里有一篇介绍性的文章:https://gudgud96.github.io/2020/04/01/annotated-music-transformer/,图例非常清晰。
首先理解下相对位置自注意力中关于位置嵌入的一些细节。
 相对注意力的一些相关概念。摘自Music Transformer。在不考虑head维度时:
相对注意力的一些相关概念。摘自Music Transformer。在不考虑head维度时:
- E r E^r Er: relative position embedding,大小为 ( L , D h ) (L,D_h) (L,Dh)
- R R R: 来自Shaw论文中引入的相对位置嵌入的中间表示,大小为 ( L , L , D h ) (L,L,D_h) (L,L,Dh)
- S r e l = Q R T S^{rel}=QR^T Srel=QRT: 表示相对位置编码与query的交互结果,大小为 ( L , L ) (L, L) (L,L),即在 D h D_h Dh维度上进行了累加
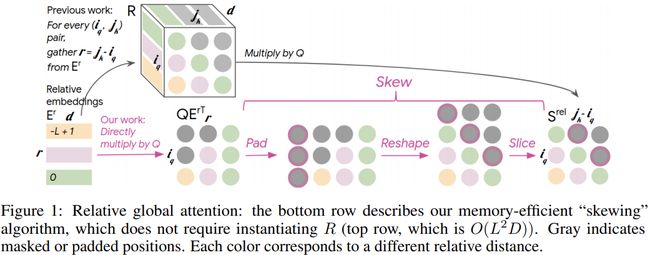
- Music Transformer的一点工作就是将这个会占用较大存储空间的中间表示 R R R去掉,直接得到 S r e l S^{rel} Srel,如下图所示
要注意这里的 E r E^r Er表示的是针对相对位置 − L + 1 → 0 -L+1 \rightarrow 0 −L+1→0的嵌入,最小相对位置为 − L + 1 -L+1 −L+1,最大为0(因为需要考虑因果关系,前面的i看不到后面的j),所以有 L L L个位置。
而对于我们这里将要讨论的不考虑因果关系的情况,最小相对位置为 − N + 1 -N+1 −N+1,最大为 N − 1 N-1 N−1。所以我们的位置嵌入 E r E^r Er形状为 ( 2 N − 1 ) × d (2N-1) \times d (2N−1)×d。
代码分析
首先找份代码来看看,https://github.com/lucidrains/bottleneck-transformer-pytorch/blob/main/bottleneck_transformer_pytorch/bottleneck_transformer_pytorch.py实现的相对位置编码涉及到几个关键的组件:
import torch
import torch.nn as nn
from einops import rearrange
def relative_to_absolute(q):
"""
Converts the dimension that is specified from the axis
from relative distances (with length 2*tokens-1) to absolute distance (length tokens)
borrowed from lucidrains:
https://github.com/lucidrains/bottleneck-transformer-pytorch/blob/main/bottleneck_transformer_pytorch/bottleneck_transformer_pytorch.py#L21
Input: [bs, heads, length, 2*length - 1]
Output: [bs, heads, length, length]
"""
b, h, l, _, device, dtype = *q.shape, q.device, q.dtype
dd = {'device': device, 'dtype': dtype}
col_pad = torch.zeros((b, h, l, 1), **dd)
x = torch.cat((q, col_pad), dim=3) # zero pad 2l-1 to 2l
flat_x = rearrange(x, 'b h l c -> b h (l c)')
flat_pad = torch.zeros((b, h, l - 1), **dd)
flat_x_padded = torch.cat((flat_x, flat_pad), dim=2)
final_x = flat_x_padded.reshape(b, h, l + 1, 2 * l - 1)
final_x = final_x[:, :, :l, (l - 1):]
return final_x
def rel_pos_emb_1d(q, rel_emb, shared_heads):
"""
Same functionality as RelPosEmb1D
Args:
q: a 4d tensor of shape [batch, heads, tokens, dim]
rel_emb: a 2D or 3D tensor
of shape [ 2*tokens-1 , dim] or [ heads, 2*tokens-1 , dim]
"""
if shared_heads:
emb = torch.einsum('b h t d, r d -> b h t r', q, rel_emb)
else:
emb = torch.einsum('b h t d, h r d -> b h t r', q, rel_emb)
return relative_to_absolute(emb)
class RelPosEmb1DAISummer(nn.Module):
def __init__(self, tokens, dim_head, heads=None):
"""
Output: [batch head tokens tokens]
Args:
tokens: the number of the tokens of the seq
dim_head: the size of the last dimension of q
heads: if None representation is shared across heads.
else the number of heads must be provided
"""
super().__init__()
scale = dim_head ** -0.5
self.shared_heads = heads if heads is not None else True
if self.shared_heads:
self.rel_pos_emb = nn.Parameter(torch.randn(2 * tokens - 1, dim_head) * scale)
else:
self.rel_pos_emb = nn.Parameter(torch.randn(heads, 2 * tokens - 1, dim_head) * scale)
def forward(self, q):
return rel_pos_emb_1d(q, self.rel_pos_emb, self.shared_heads)
可以看到:
RelPosEmb1DAISummer初始化了 E r E^r Errel_pos_emb_1d为relative_to_absolute提供 Q E r ⊤ Q{E^{r}}^{\top} QEr⊤(为了便于书写,我们将其设为 S S S),通过在relative_to_absolute中各种形变和padding,从而得到了 S r e l S^{rel} Srel
理解的难点在relative_to_absolute中的实现过程。
这里会把 S S S从一个 ( N , 2 N − 1 ) (N, 2N-1) (N,2N−1)tensor转化为一个 ( N , N ) (N, N) (N,N)的tensor。这个过程实际上就是一个从表中查找的过程。
这里的实现其实有些晦涩,直接阅读代码是很难明白其中的意义。接下来会重点说这个。
需要注意的是,下面的分析都是按照1D的token序列来解释的,实际上2D的也是将H和W分别基于1D的策略处理的。也就是将H或者W合并到头索引那一维度,即这里的heads,结果就和1D的一致了,只是还会多一个额外的广播的过程。如下代码:
import torch.nn as nn
from einops import rearrange
from self_attention_cv.pos_embeddings.relative_embeddings_1D import RelPosEmb1D
class RelPosEmb2DAISummer(nn.Module):
def __init__(self, feat_map_size, dim_head, heads=None):
"""
Based on Bottleneck transformer paper
paper: https://arxiv.org/abs/2101.11605 . Figure 4
Output: qr^T [batch head tokens tokens]
Args:
tokens: the number of the tokens of the seq
dim_head: the size of the last dimension of q
heads: if None representation is shared across heads.
else the number of heads must be provided
"""
super().__init__()
self.h, self.w = feat_map_size # height , width
self.total_tokens = self.h * self.w
self.shared_heads = heads if heads is not None else True
self.emb_w = RelPosEmb1D(self.h, dim_head, heads)
self.emb_h = RelPosEmb1D(self.w, dim_head, heads)
def expand_emb(self, r, dim_size):
# Decompose and unsqueeze dimension
r = rearrange(r, 'b (h x) i j -> b h x () i j', x=dim_size)
expand_index = [-1, -1, -1, dim_size, -1, -1] # -1 indicates no expansion
r = r.expand(expand_index)
return rearrange(r, 'b h x1 x2 y1 y2 -> b h (x1 y1) (x2 y2)')
def forward(self, q):
"""
Args:
q: [batch, heads, tokens, dim_head]
Returns: [ batch, heads, tokens, tokens]
"""
assert self.total_tokens == q.shape[2], f'Tokens {q.shape[2]} of q must \
be equal to the product of the feat map size {self.total_tokens} '
# out: [batch head*w h h]
r_h = self.emb_w(rearrange(q, 'b h (x y) d -> b (h x) y d', x=self.h, y=self.w))
r_w = self.emb_h(rearrange(q, 'b h (x y) d -> b (h y) x d', x=self.h, y=self.w))
q_r = self.expand_emb(r_h, self.h) + self.expand_emb(r_w, self.w)
return q_r
提前的思考
首先我们要明确,为什么对于每个维度为 d d d的token T i T_i Ti,其对应的整体 S S S会有 2 N − 1 → N 2N-1 \rightarrow N 2N−1→N这样一个缩减的过程?
因为对于长为 N N N的序列中的每一个元素 T i T_i Ti,实际上与之可能有关的元素 T j T_j Tj最多只有 N N N个(废话,O(∩_∩)O哈哈~)。
所以对于每个元素,实际上这里的 S S S并不会都用到。这里的 S S S只是所有可能会用到的情形(分别对应于各种相对距离 j − i ∈ { − N + 1 , − N + 2 , ⋯ , − 1 , 0 , 1 , ⋯ , N − 2 , N − 1 } j-i \in \{-N+1, -N+2, \cdots, -1, 0, 1, \cdots, N-2, N-1\} j−i∈{−N+1,−N+2,⋯,−1,0,1,⋯,N−2,N−1})。
这里需要说明的一点是,有些相对注意力的策略中,会使用固定的窗口。
即对于窗口之外的j,和窗口边界上的j的相对距离认为是一样的,即 c l i p ( j − i , − k , k ) clip(j-i, -k, k) clip(j−i,−k,k),我们这里介绍的可以看做是 k = N − 1 k=N-1 k=N−1。
例如这个实现:https://github.com/TensorUI/relative-position-pytorch/blob/master/relative_position.py
所以这里前面展示的这个函数relative_to_absolute实际上就是在做这样一件事:从 S S S中抽取对应于各个token T i T_i Ti真实存在的相对距离 j − i j-i j−i的位置嵌入集合 { S i , r e l 2 b s ( j − i ) } j c l i p ( j − i , − N + 1 , N − 1 ) \{ S_{i, rel2bs(j-i)} \}^{clip(j-i, -N+1,N-1)}_{j} {Si,rel2bs(j−i)}jclip(j−i,−N+1,N−1)来得到最终的 S r e l S^{rel} Srel。
背后的动机
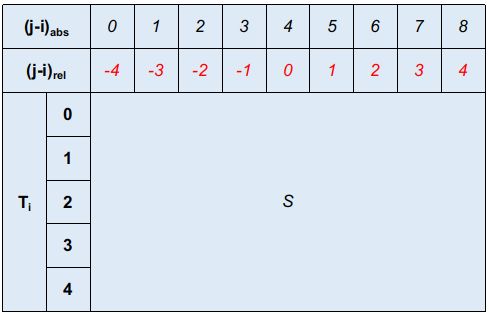
为了便于展示这个代码描述的过程的动机,我们首先构造一个简单的序列 { a , b , c , d , e } \{ a, b, c, d, e \} {a,b,c,d,e},包含5个元素,则 N = 5 N=5 N=5。这里嵌入的维度为 d d d。则位置 i & j i\&j i&j对应的相对距离矩阵可以表示为:
图1
这里红色标记表示各个位置上的相对距离。
我们再看下假定已经得到的 S ∈ R N × ( 2 N − 1 ) S \in \mathbb{R}^{N \times (2N-1)} S∈RN×(2N−1):
图2
这里对各个 T i T_i Ti都提供了独立的一套嵌入 S i ∈ R 2 N − 1 S_i \in \mathbb{R}^{2N-1} Si∈R2N−1。为了直观的展示,这里我们也展示了对于这 2 N − 1 2N-1 2N−1个相对位置的相对距离,同时也标注了对应于嵌入矩阵各列的绝对索引。
接下来我们就需要提取想要的那部分嵌入的tensor了。
这个时候,我们需要明白,我们要获取的是哪部分结果:
图3
这里实际上就是结合了图1中已经得到的相对距离和图2中的 ( j − i ) r e l (j-i)_{rel} (j−i)rel,从而就可以明白,红色的这部分区域正是我们想要的那部分合理索引对应的位置编码。
稍微整理下,也就是如下的绝对索引对应的嵌入信息 S r e l ∈ R N × N S^{rel} \in \mathbb{R}^{N \times N} Srel∈RN×N(形状与 Q K ⊤ QK^\top QK⊤一致,可以直接元素级相加):
图4
而前面的代码relative_to_absolute正是在做这样一件事。就是通过不断的padding和reshape来从图3中获得图4中这些绝对索引对应的嵌入。
对应的流程
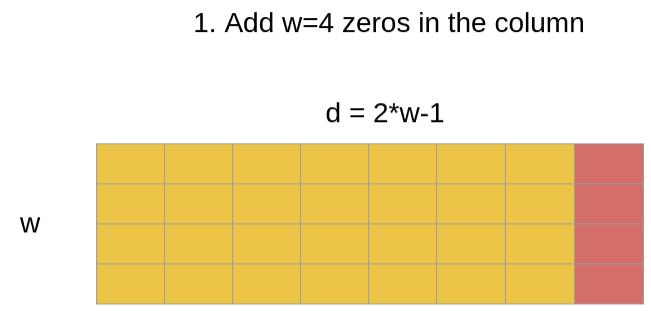
关于代码的流程,参考链接中的图例非常直观:
col_pad = torch.zeros((b, h, l, 1), **dd)
x = torch.cat((q, col_pad), dim=3) # zero pad 2l-1 to 2l
flat_x = rearrange(x, 'b h l c -> b h (l c)')
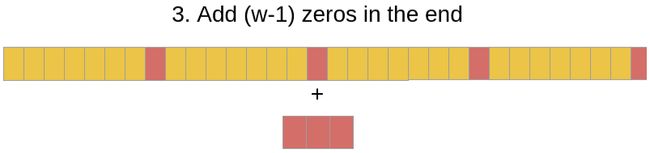
flat_pad = torch.zeros((b, h, l - 1), **dd)
flat_x_padded = torch.cat((flat_x, flat_pad), dim=2)
final_x = flat_x_padded.reshape(b, h, l + 1, 2 * l - 1)
final_x = final_x[:, :, :l, (l - 1):]
将提取的内容对应于原始的 R R R中,可以看到是如下区域,正如前面的分析所示。