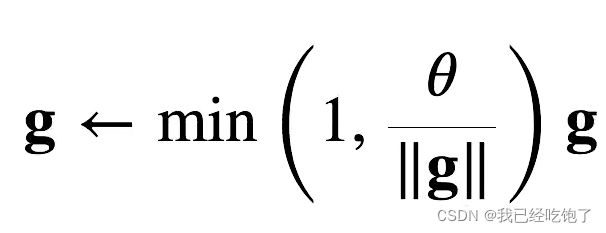【动手学习pytorch笔记】22.RNN从零实现
RNN从零实现
%matplotlib inline
import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
上一节的函数
load_data_time_machine,传入两个参数batch_size:批量大小
num_steps:时间步(窗口大小,即根据前面多少个词做预测)
one-hot编码
F.one_hot(torch.tensor([0, 2]), len(vocab))
one-hot编码,把任意向量表示成长度为len(vocab)的编码,我们使用的是’char’构建的词典,长度为28
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0]])
那么对于我们的输入x来说,以下面这个为例 X (batchsize = 2, num_steps = 5)
X:
[[0, 1, 2, 3, 4] [5, 6, 7, 8, 9]]
X = torch.arange(10).reshape((2, 5))
F.one_hot(X.T, 28).shape
输出
torch.Size([5, 2, 28])
这里为什么要把X取转置呢?
拿本例来说,我们的输入是一个 2 * 5 * 28的矩阵。batchsize = 2 可以理解为有几句话,timestep = 5 可以理解为有几个词,vocab_size = 28
再进入rnn这个函数里面看
如果不转置(首先我们先忽略H0是一个2 * 28的矩阵)
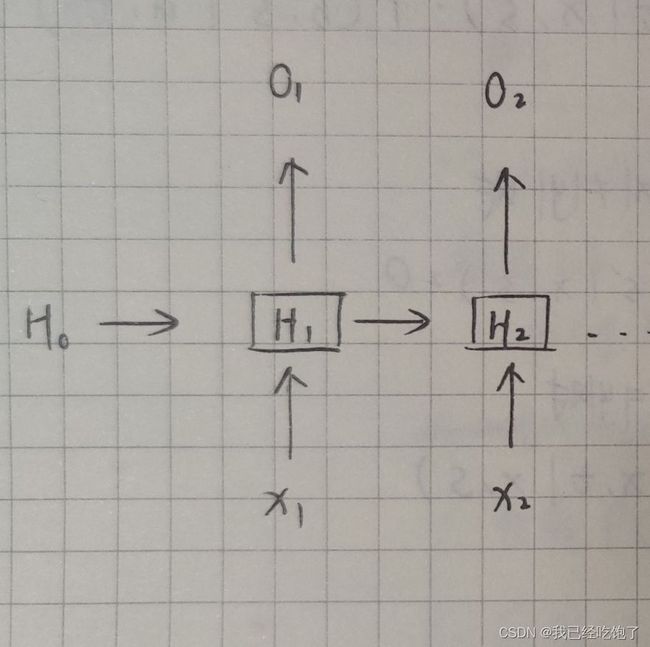
[ 5 * 28 ] 点乘[ 28 * 28 ] + H 0 H_0 H0 * W h h W_{hh} Whh = H 1 H_1 H1,我们可以看到这个H1记录的是第一句话的信息,但是第一句话和第二句话是独立的,这个和我们的需求是违背的。我们的需求是,拿一句话的第n个词预测以及第n个词之前的历史信息,预测n+1个词。
如果转置 2 * 28,那记录的就是词于词的关系而不是句子与句子的关系了
初始化模型参数
def get_params(vocab_size, num_hiddens, device):
# 输入一个词的one-hot编码 = vocab_size
# 输出是vocab_size大小的分类问题 = vocab_size
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
# 隐藏层参数
W_xh = normal((num_inputs, num_hiddens))
W_hh = normal((num_hiddens, num_hiddens))
b_h = torch.zeros(num_hiddens, device=device)
# 输出层参数
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
对模型的可学习参数进行初始化
首先我们回忆一下RNN
H t = σ ( x t W x h + H t − 1 W h h + b n ) H_t = \sigma(x_tW_{xh} + H_{t-1}W_{hh} +b_n) Ht=σ(xtWxh+Ht−1Whh+bn)
O t = H t W h q + b q O_t = H_tW_{hq}+b_q Ot=HtWhq+bq
即当前的隐藏状态由当前输出和上一个隐藏状态决定
各个维度:
x t x_t xt: 2 * 28
W x h W_{xh} Wxh: 28 * num_hiddens
W h h W_{hh} Whh: num_hiddens * num_hiddens
W h q W_{hq} Whq: num_hiddens * 28
H t − 1 H_{t-1} Ht−1: batchsize * num_hiddens
b n b_n bn: num_hiddens 大小的标量
初始化隐藏状态
def init_rnn_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device), )
大小 = batchsize * num_hiddens
另外要注意的是:return
(torch.zeros((batch_size, num_hiddens), device=device),)我们把隐藏状态放进了一个tuple中(虽然在RNN中只有一个张量,但之后LSTM中会有两个,个人理解:隐藏状态自始至终都只有一个)
rnn函数定义了如何在一个时间步内计算隐藏状态和输出(正向传播过程和MLP中的forward()类似)
def rnn(inputs, state, params):
# inputs的形状:(时间步数量,批量大小,词表大小)
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
# X的形状:(批量大小,词表大小)
for X in inputs:
H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
Y = torch.mm(H, W_hq) + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
inputs: 时间步 * 批次大小 * 词典长度
for X in inputs:在0维度上进行遍历for循环中的两个H并不是同一个,
torch.mm(H, W_hh)中的H是上一个时间步的隐藏状态,等号左边的H才是当前时间步的隐藏状态然后将输出加入List,
outputs.append(Y),这时候Y是 时间步 * 批次大小 * 词典长度的矩阵而该函数最后输出的Y在第0为维度进行了拼接
变成了:行数 = 时间步 * 批次大小
列数 = 词典长度
同时还返回了隐藏状态
定义一个类封装上面的函数
class RNNModelScratch: #@save
"""从零开始实现的循环神经网络模型"""
def __init__(self, vocab_size, num_hiddens, device,
get_params, init_state, forward_fn):
self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
self.params = get_params(vocab_size, num_hiddens, device)
self.init_state, self.forward_fn = init_state, forward_fn
def __call__(self, X, state):
X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
return self.forward_fn(X, state, self.params)
def begin_state(self, batch_size, device):
return self.init_state(batch_size, self.num_hiddens, device)
验证一下输出是否是正确的形状
num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
Y.shape, len(new_state), new_state[0].shape
输出
(torch.Size([10, 28]), 1, torch.Size([2, 512]))
这里输入的X是 2 * 5 的
Y被拼接了 5 * 2 = 10
预测
接下来我们先看预测,再看训练
def predict_ch8(prefix, num_preds, net, vocab, device): #@save
"""在prefix后面生成新字符"""
state = net.begin_state(batch_size=1, device=device)
outputs = [vocab[prefix[0]]]
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
for y in prefix[1:]: # 预热期
_, state = net(get_input(), state)
outputs.append(vocab[y])
for _ in range(num_preds): # 预测num_preds步
y, state = net(get_input(), state)
outputs.append(int(y.argmax(dim=1).reshape(1)))
return ''.join([vocab.idx_to_token[i] for i in outputs])
(prefix, num_preds, net, vocab, device)prefix::输入的字符串,
num_preds:预测接下来几个词
net:训练好的网络
vocab:便于把索引转换成字符串,查看输出
state = net.begin_state(batch_size=1, device=device)首先获取初始隐藏状态,因为是我们是在做预测,所以 batch_size = 1
outputs = [vocab[prefix[0]]]这时候我们把输入字符串的第一个词放进 outputs ,因为我们接下来获取输入
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))是从outputs 中获取最新预测的值作为下一次的输入。而第一个词是没法被预测的,所以我们先放进去
for y in prefix[1:]: # 预热期 _, state = net(get_input(), state) outputs.append(vocab[y])第一个已经放进去了,再把之后的也放到 outputs,这里我们并不是一个接一个作为输出,因为我们已经有准确的值了,那这个for循环的意义是啥?是为了更新隐藏状态state,
个人理解:隐藏状态自始至终都只有一个体会一下这句话!for _ in range(num_preds): # 预测num_preds步 y, state = net(get_input(), state) outputs.append(int(y.argmax(dim=1).reshape(1)))这个for循环,就是我们要自己做预测了,
outputs.append(int(y.argmax(dim=1).reshape(1)))把 y 中最大的索引取出来加入outputs中
return ''.join([vocab.idx_to_token[i] for i in outputs])最后用 vocab 转换成字符输出除去
测试一下,输入’time traveller ’
predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu())
输出
'time traveller xbzp xbzp '
能看到对于一个没有经过训练的网络,它输出了 ‘xbzp’
梯度裁剪
对于RNN来说,回忆上面的公式
H t = σ ( x t W x h + H t − 1 W h h + b n ) H_t = \sigma(x_tW_{xh} + H_{t-1}W_{hh} +b_n) Ht=σ(xtWxh+Ht−1Whh+bn)
O t = H t W h q + b q O_t = H_tW_{hq}+b_q Ot=HtWhq+bq
就算我只用了单隐藏层的MLP,但是因为时间步的传递,也相当于我做了很多层,所以很容易就梯度爆炸了
所以,进行梯度裁剪
def grad_clipping(net, theta): #@save
"""裁剪梯度"""
if isinstance(net, nn.Module):
params = [p for p in net.parameters() if p.requires_grad]
else:
params = net.params
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > theta:
for param in params:
param.grad[:] *= theta / norm
把整个网络中所有的参数拿出来,并不是某一个时间步,是所有
对其求norm
可以print一下看看p的大小
for p in params: print(p.shape)
输出torch.Size([28, 512]) W x h W_{xh} Wxh
torch.Size([512, 512]) W h h W_{hh} Whh
torch.Size([512]) b n b_n bn
torch.Size([512, 28]) W h q W_{hq} Whq
torch.Size([28]) b q b_q bq对所有梯度的求平方和(一个时间步上的?),之后再求和?不太理解,是再对所有的时间步再求个和吧
训练
定义一次迭代周期内的训练模型
#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
"""训练网络一个迭代周期(定义见第8章)"""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # 训练损失之和,词元数量
for X, Y in train_iter:
# 初始化隐藏状态,注意如果是use_random_iter,那么每一个batch都要将state初始化为0,因为前面时间步的信息和当前时间步的信息没有关系
if state is None or use_random_iter:
# 在第一次迭代或使用随机抽样时初始化state
state = net.begin_state(batch_size=X.shape[0], device=device)
else:
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# state对于nn.GRU是个张量
state.detach_()
else:
# state对于nn.LSTM或对于我们从零开始实现的模型是个张量
for s in state:
s.detach_()
y = Y.T.reshape(-1)
X, y = X.to(device), y.to(device)
y_hat, state = net(X, state)
l = loss(y_hat, y.long()).mean()
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad()
l.backward()
grad_clipping(net, 1)
updater.step()
else:
l.backward()
grad_clipping(net, 1)
# 因为已经调用了mean函数
updater(batch_size=1)
metric.add(l * y.numel(), y.numel())
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
use_random_iter:会导致隐藏状态更新不一样回忆一下,如果是随机的,则下一个batch和上一个batch的第i个输入没有关系
如果不是随机的,则下一个batch和上一个batch的第i个输入是连着的
训练
#@save
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
use_random_iter=False):
"""训练模型(定义见第8章)"""
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs])
# 初始化
if isinstance(net, nn.Module):
updater = torch.optim.SGD(net.parameters(), lr)
else:
updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
# 训练和预测
for epoch in range(num_epochs):
ppl, speed = train_epoch_ch8(
net, train_iter, loss, updater, device, use_random_iter)
if (epoch + 1) % 10 == 0:
print(predict('time traveller'))
animator.add(epoch + 1, [ppl])
print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
print(predict('time traveller'))
print(predict('traveller'))
num_epochs, lr = 500, 1
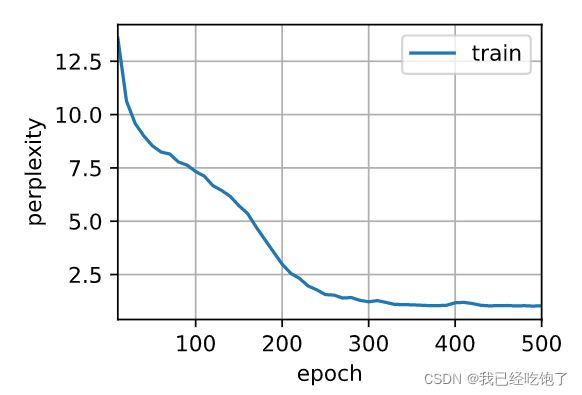
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())
困惑度 1.0, 64157.7 词元/秒 cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
init_rnn_state, rnn)
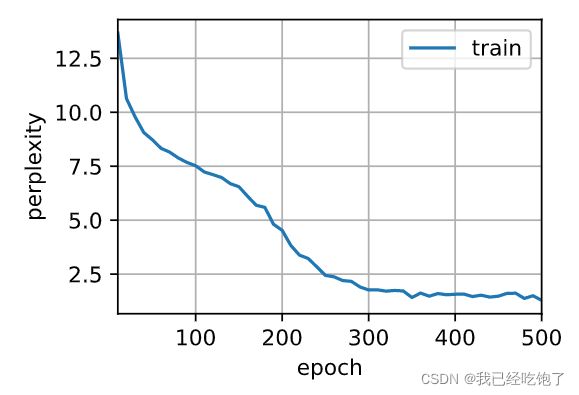
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),
use_random_iter=True)
困惑度 1.5, 64642.5 词元/秒 cuda:0
time travellerit s against reason said filby and whyecanditwivk
travellerit s against reason said filby and whyecanditwivk