【0基础百日刷题】洛谷刷题知识拾遗

刷题得意义：
有时候会发现一个简单的题目总是通不过测试，调试一次 就能找出一处bug。这都是我们编程时对逻辑的思考不充分而导致的失误。

1. 刷题就是为了找出我们自己常犯的错误，总结归纳后，在以后避免出现错误。
2. 学习体会算法优化，减少代码复杂度。
3. 见识到大佬的写法，拓展自己的知识面

一.洛谷刷题得

1.P1420差分数组

我们先看一下题目描述

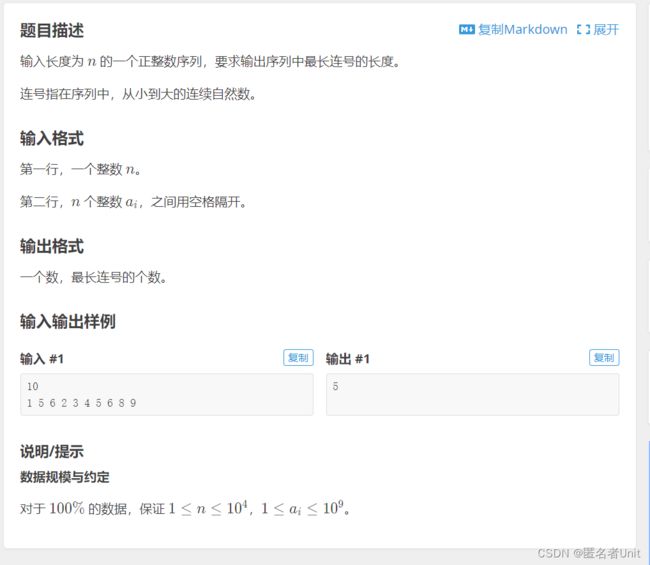
分析：题目要求两行输入，第一行输入的n是第二行数字的个数。而我们需要输出n个数中，连号个数的最大值。
eg：1 2 3 8 9 5 6 7 8 9则输出5.
避坑要点：
1.输出的是连号的最大值，所以可能有多个连号，并且有大小之分，所以不能单单只用一个一次连号的计数器。
2.计算连号的个数时，比如

int count = 0;
if((ch[i]+1)==ch[i+1])
{
	count++;	
}

我们仔细一想就可以发现计数器的值小了1，所以我们在定义count时将它初始化为1，才合情合理。
拓展知识解法：我们将输入的n个数存入数组后.连号也就是元素加一等于下一个元素的值，这里我们就可在定义一个数组也就是差分数组，

int main() 
{
	int a[100001], d[100001];
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) 
	{
		scanf("%d", &a[i]);
		d[i] = a[i] - a[i - 1];
	}

数组d[i]的元素就是a[i]减去上一个元素的差值，如果数组元素较大 并且要进行频繁的区间操作时，常会用到差分数组牺牲内存，换取时间上的高效。
我们还需要创建两个变量一个用来计数连号的个数，一个用来接受最大值，逻辑理明，代码奉上，大家仔细体会。

#include  
 
int a[100000], d[100000];
int main() 
{
	int n, num = 1, count = 0;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) 
	{
		scanf("%d", &a[i]);
		d[i] = a[i] - a[i - 1];
	}
	for (int i = 1; i <= n+1; i++) 
	{
		if (d[i] == 1) 
			count++;
		if (d[i] != 1) 
		{
			if (count > num) num = count;
			count = 0;
		}
	}
	if (num > 1) 
		printf("%d", num+1);
	else 
		printf("1");
	return 0; 
}

2.P2669数列求和

先看一下题目描述

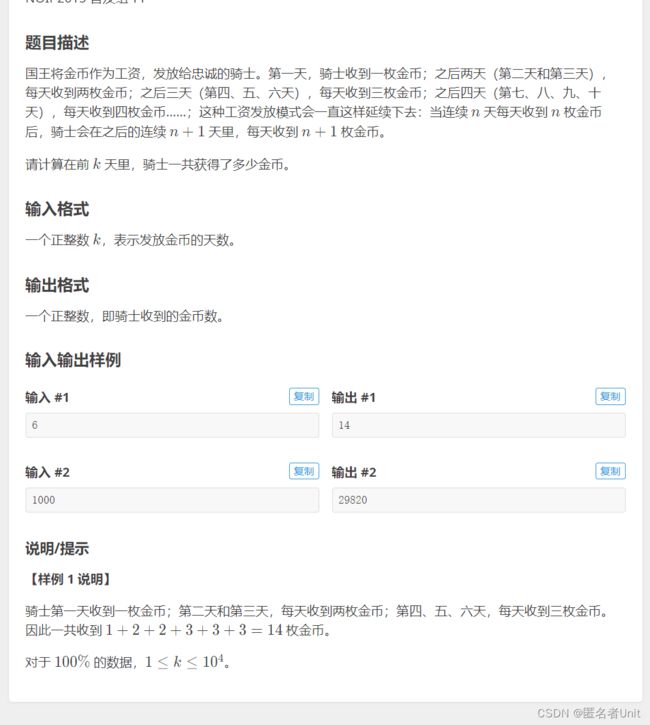
分析：我们可以将收到相同金币的天数看为一个数列的项 比如收到1金币 2金币 3金币 …天数看成等差数列就是：1 2 3 4 5 6 7 8 9 …

不管k在n的左端还是右端，我们先判断k的值在哪个n中

int the_world(int k)
{
	int n = 1;
	while (1)
	{
		if (n * (n + 1) / 2 >= k)
		{
			return n;
		}
		n++;
	}
}

int main()
{
	int i, k, n;
	int sum = 0;
	scanf("%d", &k);
	n = the_world(k);

	return 0;
}

算出n值后我们接着讲金币数算出：

	for (i = 1; i <= n; i++)
	{
		sum += i * i;
	}
	sum += n * (k - n * (n + 1) / 2);

我们先用一个for循环算出n的天数下的总金币数，又因为k不一定在n天数中的最右端，所以我们还要减去n * (k - n * (n + 1) / 2) n代表金币数，k减去n求和可以算出相差的天数。最后将sum打印出来就可以AC这题了。

3.P1307数字反转

避坑要点：我们将输入的数组作为字符存进数组，如果直接倒序打印的话，会出现一下错误


所以我们需要注意负号和0的处理。
我们想到如果输入的是负数的话，我们就先将负号打印出来。

	if (ch[0] == '-')
	{
		printf("-");
	}

那对于0我们应该怎么处理呢？这里有一种巧妙的思路，可以学习一下
我们对输入的字符倒序检测，如果是0则继续，知道检测到数组第一个非0数，将此时的循环数i保留下来，在下面的遍历打印中，不初始化i，直接使用保留下来的i

下面完整代码奉上：

#include 
#include 



int main()
{
	char ch[11];
	int n=0;
	gets(ch);
	int len = strlen(ch);
	if (ch[0] == '-')
	{
		printf("-");
	}
	int i = 0;
	for (i=len-1;i>=1;i--)
	{
		if (ch[i] != '0')
			break;
	}
	for (; i >= 0; i--)
	{
		if (ch[i] != '-')
		{
			printf("%c", ch[i]);
		}
	}		
	return 0;
}

4.P5725三角形

我们再来看一下这一题：

分析：打印矩形没啥难度，需要注意的是需要补0的输出格式，这里我们要了解：

---

---

---

	int n;
	scanf("%d", &n);
	int i = 1;
	int j = 1;
	int m = n;
	while (m!=0)
	{
		for (; i <= n; i++)
		{
			for (; j <=i*n; j++)
			{
				printf("%02d", j);
			}
			printf("\n");
			m--;
		}
	}

看看效果：
问题在于如何将这个三角形打印出来

---

我们想这个三角形真是奇怪 ，， 如果要求的是这样的：
那我轻松可以实现：

#include 

int main()
{
	int n = 0;
	int j = 1;
	int k = 1;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{

		for (k = 1; k <= i; k++)
		{
			printf("%02d", j++);
		}
		printf("\n");
	}
	return 0;
}

而题目要求的三角形
可以观察出在打印每一行数之前，需要先打印n-行数个空格，
代码奉上：

#include 

int main()
{
	int n;
	scanf("%d", &n);
	int i = 1;
	int j = 1;
	int m = n;
	while (m!=0)
	{
		for (; i <= n; i++)
		{
			for (; j <=i*n; j++)
			{
				printf("%02d", j);
			}
			printf("\n");
			m--;
		}
	}
	int k = 1;

	int c = 1;
	printf("\n");
	for (i=0;i<n;i++)
	{
		for (j = n-i-1; j >0; j--)
		{
			printf("  ");
		}
		for (k = i + 1; k > 0; k--)
		{
			printf("%02d", c);
			c++;
		}
		printf("\n");

	}
	return 0;
}

5.P1980计数问题

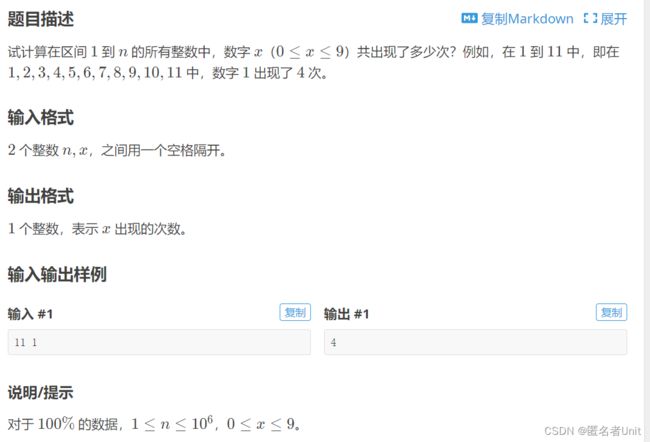分析：根据题目描述，我们需要遍历从1到n的数并判断某个数 出现的次数，这里我们就需用到%10/10来判断一个数的每一位。此方法基本框架是：

while (tmp)
	{
		if (tmp % 10 == x)
		{
			count++;
		}
		tmp /= 10;
	}	

%10可以拿出某个数的个位，/10可以将此数的个位拿下去。
我们可以解出此题：

#include 

int main()
{
	int n,x;
	scanf("%d %d", &n, &x);
	int count = 0;
	int i = 0;
	for (i = 1; i <= n; i++)
	{
		int tmp = i;
		while (tmp)
		{
			if (tmp % 10 == x)
			{
				count++;
			}
			tmp /= 10;
		}	
	}
	printf("%d", count);
	return 0;
}

避坑要点：我使用了tmp代替了i，是防止while循环和判断改变i的值，影响for循环的进行，从而出现错误。

6.P1217回文质数

我们根据题目要求和提示，先写遍历和判断逻辑：

#include 
#include 

int main()
{
	int a, b;
	scanf("%d %d", &a, &b);
	int i = 0;
	for (i = a; i <= b; i++)
	{
		if ((is_hui(i)) && (is_form(i)))
		{
			printf("%d\n", i);
		}
	}
	return 0;
}

然后再分别编写回文数和素数的函数：

int is_form(int i)
{
	int j = 0;
	for (j = 2; j<=sqrt(i); j++)
	{
		if (i % j == 0)
			return 0;
	}
	return 1;
}

int is_hui(int i)
{
	int k = 0;
	int tmp = i;
	while (i != 0)
	{
		k = i % 10 + k * 10;
		i /= 10;
	}
	if (k == tmp)
	{
		return 1;
	}
	else
		return 0;
}

k = i % 10 + k * 10可以将i的每一位保留下来并且倒序储存，是个技巧 。 但是两个函数写完后 我们提交洛谷时会发现有超时的监测点，
这里有个小知识点，一亿之内最大的回文数是9989899，我们对遍历条件可以进行优化：

int main()
{
	int a, b;
	scanf("%d %d", &a, &b);
	int i = 0;
	if (b > 10000000)
	{
		b = 10000000;
	}
	for (i = a; i <= b; i++)
	{
		if ((is_hui(i)) && (is_form(i)))
		{
			printf("%d\n", i);
		}
	}
	return 0;
}

再次提交，就可以通过了！

如果调试一个程序让你很苦恼，千万不要放弃，成功永远在拐角之后，除非你走到拐角，否则你永远不知道你离他多远，所以，请记住，坚持不懈，直到成功。