由一个熵不等式引发的数学调研
1. OT 中的熵不等式
在阅读最优传输 ( O p t i m a l T r a n s p o r t , O T ) (Optimal Transport, OT) (OptimalTransport,OT) 论文 Sinkhorn Distances: Lightspeed Computation of Optimal Transport 时,碰到关于联合概率分布的熵的不等式 ∀ r , c ∈ Σ d , ∀ P ∈ U ( r , c ) , h ( P ) ≤ h ( r ) + h ( c ) (1) \forall \bm{r}, \bm{c} \in Σ_d, \forall P \in U(\bm{r}, \bm{c}), h(P) ≤ h(\bm{r}) + h(\bm{c}) \tag{1} ∀r,c∈Σd,∀P∈U(r,c),h(P)≤h(r)+h(c)(1) 其中 Σ d : = { x ∈ R + d ∣ x ⊺ 1 d = 1 } Σ_d := \{\bm{x} \in \mathbb{R}_+^d | \bm{x}^\intercal \bm{1}_d = 1\} Σd:={x∈R+d∣x⊺1d=1},即概率单纯形, U ( r , c ) = { P ∈ R + d × d ∣ P 1 d = r , P ⊺ 1 d = c } U(\bm{r}, \bm{c}) = \{P \in \mathbb{R}_+^{d \times d} | P \bm{1}_d = \bm{r}, P^\intercal \bm{1}_d = \bm{c}\} U(r,c)={P∈R+d×d∣P1d=r,P⊺1d=c} 是 r \bm{r} r 和 c \bm{c} c 的联合概率分布集合。乍一看,不知道为什么,怎么去证明?首先想到求 h ( P ) h(P) h(P) 的最大值,如果其最大值就是 h ( r ) + h ( c ) h(\bm{r}) + h(\bm{c}) h(r)+h(c),那么就证明了不等式。不过这比较麻烦,需要求导、解大串方程等,望而却步。查阅一些博客也没有证明这个不等式的。
1.1 均匀分布熵最大
原文中还有个等式 h ( r c ⊺ ) = h ( r ) + h ( c ) (2) h(\bm{r}\bm{c}^\intercal) = h(\bm{r}) + h(\bm{c}) \tag{2} h(rc⊺)=h(r)+h(c)(2) 这个很简单,下面进行推导。先看熵的计算公式: h ( p ) = − ∑ i p i l o g p i (3) h(\bm{p}) = -\sum_i p_i log p_i \tag{3} h(p)=−i∑pilogpi(3) 其中 p i p_i pi 为事件 i i i 的概率。那么 h ( r c ⊺ ) = − ∑ i , j r i c j l o g ( r i c j ) = − ∑ i , j r i c j ( l o g ( r i ) + l o g ( c j ) ) = − ∑ i , j r i c j l o g ( r i ) − ∑ i , j r i c j l o g ( c j ) = − ∑ i r i l o g ( r i ) − ∑ j c j l o g ( c j ) = h ( r ) + h ( c ) \begin{aligned} h(\bm{r}\bm{c}^\intercal) &= -\sum_{i,j} {r_i c_j} log(r_i c_j) \\ &= -\sum_{i,j} {r_i c_j} (log(r_i) + log(c_j)) \\ &= -\sum_{i,j} {r_i c_j} log(r_i) - \sum_{i,j} {r_i c_j} log(c_j) \\ &= -\sum_{i} {r_i} log(r_i) - \sum_{j} {c_j} log(c_j) \\ &= h(\bm{r}) + h(\bm{c}) \end{aligned} h(rc⊺)=−i,j∑ricjlog(ricj)=−i,j∑ricj(log(ri)+log(cj))=−i,j∑ricjlog(ri)−i,j∑ricjlog(cj)=−i∑rilog(ri)−j∑cjlog(cj)=h(r)+h(c) 这么一看,不等式就变成了 h ( P ) ≤ h ( r c ⊺ ) h(P) ≤ h(\bm{r}\bm{c}^\intercal) h(P)≤h(rc⊺),也就是说,当联合概率分布 P = r c ⊺ P = \bm{r}\bm{c}^\intercal P=rc⊺ 时,熵最大。如何证明呢?我只能从直觉上感到, P = r c ⊺ P = \bm{r}\bm{c}^\intercal P=rc⊺ 是边缘概率为 r \bm{r} r 和 c \bm{c} c 时最均匀的联合概率分布。
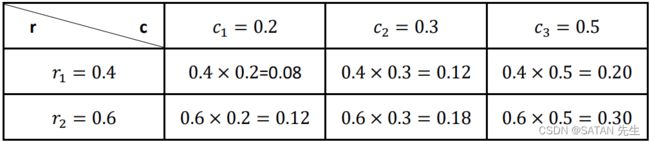
看上面的例子,按运输货物的说法, r 1 = 0.4 r_1=0.4 r1=0.4 的货物要运送到目的地 c 1 , c 2 , c 3 c_1,c_2,c_3 c1,c2,c3,按照三个目的地的需求量 0.2 , 0.3 , 0.5 0.2, 0.3, 0.5 0.2,0.3,0.5 均匀地分配就是 r 1 c 1 = 0.08 , r 1 c 2 = 0.12 , r 1 c 3 = 0.20 r_1c_1=0.08, r_1c_2=0.12, r_1c_3=0.20 r1c1=0.08,r1c2=0.12,r1c3=0.20, r 2 r_2 r2 的运送也是同理。是不是均匀分布时熵最大?
证明均匀分布熵最大
既然如此,那就证明一下:均匀分布下随机变量的熵最大。联合概率分布这个比较麻烦,所以先尝试求一个随机变量下的熵最大值。设有一个离散随机变量 X X X,可取值为 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn,概率分布为 p 1 , p 2 , . . . , p n p_1, p_2, ..., p_n p1,p2,...,pn,当 n = 2 n=2 n=2 时, h ( p ) = − p 1 l o g p 1 − p 2 l o g p 2 h(\bm{p}) = -p_1log p_1 - p_2 log p_2 h(p)=−p1logp1−p2logp2,设 p 1 = x p_1 = x p1=x,则 h ( p ) = f ( x ) = − x l o g x − ( 1 − x ) l o g ( 1 − x ) (4) h(\bm{p}) = f(x) = -xlogx - (1-x)log(1-x) \tag{4} h(p)=f(x)=−xlogx−(1−x)log(1−x)(4) 这个函数很简单,求导 f ′ ( x ) = l o g 1 − x x = 0 f^{'}(x) = log\frac{1-x}{x} = 0 f′(x)=logx1−x=0,可得 x = 0.5 x = 0.5 x=0.5,且 f ′ ′ ( x ) = − ( 1 1 − x + 1 x ) < 0 f^{''}(x) = -(\frac{1}{1-x} + \frac{1}{x}) < 0 f′′(x)=−(1−x1+x1)<0, f ( x ) f(x) f(x) 为凹函数,故 p 1 = x = 0.5 p_1 = x = 0.5 p1=x=0.5 时, h ( p ) h(\bm{p}) h(p) 最大,下面归纳法证明 n 为任意大于 2 的整数时,均匀分布熵最大:
设 n n n 个事件时,均匀分布熵最大,即 p ( x i ) = 1 / n p(x_i) = 1/n p(xi)=1/n,则只需证明: n + 1 n+1 n+1 个事件时,均匀分布 p ( x i ) = 1 / ( n + 1 ) p(x_i) = 1/(n+1) p(xi)=1/(n+1) 时熵最大。
取出 1 个事件,不妨取出 x n + 1 x_{n+1} xn+1,令 p ( x n + 1 ) = x p(x_{n+1}) = x p(xn+1)=x,其他事件的总概率为 ∑ i n p ( x i ) = 1 − x \sum_i^np(x_i) = 1-x ∑inp(xi)=1−x,为使这 n n n 个事件( x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn)的平均信息量最大,则均匀分布:每个事件的概率为 p ( x i ) = 1 − x n p(x_i) = \frac{1-x}{n} p(xi)=n1−x, i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n,则 h ( p ) = f ( x ) = − x l o g x + n ∗ ( − 1 − x n l o g 1 − x n ) = − x l o g x − ( 1 − x ) l o g 1 − x n \begin{aligned} h(\bm{p}) = f(x) &= -x logx + n * (-\frac{1-x}{n}log\frac{1-x}{n}) \\ &= -x logx - (1-x)log\frac{1-x}{n} \end{aligned} h(p)=f(x)=−xlogx+n∗(−n1−xlogn1−x)=−xlogx−(1−x)logn1−x 求导 f ′ ( x ) = l o g 1 − x n x = 0 f^{'}(x) = log\frac{1-x}{nx} = 0 f′(x)=lognx1−x=0,得 x = 1 n + 1 x = \frac{1}{n+1} x=n+11,即 p ( x n + 1 ) = 1 n + 1 p(x_{n+1}) = \frac{1}{n+1} p(xn+1)=n+11,其他事件的概率为 p ( x i ) = 1 − x n = 1 n + 1 p(x_i) = \frac{1-x}{n} = \frac{1}{n+1} p(xi)=n1−x=n+11,所以, n + 1 n+1 n+1 个事件时,均匀分布 p ( x i ) = 1 / ( n + 1 ) p(x_i) = 1/(n+1) p(xi)=1/(n+1) 熵最大。
【注】:这里有个疑问,抽取出 x n + 1 x_{n+1} xn+1 后,剩下的 ∑ i n p ( x i ) = 1 − x \sum_i^np(x_i) = 1-x ∑inp(xi)=1−x,总概率已经不是 1,“这 n n n 个事件均匀分布时熵最大” 是否还成立?
【答】:是成立的, ( 4 ) (4) (4) 中把 1 换成任意常数 a a a,都能得到 f ′ ( x ) = l o g a − x x = 0 f^{'}(x) = log\frac{a-x}{x} = 0 f′(x)=logxa−x=0,依然是均匀分布。
至此,完成了对 “对于一个随机变量,均匀分布时熵最大” 的证明。但是,联合分布 P P P 有边缘概率的条件限制,“均匀分布” r c ⊺ \bm{r}\bm{c}^\intercal rc⊺ 毕竟不是严格意义上的均匀分布,是有条件限制的,还不能确定 r c ⊺ \bm{r}\bm{c}^\intercal rc⊺ 就一定是熵最大的联合概率分布。
既然是有条件限制的,所以想到了拉格朗日乘数法求极值,查阅博客,在《熵的证明,为什么均匀分布熵最大》 一文中找到了相关证明,不过这依然是一个随机变量的情况,在这里我再表述一下:
令 f ( p , λ ) = h ( p ) + λ ( ∑ i p i − 1 ) = − ∑ i p i l o g p i + λ ( ∑ i p i − 1 ) \begin{aligned} f(\bm{p}, \lambda) &= h(\bm{p}) + \lambda(\sum_i p_i - 1) \\ &= -\sum_i p_i log p_i + \lambda(\sum_i p_i - 1) \end{aligned} f(p,λ)=h(p)+λ(i∑pi−1)=−i∑pilogpi+λ(i∑pi−1) 对 p \bm{p} p 和 λ \lambda λ 求导,得到 ∂ f ∂ p i = − ( 1 + l o g p i ) + λ = 0 ∂ f ∂ λ = ∑ i p i − 1 = 0 \begin{aligned} \frac{\partial f}{\partial p_i} &= -(1 + logp_i) + \lambda = 0 \\ \frac{\partial f}{\partial \lambda} &= \sum_i p_i - 1 = 0 \end{aligned} ∂pi∂f∂λ∂f=−(1+logpi)+λ=0=i∑pi−1=0 假设对数函数底为 e e e,得 p i = e λ − 1 p_i = e^{\lambda - 1} pi=eλ−1,所有的 p i p_i pi 都相等,即均匀分布。
1.2 拉格朗日乘数法证明 h ( P ) ≤ h ( r c ⊺ ) h(P) ≤ h(\bm{r}\bm{c}^\intercal) h(P)≤h(rc⊺)
虽然比较麻烦,但目前只能用拉格朗日乘子法对付联合概率分布的熵了。先给出函数和限制条件: h ( P ) = − ∑ i , j P i j l o g P i j s u b j u c t t o ∑ j P i j = r i ∑ i P i j = c j \begin{aligned} h(P) &= -\sum_{i,j} {P_{ij}} log{P_{ij}} \\ subjuct \ to \\ \sum_{j} {P_{ij}} &= r_i \\ \sum_{i} {P_{ij}} &= c_j \end{aligned} h(P)subjuct toj∑Piji∑Pij=−i,j∑PijlogPij=ri=cj 由于 r \bm{r} r 和 c \bm{c} c 已限制为概率单纯形,就不必添加 ∑ i , j P i j = 1 \sum_{i,j} {P_{ij}} = 1 ∑i,jPij=1 到限制条件里了。下面进行拉格朗日乘子法求极值:
令 f ( P , α , β ) = − ∑ i , j P i j l o g P i j + ∑ i α i ( ∑ j P i j − r i ) + ∑ j β j ( ∑ i P i j − c j ) \begin{aligned} f(P, \bm{\alpha}, \bm{\beta}) & = -\sum_{i,j} {P_{ij}} log{P_{ij}} \\ & + \sum_{i}\alpha_i(\sum_{j} {P_{ij}} - r_i) \\ & +\sum_{j}\beta_j(\sum_{i} {P_{ij}} - c_j) \end{aligned} f(P,α,β)=−i,j∑PijlogPij+i∑αi(j∑Pij−ri)+j∑βj(i∑Pij−cj) 对 p , α \bm{p}, \bm{\alpha} p,α 和 β \bm{\beta} β 求导,得到 ∂ f ∂ P i j = − ( 1 + l o g P i j ) + α i + β j = 0 ∂ f ∂ α i = ∑ j P i j − r i = 0 ∂ f ∂ β j = ∑ i P i j − c i = 0 \begin{aligned} \frac{\partial f}{\partial P_{ij}} &= -(1 + log{P_{ij}}) + \alpha_i + \beta_j = 0 \\ \frac{\partial f}{\partial \alpha_i} &= \sum_{j} {P_{ij}} - r_i = 0 \\ \frac{\partial f}{\partial \beta_j} &= \sum_{i} {P_{ij}} - c_i = 0 \end{aligned} ∂Pij∂f∂αi∂f∂βj∂f=−(1+logPij)+αi+βj=0=j∑Pij−ri=0=i∑Pij−ci=0 假设对数函数底为 e e e,得 P i j = e α i + β j − 1 P_{ij} = e^{\alpha_i + \beta_j - 1} Pij=eαi+βj−1,这回不是所有的 P i j P_{ij} Pij 都相等了,代入后面两个式子,得 ∑ j P i j = ∑ j e α i + β j − 1 = e α i − 1 ∑ j e β j = r i ⇒ { ∑ j e β j = r i e 1 − α i ① e α i = r i e ∑ j e β j ② ∑ i P i j = ∑ i e α i + β j − 1 = e β j − 1 ∑ i e α i = c j ⇒ ∑ i e α i = c j e 1 − β j ③ \begin{aligned} \sum_{j} {P_{ij}} &= \sum_{j} e^{\alpha_i + \beta_j - 1} \\ &= e^{\alpha_i - 1}\sum_{j} e^{\beta_j } = r_i \\ \Rightarrow & \begin{cases} & \sum_{j} e^{\beta_j } &= r_ie^{1 - \alpha_i} \ ① \\ & e^{\alpha_i} &= \frac{r_ie}{\sum_{j} e^{\beta_j }} \ ② \end{cases}\\ \sum_{i} {P_{ij}} &= \sum_{i} e^{\alpha_i + \beta_j - 1} \\ &= e^{\beta_j - 1}\sum_{i} e^{\alpha_i } = c_j \\ \Rightarrow & \sum_{i} e^{\alpha_i } = c_j e^{1 - \beta_j} \ ③ \\ \end{aligned} j∑Pij⇒i∑Pij⇒=j∑eαi+βj−1=eαi−1j∑eβj=ri{∑jeβjeαi=rie1−αi ①=∑jeβjrie ②=i∑eαi+βj−1=eβj−1i∑eαi=cji∑eαi=cje1−βj ③ 此时,看不出解是什么,仅仅从 ① ① ① 和 ③ ③ ③ 中看出,对于所有的 i i i, r i e 1 − α i r_ie^{1 - \alpha_i} rie1−αi 相等,对于所有的 j j j, c j e 1 − β j c_je^{1 - \beta_j} cje1−βj 相等,看不出什么其他来。那就反向来,我们想要的是 P i j = r i c j P_{ij} = r_ic_j Pij=ricj,正好 ① ① ① 和 ③ ③ ③ 中出现了独立的 r i r_i ri 和 c j c_j cj,相乘得 ① ∗ ③ = ∑ i e α i ∗ ∑ j e β j = r j c j e 2 − α i − β j = r j c j e P i j − 1 \begin{aligned} ① * ③ = \sum_{i} e^{\alpha_i } * \sum_{j} e^{\beta_j} &= r_jc_je^{2-\alpha_i-\beta_j} \\ &= r_jc_jeP_{ij}^{-1} \end{aligned} ①∗③=i∑eαi∗j∑eβj=rjcje2−αi−βj=rjcjePij−1 再求 ∑ i ∗ e α i ∑ j e β j \sum_{i} *\ e^{\alpha_i }\sum_{j} e^{\beta_j} ∑i∗ eαi∑jeβj,累加 ② ② ② 可得 ∑ i e α i = ∑ i r i e ∑ j e β j = e ∑ j e β j ∑ i r i = e ∑ j e β j ⇒ ∑ i e α i ∗ ∑ j e β j = e \begin{aligned} \sum_{i} e^{\alpha_i } &= \sum_{i}\frac{r_ie}{\sum_{j} e^{\beta_j }} \\ &= \frac{e}{\sum_{j} e^{\beta_j }} \sum_{i}r_i \\ &= \frac{e}{\sum_{j} e^{\beta_j }} \\ \Rightarrow & \sum_{i} e^{\alpha_i } * \sum_{j} e^{\beta_j } = e \end{aligned} i∑eαi⇒=i∑∑jeβjrie=∑jeβjei∑ri=∑jeβjei∑eαi∗j∑eβj=e 所以, r j c j e P i j − 1 = e → P i j = r i c j r_jc_jeP_{ij}^{-1} = e \rightarrow P_{ij} = r_ic_j rjcjePij−1=e→Pij=ricj,即 P = r c ⊺ P = \bm{r}\bm{c}^\intercal P=rc⊺ 是一个极值点,再从熵函数的凹性可知其在此极值点取最大值。证毕。
2. 拉格朗日乘子法原理
至此,不等式的证明已经结束。本该结束本文,但问题来了,你知道拉格朗日乘子法是怎么回事吗?它怎么就能求极值点了?于是查阅博客,在《拉格朗日乘子法》一文中找到了详细的解释,在此摘录其主要思想以及一些关键点。
2.1 先看简单的例子:曲线相切
例子
设有二元函数 f ( x , y ) f(x,y) f(x,y) 及其限制条件 g ( x , y ) = 0 g(x,y) = 0 g(x,y)=0 f ( x , y ) = x 2 + y 2 s . t . g ( x , y ) = x y − 1 = 0 \begin{aligned} f(x,y) &= x^2 + y^2 \\ s.t.\ g(x,y) &= xy − 1 = 0 \end{aligned} f(x,y)s.t. g(x,y)=x2+y2=xy−1=0 将三维的 f ( x , y ) f(x,y) f(x,y) 图像投影到 ( x o y ) (xoy) (xoy) 二维平面上,为下图中红色曲线,也称为 f ( x , y ) f(x,y) f(x,y) 的等高线。 g ( x , y ) = 0 g(x,y) = 0 g(x,y)=0 为图中蓝色曲线。

沿着蓝线往内部的圆走,经过橙色点,此时不是最优解,当走到黑色点时,找到了最优解。此时可认为找到了在蓝线这个限制条件下 f ( x , y ) f(x,y) f(x,y) 的最低点。
相切分析
黑点位置,蓝线与圆是相切的,而橙点位置显然不满足这个性质,这正是拉格朗日乘子法的核心。在切点的位置沿蓝线移动很小的一步,都相当于在红色的等高线上移动,这个时候,可以认为函数值已经趋于稳定了,这类似于梯度为 0,可能是一个极值点。
【注】:为什么说 “类似于梯度为 0”?因为在这里, f ( x , y ) f(x,y) f(x,y) 梯度不一定是 0,尤其图中,梯度显然不为 0。但是,蓝色曲线其实就是函数的可行域,就算按梯度下降法优化,那么当前点也只能沿着蓝色曲线走,我称之为 “可行梯度”,那么与等高线相切的地方,“可行梯度” 为 0。不光是曲线,在可行域为曲面或者更高维的几何体时,更新的梯度也要沿着可行域下降,一旦沿着可行域无法下降时,就是可行域的几何体与等高几何体(线或面或更高维几何体)“相切” 了。如果不 “相切”,可行域的几何体就穿过等高几何体,则必有函数值更低的可行点。(当然,如果一个函数从橙色点所在的圆再往内部走是个平底锅,那穿过去再沿着蓝色线走也不下降了,此时是怎么个切法呢?算了,不陷进去,让下面的 λ = 0 \lambda = 0 λ=0 至少还能说得过去。)
从相切到梯度
相切,意味着在切点的位置,等高线和蓝色曲线的等高线方向是平行的,考虑到梯度与等高线垂直,我们可以用两条曲线的梯度平行来求出切点位置。
【注】:本人认为这里 “两条曲线的梯度” 的说法不合适,曲线哪来的梯度?我明白作者想说什么,大约就是:函数 f ( x , y ) f(x, y) f(x,y) 的梯度方向是垂直于等高线的。那 g ( x , y ) = 0 g(x, y) = 0 g(x,y)=0 这个方程怎么叫梯度呢?我隐约记得大一的高等数学里有求曲线方向的,还有曲面的法向量。从知乎博文《曲面的切平面的推导过程的逻辑》 温习了其中的原理。可知, ▽ g \bigtriangledown g ▽g 是曲线的垂直线。那么就可以说 “使 f ( x , y ) f(x, y) f(x,y) 的梯度方向与 g ( x , y ) = 0 g(x, y) = 0 g(x,y)=0 曲线的垂直方向平行来求出切点位置”。
所以有: ▽ f = λ ▽ g \bigtriangledown f = \lambda \bigtriangledown g ▽f=λ▽g,其中 λ \lambda λ 表示一个标量,保证它们的方向相同即可。对于上面的例子,我们可以求出函数 f f f 和 g g g 的偏导,组成方程组 ( 1 ) (1) (1) ∂ f ∂ x = λ ∂ g ∂ x ∂ f ∂ y = λ ∂ g ∂ y g ( x , y ) = 0 \begin{aligned} \frac{\partial f}{\partial x} &= \lambda \frac{\partial g}{\partial x} \\ \frac{\partial f}{\partial y} &= \lambda \frac{\partial g}{\partial y} \\ g(x, y) &= 0 \end{aligned} ∂x∂f∂y∂fg(x,y)=λ∂x∂g=λ∂y∂g=0 使用一个统一的拉格朗日函数: L ( x , y , λ ) = f ( x , y ) − λ g ( x , y ) L(x, y, \lambda) = f(x, y) - \lambda g(x, y) L(x,y,λ)=f(x,y)−λg(x,y),令这个函数偏导为 0,可以得到方程组 ( 2 ) (2) (2):
∂ L ∂ x = ∂ f ∂ x − λ ∂ g ∂ x = 0 ∂ L ∂ y = ∂ f ∂ y − λ ∂ g ∂ y = 0 ∂ L ∂ λ = − g ( x , y ) = 0 \begin{aligned} \frac{\partial L}{\partial x} &= \frac{\partial f}{\partial x} - \lambda \frac{\partial g}{\partial x} = 0 \\ \frac{\partial L}{\partial y} &= \frac{\partial f}{\partial y} - \lambda \frac{\partial g}{\partial y} = 0 \\ \frac{\partial L}{\partial \lambda} &= -g(x, y) = 0 \end{aligned} ∂x∂L∂y∂L∂λ∂L=∂x∂f−λ∂x∂g=0=∂y∂f−λ∂y∂g=0=−g(x,y)=0 可以发现方程组 ( 2 ) (2) (2) 与方程组 ( 1 ) (1) (1) 一样,联立以上三式即可求出 x , y , λ x, y, \lambda x,y,λ 的值。 λ \lambda λ 前是 + + + 是 − - − 一样的。
2.2 更多限制条件
如果是多个约束条件,该如何解释呢?首先,多个约束条件联立依然是决定了可行域。拉格朗日函数为: L ( x 1 , … , x n , λ 1 , … , λ k ) = f ( x 1 , … , x n ) − ∑ j = 1 k λ j g j ( x 1 , … , x n ) L(x_1, …, x_n, \lambda_1, …, \lambda_k) = f(x_1, …, x_n) - \sum_{j=1}^k \lambda_jg_j(x_1, …, x_n) L(x1,…,xn,λ1,…,λk)=f(x1,…,xn)−j=1∑kλjgj(x1,…,xn) 为什么直接累加多个 λ j ∗ g j \lambda_j * g_j λj∗gj 就可以了?这可以从两个角度去解释。
解析几何角度
举个最简单的例子,如果 f ( x , y , z ) f(x, y, z) f(x,y,z) 是三元函数,有一个限制条件 g 1 ( x , y , z ) = 0 g_1(x, y, z) = 0 g1(x,y,z)=0(一个曲面),根据上面的 “相切” 分析,我们知道在切点, f ( x , y , z ) f(x, y, z) f(x,y,z) 的梯度与 g 1 ( x , y , z ) = 0 g_1(x, y, z) = 0 g1(x,y,z)=0 的法向量平行,即 ▽ f = λ 1 ▽ g 1 \bigtriangledown f = \lambda_1 \bigtriangledown g_1 ▽f=λ1▽g1。如果再加一个限制条件 g 2 ( x , y , z ) = 0 g_2(x, y, z) = 0 g2(x,y,z)=0,那可行域就变成了一条三维空间中的曲线(大概率),按照上面的说法 “可以用两条曲线的梯度平行来求出切点位置”,等高线(面)的梯度方向与曲线的梯度方向平行,但这是三维空间,曲线的梯度方向在哪?不好说。
就换个角度说吧,回顾 “在切点的位置沿蓝线移动很小的一步,都相当于在红色的等高线上移动”,其实这是说移动方向在函数梯度方向的分量为 0,也即垂直于函数梯度方向。正好,两个曲面的法向量的任意组合 ( λ 1 ▽ g 1 + λ 2 ▽ g 2 ) (\lambda_1 \bigtriangledown g_1 + \lambda_2 \bigtriangledown g_2) (λ1▽g1+λ2▽g2) 表示一个“平面”,其法向量就是可行曲线,只要保证函数梯度平行于面 ( λ 1 ▽ g 1 + λ 2 ▽ g 2 ) (\lambda_1 \bigtriangledown g_1 + \lambda_2 \bigtriangledown g_2) (λ1▽g1+λ2▽g2) 就能保证 “移动方向在函数梯度方向的分量为 0”。所以 ▽ f = λ 1 ▽ g 1 + λ 2 ▽ g 2 ) \bigtriangledown f = \lambda_1 \bigtriangledown g_1 + \lambda_2 \bigtriangledown g_2) ▽f=λ1▽g1+λ2▽g2)。下图的黄色曲线,只要不穿过去,随意动,都满足该等式。
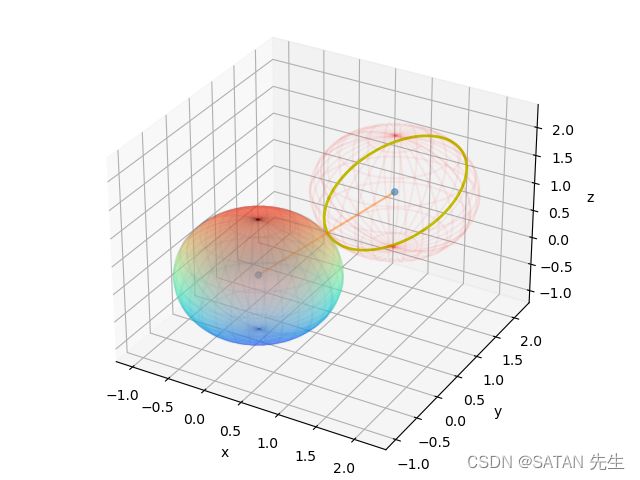
那么更多限制条件呢?其实,无论多少限制条件, ∑ i λ i ▽ g i \sum_i \lambda_i \bigtriangledown g_i ∑iλi▽gi 都与可行域正交, ▽ f = ∑ i λ i ▽ g i \bigtriangledown f = \sum_i \lambda_i \bigtriangledown g_i ▽f=∑iλi▽gi 与可行域正交保证在相切点附近的可行域移动不会在函数梯度上有分量。
归纳角度
一个限制条件很好解释,不多说了。当来一个新条件时,我们把 L ( x 1 , … , x n , λ 1 ) = f ( x 1 , … , x n ) + λ 1 g 1 ( x 1 , … , x n ) L(x_1, …, x_n, \lambda_1) = f(x_1, …, x_n) + \lambda_1g_1(x_1, …, x_n) L(x1,…,xn,λ1)=f(x1,…,xn)+λ1g1(x1,…,xn) 看作一个函数,求它的极值,新条件 g 2 ( x 1 , … , x n ) g_2(x_1, …, x_n) g2(x1,…,xn) 是 L ( x 1 , … , x n , λ 1 ) L(x_1, …, x_n, \lambda_1) L(x1,…,xn,λ1) 的限制条件,那么就有 L ( x 1 , … , x n , λ 1 , λ 2 ) = f ( x 1 , … , x n ) + λ 1 g 1 ( x 1 , … , x n ) + λ 2 g 2 ( x 1 , … , x n ) L(x_1, …, x_n, \lambda_1, \lambda_2) = f(x_1, …, x_n) + \lambda_1g_1(x_1, …, x_n) + \lambda_2g_2(x_1, …, x_n) L(x1,…,xn,λ1,λ2)=f(x1,…,xn)+λ1g1(x1,…,xn)+λ2g2(x1,…,xn),依次类推。这么解释简单明了。只不过没有解析几何角度更有直觉感。
以上是等式约束下的拉格朗日乘子法,关于不等式约束下的情况,博文《优化-拉格朗日乘子法》讲的比较直观易懂。
2.3 拉格朗日乘子法与正态分布的由来
另外,已知均值和方差的情况下,用拉格朗日乘数法求最大熵,可以求得正态分布是熵最大的分布,解释了现实中正态分布如此常见的原因。详情可见博文《最大熵与正态分布》和《正太分布的前世今生》。限于数学基础,没看太懂。
3. 信息论基础
其实,要是熟悉信息论的基础概念,上面的这些证明都不必,公式 ( 1 ) (1) (1) 很简单。有必要较为系统地整理一下信息熵的基础知识了。
| 概念 | 公式 | 直觉意义 |
|---|---|---|
| 熵:entropy | H ( X ) = − ∑ x p ( x ) l o g p ( x ) H(X) = −\sum_x p(x)logp(x) H(X)=−∑xp(x)logp(x) | 平均信息量,不确定性的度量 |
| 相对熵:relative entropy | D ( p ∣ ∣ q ) = ∑ x p ( x ) l o g p ( x ) q ( x ) D(p||q) = \sum_x p(x)log\frac{p(x)}{q(x)} D(p∣∣q)=∑xp(x)logq(x)p(x) | KL 散度,衡量低效程度:真实分布为 p p p,却假设为 q q q。编码变长了多少? |
| 互信息:mutual information | I ( X , Y ) = ∑ x , y p ( x , y ) l o g p ( x , y ) p ( x ) p ( y ) I(X,Y) = \sum_{x,y} p(x,y)log\frac{p(x,y)}{p(x)p(y)} I(X,Y)=∑x,yp(x,y)logp(x)p(y)p(x,y) | the reduction in the uncertainty of X due to the knowledge of Y |
3.1 熵和信息编码

这个例子想表示:用前缀码表示胜利马的平均码长最短等于熵。这个是哈夫曼编码(最优前缀码)
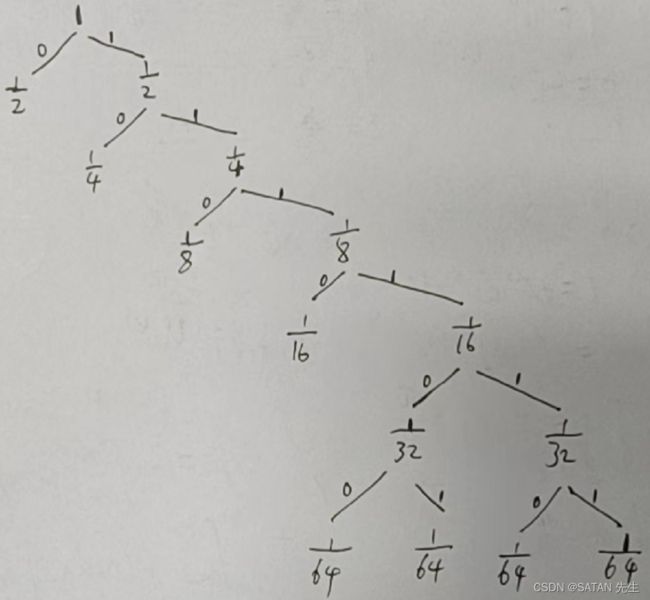
每个编码的长度就是结点所处的哈夫曼树的深度,所以底为 2。
3.2 联合分布熵和条件熵
H ( X , Y ) = − ∑ x , y p ( x , y ) l o g p ( x , y ) H(X,Y) = −\sum_{x,y} p(x,y)logp(x,y) H(X,Y)=−x,y∑p(x,y)logp(x,y) 依然是求平均信息量。条件熵

限定每一个 x,然后取平均。限定 X 后,Y 所剩不确定度。

整个的不确定度由 X 的不确定度和“限定 X 后 Y 的不确定度”相加。
3.3 相对熵(KL 散度) 非负
可用于证明不等式 ( 1 ) (1) (1)。下面用 Jensen 不等式 E f ( X ) ≥ f ( E X ) Ef(X) \geq f(EX) Ef(X)≥f(EX), f f f 为凸函数,若凹则反,证明 D ( p ∥ q ) ≥ 0 D(p\|q) \geq 0 D(p∥q)≥0:

l o g log log 是凹,故 ≤ \leq ≤。这里的 l o g q ( x ) p ( x ) log\frac{q(x)}{p(x)} logp(x)q(x) 看起来像是函数,其实用 Jensen 不等式的时候, q ( x ) p ( x ) \frac{q(x)}{p(x)} p(x)q(x) 被看作了 X X X 取值。
3.4 互信息
定义为 joint distribution p ( x , y ) p(x, y) p(x,y) 和 product distribution p ( x ) p ( y ) p(x)p(y) p(x)p(y) 之间的 relative entropy I ( X , Y ) = ∑ x , y p ( x , y ) l o g p ( x , y ) p ( x ) p ( y ) = ∑ x , y p ( x , y ) l o g p ( x , y ) − ∑ x , y p ( x , y ) l o g ( p ( x ) p ( y ) ) = − H ( X , Y ) − ∑ x , y p ( x , y ) l o g p ( x ) − ∑ x , y p ( x , y ) l o g p ( y ) = − H ( X , Y ) − ∑ x p ( x ) l o g p ( x ) − ∑ y p ( y ) l o g p ( y ) = − H ( X , Y ) + H ( X ) + H ( Y ) \begin{aligned} I(X,Y) &= \sum_{x,y} p(x,y)log\frac{p(x,y)}{p(x)p(y)} \\ &= \sum_{x,y} p(x,y)logp(x,y) − \sum_{x,y} p(x,y)log(p(x)p(y)) \\ &= -H(X,Y) − \sum_{x,y} p(x,y)logp(x) − \sum_{x,y} p(x,y)logp(y) \\ &= -H(X,Y) − \sum_{x} p(x)logp(x) − \sum_{y} p(y)logp(y) \\ &= -H(X,Y) + H(X) + H(Y) \end{aligned} I(X,Y)=x,y∑p(x,y)logp(x)p(y)p(x,y)=x,y∑p(x,y)logp(x,y)−x,y∑p(x,y)log(p(x)p(y))=−H(X,Y)−x,y∑p(x,y)logp(x)−x,y∑p(x,y)logp(y)=−H(X,Y)−x∑p(x)logp(x)−y∑p(y)logp(y)=−H(X,Y)+H(X)+H(Y) 解释为 the reduction in the uncertainty of X due to the knowledge of Y,由于相对熵非负,互信息本身就是一个相对熵,所以互信息非负 I ( X , Y ) ≥ 0 I(X,Y) \geq 0 I(X,Y)≥0,这样就可以轻松证明不等式 ( 1 ) (1) (1) 了 I ( X , Y ) = − H ( X , Y ) + H ( X ) + H ( Y ) ≥ 0 ⇒ H ( X , Y ) ≤ H ( X ) + H ( Y ) \begin{aligned} I(X,&Y) = -H(X,Y) + H(X) + H(Y) \geq 0 \\ &\Rightarrow H(X, Y) \leq H(X) + H(Y) \end{aligned} I(X,Y)=−H(X,Y)+H(X)+H(Y)≥0⇒H(X,Y)≤H(X)+H(Y)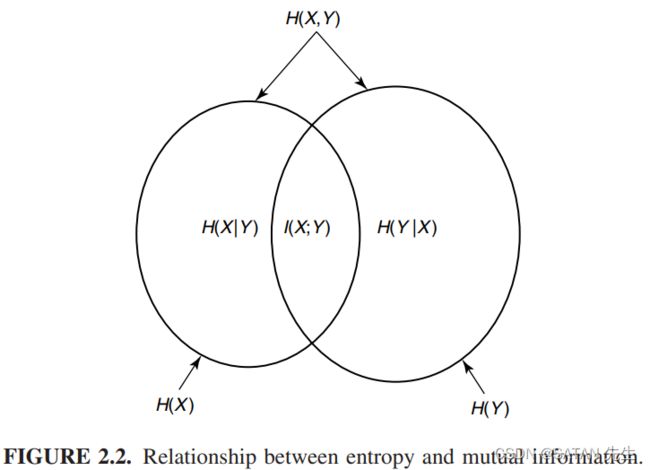
不确定性也可以这么直观。 H ( X ∣ Y ) H(X|Y) H(X∣Y) 是 Y Y Y 干预后, X X X 分布所剩不确定度,干预是指:在 Y Y Y 取不同值时, X X X 的分布受到影响而可能不同,又由于 H ( X ) H(X) H(X) 是凹函数(其每个分量都是凹的),则: H ( X ∣ Y ) = ∑ y p ( y ) H ( X ∣ Y = y ) ≤ H ( ∑ y p ( y ) ( X ∣ Y = y ) ) = H ( ∑ y ( X , Y = y ) ) / ∗ 联 合 分 布 矩 阵 行 和 ∗ / = H ( X ) ⇒ H ( X ∣ Y ) ≤ H ( X ) \begin{aligned} H(X|Y) &= \sum_yp(y)H(X|Y=y) \\ &\leq H(\sum_y p(y)(X|Y=y)) \\ &= H(\sum_y(X, Y=y)) \ /*联合分布矩阵行和*/ \\ &= H(X) \\ \Rightarrow H(X|Y) & \leq H(X) \end{aligned} H(X∣Y)⇒H(X∣Y)=y∑p(y)H(X∣Y=y)≤H(y∑p(y)(X∣Y=y))=H(y∑(X,Y=y)) /∗联合分布矩阵行和∗/=H(X)≤H(X) 当不同 ( Y = y ) (Y=y) (Y=y) 下, ( X ∣ Y = y ) (X|Y=y) (X∣Y=y) 都相同时,等号成立。 Y Y Y 的出现减少了 X X X 的不确定度。以上是从公式的角度说明熵是减少的,还是不够直观啊。
还是举个栗子吧:赛马,8 匹马 10 个场地,各马获胜的概率分布为 p ( X ) p(X) p(X),场地选择随机分布 p ( Y ) p(Y) p(Y),选择不同比赛场地 8 匹马获胜概率分布 p ( X ∣ Y = y j ) p(X|Y=y_j) p(X∣Y=yj) 不同;现在,有 10 场比赛,但不知道在哪,你要下注,你肯定每次都选择概率最大的那匹马,但当你知道各场比赛的场地时,你就更加确定这些场次都该选哪匹马。至于 ∑ y p ( y ) H ( X ∣ Y = y ) \sum_yp(y)H(X|Y=y) ∑yp(y)H(X∣Y=y),就是取个加权平均。
所以,可以定义互信息为 the reduction in the uncertainty of X due to the knowledge of Y I ( X ∣ Y ) = H ( X ) − H ( X ∣ Y ) = − ∑ x p ( x ) l o g p ( x ) − ∑ y p ( y ) H ( X ∣ Y = y ) = − ∑ x p ( x ) l o g p ( x ) + ∑ y p ( y ) ∑ x p ( x ∣ y ) l o g p ( x ∣ y ) = − ∑ y ∑ x p ( x , y ) l o g p ( x ) + ∑ y ∑ x p ( x , y ) l o g p ( x ∣ y ) = ∑ x ∑ y p ( x , y ) [ l o g p ( x ∣ y ) − l o g p ( x ) ] = ∑ x ∑ y p ( x , y ) l o g p ( x ∣ y ) = p ( x , y ) p ( y ) l o g p ( x ) = ∑ x ∑ y p ( x , y ) l o g p ( x , y ) l o g [ p ( x ) p ( y ) ] \begin{aligned} I(X|Y) &= H(X) - H(X|Y) \\ &= -\sum_xp(x)logp(x) - \sum_yp(y)H(X|Y=y) \\ &= -\sum_xp(x)logp(x) + \sum_yp(y)\sum_xp(x|y)logp(x|y) \\ &= -\sum_y\sum_xp(x,y)logp(x) + \sum_y\sum_xp(x,y)logp(x|y) \\ &= \sum_x\sum_yp(x,y)[logp(x|y) - logp(x)] \\ &= \sum_x\sum_yp(x,y)log\frac{p(x|y)=\frac{p(x,y)}{p(y)}}{logp(x)} \\ &= \sum_x\sum_yp(x,y)log\frac{p(x,y)}{log[p(x)p(y)]} \end{aligned} I(X∣Y)=H(X)−H(X∣Y)=−x∑p(x)logp(x)−y∑p(y)H(X∣Y=y)=−x∑p(x)logp(x)+y∑p(y)x∑p(x∣y)logp(x∣y)=−y∑x∑p(x,y)logp(x)+y∑x∑p(x,y)logp(x∣y)=x∑y∑p(x,y)[logp(x∣y)−logp(x)]=x∑y∑p(x,y)loglogp(x)p(x∣y)=p(y)p(x,y)=x∑y∑p(x,y)loglog[p(x)p(y)]p(x,y) X X X 和 Y Y Y 相互对称。
4. 交叉熵、sigmoid 和 正负均衡问题
既然讲到了熵,那就趁热把之前关于交叉熵的稀里糊涂的问题搞清楚。关于为什么分类用交叉熵已经很清楚(梯度问题),不说了。这里主要谈一谈正负均衡问题,这个问题来源于我之前写的一段关于 Logistics Regression 的损失函数代码:
imgs, lbs = data
y = np.matmul(imgs, self.__W) + self.__b
# 这个损失函数并不是什么交叉熵,而是单个考虑的 -ln(sigmoid)
# 有点像二分类交叉熵,只不过在各个输出节点分开左右的对称中心是 x=0,不是 x=1/2
# + 的时候是 softplus(-x), - 的时候是 softplus(x)
# 总的来说,就是对正负样本都进行优化,正的向右,负的向左
pos = self.__num_cls - 1
neg = self.__num_cls - 2
loss = np.mean(-pos * lbs * y + (neg * lbs + 1) * softplus(y), axis=-1)
loss = np.sum(loss)
写这段代码时还很年轻。代码用于 MNIST 分类,按理来说应该直接用交叉熵的,也许是因为年轻,也许是故意学习 Logistics Regression,就用了 s i g m o i d sigmoid sigmoid,确切来说是 − l o g ( s i g m o i d ( x ) ) = s o f t p l u s ( − x ) -log(sigmoid(x)) = softplus(-x) −log(sigmoid(x))=softplus(−x),图像如下

正样本沿着蓝线 s o f t p l u s ( − x ) softplus(-x) softplus(−x) 往右推,负样本沿着红线 s o f t p l u s ( x ) softplus(x) softplus(x) 往左推。
4.1 正负样本均衡问题
MNIST 有 10 个类别,一张图片上有一个数字,如果强行用 s i g m o i d sigmoid sigmoid 而不是 s o f t m a x softmax softmax,则需要输出 10 个结点,每个结点关联一个数字,按 s i g m o i d sigmoid sigmoid 二分类(是否是当前数字),相当于进行了 10 个平行的逻辑结点。问题来了,当输入一张图片时,10 个结点只有一个是正,其余是负,长此以往,假如 10 个类别均衡,则每个结点为正的机会是为负机会的 1 / 9 1/9 1/9,即正负不均衡,这会不会由于负能量太大导致 W x + b Wx+b Wx+b 被推向负的,使正样本也搞不到正能量?不太清楚。但上述代码实现了正负均衡,就不用担心这个问题了:正样本乘 9。
刚才说这不是交叉熵,真正的二分类交叉熵是 l o s s = − l b l ∗ l o g y − ( 1 − l b l ) ∗ l o g ( 1 − y ) y = p ( x ) = s i g m o i d ( x ) = 1 1 + e − x \begin{aligned} loss &= -lbl * logy - (1-lbl) * log(1-y) \\ y &= p(x) = sigmoid(x) =\frac{1}{1+e^{-x}} \end{aligned} lossy=−lbl∗logy−(1−lbl)∗log(1−y)=p(x)=sigmoid(x)=1+e−x1 当 l b l = 1 lbl = 1 lbl=1 时 l o s s = − l o g ( 1 1 + e − x ) = l o g ( 1 + e − x ) loss = -log(\frac{1}{1+e^{-x}}) = log(1+e^{-x}) loss=−log(1+e−x1)=log(1+e−x) 哎!就是图中的蓝色曲线;当 l b l = 0 lbl = 0 lbl=0 时, l o s s = − l o g ( 1 − 1 1 + e − x ) = − l o g ( 1 + e − x − 1 1 + e − x ) = l o g ( 1 + e − x e − x ) = l o g ( 1 + e x ) loss = -log(1 - \frac{1}{1+e^{-x}}) = -log(\frac{1+e^{-x}-1}{1+e^{-x}}) = log(\frac{1+e^{-x}}{e^{-x}}) = log(1+e^{x}) loss=−log(1−1+e−x1)=−log(1+e−x1+e−x−1)=log(e−x1+e−x)=log(1+ex) 哎!就是图中的红色曲线;一模一样。看来年轻的时候还是太草率啊,把正负 l o s s loss loss “关于 y = s i g m o i d ( x ) = 1 / 2 y = sigmoid(x) = 1/2 y=sigmoid(x)=1/2 对称” 当成了 “关于 x = 1 / 2 x = 1/2 x=1/2 对称”,以至于认为所使用的 s o f t p l u s softplus softplus 不是交叉熵。
loss = np.mean(-pos * lbs * y + (neg * lbs + 1) * softplus(y), axis=-1)来源于 l o g ( 1 + e − x ) = l o g [ e − x ( 1 + e x ) ] = − x + l o g ( 1 + e x ) log(1+e^{-x}) = log[e^{-x}(1+e^{x})] = -x + log(1+e^{x}) log(1+e−x)=log[e−x(1+ex)]=−x+log(1+ex),好麻烦,实际该这么写
loss = np.mean( pos * lbs * softplus(-y) + (1 - lbs) * softplus(y), axis=-1 )这比较清晰,要说当初为啥写得那么隐匿?估计就是为了少算一次 s o f t p l u s softplus softplus 吧。
4.2 多标签多分类中的正负均衡
至此,对于单标签的多分类问题在使用 s i g m o i d sigmoid sigmoid 时的正负不均衡问题已经搞清楚,也已解决。如果多标签呢?在博文《一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉》中提到多标签的多分类问题,图片中可能有多种小动物,建立模型判断一张图片中有哪些小动物

与上面的 MNIST 是做法是一样的,计算出 n(总类别数)个输出结点,对每个结点实施 “有或无” 的 s i g m o i d sigmoid sigmoid 二分类,只不过作者没说正负均衡的事。
假如平均每张图片含 m 种小动物,那么:每个结点正负能量比为 m : ( n − m ) m : (n-m) m:(n−m),当 n > > m n >> m n>>m 时,正负能量就会严重失衡。所以,让正能量变大,使得 α m : ( n − m ) = 1 : 1 \alpha m : (n-m) = 1:1 αm:(n−m)=1:1,则 α = n m − 1 \alpha = \frac{n}{m} - 1 α=mn−1,这个值就是上面 MNIST 中的 9,应该能实现正负能量均衡吧。代码和上面一样的(多分类的标签是 n − h o t n-hot n−hot)。
4.3 交叉熵相当均衡
哎!多分类的交叉熵是不是均衡的?可别忘了 l o s s = − ∑ p ( x ) l o g q ( x ) loss = -\sum p(x)logq(x) loss=−∑p(x)logq(x) 仅仅有一个 p ( x i ) p(x_i) p(xi) 为 1,每个输出结点正负的比值依然是 1 / 9 1/9 1/9(上面的MNIST)。先说结论:是均衡的。
这里情况不同了,因为结点正负时的优化函数不一样了,而上面的基于 s i g m o i d sigmoid sigmoid 的多分类正负优化函数仅关于 x = 0 x=0 x=0 对称,也就是说不管结点是正是负,梯度待遇是一样的。多分类的交叉熵函数使正结点梯度大,负结点梯度小。以 MNIST 为例,假设当前标签为 l a b e l = ( 0 , 0 , 1 , 0... , 0 ) label = (0, 0, 1, 0..., 0) label=(0,0,1,0...,0),网络输出结点为 ( x 0 , x 1 , . . . , x 9 ) (x_0, x_1, ..., x_9) (x0,x1,...,x9),看导数: l o s s = − ∑ i = 0 9 ( l a b e l i ∗ l o g e x i ∑ j = 0 9 e x j ) = − l o g e x 2 ∑ j = 0 9 e x j ∂ l o s s ∂ x 2 = − ∑ j = 0 9 e x j e x 2 ∗ e x 2 ∗ ( ∑ j = 0 9 e x j ) − e x 2 ∗ e x 2 ( ∑ j = 0 9 e x j ) 2 = − ∑ j = 0 9 e x j e x 2 ∗ e x 2 ∑ j = 0 9 e x j ∗ ( 1 − e x 2 ∑ j = 0 9 e x j ) = e x 2 ∑ j = 0 9 e x j − 1 = − ∑ k ≠ 2 e x k ∑ j = 0 9 e x j ∂ l o s s ∂ x 3 = − ∑ j = 0 9 e x j e x 2 ∗ − e x 2 ∗ e x 3 ( ∑ j = 0 9 e x j ) 2 = e x 3 ∑ j = 0 9 e x j \begin{aligned} loss &= -\sum_{i=0}^9 (label_i * log \frac{e^{x_i}}{\sum_{j=0}^9 e^{x_j}}) \\ &= -log \frac{e^{x_2}}{\sum_{j=0}^9 e^{x_j}} \\ \frac{\partial loss}{\partial x_2} &= -\frac{\sum_{j=0}^9 e^{x_j}}{e^{x_2}} * \frac{e^{x_2} * (\sum_{j=0}^9 e^{x_j}) - e^{x_2} * e^{x_2}}{(\sum_{j=0}^9 e^{x_j})^2} \\ &= -\frac{\sum_{j=0}^9 e^{x_j}}{e^{x_2}} * \frac{e^{x_2}}{\sum_{j=0}^9 e^{x_j}} *(1-\frac{e^{x_2}}{\sum_{j=0}^9 e^{x_j}}) \\ &= \frac{e^{x_2}}{\sum_{j=0}^9 e^{x_j}} - 1 \\ &= -\sum_{k \neq 2}\frac{e^{x_k}}{\sum_{j=0}^9 e^{x_j}} \\ \frac{\partial loss}{\partial x_3} &= -\frac{\sum_{j=0}^9 e^{x_j}}{e^{x_2}} * \frac{- e^{x_2} * e^{x_3}}{(\sum_{j=0}^9 e^{x_j})^2} \\ &= \frac{e^{x_3}}{\sum_{j=0}^9 e^{x_j}} \\ \end{aligned} loss∂x2∂loss∂x3∂loss=−i=0∑9(labeli∗log∑j=09exjexi)=−log∑j=09exjex2=−ex2∑j=09exj∗(∑j=09exj)2ex2∗(∑j=09exj)−ex2∗ex2=−ex2∑j=09exj∗∑j=09exjex2∗(1−∑j=09exjex2)=∑j=09exjex2−1=−k=2∑∑j=09exjexk=−ex2∑j=09exj∗(∑j=09exj)2−ex2∗ex3=∑j=09exjex3 注意到 ∂ l o s s ∂ x 2 = − ∑ k ≠ 2 ∂ l o s s ∂ x k \begin{aligned} \frac{\partial loss}{\partial x_2} = -\sum_{k \neq 2} \frac{\partial loss}{\partial x_k} \end{aligned} ∂x2∂loss=−k=2∑∂xk∂loss 这么一看,交叉熵损失函数使正负样本在梯度上绝对平衡。这也许是交叉熵损失的一大优势吧。
再想一想,好像均方误差 MSE 的正负是不均衡的哦!