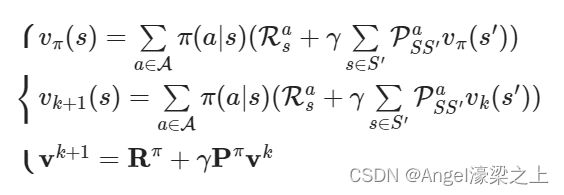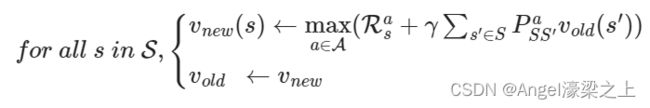David Silver强化学习公开课自学笔记——Lec3动态规划

本笔记摘自知乎博主旺财的搬砖历险记和叶强，仅用于自学

1.动态规划介绍

（1）定义

Dynamic： sequential or temporal component to the problem.
Programming：optimising a “problem”

动态：该问题的时间或序列部分
规划：优化一个策略，与线性规划不同

动态规划

• 是解决复杂问题的一个方法
• 把复杂问题分解问子问题
  • 求解子问题
  • 通过整合子问题的解得到整个问题的解
• 子问题的结果通常被存储从而解决后续复杂问题

（2）求解问题范围

不是所有的问题都能用动态规划方法来求解，能用动态规划求解的问题必须满足两个性质：

• 最优子结构（Optimal substructure）
  • 保证问题能够使用最优性原理
  • 问题的最优解可以分解为子问题的最优解
• 重叠子问题（Overlapping subproblems）
  • 子问题重复多次
  • 可以缓存并重用子问题的解

多阶段决策过程的最优决策序列具有这样的性质：
不管初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略

MDP满足最优子结构和重叠子问题：

• 贝尔曼方程是递归的形式，把问题递归为求解子问题
• 值函数相当于存储了子问题的解，可以重用

（3）MDP

规划：

• 用动态规划算法，在了解整个MDP的基础上，求解最优策略。即，在清楚模型结构（状态行为空间、转换矩阵、奖励等）的基础上，用规划来进行预测和控制。

1)预测

⭐输入：给定一个MDP$⟨\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma ⟩$和策略$\pi$，或者给定一个MRP$⟨\mathcal{S},{\mathcal{P}}^{\pi },{\mathcal{R}}^{\pi },\gamma ⟩$
⭐输出：基于当前策略的值函数$v_{\pi }$

2)控制

⭐输入：给定一个MDP$⟨\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma ⟩$
⭐输出：最优价值函数$v_{\ast }$和最优策略${\pi }_{\ast }$

（5）DP解决其他问题

（Richard Bellman在1957年出版作品《Dynamic Programming》）

• 调度算法 Scheduling algorithms
• 字符串算法 String algorithms （eg. sequence alignment）
• 图算法 Graph algorithms（eg. shortest path algorithms）
• 图形模型 Graphical models（eg. Viterbi algorithm）
• 生物信息学 Bioinformatics（eg. lattice models）

2.策略评估

（1）迭代策略评估

❓问题：评估一个给定的策略，也就是解决“预测”问题

• 给定一个策略$\pi$，求对应的值函数$v_{\pi }(s)$或$q_{\pi }(s,a)$

✏解决：

• 直接解：$v_{\pi }=(1-\gamma {\mathcal{P}}^{\pi }{)}^{-1}{\mathcal{R}}^{\pi }$，可以求得精确解，但是复杂度$\mathcal{O}(n^3)$
• 迭代解：应用Bellman期望方程，反向迭代✅$v_{\pi }(s)=\mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]$，$v_1\to v_2\to \dots v_{\pi }$

方法：

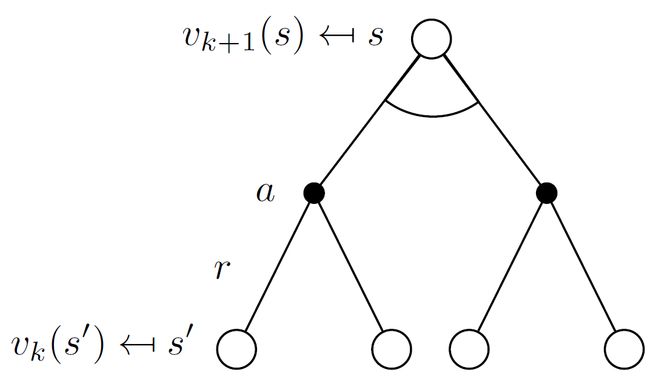
• 同步反向迭代（synchronous backups）

  • 在每次迭代过程中，对于第$k+1$次迭代，所有的状态$s\in \mathcal{S}$的价值用$v_k(s^{\prime })$计算，并以$v_k(s^{\prime })$更新该状态在第$k+1$次迭代中的价值$v_{k+1}(s)$（$s^{\prime }$是$s$的后继状态）
  • 解释
    • synchronous：同步，指每次更新都要更新完所有的状态
    • backup：备份，即$v_{k+1}(s)$需要用到$v_k(s^{\prime })$，以$v_k(s^{\prime })$更新$v_{k+1}(s)$的过程称为备份，更新状态$s$的值函数称为备份状态$s$
  • 公式
    • 一次迭代内，状态$s$的价值等于前次迭代里该状态的即时奖励➕所有可能的下一个状态$s^{\prime }$的价值与其概率的乘积
      

• 异步反向迭代（asynchronous backups）

  • 在第$k$次迭代时使用当此迭代的状态价值来更新状态价值

（2）举例：方格世界

• 已知条件
  • 状态空间$S$：$S1-S14$为非终止状态，$ST$为终止状态。
  • 动作空间$A$：东南西北四个方向。
  • 转移概率$P$：动不了就停在原地，其余按照动作方向运动。
  • 即时奖励$R$：进入非终止状态的即时奖励为-1，进入终止状态即时奖励为0。
  • 衰减系数$\gamma$：1。
  • 当前策略$\pi$：随机策略，各动作的概率均为25%
• 问题
  • 评估在这个方格世界里给定的策略。即，求解该方格世界在给定策略下的状态价值函数，求每一个状态的价值。
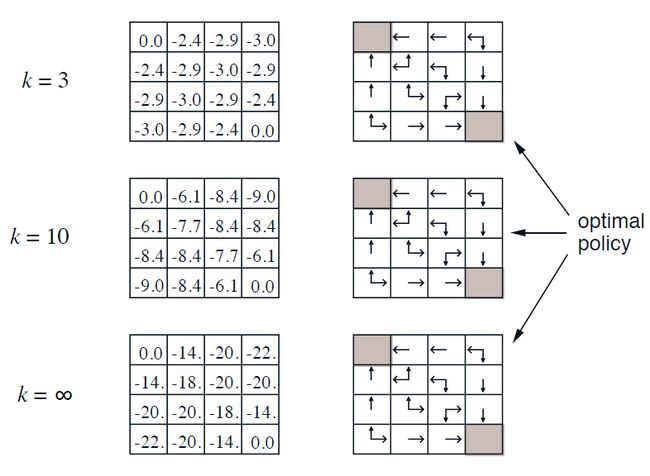
• 迭代法求解
• 

迭代次数	注释
k=0	根据当前的状态价值，无法得出比随机策略更好的策略
k=1	向上到边界，位置不变，且v(s’)仍用k=0时的价值 $v_{\pi }(s)={\sum }_{a\in \mathcal{A}}\pi (a|s)({\mathcal{R}}_s^a+\gamma {\sum }_{s\in S^{\prime }}{\mathcal{P}}_{S{S}^{\prime }}^a{v}_{\pi }(s^{\prime }))$ （1，2）处的$-1=\uparrow 0.25(-1+1\ast (1\ast 0))+\to 0.25(-1+1\ast (1\ast 0))+\downarrow 0.25(-1+1\ast (1\ast 0))+\leftarrow 0.25(-1+1\ast (1\ast 0))$
k=2	目前未得到最优策略 （1，2）处的$-1.7=\uparrow 0.25(-1+1\ast (1\ast -1))+\to 0.25(-1+1\ast (1\ast -1))+\downarrow 0.25(-1+1\ast (1\ast -1))+\leftarrow 0.25(-1+1\ast (1\ast 0))$ （3，2）处的$-2=\uparrow 0.25(-1+1\ast (1\ast -1))+\to 0.25(-1+1\ast (1\ast -1))+\downarrow 0.25(-1+1\ast (1\ast -1))+\leftarrow 0.25(-1+1\ast (1\ast 1))$
k=3	根据该状态价值函数已经可以得到最优策略 （2，4）处的$-2.9=\uparrow 0.25(-1+1\ast (1\ast -2))+\to 0.25(-1+1\ast (1\ast -2))+\downarrow 0.25(-1+1\ast (1\ast -1.7))+\leftarrow 0.25(-1+1\ast (1\ast -2))$

使用python计算后，状态价值在第153次迭代后收敛。
注意：

• 这里${\mathcal{P}}_{S{S}^{\prime }}^a$全为1
• 这里只是使用贝尔曼期望方程进行策略估计，没有对策略进行改进

3.策略迭代

如果要解决控制问题，不光是预测问题，必须进行策略改进，希望找到某个问题的最优策略。

（1）如何改善策略

给定一个策略

• 评估该策略：$$v\pi (s)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+\dots |S_t=s]$$
• 在当前策略上，贪婪选择策略，使得后续状态价值最多：$${\pi }^{\prime }=greedy(v_{\pi })$$
  在方格世界中
• 基于给定策略的价值迭代最终收敛得到的策略就是最优策略：$${\pi }^{\prime }={\pi }^{\ast }$$
• 通常，需要更多的改进/估计(improvement/evaluation) 迭代。即给定一个初始策略，估计值函数，利用贪婪方法改进得到的策略，对改进后的策略进行估计……，最终得到最优策略${\pi }^{\ast }$和最优状态价值函数$v^{\ast }$
• 这种方法总能收敛到最佳策略${\pi }^{\ast }$

（2）策略改善

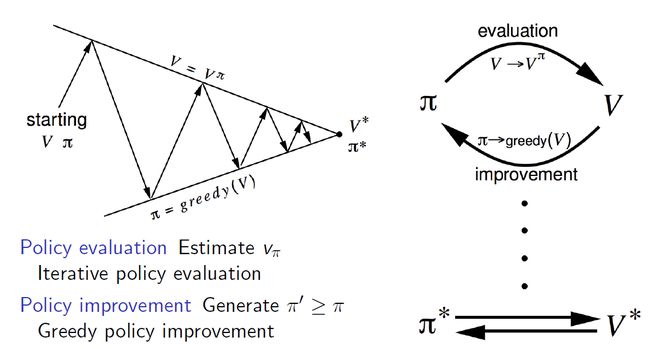
方法：
策略评估：求$v_{\pi }$，使用迭代策略评价
策略改善： 提升策略${\pi }^{\prime }\ge \pi$，使用贪婪策略提升
解释：
随机初始化一个$V$和$\pi$，通过测量评价求得当前策略下的价值函数$V^{\pi }$，然后做一次贪婪的策略提升${\pi }^{\prime }=greedy(V)$，此时的价值函数$V^{\pi }$就不是基于当前策略${\pi }^{\prime }$，再做一次策略评价，使得$V^{{\pi }^{\prime }}$与当前策略${\pi }^{\prime }$一致……反复多次，最终得到最优策略${\pi }^{\ast }$和最优状态价值函数$V^{\ast }$
Ⓜ本质：
使用当前策略产生新的样本，然后使用新的样本更好的估计策略的价值，然后利用新的价值更新策略，不断重复。理论可以证明最终策略将收敛到最优。

（3）举例——连锁汽车租赁

Jack有两个租车点（1号租车点和2号租车点）提供汽车租赁，由于不同的店车辆租赁的市场条件不一样，为了能够实现利润最大化，每天夜里，Jack可以在两个租车点间进行车辆调配，以便第二天能最大限度的满足两处汽车租赁服务。

• 已知条件
  • 状态空间$S$：1号租车点和2号租车点，每个地点最多20辆车供租赁。
  • 动作空间$A$：每天下班后最多转移5辆车从一个租车点到另一个租车点。
  • 转移概率$P$：租出去的车辆数量和归还的车辆数量是随机的，但满足泊松分布$\frac{{\lambda }^n}{n!}{e}^{-\lambda }$
    • 1号租车点，$\lambda =3$，每天租车请求3次，归还3次
    • 2号租车点，$\lambda =4$，每天租车请求4次，归还2次
  • 即时奖励$R$：Jack每租出去一辆车可以获利10美金，但必须是有车可租的情况，不考虑在两地转移车辆的支出。
  • 衰减系数$\gamma$：0.9。
• 问题
  • 最优的策略是什么
• 求解
  • 思路
    • 从某一个策略出发开始迭代，如不移动车辆。以此作为给定策略进行价值迭代，当迭代收敛到一定程度后，改善策略，随后再次迭代，如此反复，直至最终收敛
  • 分析
    • 每个租车点最多20辆车，状态数量是$21\times 21=441$个
    • 最多调配5辆车，动作集合$A=\{(-5,5),(-4,4),\dots ,(0,0),(1,-1),\dots (5,-5)\}$ 11种情况，每个元素表示(1号出入车辆，2号出入车辆)，正负分别表示入和出。
  • 核心
    • 根据泊松分布确定各状态的即时奖励，进而确定每个状态的价值。
      

（4）策略评估和策略改善的算法流程

策略改善：是将已有的策略$\pi (S,A)$和价值函数矩阵V带入，与最优值比较，从而更新策略为最优

• 初始化Q矩阵，将计算好的V矩阵和策略$\pi (S,A)$带入状态循环中，每个状态计算一遍
• 将当前状态转变为1号和2号租车点的保有车辆数
• 带入动作集合，计算找出可能的未来状态S’与可执行的动作possible action
• 计算Q矩阵：$Q(S,PossibleAction)=R_1(S^{\prime })+R_2(S^{\prime })-2Cost(PossibleAction)+\gamma V(S^{\prime })$
• 用策略$\pi (S,A)$与$Q_{m}ax$所在的动作进行比较，若是不符合则令flag：Policy_Stable=False
  策略评估+策略改善：
• 计算奖励矩阵，初始化Q矩阵和V矩阵
• 判断Policy_Stable是否为False，如果True则输出结果$\pi (S,A)$，否则进入迭代循环过程
• 令Policy_Stable=True
• 执行策略评估算法
• 执行策略改善算法，得到Policy_Stable的结果，返回第二步

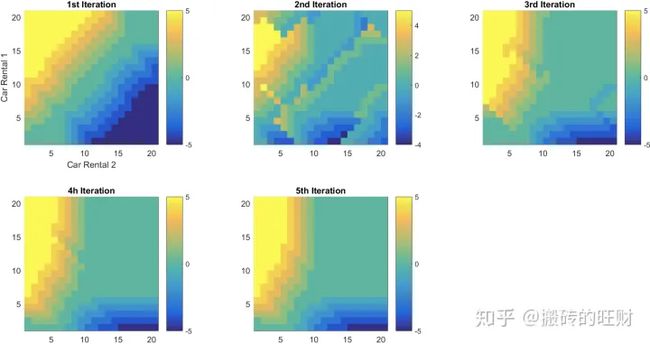
结果与评价：
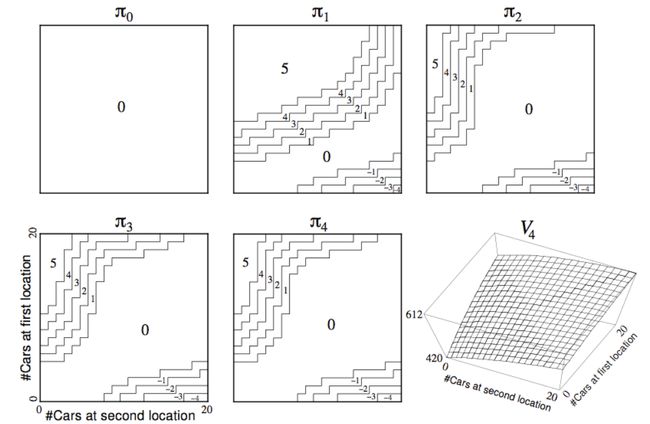
下面这幅图表示出了Policy-Improvement策略进化的过程，直到第5次迭代，动作策略最终稳定为最优策略。
（横轴表示2号租车点的车辆保有量，纵轴表示1号租车点的车辆保有量，图上的颜色由蓝到绿到黄表示了车辆调配的策略，正负号分别表示从1号调出车辆到2号，从2号调出车辆到1号。）

（5）策略改善的理论证明

• 考虑一个确定的策略：$a=\pi (s)$
• 通过贪婪计算优化策略：${\pi }^{\prime }=\arg \underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)$，注意这里使用的是动作价值函数
• 相当于用1步迭代改善状态 s 的 q 值。即在当前策略下，状态s在动作${\pi }^{\prime }(s)$下得到的q值$q_{\pi }(s,{\pi }^{\prime }(s))$，等于当前策略下所有可能动作得到的q值中的最大值$\arg \underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)$，这个值不小于当前策略$\pi$给出行为$\pi (s)$的q值$v_{\pi }(s)$：$$q_{\pi }(s,{\pi }^{\prime }(s))=\underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)\ge q_{\pi }(s,\pi (s))=v_{\pi }(s)$$
• 该式子说明，如果q值不再改善，则某一状态下，遵循当前策略给定行为得到的q值将是最优策略下所能得到的最大q值：$$q_{\pi }(s,{\pi }^{\prime }(s))=\underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)=q_{\pi }(s,\pi (s))=v_{\pi }(s)$$
• 因此满足Bellman最优方程$v_{\pi }(s)=\arg \underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)$，说明当前策略下的状态价值就是最优状态价值
• 对于所有的状态$s\in S$，都满足$v_{\pi }(s)=v_{\ast }(s)$，因此$\pi$是最优策略
• 策略提升定理$v_{\pi }(s)\le v_{{\pi }^{\prime }}(s)$的证明：
  

注意：大写的$V(s)$函数表示估计值，小写的$v(s)$表示真实值

（6）策略迭代的扩展

1)修饰过的策略迭代（Modified Policy Iteration）

❓问题引入：

• 很多时候，策略的更新较早就收敛到最优策略，而状态价值的收敛要慢很多。➡是否有必要一直迭代计算直到状态价值收敛
• 策略迭代在每一个迭代步总是先对策略进行值函数，直到收敛➡考虑能否在策略估计未收敛时就进行策略改进？
  解决：
• 有时候不需要持续迭代至有最优价值函数，可以设置一些条件提前终止迭代
• 比如，引入epsilon收敛，比较两次迭代的价值函数平方差、直接设置迭代次数、每迭代一次更新一次策略等
• 比如简单地在对策略估计迭代k次后就进行策略改进（k=1的情形就是值迭代方法）

2)广义策略迭代（Generalised Policy Iteration）

☀策略迭代包括两个同时进行的交互过程：

• 使得值函数（value function）与当前策略一致（策略评价 policy evaluation）
• 使得策略相对于当前值函数较贪婪（策略提升 policy improvement）

☀常规做法：

• 在策略迭代中，这两个过程交替进行，每个过程在另一个过程开始之前完成

❗问题：这不是必需的

举例

• 值迭代（value iteration）中，在每个策略提升（policy improvement）之间仅执行一次策略评估（policy evaluation）迭代
• 在异步（asynchronous）动态规划时，评价和提升过程则以更精细的方式交错。
• 只要两个过程都持续更新所有的状态，那么最终结果通常是相同的——收敛到最优值函数和最优策略

广义策略迭代（Generalized Policy iteration，GPI）

• 指代让策略评价和策略提升交互的一般概念，而不依赖于两个过程的粒度（granularity）和其他细节
• 几乎所有强化学习方法都可以被很好地描述为GPI。也就是说，它们都具有可识别的策略 π （identifiable policy）和值函数 V。
• 策略 π 总是相对于值函数 V 被改善

the policy always being improved with respect to the value function

• 值函数V 总是趋向策略 π下的值函数 Vπ

the value function always being driven toward the value function for the policy

• 如果评价过程和提升过程都稳定下来，不再发生变化，则值函数和策略必须都是最优的，即贝尔曼方程成立：$$v_{\ast }(s)=\underset{a}{\max }\mathbb{E}[R_{t+1}+\gamma v_{\ast }(S_{t+1}|S_t=s,A_t=a)]=\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\ast }(s^{\prime })]$$
  

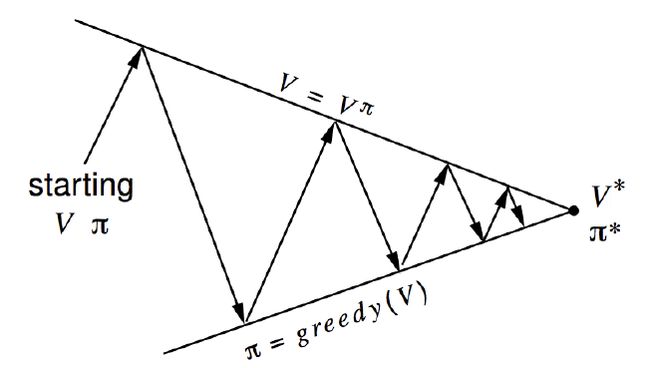
可以用两个目标来考虑GPI中评价和提升过程的相互作用

• 上面的线代代表目标 $v=v_{\pi }$，下面的线代表目标 $\pi =greedy(v)$。
• 目标会发生相互作用，因为两条线不是平行的。
• 从一个策略 π 和一个价值函数 v 开始，
  • 每一次箭头向上代表着利用当前策略进行值函数的更新，每一次箭头向下代表着根据更新的值函数贪婪地选择新的策略，即每次都采取转移到可能的、状态函数最高的新状态的行为。
• 最终将收敛至最优策略和最优值函数。

4.值迭代

（1）MDP中的值迭代

1)最优化原则 Principle of Optimality

任何一个最优策略都可以被分为两部分：

• 从状态 $s$ 到后继状态 $s^{\prime }$ 采取最优的初始动作 $A_{\ast }$
• 在后继状态 $s^{\prime }$ 开始沿着最优策略继续进行

一个策略 $\pi (a|s)$能够使得状态 s 获得最优价值 $v_{\pi }(s)=v_{\ast }(s)$，当且仅当： 对于从状态 s 可以到达的任何状态 s′， π 从状态 s′ 中能够获得最优价值 ，即 $v_{\pi }(s^{\prime })=v_{\ast }(s^{\prime })$

2)确定性的价值迭代

在上一个定理的基础上，如果我们知道期望的最终位置和明确的状态间关系，可以认为是一个确定性的价值迭代。即，把问题分解成一些子问题，从最终目标开始分析往回推，直到推完所有状态：

• 知道子问题的解$v_{\ast }(s^{\prime })$
• 可以通过one-step lookahead得到前一个状态的解$$v_{\ast }(s)\leftarrow \underset{a\in A}{\max }[R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{S{S}^{\prime }}^a{v}_{\ast }(s^{\prime })]$$
  • $[R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{S{S}^{\prime }}^a{v}_{\ast }(s^{\prime })]$代表进行了一步迭代式策略评价
  • $max$代表进行了一次策略提升
    注意：
• 这里直接用值函数进行迭代，不涉及策略
• 也适用于循环的随机MDPs

3)举例——最短路径

（a）已知条件

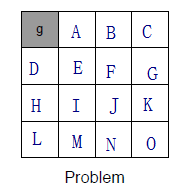
g点处的reward=0，其余状态均reward=1

（b）问题

如何在一个$4\times 4$的方格世界中，找到任一一个方格到最左上角方格的最短路径

（c）求解思路

解决方案1：确定性的价值迭代
左上角g为最终目标，与左上角相邻的两个方格A和D开始计算，因为这两个方格是可以仅通过1步就到达目标状态的状态，或者说目标状态是这两个状态的后继状态。

• 对A来说，向左可以到达终点获得reward，向右则没有奖赏。所以根据公式中的max，A就会选择左走，它的 V 值最大。第一次迭代A就已经可以获得最大值。
• 对B来说，第一次迭代向左和向右都一样，但是在第二次迭代中就会发现两次向左就可以达到最大值。这就是值迭代的过程。
  解决方案2：价值迭代

• 并不确定最终状态在哪里，而是根据每一个状态的最优后续状态价值来更新该状态的最佳状态价值，这里强调的是每一个。

• 多次迭代最终收敛。
• 这也是根据一般适用性的价值迭代。在这种情况下，就算不知道目标状态在哪里，这套系统同样可以工作。

（d）求解过程

• 首先初始化每个状态（即从A到O）的 V 都为0
• 第一次迭代，k=1
  • $V_2(s)={\max }_{a\in A}[R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{S{S}^{\prime }}^a{V}_1(s^{\prime })]=-1$，这里所有的$V_1(s)=0$，因此max都是一样的，所有的$V_2(s)=-1$
• 第二次迭代，k=2
  • $V_3(s)={\max }_{a\in A}[R_s^a+\gamma {\sum }_{s^{\prime }\in S}{P}_{S{S}^{\prime }}^a{V}_2(s^{\prime })]=-1$
    • 对于A来说，$V_3(A)=\underset{a=\uparrow \downarrow \leftarrow \to }{\max }\{(R_A^{\uparrow }+\gamma P_{AA}^{\uparrow }{V}_2(A)),(R_A^{\downarrow }+\gamma P_{AE}^{\downarrow }{V}_2(E)),(R_A^{\leftarrow }+\gamma P_{Ag}^{\leftarrow }{V}_2(g)),(R_A^{\to }+\gamma P_{AB}^{\to }{V}_2(B))\}=-1$
    • 对于B来说，$V_3(B)=\underset{a=\uparrow \downarrow \leftarrow \to }{\max }\{(R_B^{\uparrow }+\gamma P_{BB}^{\uparrow }{V}_2(B)),(R_B^{\downarrow }+\gamma P_{BF}^{\downarrow }{V}_2(F)),(R_B^{\leftarrow }+\gamma P_{BA}^{\leftarrow }{V}_2(A)),(R_B^{\to }+\gamma P_{BC}^{\to }{V}_2(C))\}=-2$
• 继续迭代，直到每个状态的累积奖赏都不变

4)值迭代 Value Iteration

• 问题
  • 寻找最优策略 π。
• 解决方案
  • 从初始状态价值开始同步迭代计算，最终收敛，整个过程中没有遵循任何策略。
    注意：
• 与策略迭代一样的是，价值迭代最终也同样收敛到最优值函数
• 与策略迭代不一样的是，价值迭代没有显式的策略，它通过贝尔曼最优方程，隐式地实现了策略改进这一步（固定选择greedy，通过greedy得到的策略通常为确定性策略）
• 中间过程中的价值函数可能并不对应于任何策略

价值迭代虽然不需要策略参与，但仍然需要知道状态之间的转移概率，也就是需要知道模型

（2）DP算法的总结

• 值迭代
  • $v_1\to v_2\to \dots \to v_{\ast }$
  • 没有显示的策略，在迭代过程中值函数可能不对应任何策略
  • 使用贝尔曼最优方程，效率较高
• 策略迭代
  • ${\pi }_1\to v_1\to {\pi }_2\to v_2\to \dots \to {\pi }_{\ast }\to v_{\ast }$
  • 有显示的策略，在迭代过程中值函数对应某个具体的策略
  • 使用贝尔曼期望方程+贪婪策略提升，效率较低
    | 问题 | 贝尔曼方程 | 算法 |
    | ---- | --------------------------- | -------------- |
    | 评价 | 贝尔曼期望方程 | 迭代式策略评价 |
    | 优化 | 贝尔曼最优方程 | 值迭代 |
    | 优化 | 贝尔曼期望方程+贪婪策略提升 | 策略迭代 |
    注意：
• 算法都是基于状态值函数的（$v_{\pi }(s)$或$v_{\ast }(s)$）
• 如果一共有m个动作，n个状态，则每次迭代的复杂度为$O(m{n}^2)$
• 上述算法也可以扩展到基于动作价值函数（$q_{\pi }(s,a)$或$q_{\ast }(s,a)$），此时每次迭代的复杂度为$O(m^2{n}^2)$

预测问题：

• 在给定策略下迭代计算价值函数，运用贝尔曼期望方程，通过迭代法策略评估
  控制问题：
• 策略迭代寻找最优策略问题则先在给定或随机策略下计算状态价值函数，根据状态函数贪婪更新策略，多次反复找到最优策略
• 单纯使用价值迭代，全程没有策略参与也可以获得最优策略，但需要知道状态转移矩阵，即状态 s 在行为 a 后到达的所有后续状态及概率

5.动态规划的扩展

前面介绍的都是同步动态规划，即每次迭代都会同时保存所有状态。

（1）异步动态规划

1)定义

异步动态规划将所有的状态，以任意顺序独立进行备份保存。
异步动态规划可以减少计算量，但如果要收敛，必须保证任一时刻任何状态都能被选中。

• 可以任意挑选任何state，并将该state进行备份。可以立即行动，立即插入新的value函数，它会在底部进行备份，不需要等待全部状态更新完。
• 更新的是单一状态，而不是整个动作空间。
• 在最短路径例子中，每次迭代都需要计算A-O的所有状态的v值，异步动态规划可以只计算某个状态的v值

2)原位动态规划 In-place DP

直接原地更新下一个状态的$v$值，不像同步迭代一样额外存储新的状态$v$值。此时，重要的是按何种次序更新状态价值。

• 同步值迭代存储了两个值函数：
  

$$

• 原位就地动态规划仅存储一个值函数，一个状态更新了一侧值函数后，在更新它的后继状态时直接使用最新的值函数：$$v(s)\leftarrow \underset{a\in \mathcal{A}}{\max }({\mathcal{R}}_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{S{S}^{\prime }}^{a}v(s^{\prime }))$$

3)重要状态优先更新 Prioritised sweeping

优先更新重要的状态

• 使用贝尔曼误差来确定状态的重要性：$$|\underset{a\in \mathcal{A}}{\max }\left({\mathcal{R}}_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{S{S}^{\prime }}^{a}v(s^{\prime }))\right)-v(s)|$$
• 贝尔曼误差反映了当前状态价值与更新后状态价值的绝对值，贝尔曼误差越大，越有必要优先更新。
• 这种算法使用优先级队列能够有效实现
• 备份贝尔曼误差最大的状态
• 每次备份后，更新受到影响的状态的贝尔曼误差
  • 受到影响的状态：
    • 更新的状态作为$s$，贝尔曼误差变为0，排到优先级队列的队尾
    • 更新的状态作为前驱状态$s^{\prime }$，要求知道逆运动学（状态转移矩阵是正运动学，已知当前状态求前驱状态是逆运动学）
• 可以保证每个状态都能被遍历，因此能收敛
  • 任意状态被更新后都排到队尾，此时它的贝尔曼误差清零，只有所有状态都更新完它才会作为一个前驱状态

4)实时动态规划 Real-Time DP

选择那些agent真正访问过的state，并不是简单的扫描所有东西。实际上，是在真实环境中运行一个agent，搜集真正的样本，使用来自某个轨迹的真正的样本。

• 只更新那些与个体关系密切的状态
• 使用个体经验来指导更新状态的选择
  • 有些状态虽然理论上存在，但在现实中几乎不会出现。利用已有现实经验。
• 在每个时间步$S_t,A_t,R_{t+1}$后，存储备份状态$S_t$：$$v(S_t)\leftarrow \underset{a\in \mathcal{A}}{\max }({\mathcal{R}}_{S_t}^a+\gamma \sum _{s^{\prime }\in S}{P}_{S_t{s}^{\prime }}^{a}v(s^{\prime }))$$
  • St是实际与Agent相关或者说Agent经历的状态，可以省去关于那些仅存在理论上的状态的计算。

（2）全宽备份和示例备份

1)全宽备份

• DP使用full-width备份
• 对于每个备份（同步或异步）
  • 每个后继的状态和动作都被考虑
  • 需要已知MDP转移矩阵$\mathcal{P}$和奖励函数$\mathcal{R}$➡因此DP面临维度灾难问题
• 维度灾难问题
  • DP对中等规模的问题（数百万个状态）有效
  • 对于大问题，DP受到贝尔曼的维数诅咒
    • 状态数随状态变量数呈指数增长
  • 即使一次备份也可能太昂贵
  • 解决方法：采样更新 Sample Backups
    

2)采样更新Sample Backups

利用样本进行备份

• 实现
  • 通过采样得到转移记录transition
  • 通过采样代替总体
• 优点
  • 无模型Model-free：不需要完整掌握MDP的条件，无需知道转移矩阵$\mathcal{P}$和奖励函数$\mathcal{R}$
  • 避免了维数灾难的问题
  • backup的时间复杂度固定，与状态数$n$无关

（3）近似动态规划 Approximate

使用其他技术手段（例如神经网络）建立一个参数较少，消耗计算资源较少、同时虽然不完全精确但却够用的近似价值函数：

• 近似值函数
• 使用函数逼近器$\hat{v}(s,W)$
• 将动态规划应用于$\hat{v}(\cdot ,W)$
• 例如:拟合值迭代在每个迭代k重复一次，
  • 样本状态 $\tilde{S}\subseteq S$
  • 对于每个状态$s\in \tilde{S}$，使用Bellman最优方程估算目标值：$${\tilde{v}}_k(s)=\underset{a\in \mathcal{A}}{\max }({\mathcal{R}}_{S_t}^a+\gamma \sum _{s^{\prime }\in S}{P}_{S_t{s}^{\prime }}^a\hat{v}(s^{\prime },w_k))$$
  • 使用目标$\{⟨s,{\tilde{v}}_k(s)⟩\}$训练下一个值函数$\hat{v}(\cdot ,w_{k+1})$

6.压缩映射

• 技术问题
• 如何知道值迭代收敛到 v∗ ？
• 迭代式策略评价收敛到 vπ ？
• 策略迭代收敛到 v∗ ？
• 解是唯一的吗？
• 算法收敛速度？