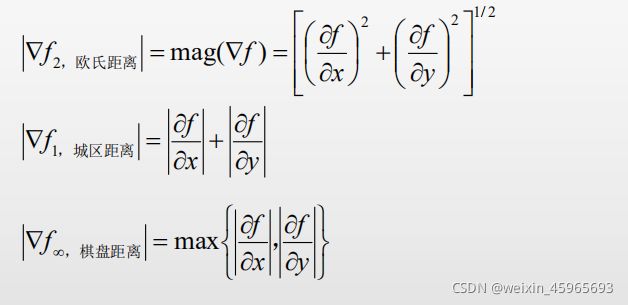数字图像处理-第二周-理论课
第三章空间域的图像增强
学习灰度图像变换、直方图、空间域平滑及锐化滤波等内容
- 掌握图像的均衡化方法、空域的线性和非线性滤波器的用法。
- 理解图像亮度变换函数的原理、了解图像与处理的常用方法。
- 基本的灰度变换方法、图像的均衡化、线性和非线性滤波器的用法
- 各种滤波函数的选择和用法
1.概述
噪声分类:
加性噪声:和图像信号强度不相关
乘性噪声:和图像信号是相关的
椒盐噪声:黑图像上的白点,白图像上的黑点
量化噪声:是由量化引起的
图像间的运算
算术运算:加减乘除
逻辑运算:与或非异或
加操作的去噪效果:
假设 g ( x , y ) g(x,y) g(x,y)是在 f ( x , y ) f(x,y) f(x,y)基础上叠加了一个加性噪声 g ( x , y ) = f ( x , y ) + η ( x , y ) g(x,y)=f(x,y)+\eta(x,y) g(x,y)=f(x,y)+η(x,y)
则叠加K次观测图像后 g ˉ ( x , y ) = 1 K ∑ i = 1 K g i ( x , y ) \bar g(x,y)=\frac{1}{K}\sum_{i=1}^{K}g_{i}(x,y) gˉ(x,y)=K1∑i=1Kgi(x,y)
其期望为 E g ˉ ( x , y ) = f ( x , y ) E{\bar g(x,y)}=f(x,y) Egˉ(x,y)=f(x,y)
方差和标准差分别为 σ g ˉ ( x , y ) 2 = 1 K σ η 2 ( x , y ) , σ g ˉ ( x , y ) = 1 K σ η ( x , y ) \sigma^{2}_{\bar g(x,y)}=\frac{1}{K}\sigma^2_{\eta}(x,y),\sigma_{\bar g(x,y)}=\frac{1}{\sqrt{K}}\sigma_{\eta}(x,y) σgˉ(x,y)2=K1ση2(x,y),σgˉ(x,y)=K1ση(x,y)
标准差随叠加的次数而减小,说明有去噪效果
减操作用于增强差异,目的:图像差异、边缘检测、运动目标信息检测
使用相乘和相除来校正阴影
2.灰度变换方法
通过改变像素的灰度实现
g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)]
变换中对每一个点做相同的处理(点处理)
T变换函数,可以解析形式或函数曲线
图像求反,L图像最大灰阶
g ( x , y ) = L − f ( x , y ) g(x,y)=L-f(x,y) g(x,y)=L−f(x,y)

增强对比度,灰度级拉伸。增强原图像各部分之间的反差
g ( x , y ) = { ( c / a ) f ( x , y ) 0 ≤ f ( x , y ) ≤ a [ ( d − c ) / ( b − a ) ] f ( x , y ) + c a ≤ f ( x , y ) ≤ b ( ( M g − d ) / ( M f − b ) ] [ f ( x , y ) − b ] + d b ≤ f ( x , y ) ≤ M f g(x, y)=\left\{\begin{array}{ll} (c / a) f(x, y) & 0 \leq f(x, y) \leq a \\ {[(d-c) /(b-a)] f(x, y)+c} & a \leq f(x, y) \leq b \\ \left(\left(M_{g}-d\right) /\left(M_{f}-b\right)\right][f(x, y)-b]+d & b \leq f(x, y) \leq M_{f} \end{array}\right. g(x,y)=⎩⎨⎧(c/a)f(x,y)[(d−c)/(b−a)]f(x,y)+c((Mg−d)/(Mf−b)][f(x,y)−b]+d0≤f(x,y)≤aa≤f(x,y)≤bb≤f(x,y)≤Mf
对数变换,借助对数变换曲线实现动态范围压缩
g ( x , y ) = a + b l o g [ f ( x , y ) + 1 ] g(x,y)=a+blog[f(x,y)+1] g(x,y)=a+blog[f(x,y)+1]
幂次变换(伽马校正),用幂次变换进行对比度增强
s = c r γ s=cr^{\gamma} s=crγ
当 γ < 1 \gamma<1 γ<1时,扩展低亮度区、压缩高亮度区,突出暗区域细节
当 c = γ = 1 c=\gamma=1 c=γ=1时,扩展低亮度区、压缩高亮度区
当 γ > 1 \gamma>1 γ>1时,压缩低亮度区、扩展高亮度区
分段线性变换函数,不同的分段函数达到不同的效果
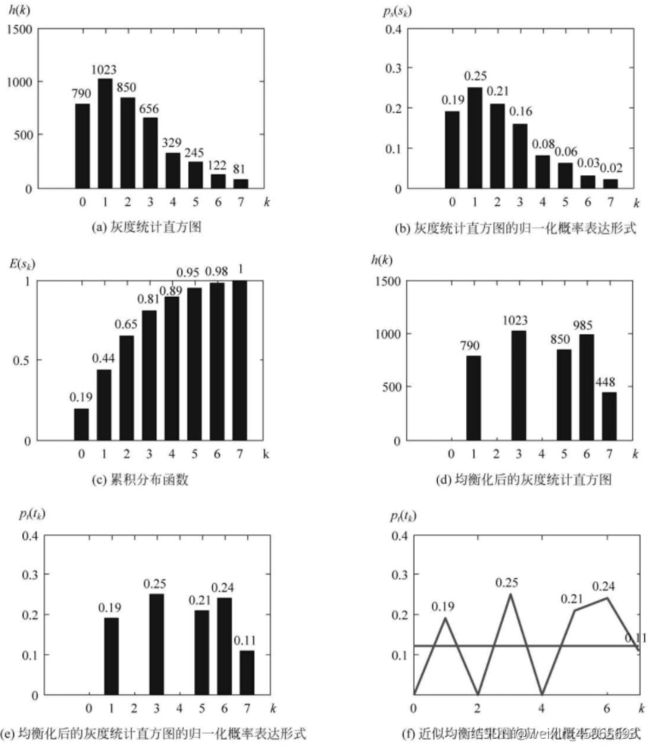
3.直方图均衡化
直方图均衡化:借助直方图变换实现灰度映射
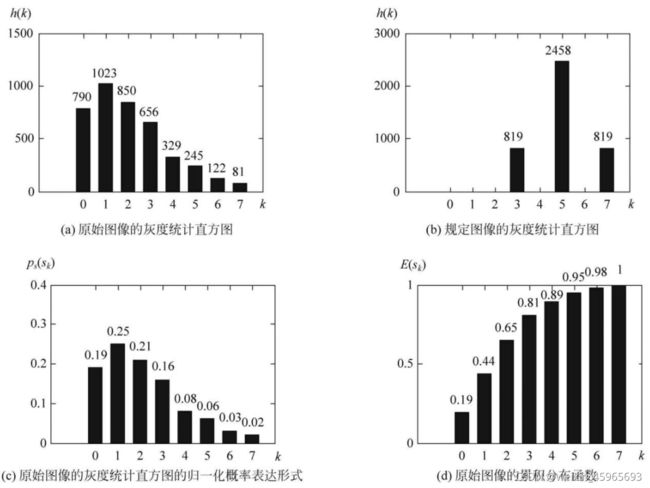
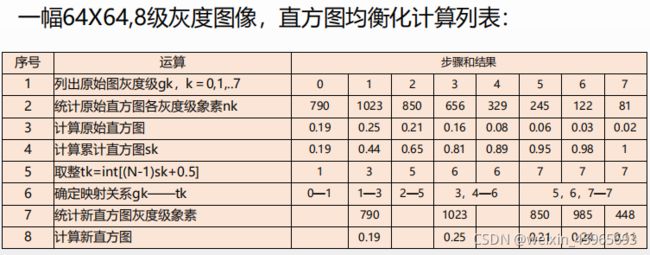
直方图:数字图像中每一灰度级与其出现的频度之间的关系,某一灰度的像素数与总像素数之比。
P f ( f k ) = n k N k = 0 , 1 , 2 , . . . , L − 1 P_{f}(f_{k})=\frac{n_{k}}{N}\quad k=0,1,2,...,L-1 Pf(fk)=Nnkk=0,1,2,...,L−1
其中,N为图像总的像素数目;nk为第k级灰度的像素数目,fk为第k级灰度值
- 直方图是统计概念,每一图像都有一个直方图,但一个直方图可以有完全不同的图像。
- 直方图只是统计特性,并不能反映与视觉感官一致的结果
- 直观上可以认为,如果一幅图像其像素占有全部可能的灰度级且分布均匀,则这样的图像有高对比度和多变的灰度色调
- 通一幅图像不同的处理,对应于不同的直方图,通过直方图可以从统计意义上了解图像的质量
直方图拉伸
直方图平移
直方图均衡化:原始直方图变为均匀形式,使图像的熵最大,图像包含的平均信息量最大。
s k = ∑ j = 0 k n j N = ∑ j = 0 k P ( f j ) k = 0 , 1 , 2 , . . . , L − 1 s = T ( r ) 0 ≤ r ≤ 1 s_{k}=\sum_{j=0}^{k}\frac{n_{j}}{N}=\sum_{j=0}^{k}P(f_{j})\quad k=0,1,2,...,L-1\\s=T(r)\quad 0\leq r\leq 1 sk=j=0∑kNnj=j=0∑kP(fj)k=0,1,2,...,L−1s=T(r)0≤r≤1
n j n_{j} nj是输入图像中灰度级为j级灰度的像数个数,N是图像中像数的总数, s k s_{k} sk是图像的累积直方图。数字图像的灰度级范围为 [ 0 , L − 1 ] [0,L-1] [0,L−1]
考虑连续函数,并让变量r代表增强图像的灰度级。假设r被归一化到区间 [ 0 , L − 1 ] [0,L-1] [0,L−1]内。对于任意一个满足上述条件的r,我们注意以下变换形式,在原始图像中,对于每一个像素值r产生一个灰度值s。
显然可以假设变换函数 T ( r ) T(r) T(r)满足以下条件
(1)在区间[0,1]中为单值且单调递增
(2) 0 ≤ T ( r ) ≤ 1 0\leq T(r)\leq 1 0≤T(r)≤1
可以证明累积分布函数满足上述两个条件,并能将r的分布变换为均匀分布
相同场景的不同设备产生的图像,在直方图均衡化后会趋同。
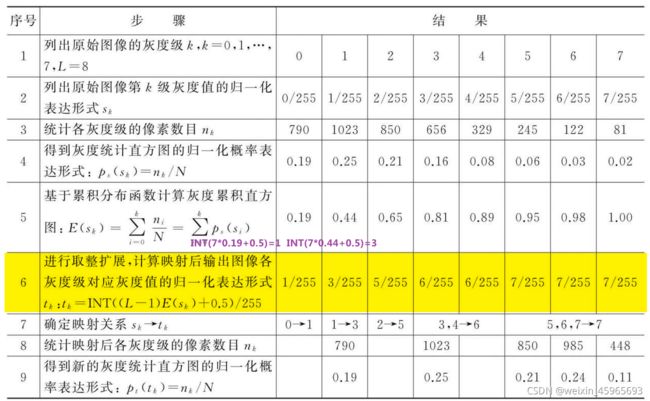
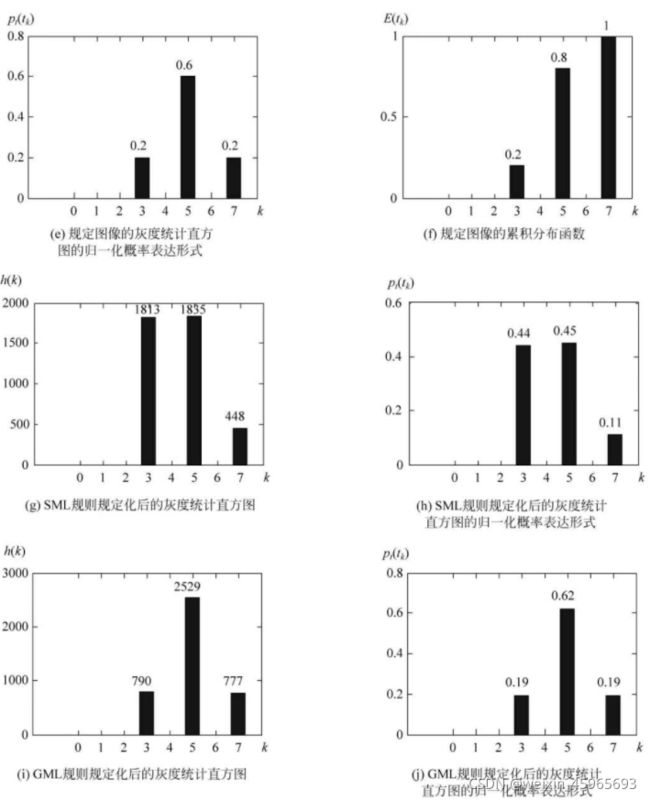
直方图规定化(匹配):可以指定处理的图像具有所希望的直方图形状
直方图均衡化可以自动增强整个图像对比度,但增强效果不容易控制。实际中有时需要把直方图换成规定形式。主要步骤:
对原始直方图进行灰度均衡化
t k = ∑ i = 0 k p s ( s i ) , k = 0 , 1 , 2 , . . . , M − 1 t_{k}=\sum_{i=0}^{k}p_{s}(s_{i}),k=0,1,2,...,M-1 tk=i=0∑kps(si),k=0,1,2,...,M−1
对规定直方图进行均衡化
v l = ∑ j = 0 l p u ( u j ) , l = 0 , 1 , 2 , . . . , N − 1 v_{l}=\sum_{j=0}^{l}p_{u}(u_{j}),l=0,1,2,...,N-1 vl=j=0∑lpu(uj),l=0,1,2,...,N−1
将原始直方图对应映射到规定的直方图
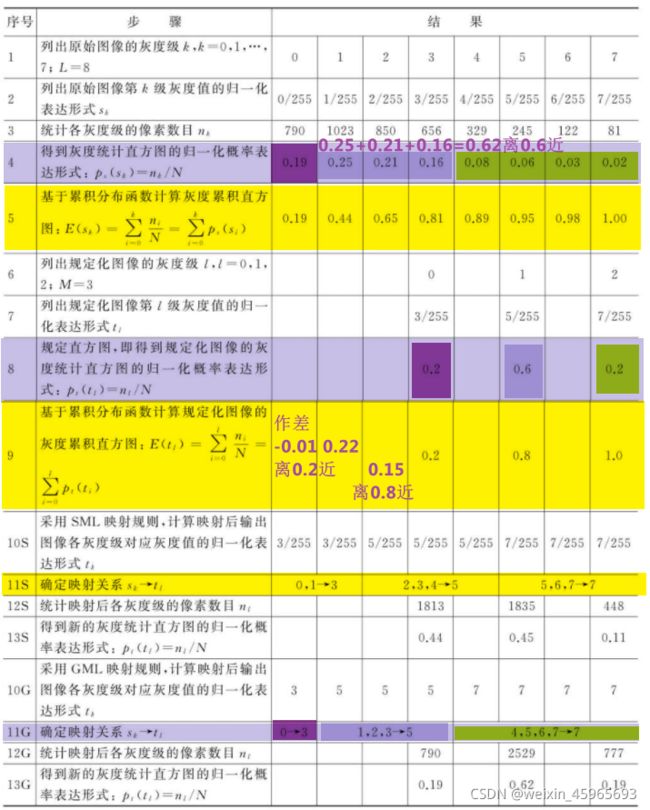
灰度映射规则是直方图规定化的关键。由于存在取整误差的影响,灰度映射规则的好坏在离散空间尤其重要。常用的灰度映射规则包括单映射规则(SML)和组映射规则(GML)。
寻找k,l式式子最小,然后将 P s ( s i ) P_{s}(s_{i}) Ps(si)对应到 P u ( u j ) P_{u}(u_{j}) Pu(uj)中,由于每个 P s ( s j ) P_{s}(s_{j}) Ps(sj)分别对应称为单映射
∣ ∑ i = 0 k p s ( s i ) − ∑ j = 0 l p u ( u j ) ∣ k = 0 , 1 , 2 , . . . , M − 1 l = 0 , 1 , 2 , . . . , N − 1 |\sum_{i=0}^{k}p_{s}(s_{i})-\sum_{j=0}^{l}p_{u}(u_{j})|\\k=0,1,2,...,M-1\\l=0,1,2,...,N-1 ∣i=0∑kps(si)−j=0∑lpu(uj)∣k=0,1,2,...,M−1l=0,1,2,...,N−1
组映射规则
设有一整数函数 I ( l ) i = 0 , 1 , 2 , 3 , M − 1 I(l)\quad i=0,1,2,3,M-1 I(l)i=0,1,2,3,M−1满足 0 < I ( 0 ) < I ( 1 ) < . . . < I ( N − 1 ) < M − 1 0
∣ ∑ i = 0 I ( l ) p s ( s i ) − ∑ j = 0 l p u ( u j ) ∣ k = 0 , 1 , 2 , . . . , M − 1 l = 0 , 1 , 2 , . . . , N − 1 |\sum_{i=0}^{I(l)}p_{s}(s_{i})-\sum_{j=0}^{l}p_{u}(u_{j})|\\k=0,1,2,...,M-1\\l=0,1,2,...,N-1 ∣i=0∑I(l)ps(si)−j=0∑lpu(uj)∣k=0,1,2,...,M−1l=0,1,2,...,N−1
如果 l = 0 l=0 l=0,则将i从0到I(0)的 P s ( s j ) P_{s}(s_{j}) Ps(sj)对应到 P u ( u j ) P_{u}(u_{j}) Pu(uj)去
如果 l ≥ 1 l\geq 1 l≥1则将i从 I ( l − 1 ) + 1 I(l-1)+1 I(l−1)+1到 I ( l ) I(l) I(l)的 P s ( s j ) P_{s}(s_{j}) Ps(sj)对应到 P u ( u j ) P_{u}(u_{j}) Pu(uj)去
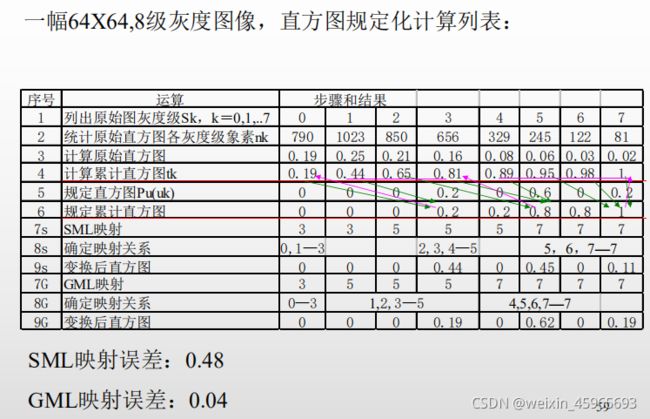
- 单映射属于有偏映射,组映射是统计无偏
- 组映射结果更接近规定的直方图
- 组映射的期望误差总是小于或等于单映射误差
- 当规定直方图与原始直方图灰度级相等时,SML和GML相同
4.空域滤波器
空域滤波基础
空域模板邻域操作完成
分类:
特点分:线性、非线性
功能分:平滑、锐化
平滑:模糊、消除噪声;减弱或消除傅里叶高频分量
锐化:增强细节、边缘;减弱或消除傅里叶低频分量
邻域计算:算术运算和逻辑运算都可用于邻域运算,主要以模板形式运算。
模板运算:将赋予某个像素的值作为它本身灰度值和其相邻像素灰度值的函数。通过改变模板系数可以达到不同图像处理效果。
平滑空间滤波器
线性空间平滑滤波器
常用模板
H 1 = 1 9 [ 1 1 1 1 1 1 1 1 1 ] H 2 = 1 10 [ 1 1 1 1 2 1 1 1 1 ] H [ 3 = 1 16 [ 1 2 1 2 4 2 1 2 1 ] H_{1}=\frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]\quad H_{2}=\frac{1}{10}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{array}\right]\quad H_{[3}=\frac{1}{16}\left[\begin{array}{lll} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array}\right] H1=91⎣⎡111111111⎦⎤H2=101⎣⎡111121111⎦⎤H[3=161⎣⎡121242121⎦⎤
非线性空间平滑滤波器
统计排序滤波器是一种非线性的空间滤波器,它的响应基于图像滤波器包围的图像区域中像素的排序,然后由统计排序结果决定的值代替中心像素的值。
中值滤波器是将像素邻域内灰度的中间值代替该像素的值。中值滤波器对处理脉冲噪声(椒盐噪声)非常有效。
特点:保边缘、非线性、频谱基本不变

锐化空间滤波器
线性空间锐化滤波器
High boost=A×Original-Low pass=(A-1)×Original+High pass
A=1 普通高通滤波
A>1 高频增强
非线性空间锐化滤波器
基于一阶微分的图像增强——梯度法
二元函数 f ( x , y ) f(x,y) f(x,y)在坐标 ( x , y ) (x,y) (x,y)的梯度定义为一个二维列向量:
grad ( f ( x , y ) ) = ∇ f = ( ∂ f ∂ x ∂ f ∂ y ) T = ( G x G y ) T = ( G x G y ) \operatorname{grad}(f(x, y))=\nabla f=\left(\begin{array}{ll} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \end{array}\right)^{\mathrm{T}}=\left(\begin{array}{ll} G_{x} & G_{y} \end{array}\right)^{\mathrm{T}}=\left(\begin{array}{l} G_{x} \\ G_{y} \end{array}\right) grad(f(x,y))=∇f=(∂x∂f∂y∂f)T=(GxGy)T=(GxGy)
梯度的模有三种常用的非线性的定义方式: