数据结构与算法学习——动态规划-2

目录

博主介绍

个人主页:苏州程序大白
个人社区:CSDN全国各地程序猿
作者介绍：中国DBA联盟(ACDU)成员，CSDN全国各地程序猿（媛）聚集地管理员。目前从事工业自动化软件开发工作。擅长C#、Java、机器视觉、底层算法等语言。2019年成立柒月软件工作室，2021年注册苏州凯捷智能科技有限公司
如果文章对你有帮助，欢迎关注、点赞、收藏（一键三连）和C#、Halcon、python+opencv、VUE、各大公司面试等一些订阅专栏哦
有任何问题欢迎私信，看到会及时回复
微信号：stbsl6，微信公众号：苏州程序大白
想加入技术交流群的可以加我好友，群里会分享学习资料

前言

数据结构与算法学习——动态规划-1

继续数据结构与算法学习——动态规划-1继续讲解

1、最长连续递增序列

1、题目描述

给定一个未经排序的整数数组，找到最长且 连续递增的子序列 ，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有nums[i] < nums[i + 1]，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]]就是连续递增子序列。

• 示例一

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。 

• 示例二

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

2、解题思路

• 与最长递增子序列不同的是，最长连续递增序列要求连续，我们仍然可以延续之前的思路，对于下标为 i 的数组元素来说，如果它的前一个元素是一个最长连续递增序列的末尾且 nums[i - 1] < nums[i]，那么我们就可以将 nums[i] 拼接到 nums[i - 1] 的末尾，形成一个更长的连续序列。

• 确定 dp 数组中的含义。

dp[i] 表示以下标为 i 的数组元素为结尾的最长递增序列的长度。

• 确定状态转移方程。

对于 nums[i] 来说，如果nums[i - 1] < nums[i]，那么证明此时nums[i]可以拼接到以nums[i - 1]为结尾的最长连续递增序列中，此时递推公式应该为：

if (nums[i - 1] < nums[i]) {
	dp[i] = Math.max(dp[i], dp[i - 1] + 1);
}

• 初始化 dp 数组。

对于数组中的任何一个元素，我们都可以将其单独看为一个最长连续递增序列，所以我们需要将 dp 数组全部初始化为 1。

3、解题代码

public int findLengthOfLCIS(int[] nums) {
    if (nums == null || nums.length == 0) return 0;
    int[] dp = new int[nums.length];
    Arrays.fill(dp, 1);
    int max = 1;
    for (int i = 1;i < nums.length;i++) {
        if (nums[i - 1] < nums[i]) {
            dp[i] = Math.max(dp[i], dp[i - 1] + 1);
        }
        max = Math.max(dp[i], max);
    }
    return max;
}

1.1、最长重复子数组

1、题目描述

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

• 示例一

输入：
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3, 2, 1] 。

2、解题思路

• 确定 dp 数组的含义：

dp[i][j] 表示数组 nums1 下标范围为 [0, i - 1]的子数组与nums2下标为 [0, j - 1]的子数组的最长公共数组的长度。

• 确定状态转移方程：

对于上面提到的两个子数组，如果此时存在 nums1[i - 1] == nums2[j - 1] ，那么此时这两个子数组的最长公共长度就为 nums1[0: i - 2] 、 nums2[0: j - 2] 两个子数组的最长公共数组长度 + 1，即：

if (nums1[i - 1] == nums2[j - 1]) {
	dp[i][j] = dp[i - 1][j - 1] + 1;
}

• 初始化 dp 数组。

根据上面 dp 数组的定义，我们知道在 dp 数组中，dp[i][0] 和 dp[0][j] 是没有意义的，所以我们直接初始化为 0。

3、解题代码

public int findLength(int[] nums1, int[] nums2) {
    // base case 
    if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) return 0;
    // 创建一个 dp 数组，其中 dp[i]][j] 表示 nums1 中以 i - 1 下标为结尾的子数组 a ，nums2 中以 j - 1 下标为结尾的子数组 b ，ab 数组中最长公共子数组的长度
    int[][] dp = new int[nums1.length + 1][nums2.length + 1];
    // 使用一个全局变量保存最长公共子数组的长度
    int max = 0;
    // 这里的循环必须从 1 开始
    for (int i = 1;i <= nums1.length;i++) {
        for (int j = 1;j <= nums2.length;j++) {
            // 将两个子数组的结尾字符进行比较，如果结尾字符相等，那么进行状态转移
            if (nums1[i - 1] == nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            // 更新 max
            max = Math.max(max, dp[i][j]);
        }
    }
    return max;
}

1.2、最长公共子序列

1、题目描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是"abcde" 的子序列，但"aec"不是 "abcde" 的子序列。

• 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

• 示例一

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

• 示例二

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

2、解题思路

• 确定 dp 数组的含义。

和上一题一样，我们使用一个二维数组来解决这道题，其中 dp[i][j] 表示字符串 text1 以 i - 1 为结尾的子串与字符串 text2 以 j - 1 为结尾的子串之间最长公共子序列的长度。

• 确定状态转移方程。

在 LCS 问题中，我们设 text1 字符串的子串为 X = ，text2 字符串的子串为 Y = ，Z = 为它们的一个公共子序列，经过分析，有：

1、如果 xm == yn ，则 zk = xm = yn 且 Zk - 1 是 Xm - 1 与 Yn - 1 的一个 LCS （最长公共子序列）。

2、如果 xm != yn 且 zk != xm ，则 Zk 是 Xm - 1 与 Yn 的一个 LCS。

3、如果 xm != yn 且 zk != yn ，则 Zk 是 Yn - 1 与 Xm 的一个 LCS。

所以我们可以得到以下的状态转移方程。

if (xi == yj) {
	dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
	dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}

3、解题代码

public int longestCommonSubsequence(String text1, String text2) {
    if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) return 0;
    // 创建一个二维的 dp 数组
    int[][] dp = new int[text1.length() + 1][text2.length() + 1];
    // 进行循环，注意，循环应该从下标 1 开始
    for (int i = 1;i <= text1.length();i++) {
        for (int j = 1;j <= text2.length();j++) {
            // 同时这里比较的应该是 i - 1 与 j - 1 的字符，因为循环从 1 开始
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) { // 如果 i - 1 下标与 j - 1 下标的字符相同
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else { // 如果 i - 1 下标与 j - 1 下标的字符不相同
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    // 返回 dp[text1.length()][text2.length()] 即可，这个值代表 text1 字符串与 text2 字符串之阿的最长公共子序列的长度
    return dp[text1.length()][text2.length()];
}

1.3、 不相交的线

1、题目描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

• nums1[i] == nums2[j]。

• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的
直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

2、解题思路

• 如果我们将数组看为一个字符串，那么这道题其实就是求两个数组的 LCS 问题：

直线不能相交，也就是说在数组 A 中找到一个与数组 B 相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，那么链接相同数字的直线就不会相交。

3、解题代码

public int maxUncrossedLines(int[] nums1, int[] nums2) {
    if (nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0) return 0;
    int len1 = nums1.length;
    int len2 = nums2.length;
    int[][] dp = new int[len1 + 1][len2 + 1];
    for (int i = 1;i <= len1;i++) {
        for (int j = 1;j <= len2;j++) {
            if (nums1[i - 1] == nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[len1][len2];
}

1.4、最大子序和

1、题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

• 示例一

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

2、解题思路

• 确定 dp 数组含义

其中 dp[i] 表示包括下标 i 之间的最大连续子序列和。

• 确定递推公式

对于 dp[i] ，有两个方向可以将其推导出来。

• dp[i - 1] + nums[i]

这表示将当前元素加入到以 i - 1 为下标的连续子序列和中，此时 dp[i - 1] 大于等于 0。

• nums[i]

这表示重新计算连续子序列和，以 i - 1 为结尾下标的连续子序列和的值小于 0 ，此时 dp[i - 1] + nums[i] 的值反倒小于 nums[i]。

• 初始化 dp 数组

由于 dp[i] 表示包括下标 i 之间的最大连续子序列和，所以对于 dp[0] ，我们可以将其初始化为 nums[0]。

3、解题代码

public int maxSubArray(int[] nums) {
    // base case 
    if (nums == null || nums.length == 0) return 0;
    // 使用一个变量来表示我们要返回的最大结果，初始化为 nums[0]
    int max = nums[0];
    // 创建一个长度为 nums.length 的 dp 数组
    int[] dp = new int[nums.length];
    // 初始化 dp 数组，dp[i] 表示以 i 下标为结尾的最大子序和的值，所以我们直接初始化 dp[0] 为 nums[0]
    dp[0] = nums[0];
    for (int i = 1;i < nums.length;i++) {
        // 进行选择
        //1 选择一，将 nums[i] 加入到以 i - 1 为结尾的子序列和中
        //2 选择二，直接将 nums[i] 看为一次新的开始
        dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
        // 更新最大结果
        max = Math.max(dp[i], max);
    }
    return max;
}

1.5、判断子序列

1、题目描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，”ace”是”abcde”的一个子序列，而”aec”不是）。

• 示例一

输入：s = "chm", t = "hialchemist"
输出：true

2、解题思路

方法一：使用双指针解决这道题。

• 初始化两个指针，其中 sub 指针指向 s 的第一个字符，main 指针指向 t 的第一个字符。

• 如果 sub 与 main 指向的字符相等，那么 sub 与 main 同时后移。

• 如果不相等，那么此时 sub 保持不动，而 main 后移。

方法二：使用动态规划求解这道题，我们可以求解出两个字符串的最长公共子序列长度 len ，然后判断 len 是否等于 s 的长度，所以问题又变为了求两个字符串最长公共子序列的问题。

• dp 数组的含义，其中， dp[i][j] 表示字符串 s 以 i - 1 下标为结尾的子串与字符串 t 以 j - 1 下标为结尾的子串，它们的最长公共子序列长度。

• 状态转移方程

1、如果 s.charAt(i - 1) == t.charAt(j - 1) ，那么 dp[i][j] = dp[i - 1][j - 1] + 1。

2、如果 s.charAt(i - 1) != t.charAt(j - 1) ，那么 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])。

• dp 数组的初始化，由于 dp[i][0] 、 dp[0][j] 无意义，所以初始化为 0。

方法三：使用动态规划解决这道题，我们以示例中所给的两个字符串进行打表。

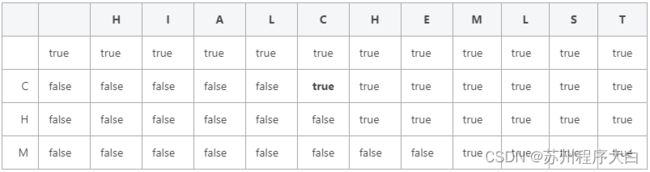
1、在上面的表格中，横向的行上分布着字符串 t ，而纵向的列上分布着字符串 s ，对于第一行，我们全将内容置为 true ，这表示当 s 为空字符串时，无论 t 为什么， s 都是 t 的子序列；对于第一列，我们将除（1，1）以外内容全部置为 false ，这表示当 t 为空字符串时，除了 s 为空串的情况外，s 都不是 t 的子串。

2、当s == "c" 且 t == "hialc"时，此时我们查看这个格子的左上角，发现这个格子的左上角也为 true ，这表示当 s 与 t 的最后一个字符相等时，此时我们只需要判断 s 去掉最后一个字符的子串 s[0, s.length() - 2]是不是 t 去掉最后一个字符的子串 t[0, t.length() - 2]的子序列即可，如果是，则结果为 true ，否则为 false。

// 假设 dp[i][j] 表示 s[0, i - 1] 是否为 t[0, j - 1] 的子序列
if (s.charAt(i - 1) == t.charAt(i - 1)) {
	dp[i][j] = dp[i - 1][j - 1];
}

如果有一个元素 dp[i][j] = true ，那么对于该行中该元素后的所有元素，应该全部为 true ，比如说 s = “c” 是 t = “abc” 的子序列，那么 s 就应该是 t = “abcd” 、 “abcde” 的子序列。

if (s.charAt(i - 1) != t.charAt(i - 1)) {
	dp[i][j] = dp[i][j - 1];
}

3、解题代码

双指针法

public boolean isSubsequence(String s, String t) {
    if (t.length() == 0 && s.length() != 0) return false;
    int sub = 0, main = 0;
    while (sub < s.length() && main < t.length()) {
        if (s.charAt(sub) == t.charAt(main)) {
            sub++;
        }
        main++;
    }
    return sub >= s.length();
}

动态规划一，解法二

public boolean isSubsequence(String s, String t) {
    if (t.length() == 0 && s.length() != 0) return false;
    int length1 = s.length(), length2 = t.length();
    int[][] dp = new int[length1 + 1][length2 + 1];
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            if (s.charAt(i - 1) == t.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[length1][length2] == s.length();
}

动态规划二，解法三

public boolean isSubsequence(String s, String t) {
    if (t.length() == 0 && s.length() != 0) return false;
    int length1 = s.length(), length2 = t.length();
    boolean[][] dp = new boolean[length1 + 1][length2 + 1];
    // base case ，由于这里行数是 s 长度，所以我们应该将第一列置为 true 
    for (int j = 0;j <= length2;j++) {
        dp[0][j] = true;
    }
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            // 如果 i - 1 与 j - 1 指针指向的字符相等，那么判断 s[0, i - 2] 是否为 t[0, j - 2] 的子串（取左上角的元素）
            if (s.charAt(i - 1) == t.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                // 否则直接取它左边的元素即可
                dp[i][j] = dp[i][j - 1];
            }
        }
    }
    return dp[length1][length2];
}

1.6、不同的子序列

1、题目描述

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE"是"ABCDE"的一个子序列，而"AEC"不是）。

示例一

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabb b it
ra b bbit
rab b bit

示例二

输入：s = “babgbag”, t = “bag”
输出：5
解释：
如下图所示, 有 5 种可以从 s 中得到 “bag” 的方案。
ba b g bag
ba bgba g
b abgb ag
ba b gb ag
babg bag

2、解题思路

使用动态规划求解这道题

• 定义 dp 数组的含义。

其中dp[i][j]表示字符串 s 中下标范围为[0, i - 1]的子串，它的子序列中出现字符串 t 中下标范围为 [0, j - 1] 的子串的个数。

• 确定状态转移方程：

1、当 s[i - 1] != t[j - 1] 时，此时我们只能让 s 字符串中下标为 [0, i - 2] 位置的子串与 t 字符串中下标为[0, j - 1]的子串进行匹配，因为此时s[i - 1]不能用来匹配，所以有 dp[i][j] = dp[i - 1][j]。

2、当 s[i - 1] == t[j - 1] 时，此时我们有两种选择：

• 使用s[i - 1] 来与 t[j - 1]进行匹配，这种情况下， dp[i][j] = dp[i - 1][j - 1]。

• 不使用s[i - 1] 来与 t[j - 1] 进行匹配，这种情况下，dp[i][j] = dp[i - 1][j]。

这里借用 LeetCode 题解中一位老哥的图进行理解：

• 初始化 dp 数组

1、当 j == 0时，此时 t 字符串所给的子串 y 为空串，那么对于 s 中的任意一个子串 x ，x 都可以包含 y ，故 dp[i][0] = 1。

2、当i == 0时，此时 s 字符串所给的子串 x 为空串，那么对于 t 中除空串外的任意一个字符串 y ，x 都不可能包含 y ，所以 dp[0][j] = 0（这里的 j >= 1）。

3、解题代码

public int numDistinct(String s, String t) {
    if (t.length() > s.length()) return 0;
    // 创建一个二维的 dp 数组，其中 dp[i][j] 表示 s 字符串中下标范围为 [0, i - 1] 的子串 a 中，含有 t 字符串中下标范围为 [0,j - 1] 的子串 b 的个数
    int length1 = s.length(), length2 = t.length();
    int[][] dp = new int[length1 + 1][length2 + 1];
    // 初始化 dp 数组，当 j == 0时，dp[0][j] = 1
    for (int i = 0;i <= length1;i++) {
        dp[i][0] = 1;
    }
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            if (s.charAt(i - 1) == t.charAt(j - 1)) {
                // 如果 s[i - 1] == t[j - 1]，那么此时我们有两种选择
                // 选择 1 ，让 s[i - 1] 与 t[j - 1] 进行匹配，此时得到的结果为 dp[i - 1][j - 1] 
                // 选择 2 ，让 s[i - 1] 不与 t[j - 1] 进行匹配，此时得到的结果为 dp[i - 1][j]
                // 需要将这两个结果综合起来
                dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
            } else {
                // 如果 s[i - 1] != t[j - 1]，那么此时 s[i - 2] 与 t[j - 1] 进行匹配，因为 s[i - 1] 不能匹配
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[length1][length2];
}

1.7、两个字符串的删除操作

1、题目描述

给定两个单词 word1 和 word2 ，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

示例一

输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea"，第二步将"eat"变为"ea"

2、解题思路

动态规划解法一

确定 dp 数组的含义，dp[i][j] 表示以 i - 1 为结尾的字符串word1 和以j - 1为结尾的字符串 word2，想要达到相等，所需要删除的元素的最少次数。

• 确定递推公式

当 word1[i - 1] == word2[j - 1] 时，此时我们称word1[i - 1] 和 word2[j - 1] 为公共字符，增加公共字符后不会使最少删除次数发生改变，比如 site与 hae 的最少删除次数和 sit与 ha 的最少删除次数一致，所以有：

if (word1[i - 1] == word2[j - 1]) {
	dp[i][j] = dp[i - 1][j - 1]
}

• 当 word1[i - 1] != word2[j - 1] 时，我们需要考虑三种情况

1、删除 word1[i - 1] ，此时最少操作数为 dp[i - 1][j] + 1，这里的 1 就是删除 word1[i - 1] 这次操作。

2、删除 word2[j - 1] ，此时最少操作数为 dp[i][j - 1] + 1。

3、同时删除 word1[i - 1] 和 word2[j - 1] ，此时最少操作数为 dp[i - 1][j - 1] + 2，其中 2 为删除word1[i - 1]和 word2[j - 1] 两次操作，从三者之间取最小值，就是这种情况下的最小删除次数。

• 初始化 dp 数组

1、当 j == 0 时， word2 为空串，此时最小删除数等于word1 的长度，即 dp[i][0] = i 。

2、同理，当 i == 0 时， word1 为空串，此时最小删除数等于 word2 的长度，即 dp[0][j] = j 。

动态规划解法二

由题意得 word1 与 word2 长度，分别记为len1 和 len2 ，然后使用动态规划求解 word1 与 word2 的最长公共子序列长度，记为 maxLength ，我们要求的结果为len1 + len2 - 2 * maxLength 。

3、解题代码

解法一代码

public int minDistance(String word1, String word2) {
    int length1 = word1.length(), length2 = word2.length();
    if (length1 == 0) return length2;
    if (length2 == 0) return length1;
    int[][] dp = new int[length1 + 1][length2 + 1];
    // 初始化 dp 
    // 当 j == 0 时，word1 和 word2 的最小删除数为 word1 子串的长度，即 i 
    for (int i = 0;i <= length1;i++) {
        dp[i][0] = i;
    }
    // 同理初始化 dp[0][j]
    for (int j = 0;j <= length2;j++) {
        dp[0][j] = j;
    }
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                // 此时 word1[i - 1] 与 word2[i - 2] 相等，所以它是公共字符
                // 当前两个子串的最小删除数与去掉公共字符的最小删除数相等
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                // 此时有三种情况进行考虑，分别是
                dp[i][j] = Math.min(
                    Math.min(
                        //1 删去 word1[i - 1]
                        dp[i - 1][j] + 1,
                        //2 删去 word2[j - 1]
                        dp[i][j - 1] + 1),
                    //3 同时删去 word1[i - 1] 和 word2[j - 1]
                    dp[i - 1][j - 1] + 2
                );
                // 我们需要取上面三种情况的最小值
            }
        }
    }
    return dp[length1][length2];
}

解法二

public int minDistance(String word1, String word2) {
    int length1 = word1.length(), length2 = word2.length();
    if (length1 == 0) return length2;
    if (length2 == 0) return length1;
    int[][] dp = new int[length1 + 1][length2 + 1];
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return length1 + length2 - 2 * dp[length1][length2];
}

1.8、编辑距离

1、题目描述

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1、插入一个字符。

2、删除一个字符。

3、替换一个字符。

示例一

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例二

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

2、解题思路

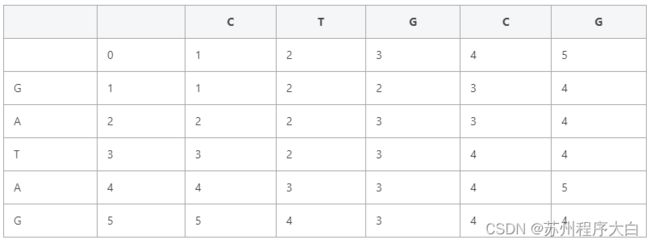
我们以一个例子，通过打表的方式来观察编辑次数与所给字符串的关系：

以 CTGCG 与 GATAG 为例：

1、当所给的字符串均为空串时，此时二者的编辑距离为 0。

2、当 s1 为空串，s2 不为空串时，此时二者之间的最短编辑距离为 s2.lengt()，反之亦然，所以我们可以将表格中的第一行第一列进行初始化。

3、当 s1 为 “G” 且 s2 为 “C” 时，二者的最小编辑距离为 1 ，此时只需要将 G 修改为 1 即可，我们根据 s1 与 s2 的情况填充表格。

• 定义 dp 数组的含义

其中 dp[i][j] 表示 word1 中下标范围为[0, i - 1]的子串 a 与word2中下标范围为 [0, j - 1]的子串 b ，它们二者之间的最短编辑距离。

• 状态转移方程

当 word1[i - 1] == word2[j - 1] 时，我们可以将这个相等的字符看为一个公共字符， word1[0. i - 1] 子串与 word2[0, j - 1] 子串的最短编辑距离与二者去掉公共字符后留下来的子串的最短编辑距离相等，比如说 hat 与 het最短编辑距离和 ha 与 he 的最短编辑距离相等。

dp[i][j] = dp[i - 1][j - 1]

• 当 word1[i - 1] != word2[j - 1] 时，此时我们有多个操作可供选择：

1、word1 删除一个元素，那么就是以下标 word1[0, i - 2] 与 word2[0, j - 1] 的最短编辑距离，再加上一个删除操作，此时得到的式子应该为 dp[i - 1][j] + 1。

2、word2 删除一个元素，那么就是以下标 word1[0, i - 1] 与 word2[0. j - 2]的最短编辑距离，再加上一个删除操作，此时得到的式子应该为 dp[i][j - 1] + 1。

3、替换元素，此时 word1 替换 word1[i - 1]，使其等于 word2[j - 1] ，此时我们又可以将 word1[i - 1]看为一个公共元素，只不过我们需要原来的基础上加上一次编辑，此时得到的式子为 dp[i - 1][j - 1] + 1。

4、对于添加操作来说， word1 添加一个字符，就相当于 word2 删除一个字符，比如说，当 word1 为 abce ，word2 为 abc 时，word1 删去 e与 word2 加上e 的结果都相同，所以我们只需要考虑删除的情况即可。

• 初始化 dp 数组

当两个字符串有一个为空串时，此时二者的最短编辑距离即为另外一个字符串的长度，我们假设 dp[i][j] 中，i 为 word1 字符串下标的变化情况，而 j 为 word2 字符串下标的变化情况，此时有：

1、当 j == 0 时，此时我们初始化 dp[i][0] = i。

2、当 i == 0 时，此时我们初始化 dp[0][j] = j。

3、解题代码

public int minDistance(String word1, String word2) {
    int length1 = word1.length(), length2 = word2.length();
    if (length1 == 0 && length2 == 0) return 0;
    if (length1 == 0 && length2 != 0) return length2;
    if (length2 == 0 && length1 != 0) return length1;
    // 创建一个 dp 数组
    int[][] dp = new int[length1 + 1][length2 + 1];
    // 初始化 dp 数组
    for (int i = 0;i <= length1;i++) {
        dp[i][0] = i;
    }
    for (int j = 0;j <= length2;j++) {
        dp[0][j] = j;
    }
    for (int i = 1;i <= length1;i++) {
        for (int j = 1;j <= length2;j++) {
            if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                // 对于公共字符，直接取去掉公共字符后的最短编辑距离即可
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                // 对于不是公共字符的情况，我们需要进行选择
                dp[i][j] = Math.min(
                    Math.min(
                        // 选择一：删除 word1[i - 1]
                        dp[i - 1][j] + 1,
                        // 选择二：删除 word2[j - 1]
                        dp[i][j - 1] + 1
                    ),
                    // 选择三：替换 word1[i - 1]
                    dp[i - 1][j - 1] + 1
                );
            }
        }
    }
    return dp[length1][length2];
}

1.9、最长回文子序列

1、题目描述

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例一

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例二

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

2、解题思路

• 确定 dp 数组的含义

其中 dp[i][j] 表示字符串 s 中下标范围为 [i ,j] 的子串 a 中最长回文子序列的长度。

• 确定递推公式

如果 s[i] == s[j] ，那么 dp[i][j] = dp[i + 1][j - 1] + 2。

如果 s[i] != s[j] ，那么此时 s[i] 与 s[j] 同时加入并不能增加 [i, j] 区间回文子序列的长度，那么我们分别加入 s[i] ，s[j] ，查看哪一个可以组成最长的最文子序列：

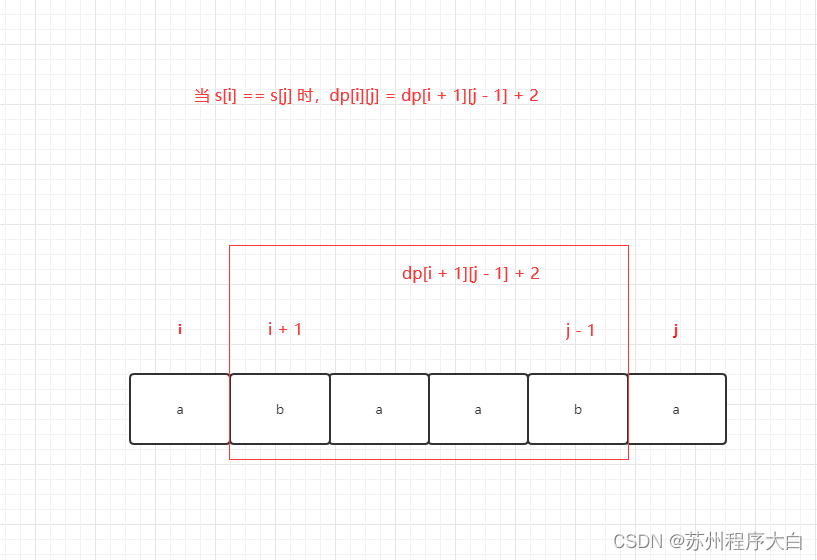
所以我们可以得出递推公式为：

if (s[i] == s[j]) {
	dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
	dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}

• 初始化 dp 数组

对于 dp[i][j] ，当 i == j 时，子串 s[i] 就 i是一个回文子序列，长度为 1，所以我们初始化 dp[i][i] = 1。

• 确定遍历顺序

根据递推公式，dp[i][j] 需要根据 dp[i + 1][j - 1] 、 dp[i + 1][j]和 dp[i][j - 1]退出，如果我们希望得出 dp[i][j] ，那么我们就先有当前行下一行的数据，所以对于外层行遍历，我们需要从尾到头进行遍历，而对于内层列遍历，我们需要从头到尾进行遍历。

3、解题代码

public int longestPalindromeSubseq(String s) {
    int len = s.length();
    if (len == 0) return 0;
    // 创建一个 dp 数组
    int[][] dp = new int[len][len];
    // 初始化 dp 数组
    for (int i = 0;i < len;i++) {
        dp[i][i] = 1;
    }
    for (int i = len - 1;i >= 0;i--) {
        for (int j = i + 1;j < len;j++) {
            if (s.charAt(i) == s.charAt(j)) {
                dp[i][j] = dp[i + 1][j - 1] + 2;
            } else {
                dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[0][len - 1];
}

2、让字符串成为回文串的最少插入次数

1、题目描述

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

示例一

输入：s = "zzazz"
输出：0
解释：字符串 "zzazz" 已经是回文串了，所以不需要做任何插入操作。

示例二

输入：s = "mbadm"
输出：2
解释：字符串可变为 "mbdadbm" 或者 "mdbabdm" 。

2、解题思路

• 确定 dp 数组的含义

其中 dp[i][j] 表示字符串 s 中下标范围为 [i,j] 的子串，要变为回文串所需要的最少插入次数。

• 确定状态转移方程

当 s[i] == s[j]时，此时对于子串s[i. j]而言，左右两边的字符不用修改，我们只需要求让下标范围为 [i + 1,j - 1]的子串变为回文串的最少插入次数即可，此时有 dp[i][j] = dp[i + 1][j - 1]。

比如说，对于字符串 abcda ，由于它左右两边的字符相等，所以我们只需要求出让 bcd 变为回文串的最少插入次数，即可求出让整个字符串变为回文串的最少插入次数。

1、当 s[i] != s[j] 时，此时我们需要选择最优的插入方案，即在下面的结果中选择最小值：

• 将 s[i] 插入 j - 1 的位置，同时将 s[j] 插入到i - 1 的位置，此时插入后的字符串中存在以下关系，即 s[i - 1] == s[j]且 s[i] == s[j - 1] ，比如说对于字符串 abcde ，我们将 s[i]插入到 e 的左边，将 s[j]插入到 a 的左边，字符串变为 eabcdae ，此时情况又转为了 s[i] == s[j] 的情况，我们只需要考虑 bcd 变为回文串所需要的最小插入次数即可，即 dp[i][j] = dp[i + 1][j - 1] + 2 ，这种做法可能不是最优解，比如说，对于字符串 aaax ，我们只需要在左边插入一个 x 就可以将其变为回文串。

• 我们先将s[i + 1,j]或者 s[i, j - 1] 变为回文串。假设将s[i + 1, j]变为回文串的代价 a 和将 s[i, j - 1]变为回文串的代价 b ，此时我们比较两个代价的大小，取代价小的那个子串进行修改，最后将结果 + 1 即得到将字符串 s[i,j] 变为回文串的最小插入次数，这种情况下，式子为 dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1；比如说对于字符串 aaax ，我们可以看出，将子串 aaa 变为回文串的代价较小，所以将 aaax 变为回文串的代价即为将 aaa 变为回文串的代价 + 1，即 1 。

2、所以，本题的状态转移方程如下：

if (s[i] == s[j]) {
	dp[i][j] = dp[i + 1][j - 1]
} else {
	dp[i][j] = Math.min(Math.min(dp[i + 1][j] + 1, dp[i][j - 1] + 1), dp[i + 1][j - 1] + 2);
}

• 初始化 dp 数组

当 i == j 时，此时子串中只有一个字符，所以该子串可以自成一个回文串，所以使其称为回文串的最少插入次数为 0 ，即 dp[i][i] == 0。

• 确定遍历顺序

这道题的遍历顺序与最长回文子序列一般，由于 dp[i][j] 依赖于下一行的数据，所以对于外层行遍历来说，我们需要从尾到头遍历，保证我们需要的结果（i + 1 行的数据）都是已经计算出来的。

3、解题代码

public int minInsertions(String s) {
    int len = s.length();
    if (len == 0 || len == 1) return 0;
    // 创建一个 dp 数组
    int[][] dp = new int[len][len];
    // 初始化 dp 数组
    for (int i = 0;i < len;i++) {
        dp[i][i] = 0;
    }
    // 外层循环从尾到头遍历
    for (int i = len - 1;i >= 0;i--) {
        // 内层循环从头到尾遍历，j 需要严格大于 i，因为 i == j 的情况我们在初始化时已经考虑过了
        for (int j = i + 1;j < len;j++) {
            if (s.charAt(i) == s.charAt(j)) {
                dp[i][j] = dp[i + 1][j - 1];
            } else {
                // 这种情况下，我们需要进行选择
                dp[i][j] = Math.min(
                    Math.min(
                        // 选择一：先将子串 s[i + 1,j] 变为回文串，然后在该基础上 + 1
                        dp[i + 1][j] + 1, 
                        // 选择二：先将子串 s[i, j - 1] 变为回文串，然后在基础上  +1
                        dp[i][j - 1] + 1
                    ),
                    dp[i + 1][j - 1] + 2
                );
            }
        }
    }
    return dp[0][len - 1];
}

2.1、俄罗斯套娃信封问题

1、题目描述

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi]，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

示例一

输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例二

输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1

2、解题思路

对于这道题来说，我们可以将所给数组的元素进行排序，先将这些信封根据宽度进行从小到大排序，对于宽度相等的信封，根据高度从大到小排序，比如说，对于示例一给的例子，在经过排序后，得到的顺序如下：

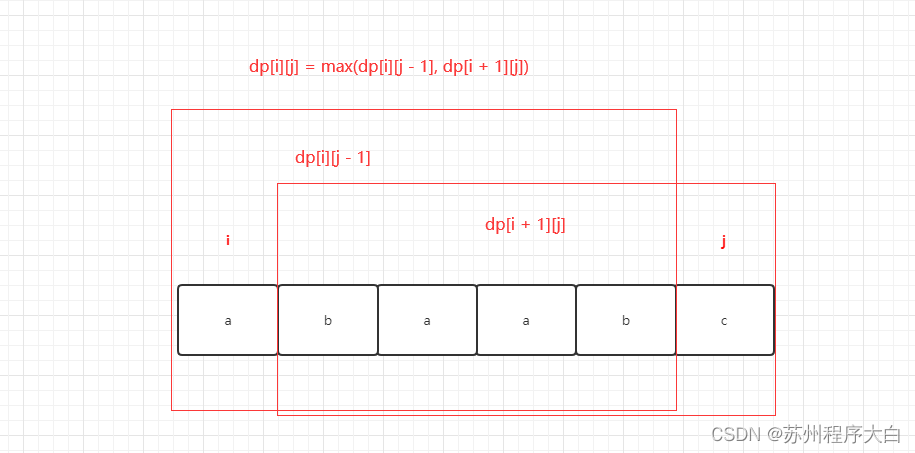
• 求 h 数组的最长递增子序列长度 maxLength，得到的结果就是本题的结果：

因为两个 w 相同的信封不能相互包含，所以在 w 相同时，我们将这些信封按照 h 从大到小排序，确保最多只有一个信封被选入到最长递增子序列中，这保证了最终的信封序列中不会出现多个 w 相同的信封。

3、解题代码

将传入的信封数组按照 w 从小到大进行排序，对于 w 相同的信封，根据 h 从大到小排序。

public int maxEnvelopes(int[][] envelopes) {
    if (envelopes.length == 0) return 0;
    // 对传入的信封数组进行排序，先根据 w 进行升序排序，对于 w 相等的元素，根据 h 进行降序排序
    Arrays.sort(envelopes, (envelopes1, envelopes2) -> envelopes1[0] == envelopes2[0] ? envelopes2[1] - envelopes1[1] : envelopes1[0] - envelopes2[0]);
    // 将所有信封的 h 看为一个数组，求这个数组的最长递增子序列长度
    // 创建一个 dp 数组
    int[] dp = new int[envelopes.length];
    // 初始化 dp 数组
    for (int i = 0;i < envelopes.length;i++) {
        dp[i] = 1;
    }
    // 使用一个变量来保存最长递增子序列长度，初始化为 1 
    int maxLength = 1;
    for (int i = 0;i < envelopes.length;i++) {
        for (int j = 0;j < i;j++) {
            if (envelopes[j][1] < envelopes[i][1]) {
                dp[i] = Math.max(dp[j] + 1, dp[i]);
            }
            maxLength = Math.max(dp[i], maxLength);
        }
    }
    return maxLength;
}

2.2、正则表达式匹配

1、题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持'.' 和 '*'的正则表达式匹配。

1、'.' 匹配任意单个字符。

2、'*' 匹配零个或多个前面的那一个元素。

所谓匹配，是要涵盖 整个 字符串 s 的，而不是部分字符串。

示例一

输入：s = "aa" p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例二

输入：s = "aa" p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

2、解题思路

对于 * ，我们需要将它与 * 号的前一个字符 x 看为一个整体，它表示可以匹配零个或者多个 x ，比如说 a* 可以匹配 0 个或者多个 a。

使用递归解决这道题：

• 编写一个递归函数 boolean process(char[] str, int si, char[] pattern, int pi) ，这个函数表示的含义为：字符串 str[si, str.length - 1] 能否被字符串 pattern[pi, pattern.length - 1]完全匹配。

• 编写 process 函数，我们需要保证传入的 pi 下标对应的字符不是 *。

1、base case 1，当 si == str.length 时，此时 str 表示的字符串为空串 “” ，这种情况下，如果 pi == length 或者 pattern 字符串剩下的子串可以与 “” 进行匹配，那么返回 true。

如何表示 pattern 字符串剩下的子串可以与 “” 进行匹配呢，即 pattern[pi] != “*“ && pattern[pi + 1] == “*“ && process(str, str.length, pattern, pi + 2)。

比如说，如果此时 pattern 剩下的字符串为 a*b*c* 时，就可以与空串进行匹配。

// 如果 si == str.length ，那么证明此时进行完全匹配的字符串 str 已经变为一个空串
if (si == str.length) {
    // 此时有两种情况可以返回 true
    // 第一种，此时 pattern 也为一个空串
    if (pi == pattern.length) {
        return true;
    }
    // 第二种，pattern[pi] 不为 * 且 pattern[pi + 1] 为 *
    // 同时 pattern [pi + 2,...] 可以与空串进行匹配
    if (pi + 1 < pattern.length && pattern[pi + 1] == '*') {
        return process(str, si, pattern, pi  +2);
    }
    // 如果无法满足上面的条件，那么直接返回 false
    return false;
}

1、 base case 2 ，当 pi == pattern.length 时，此时 pattern 已经为空串，那么此刻只有 s 为空串时，二者才能进行匹配。

2、当 si 与 pi 都没有到达最终位置时，此时又可以分为多种情况进行讨论。

• 如果 pi + 1 位置对应的字符不是 * ，那么有两种情况可以完全匹配成功，第一种就是 str[si] == pattern[pi] 且 后面的字符串可以完全匹配；第二种就是pattern[pi] == '.'且后面的字符串可以完全匹配。

• 如果 pi + 1 位置对应的字符是 * 且 str[si] != pattern[pi] ，那么此时只能让 pattern[pi]*变为 0 个 pattern[pi]，且需要满足 str[si] 及之后的字符串可以与 pattern[pi + 2]及之后的字符串完全匹配。

• 当 pi + 1 位置对应的字符是 * 且 str[si] == pattern[pi]时 ，此时就算str[si] == pattern[pi] ，pattern[pi] *也可能变为 0 个 pattern[pi]。

• 接下来我们就要判断 pattern[pi]*变为一个 pattern[pi]、多个pattern[pi]的情况了。

使用动态规划解决这道题

• 对于上面的 process 函数中，只有两个可变参数，即 si 与 pi ，当这两个参数确定后，得到的值（返回值）也就确定了，所以我们可以以 pi 为行， si 为列，以结果为值，将三者映射到一张二维表中。

• 确定 dp 数组的含义。

其中 dp[i][j] 表示字符串 str[i, ...] 与 pattern[j, ...] 是否可以进行完全匹配。

1、dp[i][j] == -1 ，表示 str[i, ...]与 pattern[j, ...] 的匹配结果没有计算过。

2、dp[i][j] == 0 ，表示 str[i, ...] 与 pattern[j, ...] 的匹配结果已经计算过了，且返回值为 false。

3、dp[i][j] == 1 ，表示 str[i, ...]与 pattern[j, ...] 的匹配结果已经计算过了，且返回值为 true。

• 初始化 dp 数组，根据上面我们提到的 dp 数组的含义，我们需要将 dp 数组中所有的元素都初始化为 -1。

• 在进行递归的过程中，我们需要将这张缓存表一起放入到递归函数中，然后对这张表进行存取。

在进行递归时，如果发现当前参数对应的值已经在缓存中出现（dp[i][j] != -1），那么不用计算，直接返回表中的值。

3、解题代码

递归

public boolean isMatch(String s, String p) {
    if (s == null || p == null) return false;
    char[] str = s.toCharArray();
    char[] pattern = p.toCharArray();
    return process(str, 0, pattern, 0);
}

/**
 * 判断 str[si, str.length - 1] 的子串能否被 pattern[pi, pattern.length - 1] 完全匹配
 */
public boolean process(char[] str, int si, char[] pattern, int pi) {
    // 如果 si == str.length ，那么证明此时进行完全匹配的字符串 str 已经变为一个空串
    if (si == str.length) {
        // 此时有两种情况可以返回 true
        // 第一种，此时 pattern 也为一个空串
        if (pi == pattern.length) {
            return true;
        }
        // 第二种，pattern[pi] 不为 * 且 pattern[pi + 1] 为 *
        // 同时 pattern [pi + 2,...] 可以与空串进行匹配
        if (pi + 1 < pattern.length && pattern[pi + 1] == '*') {
            return process(str, si, pattern, pi  +2);
        }
        // 如果无法满足上面的条件，那么直接返回 false
        return false;
    }
    // base case 2 ，当 pi == pattern.length 时，此时 pattern 已经为空串，那么此刻只有 s 为空串时，二者才能进行匹配
    if (pi == pattern.length) {
        return si == str.length;
    }
    // si 没有终止，pi 也没有终止
    //1 当 pi + 1 位置对应的字符不是 * 时
    if (pi + 1 >= pattern.length || pattern[pi + 1] != '*') {
        // 如果 si 对应的字符和 pi 对应的字符相等，或者 pi 对应的字符为 . ，且 si + 1 后的字符串可以与 pi + 1 后的字符串进行匹配，那么返回 true ，否则返回false
        return ((str[si] == pattern[pi]) || (pattern[pi] == '.')) && process(str, si + 1, pattern, pi + 1);
    }
    //2 当 pi + 1 位置对应的字符是 * 且 str[si] != pattern[pi] 时，此时只能让 pattern[pi]* 变为 0 个 pattern[pi]
    if (pattern[pi] != '.' && str[si] != pattern[pi]) {
        return process(str, si, pattern, pi + 2);
    }
    //3 当 pi + 1 位置对应的字符是 * 且 str[si] == pattern[pi] 时，
    // 此时就算 str[si] == pattern[pi] ，pattern[pi] * 也可能变为 0 个 pattern[pi]
    if (process(str, si, pattern, pi + 2)) {
        return true;
    }
    // 往下，我们判断 pattern[pi]* 变为一个或者多个 pattern[pi] 的情况
    while (si < str.length && (str[si] == pattern[pi] || pattern[pi] == '.')) {
        if (process(str, si + 1, pattern, pi + 2)) {
            return true;
        }
        si++;
    }
    // 否则直接返回 false
    return false;
}

动态规划

public boolean isMatch(String s, String p) {
    if (s == null || p == null) return false;
    char[] str = s.toCharArray();
    char[] pattern = p.toCharArray();
    int[][] dp = new int[str.length + 1][pattern.length + 1];
    for (int i = 0;i <= str.length;i++) {
        for (int j = 0;j <= pattern.length;j++) {
            dp[i][j] = -1;
        }
    }
    return process(str, 0, pattern, 0, dp);
}

/**
 * 判断 str[si, str.length - 1] 的子串能否被 pattern[pi, pattern.length - 1] 完全匹配
 */
public boolean process(char[] str, int si, char[] pattern, int pi, int[][] dp) {
    // 先查找缓存是否已经计算过，如果不等于 -1 ，那么证明计算过
    if (dp[si][pi] != -1) {
        return dp[si][pi] == 1;
    }
    // 下面，在我们进行返回前，需要将值存入缓存中然后再返回
    // 如果 si == str.length ，那么证明此时进行完全匹配的字符串 str 已经变为一个空串
    if (si == str.length) {
        // 此时有两种情况可以返回 true
        // 第一种，此时 pattern 也为一个空串
        if (pi == pattern.length) {
            dp[si][pi] = 1;
            return true;
        }
        // 第二种，pattern[pi] 不为 * 且 pattern[pi + 1] 为 *
        // 同时 pattern [pi + 2,...] 可以与空串进行匹配
        if (pi + 1 < pattern.length && pattern[pi + 1] == '*') {
            boolean result = process(str, si, pattern, pi  +2, dp);
            dp[si][pi] = result ? 1 : 0;
            return result;
        }
        // 如果无法满足上面的条件，那么直接返回 false
        dp[si][pi] = 0;
        return false;
    }
    // base case 2 ，当 pi == pattern.length 时，此时 pattern 已经为空串，那么此刻只有 s 为空串时，二者才能进行匹配
    if (pi == pattern.length) {
        boolean result = si == str.length;
        dp[si][pi] = result ? 1 : 0;
        return result;
    }
    // si 没有终止，pi 也没有终止
    //1 当 pi + 1 位置对应的字符不是 * 时
    if (pi + 1 >= pattern.length || pattern[pi + 1] != '*') {
        // 如果 si 对应的字符和 pi 对应的字符相等，或者 pi 对应的字符为 . ，且 si + 1 后的字符串可以与 pi + 1 后的字符串进行匹配，那么返回 true ，否则返回false
        boolean result = ((str[si] == pattern[pi]) || (pattern[pi] == '.')) && process(str, si + 1, pattern, pi + 1, dp);
        dp[si][pi] = result ? 1 : 0;
        return result;
    }
    //2 当 pi + 1 位置对应的字符是 * 且 str[si] != pattern[pi] 时，此时只能让 pattern[pi]* 变为 0 个 pattern[pi]
    if (pattern[pi] != '.' && str[si] != pattern[pi]) {
        boolean result = process(str, si, pattern, pi + 2, dp);
        dp[si][pi] = result ? 1 : 0;
        return result;
    }
    //3 当 pi + 1 位置对应的字符是 * 且 str[si] == pattern[pi] 时，
    // 此时就算 str[si] == pattern[pi] ，pattern[pi] * 也可能变为 0 个 pattern[pi]
    if (process(str, si, pattern, pi + 2, dp)) {
        dp[si][pi] = 1;
        return true;
    }
    // 往下，我们判断 pattern[pi]* 变为一个或者多个 pattern[pi] 的情况
    while (si < str.length && (str[si] == pattern[pi] || pattern[pi] == '.')) {
        if (process(str, si + 1, pattern, pi + 2, dp)) {
            dp[si][pi] = 1;
            return true;
        }
        si++;
    }
    // 否则直接返回 false
    dp[si][pi] = 0;
    return false;
}

点击直接资料领取

​ 这里有各种学习资料还有有有趣好玩的编程项目，更有难寻的各种资源。 ​ ​

❤️关注苏州程序大白公众号❤️