解密SVM系列（二）：SVM的理论基础

上节我们探讨了关于拉格朗日乘子和KKT条件，这为后面SVM求解奠定基础，本节希望通俗的细说一下原理部分。

一个简单的二分类问题如下图：

我们希望找到一个决策面使得两类分开，这个决策面一般表示就是 WTX+b=0 ,现在的问题是找到对应的W和b使得分割最好，知道logistic分类 机器学习之logistic回归与分类的可能知道，这里的问题和那里的一样，也是找权值。在那里，我们是根据每一个样本的输出值与目标值得误差不断的调整权值W和b来求得最终的解的。当然这种求解最优的方式只是其中的一种方式。那么SVM的求优方式是怎样的呢？

这里我们把问题反过来看，假设我们知道了结果，就是上面这样的分类线对应的权值W和b。那么我们会看到，在这两个类里面，是不是总能找到离这个线最近的点，向下面这样：

然后定义一下离这个线最近的点到这个分界面（线）的距离分别为d1,d2。那么SVM找最优权值的策略就是，先找到最边上的点，再找到这两个距离之和D，然后求解D的最大值，想想如果按照这个策略是不是可以实现最优分类，是的。好了还是假设找到了这样一个分界面 WTX+b=0 ,那么做离它最近的两类点且平行于分类面，如上面的虚线所示。好了再假设我们有这两个虚线，那么真实的分界面我们认为正好是这两个分界面的中间线，这样d1就等于d2了。因为真实的分界面为 WTX+b=0 ，那么就把两个虚线分别设置为 WTX+b=1 和 WTX+b=−1 可以看到虚线相对于真实面只是上下移动了1个单位距离，可能会说你怎么知道正好是一个距离？确实不知道，就假设上下是k个距离吧，那么假设上虚线现在为 WTX+b=k ，两边同时除k可以吧，这样上虚线还是可以变成 WT1X+b1=1 ,同理下虚线也可以这样，然后他们的中线就是 WT1X+b1=0 吧，可以看到从k到1，权值无非从w变化到w1,b变到b1,我在让w=w1,b=b1，不是又回到了起点吗，也就是说，这个中间无非是一个倍数关系。所以我们只需要先确定使得上下等于1的距离，再去找这一组权值，这一组权值会自动变化到一定倍数使得距离为1的。

好了再看看D=d1+d2怎么求吧，假设分界面 WTX+b=0 ，再假设X是两维的，那么分界面再细写出来就是： w1x1+w2x2+b=0 。上分界线： w1x1+w2x2+b=1 ，这是什么，两条一次函数（y=kx+b）的曲线是不是，那么初中就学过两直线的距离吧， d=|c2−c1|w21+w22−−−−−−−√=1||W||

这里W=(w1,w2)，是个向量，||W||为向量的距离，那么 ||W||2=WTW 。下界面同理。这样 D=d1+d2=2||W||=2WTW−−−−−√等效2WTW ,要使D最大，就要使分母最小，这样优化问题就变为 min(12WTW) ,乘一个系数0.5没影响，但是在后面却有用。

我们知道，如果一个一次函数分界面为 WTX+b=0 ，那么线上方的x可以使得 WTX+b>0 ,下方的x可以使得 WTX+b<0 吧，那么对于上界面以上的点就有 WTX+b>1 ，下界面以下的点就有 WTX+b<−1 。我们现在再假设上界面以上的点的分类标签为1，下界面以下的点的分类标签为-1。那么这两个不等式再分别乘以他们的标签会怎么样？是不是可以统一为 yi(WTxi+b)≥1 了（这也是为什么SVM在使用之前为什么要把两类标签设置为+1，-1，而不是0,1等等之类的了）。好了假设分界面一旦确定，是不是所有点都得满足这个关系。那么最终的带约束的优化问题转化为：

min12WTWs.t.yi(Wxi+b)≥1

把约束条件换成小于号的形式：

s.t.1−yi(Wxi+b)≤0

注意的是这可不是一个约束条件，而是对所有的每个样本xi都有一个这样的约束条件。
转换到这种形式以后是不是很像上节说到的KKT条件下的优化问题了，就是这个。但是有一个问题，我们说上节的KKT是在凸函数下使用的，那么这里的目标函数是不是呢？答案是的，想想 WT∗W ，函数乘出来应该很单一，不能有很多极点，当然也也可以数学证明是的。

好了那样的话就可以引入拉格朗日乘子法了，优化的目标变为：

L(w,b,α)=12wTw+α1h1(x)+...+αnhn(x)=12wTw−α1[y1(wx1+b)−1]−...−αn[yn(wxn+b)−1]=12wTw−∑i=1Nαiyi(wxi+b)+∑i=1Nαi

然后要求这个目标函数最优解，求导吧，

∂L∂w=w−∑i=1Nαiyixi=0⇒w=∑i=1Nαiyixi∂L∂b=−∑i=1Nαiyi=0⇒∑i=1Nαiyi=0

这两个公式非常重要，简直是核心公式。
求导得到这个应该很简单吧，那我问你为什么 WTW 对w求导是w呢？如果你知道，那么你很厉害了，反正开始我是一直没转过来。其实说起来也很简单，如果光去看看为什么求导以后，转置就没了，不太好想明白，设想一下假设现在是二维样本点，也就是最终的W=(w1,w2)，那么 WTW=w1∗w1+w2∗w2 那么对w1求导就是2w1,对w2就是2w2,这样写在一起就是对w求导得到(2w1,2w2)=2w了，然后乘前面一个1/2（这也就是为什么要加一个1/2），就变成w了。

好了得到上面的两个公式，再带回L中把去w和b消掉，你又可能发现，w确实可以消，因为有等式关系，那b怎么办？上述对b求导的结果竟然不含有b，上天在开玩笑吗？其实没有，虽然没有b，但是有那个求和为0呀，带进去你会惊人的发现，b还真的可以消掉，就是因为了那个等式。简单带下：

W(α)=L(w,b,α)=12(∑i=1Nαiyixi)T(∑j=1Nαjyjxj)−∑i=1Nαiyi((∑i=1Nαiyixi)xi+b)+∑i=1Nαi=12(∑i,j=1Nαiyiαjyjxi∗xj)−∑i,j=1Nαiyiαjyjxi∗xj+b∑i=1Nαiyi+∑i=1Nαi=−12(∑i,j=1Nαiyiαjyjxi∗xj)+∑i=1Nαi

那么求解最最开始的函数的最小值等价到这一步以后就是求解W的最大值了，因为使用了拉格朗日乘子法后，原问题就变为其对偶问题了，最小变成了最大，至于为什么，等到详细研究过对偶问题再来解释吧。不了解的，只需要知道求W的极值即可。
整理一下，经过这么一圈的转化，最终的问题为：

maxW(α)=−12(∑i,j=1Nαiyiαjyjxi∗xj)+∑i=1Nαis.t.αi≥0∑i=1Nαiyi=0

为什么有 αi≥0 ,这是上节说到的KKT条件的必须。至此问题来源部分到这。

细心的你肯可能会发现，上述所有的构造等等都是在数据完全线性可分，且分界面完全将两类分开，那么如果出现了下面这种情况：

正负两类的最远点没有明显的分解面，搞不好正类的最远点反而会跑到负类里面去了，负类最远点跑到正类里面去了，要是这样的话，你的分界面都找不到，因为你不可能找到将它们完全分开的分界面，那么这些点在实际情况是有的，就是一些离群点或者噪声点，因为这一些点导致整个系统用不了。当然如果不做任何处理确实用不了，但是我们处理一下就可以用了。SVM考虑到这种情况，所以在上下分界面上加入松弛变量 ϵi ,认为如果正类中有点到上界面的距离小于 ϵi ，那么认为他是正常的点，哪怕它在上界面稍微偏下一点的位置，同理下界面。还是以上面的情况，我们目测下的是理想的分解面应该是下面这种情况：

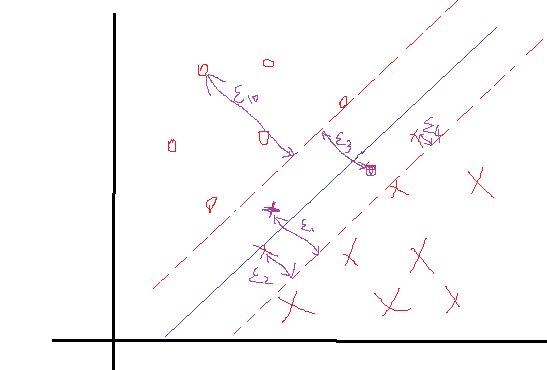
如果按照这种分会发现4个离群点，他们到自己对应分界面的距离表示如上，理论上讲，我们给每一个点都给一个自己的松弛变量 ϵi ，如果一个分界面求出来了，那么比较这个点到自己对应的界面（上、下界面）的距离是不是小于这个值，要是小于这个值，就认为这个界面分的可以，比如上面的 ϵ3 这个点，虽然看到明显偏离了正轨，但是计算发现它的距离d小于等于我们给的 ϵ3 ，那么我们说这个分界面可以接受。你可能会说那像上面的 ϵ10 ，距离那么远了，他肯定是大于预设给这个点的 ϵi 了对吧，确实是这样的，但是我们还发现什么？这个点是分对了的点呀，所以你管他大不大于预设值，反正不用调整分界面。需要调整分界面的情况是只有当类似 ϵ3 这样的点的距离大于了 ϵ3 的时候。

好了那么因为松弛变量的加入，导致每个点的约束条件就变化了点，像上界面以上的点，它满足的条件可能就是： WTxi+b≥1−ϵi,yi=1
而下界面可能就是： WTxi+b≤−1+ϵi,yi=−1
并且 ϵi≥0 。
统一在一起，整个问题就变成：

min12WTW+C∑i=1Nϵis.t.1+ϵi−yi(Wxi+b)≤0ϵi≥0

你发现目标函数里面多了一点东西，而加上这个是合理的，我们在优化的同时，也使得总的松弛变量之和最小。常数C决定了松弛变量之和的影响程度，如果越大，影响越严重，那么在优化的时候会更多的注重所有点到分界面的距离，优先保证这个和小。
好了将问题写在一起吧：

L(x,α,β)=12WTW−∑i=1Nαi(yi(Wxi+b)+ϵi−1)+C∑i=1Nϵi−∑i=1Nriϵi

然后对 w,b,ϵ 分别求导数：

∂L∂w=w−∑i=1Nαiyixi=0⇒w=∑i=1Nαiyixi∂L∂b=−∑i=1Nαiyi=0⇒∑i=1Nαiyi=0∂L∂ϵi=0⇒C−αi−ri=0

观察第三个式子，因为 ri≥0 ,所以 c−αi≥0⇒αi≤C ,结合 αi≥0 那么 0≤αi≤C ,把这三个导数结果带到目标函数中去消掉对应的w，b以及 ri ,你会惊人的发现，连 ϵi 也消掉了，并且目标函数和没有加松弛变量的一模一样：

W(α)=−12(∑i,j=1Nαiyiαjyjxi∗xj)+∑i=1Nαi

这么说，溜了一圈下来，无非多了个 αi≤C ,其他的什么也没有变，真好。那么统一一下，更一般的带松弛变量的优化函数以及约束条件就变为：

W(α)=−12(∑i,j=1Nαiyiαjyjxi∗xj)+∑i=1Nαis.t.0≤αi≤C∑i=1Nαiyi=0

剩下的问题是怎么去找这样一组最优解 αi 了。看过上节的可能会知道，在上节的最后那个实例中也是寻找 αi ，不过那里只有两个 αi ，而 αi 要么等于0，要么大于0，而 αi 大于0的时候，对应的另外一个因子就等于0。然后讨论这四种情况找到满足解。但是我们这里的 αi 可不止2个，想挨着讨论是不行的，且这里的KKT条件和上节的那个还不太一样。那么这里的KKT条件是什么呢？具体又要怎么解这样一堆 αi 的问题呢？请看下节的SMO算法求解SVM问题。