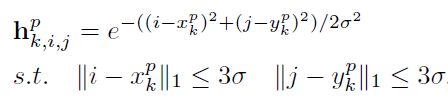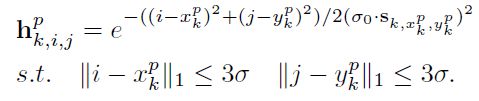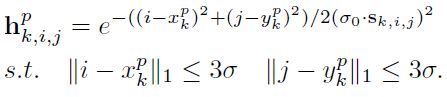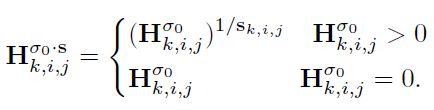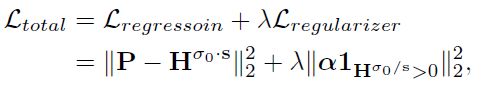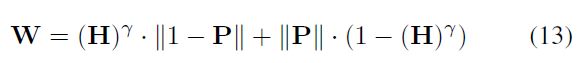【论文阅读笔记】Rethinking the Heatmap Regression for Bottom-up Human Pose Estimation
论文地址:https://arxiv.org/abs/2012.15175
代码地址:https://github.com/greatlog/SWAHR-HumanPose
论文总结
本文所针对的问题,是Bottom-up方法中的不同对象尺度会造成的问题。同一张图的不同尺度对象所对应的感受野不同,因此也应该有不同kernel size的高斯核heatmap。所以对于bottom-up方法,尺度适应的heatmap回归方法自适应每个keypoint的标准差,与此同时,提出自适应权重heatmap回归的损失函数以解决其产生的问题(前背景失衡问题)。
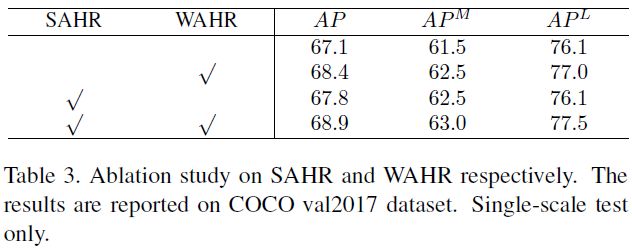
尺度自适应heatmap回归的名称为SAHR(scale-adaptive heatmap regression),权重自适应heatmap回归的名称为WAHR(weight-adaptive heatmap regression)。
如下图(b)和(c)所示,同一张图的不同对象应该有不同的高斯核,否则鼻子上的高斯核可能比脸还大。
论文简介
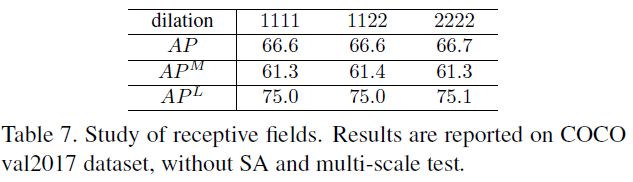
在实际应用中,不同的Keypoint都应用了相同标准差的高斯核,意味着不同的Keypoint有相同的heatmap监督。但这有两个不合理的原因:(1)Keypoint有不同的Scale,有不同的感知空间大小;(2)即使是人工标记,在像素级精度的关键点标注下,也会存在误差。使用高斯核可以给这个关键点提供模糊性。
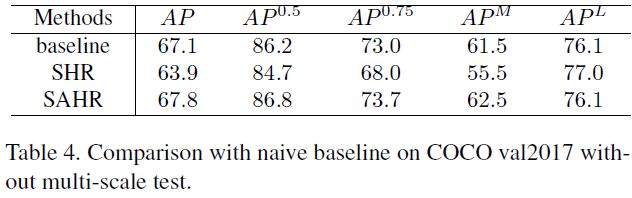
理论上,应该给每个关键点标注配套的标准差,但这是费时费力且难以定义定制的标准差。所以作者提出了SAHR,可以自适应地调整每个关键点的标准差。做法:(1)先用相同的标准差的高斯核在所有的关键点上;(2)加一个预测分支scale maps,其大小与heatmap相同;(3)对每个关键点,都修改原始的标准差为 σ ∗ s \sigma * s σ∗s。在某种程度上, s s s表示对应关键点的尺度。(4)最后,使用WAHR给不同难易样本添加权重,类似分类任务中的focal Loss。
对于常规的高斯核heatmap ground truth来说,如下图所示:
Scale-Adaptive Heatmap Regression
对于加了scale map的heatmap ground truth来说,变成了如下图所示公式:对应ground truth的关键点位置施加不同的scale 权重。
由于在高斯核范围内, S k , x k p , y k p ≈ S k , i , j S_{k,x^p_k,y^p_k}\approx S_{k,i,j} Sk,xkp,ykp≈Sk,i,j,所以上述公式变成如下的点乘格式,以方便实现:
实际上,在总体的Heatmap表示上,公式如下图所示:与原来的H的关系是一个指数关系,是一个element-wise的操作。
为了稳定训练,给scale map添加一个正则化项:
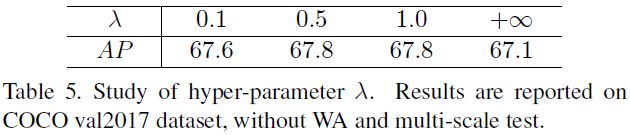
则损失函数变为:其中 λ = 1 \lambda=1 λ=1
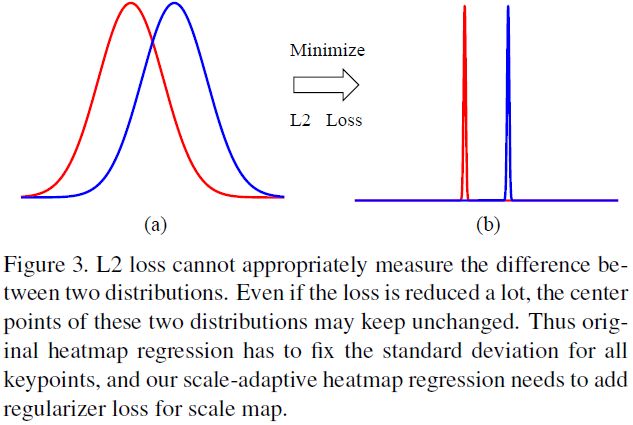
简单地使用L2 Loss最小化并不能得到正确地引导模型,如下图所示:
在SAHR上仍采用L2损失,但并没有保持高斯核标准差不变,而是采用正则项来帮助引导模型收敛到期望的方向。作者认为,SAHR结合了Heatmap和坐标回归的优点。Weight-Adaptive Heatmap Regression
Heatmap中大部分为0,可能会让模型更倾向于过拟合背景样本。最简单的方法是添加一个Weight tensor,但Heatmap回归是连续的,很难决定哪些是正样本,哪些是负样本。对于这个问题,提出了自适应的Heatmap回归方法(WAHR),其中W表现为如下所示:
其中 γ \gamma γ是控制位置的“软边界”的超参数,其决定的heatmap阈值 p p p为 1 − p γ = p γ 1-p^\gamma=p^\gamma 1−pγ=pγ,最后 p = 2 − 1 γ p=2^{-\frac1\gamma} p=2−γ1。实际上,作者采用 γ = 0.01 \gamma=0.01 γ=0.01。这里的 ∥ ⋅ ∥ 是 a b s 函 数 ; \| \cdot \|是abs函数; ∥⋅∥是abs函数;
当SAHR(scale-adaptive)和WAHR(weight-adaptive)一起使用时,称为SWAHR。
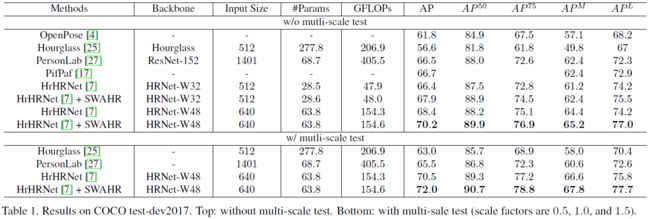
论文实验
使用的骨干网络为HrHRNet,是使用了deconv模块的HRNet。