目标检测(三):SSD
Single-Shot MultiBox Detector
-
- 0 简介
- 1 目标检测背景
- 2 网络结构
- 3 算法核心
-
- 3.1 使用多尺度特征图做检测
- 3.2 使用卷积预测器进行检测
- 3.3 default boxes尺度与宽高比的设置
-
- 3.3.1 default boxes 的尺度
- 3.3.2 default boxes 的宽高比
- 3.3.3 default boxes 的中心
- 4. 训练细节
-
- 4.1 default boxes 和 ground truth box的匹配策略
-
- 4.1.1 交并比
- 4.1.2 匹配方式
- 4.2 Hard negative mining
- 4.3 损失函数
-
- 4.3.1 位置损失
- 4.3.2 置信度损失
- 4.4 数据增强
-
- 4.4.1 放大操作
- 4.4.2 缩小操作
- 5. 实验结果及性能评估
-
- 5.1 PASCAL VOC 2007
-
- 5.1.1 实验细节
- 5.1.2 实验结果
- 5.1.3 错误模式分析
- 5.2 消融实验 (控制变量法)
- 5.3 其他数据集上的实验结果
- 6. 总结
-
- 6.1 优缺点
- 6.2 准确率提高的原因
- 6.2 速度提高的原因
- 7. 参考文章
想告诉师弟师妹们不要划水哇,因为后期开始准备毕设时都要补回来的~ /(ㄒoㄒ)/~~ 这篇文章参考了很多大佬的笔记,也有自己的一些理解,如果有不对的地方,恳请各路仙友批评指正。
还是共勉!
———————————————————————————————————————————
0 简介
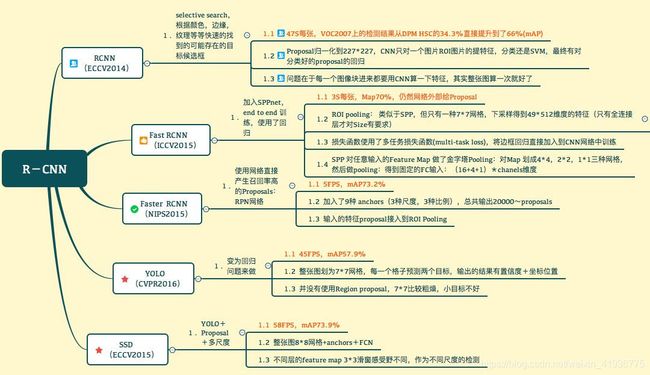
SSD 是 RCNN 系列中所实现性能比较高的一个模型,它在目标检测的准确性和速度上都远超之前。下面的图简单总结了基于 RCNN 的一系列模型。(图是之前在某个地方保存下来的,当时并没有保存链接,所以在这里先谢谢该图的作者~,如有冒犯真的不好意思)
SSD 由于优越的性能被广泛应用于医学图像领域,比如这篇关于日本胃癌的文章《Application of artificial intelligence using a convolutional neural
network for detecting gastric cancer in endoscopic images》,不得不感叹 SSD 在检测上的强大,不想阅读原文的小伙伴可以看下我粗略的笔记: AI医学:使用CNN进行内窥镜图像胃癌检测。
有关 SSD 的资料放在下面啦:
- Paper: Single-Shot MultiBox Detector
- Slide: SSD_ECCV2016_Slide
- Codes1: SSD Models based Caffe
- Codes2: SSD Models based Tensorflow
- Codes3: SSD Models based Pytorch
1 目标检测背景
传统的目标检测包括两个阶段:训练 + 预测
在 CNN 应用于目标检测之前,传统的目标检测方法可以分为两大类:
| 分类方法 | 举例 |
|---|---|
| 基于滑动窗口(sliding window) | DPM(Deformable Part Model) |
| 基于区域提议(region proposal) | Selective Search |
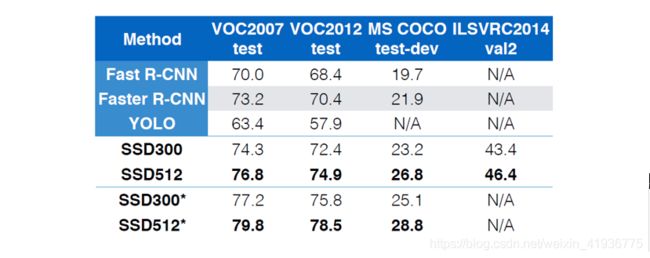
但 R-CNN 的出现,将通过选择性搜索得到的 region proposals 与 基于后分类(post-classification)的 CNN 结合在一起,为目标检测带来了巨大的改进(下图是 R-CNN 与一些传统检测方法的性能对比),自此基于 region proposal + classification 的方法成为目标检测中的主流方式。基于R-CNN,逐渐出现了许多能力更强大的模型(下表)。

| 模型 | 改进 |
|---|---|
| SPPNet,Fast R-CNN | 提高了后分类的质量和速度,但由于需要处理大量图像剪裁的分类,这类模型的计算量很大同时也非常耗时 |
| MultiBox,Faster R-CNN 等 | 改善了通过深层神经网络获取的region proposal的质量,提高了检测准确性,但因为需要训练两个互相依赖的网络而增加了复杂性 |
| OverFeat,YOLO , SSD 等 | 避免了利用其他网络生成 proposal,直接利用一个网络对多类别目标预测边界框和置信度,提升检测准确性的同时也提高了检测的速度,且避免了类似 Faster R-CNN 中的复杂性 |
根据以上性能不同的模型,region proposal + classification这种主流方式可以分为以下两类:
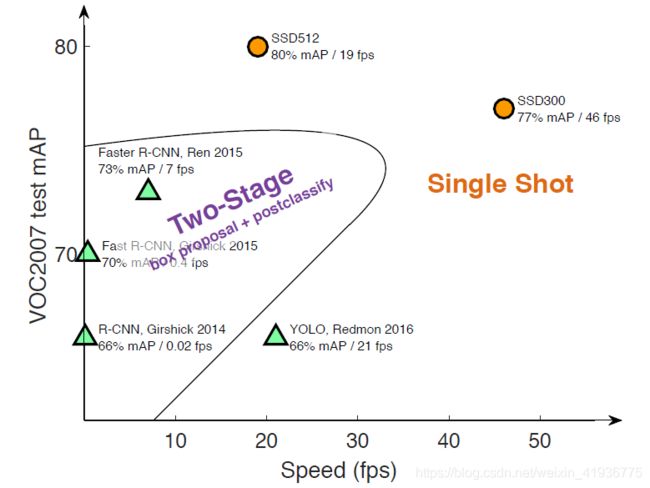
- Two-stage:如 R-CNN 系列模型,首先利用 Selective Search 或 RPN 产生一组稀疏的 region proposals,然后对这些 proposal 进行classification 和 bounding box regression 获取检测结果,这类模型的优点是准确性高,缺点是复杂度高;
- One-stage:即 Single-Shot,如OverFeat,YOLO,SSD 等模型,均匀地在不同的层上进行默认框(default box)抽样,利用 CNN 提取特征进行分类和回归,优点是速度快且准确性也高,缺点是通过抽样获得的正负样本比例不均衡导致训练困难,一定程度上影响检测准确性。
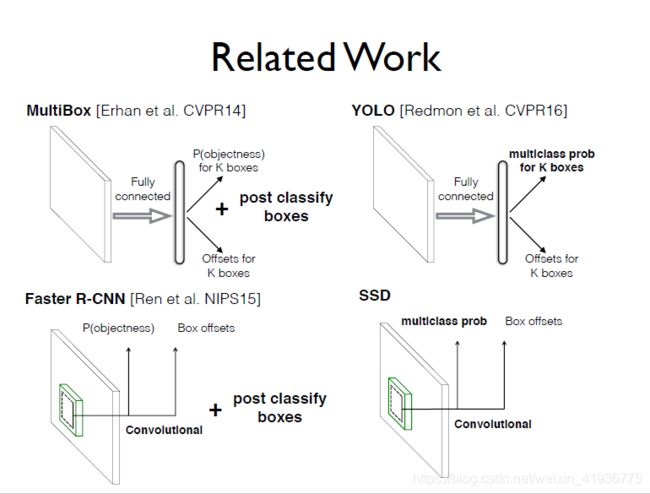
SSD 看它的名字就属于第二种了,但事实上 SSD 与上述的一些方法都或多或少的存在一些联系,作为这些模型的后继者可以说 SSD 做的很不错了(看下面的性能对比图,速度和准确性上 SSD 都拿到了一个新高):
- SSD 与 Faster R-CNN 中采用的 RPN 有些相似,因为 SSD 中用于预测的 default boxes 与 RPN 中的 anchor boxes 是类似的,但是 SSD 没有使用这些 boxes 来合并特征并利用另一个分类器产生预测结果,而是同时为每个 box 中的每个目标类别生成一个分数;
- 同时 SSD 与 OverFeat 也有相似之处,如果在来自最上层特征图的每个位置上仅使用一个 default box,则 SSD 将具有与 OverFeat 类似的体系结构;
- 与 SSD 最直接相关的是 YOLO 模型,如果使用整个最上层的特征图并添加一个用于预测的全连接层而不是使用卷积预测器,且不明确考虑多个宽高比,则可以近似地再现 YOLO。
default boxes 默认框,anchor boxes 锚框 以及 prior boxes 先验框,表达的都是同一个意思,在以下记录中遵循论文中使用的default boxes。
2 网络结构
SSD 包括两个模型:SSD300 & SSD512,区别在于两种模型的输入图像大小不同,前者是 300 × 300 300\times300 300×300,后者是 512 × 512 512\times512 512×512,除此以外模型的整体架构是一致的(也存在设置不同的部分,会在后面记录模型细节时提到)。论文中主要以 SSD300 为例做了讲解,以下记录中如果没有说明就默认 SSD 代表 SSD300。

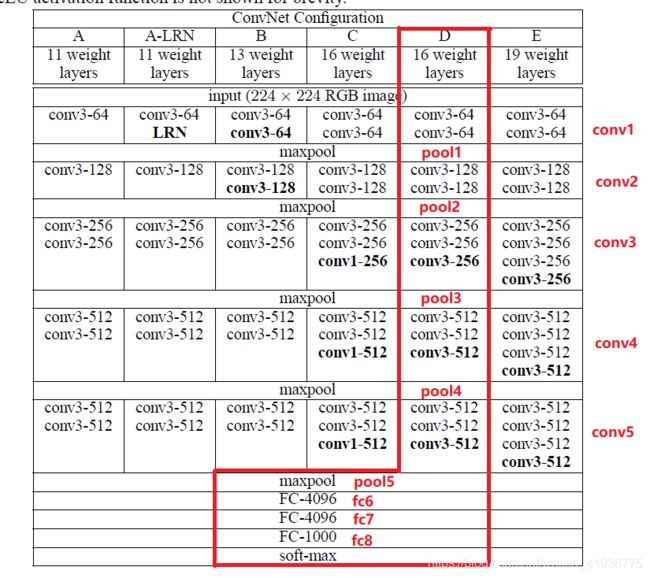
SSD 是以 VGG-16(即红框中的 D)为基础网络产生的,在使用 VGG-16 前,对其进行了以下修改:
- 分别将全连接层 fc6 和 fc7 更改为 3 × 3 3\times3 3×3 和 1 × 1 1\times1 1×1 的卷积层 conv6 和 conv7;
- 在 conv7 之后添加了额外的四个卷积层 conv8, conv9, conv10, conv11;
- 将池化层 pool5 由 2 × 2 s t r i d e = 2 2\times2\ stride=2 2×2 stride=2 更改为 3 × 3 s t r i d e = 1 3\times3\ stride=1 3×3 stride=1;
- 去掉了所有的 dropout 层和用于预测的全连接层 fc8。
- 添加了Atrous算法(Hole算法),以得到更稠密的得分图。
SSD 架构图红框中的部分即 VGG-16 保留下来的部分,其中conv4_3的特征图被抽取出来参与最终的预测,再加上修改后的卷积层,用于预测的特征图一共来自于六个层,其特征图大小分别为:
feature_layer = [conv4_3, conv7, conv8_2, conv9_2, conv10_2, conv11_2]
feature_shape = [(38,38), (19,19), (10,10), (5,5), (3,3), (1,1)]
通过下面的精简图,能够更清楚地理解 SSD 的流程:
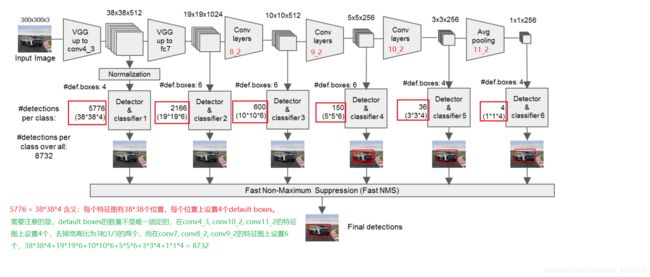
很容易看出,SSD 将 [conv4_3, conv7, conv8_2, conv9_2, conv10_2, conv11_2]的特征图 抽取出来用作回归和分类,这也是 SSD 的核心思想之一 —— 采用多尺度的特征图做检测 。通过上图我们可以大致得到 SSD 进行预测的步骤:
关于模型的细节部分,会在接下来的内容中记录。
3 算法核心
3.1 使用多尺度特征图做检测
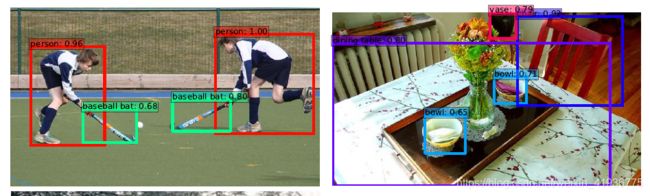
为什么要采用多尺度?从直觉上可以考虑一下对于复杂的目标检测问题,当一幅图像中含有大小不同的多种目标时,使用单一尺度的特征图是很难顾及到所有目标的。这是因为在一个特征图中,我们能够设置的default boxes 的尺度是固定的(后面的内容会介绍这里所说的尺度固定),所以一个特征图不可能兼顾到大目标和小目标,比如下面两幅图中的棒球棍、碗或花瓶,属于图像中比较小的目标,相对于人或餐桌这种较大目标而言,被检测到的概率是更小的 (这两幅图是 SSD512 在 COCO 的 test-dev 上所得的检测结果)。
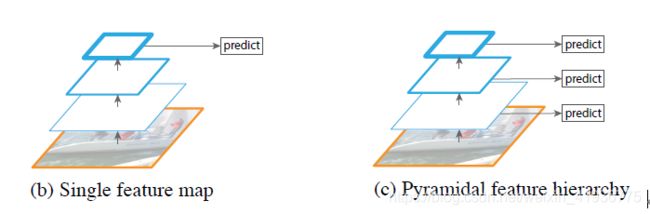
针对该问题,SSD 参考了 3. Feature Pyramid Networks for Object Detection 中的金字塔特征结构。SSD 出现之前的检测模型在预测时仅采用最后一层的特征图(如下面左边图所示);而 SSD 则采用了来自网络中不同层的特征图参与预测(如下面右边图所示),具体做法就是在基础网络 VGG-16 后添加了不同的卷积层,使得产生的特征图大小不同(实际上是逐层递减的),然后从中抽取了六个层的不同尺度的特征图,从而达到使用多尺度特征图的目的。
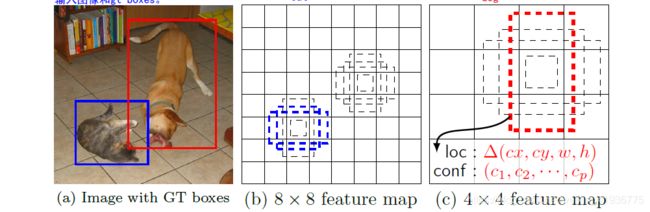
再从理论上验证下为啥要采用多尺度策略。先看下面的这副猫咪图,对一幅输入图像,SSD 抽取六个不同尺度的特征图(也就是白色虚框中的六种),相当于将图像划分成不同数量的小方格,然后我们看最右侧的图,显然猫咪所在的位置由 5 × 5 5\times5 5×5 特征图或 3 × 3 3\times3 3×3 特征图中的一个像素块来表示是比较准确的(SSD 实现的检测实际上是像素级的),也就是说对这样大小的猫咪而言,在检测中发挥主要作用的特征图是 5 × 5 5\times5 5×5 或 3 × 3 3\times3 3×3 。
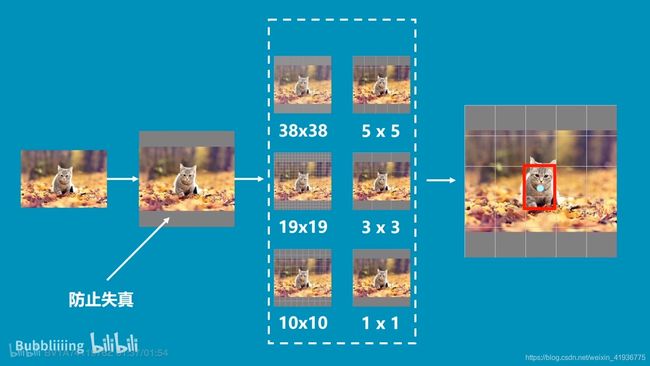
再来看另外一幅图,在这幅图中含有两个目标:猫咪和狗子,右侧给出了尺度分别为 8 × 8 8\times8 8×8 和 4 × 4 4\times4 4×4 的特征图,可以看到 8 × 8 8\times8 8×8 的特征图中存在两个 default boxes 与狗子匹配,但没有与猫咪匹配的 default box;相反,在 4 × 4 4\times4 4×4 的特征图中存在一个 default box 与猫咪匹配,但没有与狗子匹配的 default box,为什么会出现这种情况?事实上, 对于 8 × 8 8\times8 8×8 的特征图,尺寸大但感受野小,在每点处设置的 default boxes 尺度就比较小,从而可以检测较小的目标(也就是猫咪),而对于 4 × 4 4\times4 4×4 的特征图,尺寸小但感受野大,每点处设置的 default boxes 尺度较大,从而可以检测较大的目标(也就是狗子)。
这说明,当一幅图像中包含多个目标时,
- 较大的特征图可以检测到相对较小的目标,即低层预测小目标;
- 较小的特征图可以检测到相对较大的目标,即高层预测大目标。
因此采用多尺度的特征图,可以兼顾到图像中大小不同的目标,从而提高检测准确性。一开始没有理解为什么尺寸大的特征图反而能检测小的目标,看了b站某up主的视频讲解后突然就明白了,所以链接摆出来,大家快去围观他~ 4. Pytorch 搭建自己的SSD目标检测平台(Bubbliiiing 深度学习 教程)
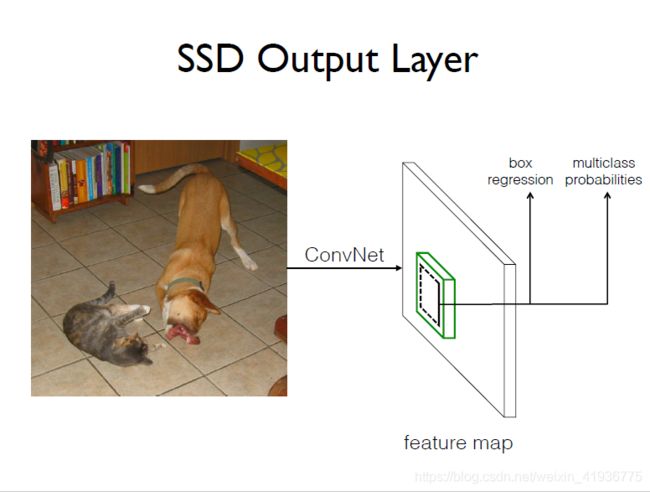
3.2 使用卷积预测器进行检测
简介中有提到 SSD 和 YOLO 是很相似的,不同点在于 YOLO 使用了全连接层提取检测结果,而 SSD 在基础网络后添加的是卷积层来提取特征并进行检测,近年来比较经典的几个基于深度学习的目标检测算法如 YOLOv3、FasterR-CNN中的RPN 以及 SSD 都采用了全卷积层做检测,那么为什么这些算法要将全连接层更改为全卷积层呢?
这篇文章 1. SSD原理解读-从入门到精通 中很详细的做了解释,有需要的盆友可以去看看这个,我就只记录一些个人理解。
- 一般采用全连接层的网络如 VGG、ResNet,后面会接 softmax 层来分类,既计算每一类别得分;
- 一般采用全连接层的网络,网络的最后两层都是全连接层(例如 VGG-16 中的 fc7 和 fc8),显然它们的作用是不相同的,fc7 用于提取特征,而 fc8 则是用于输出类别数(层的结点数即类别数,像 fc8,它的结点数 1000 就是类别数)。
之所以要提它们作用不同,就是因为全连接层本身带来的限制,一个全连接层所提取的特征是整张图的特征,所以对只包含一个目标的图像,使用全连接层提取特征是可以的,但如果一幅图有很多个目标,显然提取到的特征就无法准确的检测到所有目标。同时,由于全连接层的存在,网络的输入大小必须是固定的。因此,使用全连接层无法解决多目标检测问题。 这也就使得后期产生的算法将全连接层转换为卷积层进行特征提取和检测结果。
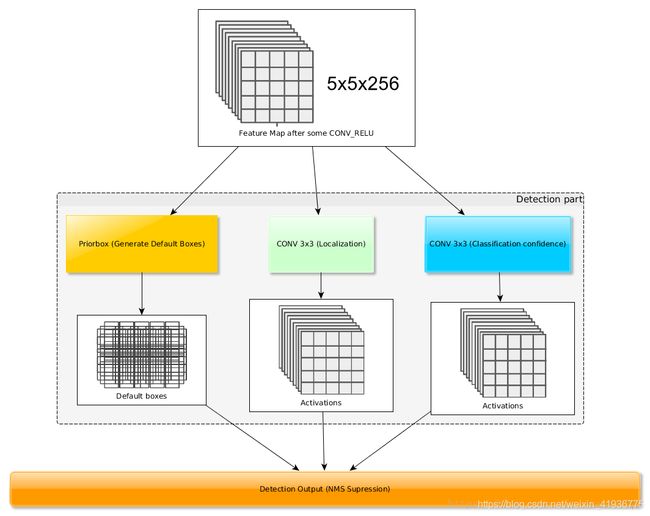
SSD 的做法是:对抽取出的六个层的特征图,假设在其上每一点处设置 k k k 个 default boxes,为了分类和获取最后的预测框,需要同时对每个 default box 计算其置信度 confidence(即类别得分) 和 边框偏移量 localization(即这四个参数: x , y , w , h x,y,w,h x,y,w,h),假设有 c c c 个类别,那么用于分类的卷积核个数为 c × k c\times{k} c×k;用于计算位置参数卷积核个数为 4 × k 4\times{k} 4×k,所以一共需要 ( c + 4 ) × k (c+4)\times{k} (c+4)×k 个卷积核。
3.3 default boxes尺度与宽高比的设置
在 1. SSD原理解读-从入门到精通 中看到过这样一句话(大意是这样,没太看懂原文中的实际相应区域,在原文的基础上改成了自己的理解):
因为目的是检测图像中的多个目标,而每个目标在图像中所对应的区域是不相同的,设置 default boxes 的作用就是将不同的目标和它们在图像中的区域联系在一起,又因为 default boxes 尺度和宽高比不同,这样每一层就可以对不同大小的目标响应,从而提取出每个 default box 对应区域中的目标的特征,这样就实现了同时提取多个目标的特征,进而达到实现检测多目标的目的。
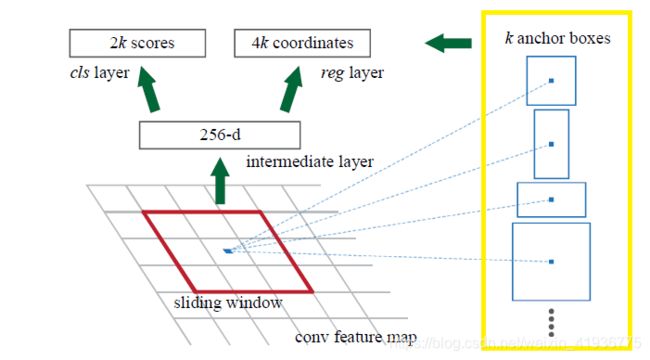
SSD 的 default boxes 与 Faster R-CNN中 anchor (下图黄色框内)的概念和作用是相同的,实际上就是在特征图的每一点处都设置的尺度和宽高比不同的边界框,最终的 predicted boxes 就是以这些 default boxes 为基准获取的。而YOLO在每个位置只选取正方形选框,但是真实目标的形状是多变的,YOLO 需要在训练过程中自适应目标的形状,所以 SSD 这种预设不同尺度和宽高比的default boxes的做法,在一定程度上可以减少训练难度。
3.3.1 default boxes 的尺度
假设使用的特征图个数为 m m m, s k s_k sk 表示第 k k k 个特征图中default boxes 的尺度,论文中给出了尺度的理论计算公式,说理论的原因是因为实验中的设置和该公式略有不同:
s k = s m i n + s m a x − s m i n m − 1 × ( k − 1 ) , k ∈ [ 1 , m ] s_k= s_{min}+\frac{s_{max}-s_{min}}{m-1}{\times}(k-1),\ k\in{[1,m]} sk=smin+m−1smax−smin×(k−1), k∈[1,m]
其中, s m a x = 0.9 , s m i n = 0.2 s_{max} = 0.9,\ s_{min}=0.2 smax=0.9, smin=0.2。多加一句,这篇记录都是针对 SSD300 的,在实验中:
- 将 SSD300 的 conv4_3 的特征图尺度设置为了 0.1;
- 在 SSD512 中新增了 conv12 并将 conv12_2 的特征图用于预测,设置了 s m i n = 0.15 s_{min} = 0.15 smin=0.15,将conv4_3 的特征图尺度设置为了 0.07。
有了公式我们就可以计算出每个特征图,前面已经说了抽取出来六个特征图参与预测,因为 conv4_3 的特征图尺度设置为了 0.1,所以用上述公式计算尺度的特征图个数为 5,默认的输入大小为 300 × 300 300\times300 300×300。
feature_layer = [conv4_3, conv7, conv8_2, conv9_2, conv10_2, conv11_2]
feature_shape = [(38,38), (19,19), (10,10), (5,5), (3,3), (1,1)]
| layer | s k s_k sk | min scale ( 0.7 4 ≈ 0.17 \frac{0.7}{4}\approx0.17 40.7≈0.17) | max scale |
|---|---|---|---|
| conv4_3 | 0.1 | 300 × 0.1 = 30 300\times0.1=30 300×0.1=30 | 60 60 60 |
| conv7 | 0.2 | 300 × 0.2 = 60 300\times0.2=60 300×0.2=60 | 111 111 111 |
| conv8_2 | 0.2 + 0.7 4 × 1 = 0.37 0.2+\frac{0.7}{4}\times1=0.37 0.2+40.7×1=0.37 | 300 × 0.37 = 111 300\times0.37=111 300×0.37=111 | 162 162 162 |
| conv9_2 | 0.2 + 0.7 4 × 2 = 0.54 0.2+\frac{0.7}{4}\times2=0.54 0.2+40.7×2=0.54 | 300 × 0.54 = 162 300\times0.54=162 300×0.54=162 | 213 213 213 |
| conv10_2 | 0.2 + 0.7 4 × 3 = 0.71 0.2+\frac{0.7}{4}\times3=0.71 0.2+40.7×3=0.71 | 300 × 0.71 = 213 300\times0.71=213 300×0.71=213 | 264 264 264 |
| conv11_2 | 0.2 + 0.7 4 × 4 = 0.88 0.2+\frac{0.7}{4}\times4=0.88 0.2+40.7×4=0.88 | 300 × 0.88 = 264 300\times0.88=264 300×0.88=264 | 315 315 315 |
关于最大尺度和最小尺度,论文中并没有提到这个,是看代码时发现的这个:
- 最大尺度和最小尺度就是我们用公式计算得到的该层和下一层的尺度;
- 然后这个 315 是怎么得来的,一开始有点懵,但是可以拿公式算出来, 315 = 300 × [ 0.2 + 0.7 4 × 5 ] 315 = 300\times[0.2+\frac{0.7}{4}\times5] 315=300×[0.2+40.7×5],感觉大概是为了避免边界框越界吧;
- 然后另一个问题是输入尺寸是 300 × 300 300\times300 300×300,最后为什么还能有的315 的尺寸,感觉应该是对输入图像做了预处理,就像 3.1 节中小猫咪的那个图,为了防止失真会在原图上下添加灰条,但我也不太懂,代码看的一知半解,还请各位大佬批评指正。
3.3.2 default boxes 的宽高比
对 default boxes 设置了不同的宽高比,记为 a r ∈ { 1 , 2 , 3 , 1 2 , 1 3 } a_r{\in}{\{1,2,3,\frac{1}{2}},\frac{1}{3}\} ar∈{1,2,3,21,31},对每个 default box,宽和高分别由以下公式来计算:
w k a = s k a r , h k a = s k a r w_k^a=s_k\sqrt{a_r},\ h_k^a=\frac{s_k}{\sqrt{a_r}} wka=skar, hka=arsk
除此之外,对 a r = 1 a_r=1 ar=1 时,再增加一个尺度为 s k ′ = s k s k + 1 {s_k'}=\sqrt{s_ks_{k+1}} sk′=sksk+1 的 default box,从而理论上来说,对特征图上的每个位置都能够设置6个不同的 default boxes。
但是在实验中并不是这样的:
- 对 conv4_3,conv10_2,conv11_2 的特征图,每点处仅设置宽高比为 { 1 , 2 , 1 2 , s k ′ } \{{1,2,\frac{1}{2}},s_k'\} {1,2,21,sk′}的 4 个default boxes;
- 对 conv7,conv8_2,conv9_2 的特征图,每点处设置上面提到的 6 个default boxes。
所以根据特征图尺度和 default boxes 的设置数量,可以计算出六个特征图总共产生的边界框数量:
( 38 × 38 + 3 × 3 + 1 × 1 ) × 4 + ( 19 × 19 + 10 × 10 + 5 × 5 ) × 6 = 8732 (38\times38+3\times3+1\times1)\times4+(19\times19+10\times10+5\times5)\times6=8732 (38×38+3×3+1×1)×4+(19×19+10×10+5×5)×6=8732
3.3.3 default boxes 的中心
对每个 default box,将其中心位置记为 ( i + 0.5 ∣ f k ∣ , j + 0.5 ∣ f k ∣ ) , i , j ∈ [ 0 , ∣ f k ∣ ] (\frac{i+0.5}{|f_k|},\frac{j+0.5}{|f_k|}),\ i,j{\in}[0,|f_k|] (∣fk∣i+0.5,∣fk∣j+0.5), i,j∈[0,∣fk∣],其中 ∣ f k ∣ |f_k| ∣fk∣ 是第 k k k 个方形特征图的大小。
4. 训练细节
训练 SSD 和使用 region proposals 的经典检测器的关键区别在于 是否需要将 ground truth 与一组特定的输出(也就是default boxes)相匹配 。事实上,在 SSD 之前的 YOLO、Faster R-CNN 中的 RPN、以及 MultiBox 中都需要进行该步骤,当这种匹配完成后,就可以计算损失然后进行反向传播来调整网络的参数,从而优化输出结果。论文中的这部分介绍了训练 SSD 所需的工作。
4.1 default boxes 和 ground truth box的匹配策略
刚刚也说了,需要首先确定图像中的 ground truth box与哪些 default boxes 相匹配,实际上就是拿这些 default boxes 来预测该 ground truth box代表的目标,然后相应地训练网络,所以,这一步真正的目的就是 构造正负样本,简单说就是,对任意一个 default box:
- 如果有与之匹配的 ground truth box,那它就是正样本;
- 反之如果没有和它匹配的 ground truth box,那它就是负样本。
需要注意的是,对于多目标图像,一个目标对应了一个 ground truth box,所以对每一个 ground truth box,我们都需要选出与之匹配的 default boxes。那么 SSD 是如何进行匹配的?以下就把ground truth 简记为 gt box。
4.1.1 交并比
首先要知道这个 jaccard overlap 的概念,俗称 交并比(IoU),用数学公式表达为:
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ = ∣ A ∩ B ∣ ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ J(A,B)=\frac{|A{\cap}B|}{|A{\cup}B|}=\frac{|A{\cap}B|}{|A|+|B|-|A{\cap}B|} J(A,B)=∣A∪B∣∣A∩B∣=∣A∣+∣B∣−∣A∩B∣∣A∩B∣
感觉学过集合就能理解这个概念,顾名思义就是两个集合的交和它们的并的比值。对图像而言, 或者说 default boxes 与 gt box,将其理解为像素的集合,容易理解点,然后再放个图叭。
- 黑色框表示一个 default box,
- 绿色框表示 gt box,
- 那么 IoU 就是白色框内模糊的区域。
4.1.2 匹配方式
- 对每一个 gt box,首先将与其 IoU 最大的 default box 相匹配,这么做是为了保证每个 gt box至少对应一个 default box,也就是保证每个目标至少可以被一个框检测到;
- 其次,对剩余没有配对的 default boxes,只要与任意一个 gt box存在 I o U > 0.5 IoU>0.5 IoU>0.5 的关系,就把它们匹配到一起;
- 经过上面两步,所有的 default boxes 被分为了两类,与 gt box匹配的即正样本,未与 gt box匹配的即负样本 (没能与任何一个 gt box匹配到一起,说明就只能和背景匹配,所以就变成负样本啦!)。

4.2 Hard negative mining
通过上述匹配方式,网络的学习可以被简化,对于有多个default boxes重叠的情况,网络可以获取多个预测值,而不再是选取其中重叠比最高的一个,但这也带来了另一问题—— 正负样本比例严重失衡。
尽管每个 gt box 都有相匹配的 default boxes (也就是正样本),但与所有的 default boxes 相比,gt box 是少数,这就导致剩余没有匹配的 default boxes 很多 (也就是负样本),即正样本偏少,负样本偏多,论文的 PPT 中给了一个大致的范围:
Unbalanced training: 1-30 TP, 8k-25k FP
这种严重的失衡无疑会影响网络的检测准确性,所以 SSD 采取了难负例挖掘的措施来实现正负样本的平衡。具体做法如下:
对 default boxes 的置信度损失进行降序排列,选取前 top-K 个,使得正负样本的比例保持在 1 : 3 1:3 1:3。置信度损失越大表明误差越大,这种负样本会更难预测 (也就是难负例);而对于置信度损失比较小的负样本,与背景之间的误差小,就会很容易检测到属于背景类,这样对训练网络而言是没什么太大帮助的,所以要选择损失置信度损失大的负样本。这一过程也就是难负例挖掘的思想。
4.3 损失函数
SSD 的损失函数与 6. Scalable Object Detection using Deep Neural Networks 的类似,不同点在于 SSD 的目的是含有处理多目标或者说是多类别的图像,该损失函数由 置信度损失(confidence loss) 和 位置损失(localization loss) 两部分组成:
L ( x , c , l , g ) = 1 N [ L c o n f ( x , c ) + α L l o c ( x , l , g ) ] L(x,c,l,g)=\frac{1}{N}[L_{conf}(x,c)+{\alpha}L_{loc}(x,l,g)] L(x,c,l,g)=N1[Lconf(x,c)+αLloc(x,l,g)]
其中:
- x x x 是一个示性函数, x i j p = { 1 , 0 } x_{ij}^p=\{1,0\} xijp={1,0}, 1 1 1 表示第 i i i 个 default box 和类别 p p p 的第 j j j 个 gt box 相匹配, 0 0 0 表示未匹配,通过匹配策略可以得到 ∑ i x i j p ≥ 1 {\sum_{i}{x_{ij}^p}}\geq1 ∑ixijp≥1,因为对每个 gt box 都至少有一个 default box 与之匹配;
- L c o n f , L l o c L_{conf},\ L_{loc} Lconf, Lloc 分别表示置信度损失和位置损失;
- N N N 表示正样本的数量,若 N = 0 N=0 N=0,则令 L ( x , c , l , g ) = 0 L(x,c,l,g)=0 L(x,c,l,g)=0;
- c , l , g c,\ l,\ g c, l, g 分别表示类别置信度预测值,predicted box 和 gt box的参数(即宽高和中心位置);
- 通过交叉验证得到的参数 α = 1 \alpha = 1 α=1。
4.3.1 位置损失
位置损失采用了 s m o o t h L 1 l o s s smooth_{L1}\ loss smoothL1 loss,该损失的计算要回归至 default bounding box (简记为 d d d) 的中心 ( c x , c y ) (cx,cy) (cx,cy) 及宽度( w w w)和高度( h h h)的偏移量。公式如下:
L l o c ( x , l , g ) = ∑ i ∈ P o s i t i v e N ∑ m ∈ { c x , c y , w , h } x i j k s m o o t h L 1 ( l i m − g ^ j m ) L_{loc}(x,l,g)=\sum_{i{\in}Positive}^{N}{\sum_{m{\in}\{cx,cy,w,h\}}}x_{ij}^ksmooth_{L1}(l_i^m-\hat{g}_j^{m}) Lloc(x,l,g)=i∈Positive∑Nm∈{cx,cy,w,h}∑xijksmoothL1(lim−g^jm)
根据 x i j p = { 1 , 0 } x_{ij}^p=\{1,0\} xijp={1,0} 这一定义,容易看出位置损失只针对正样本来计算。其中:
- l i m , g ^ j m l_i^m,\ \hat{g}_j^{m} lim, g^jm 分别表示第 i i i 个预测框 l l l 和调整的第 j j j 个 gt box 的中心、宽和高。
- 调整后的第 j j j 个 gt box 的中心、宽和高分别为:
- g ^ j c x = g j c x − d i c x d i w \hat{g}_j^{cx}=\frac{{g}_j^{cx}-d_i^{cx}}{d_i^{w}} g^jcx=diwgjcx−dicx
- g ^ j c y = g j c y − d i c y d i h \hat{g}_j^{cy}=\frac{{g}_j^{cy}-d_i^{cy}}{d_i^{h}} g^jcy=dihgjcy−dicy
- g ^ j w = l o g ( g j w d i w ) \hat{g}_j^{w}=log(\frac{{g}_j^{w}}{d_i^{w}}) g^jw=log(diwgjw)
- g ^ j h = l o g ( g j h d i h ) \hat{g}_j^{h}=log(\frac{{g}_j^{h}}{d_i^{h}}) g^jh=log(dihgjh)
4.3.2 置信度损失
置信度损失采用的是多个类别上的 s o f t m a x softmax softmax 损失:
L c o n f = − ∑ i ∈ P o s i t i v e N x i j p l o g ( c i p ^ ) − ∑ i ∈ N e g a t i v e l o g ( c i 0 ^ ) , c i p ^ = e x p ( c i p ) ∑ p e x p ( c i p ) L_{conf}=-\sum_{i{\in}Positive}^{N}x_{ij}^plog(\hat{c_i^p})-\sum_{i{\in}Negative}log(\hat{c_i^0}),\ \hat{c_i^p}=\frac{exp(c_i^p)}{\sum_p{exp(c_i^p)}} Lconf=−i∈Positive∑Nxijplog(cip^)−i∈Negative∑log(ci0^), cip^=∑pexp(cip)exp(cip)
其中, c i p ^ \hat{c_i^p} cip^ 表示的在 p p p 类别中,第 i i i 个default box 的置信度, p = 0 p=0 p=0 指的应该是背景。
4.4 数据增强
通过后面的实验可以得知数据增强是一个很重要的技巧,SSD 为使模型对各种输入目标的大小和形状有更高的鲁棒性,采取了多种数据增强的方法。
4.4.1 放大操作
首先是对每个训练图像均通过以下选项之一随机采样:
- 使用整个原始输入图像;
- 随机剪裁,选取一个 patch 使得该 patch 与目标的最小 IoU 为 { 0.1 , 0.3 , 0.5 , 0.7 , 0.9 } \{0.1,0.3,0.5,0.7,0.9\} {0.1,0.3,0.5,0.7,0.9} 或随机采样一个 patch,使得每个 patch 的大小为输入图像大小的 [ 0.1 , 1 ] [0.1,1] [0.1,1] 倍,宽高比在 [ 1 2 , 2 ] [\frac{1}{2},2] [21,2] 之间;
- 对于 gt box 的中心恰好位于 patch 中的情况,就保留 gt box 和 patch 的重叠部分。
其次对上述过程得到的样本进行亮度失真等操作,并将它们缩放到固定尺寸并以 0.5 的概率进行水平翻转,通过这种操作可以生成更多的尺度较大的目标。

4.4.2 缩小操作
在理论介绍数据增强时并没有提到缩小操作,这是在实验中添加的一个技巧,原因在于上述采样无法获得小目标,影响网络的准确性,所以…具体做法是:
创建大小是原图16倍的画布,并将原图放置其中,然后随机crop,进而生成更多尺度较小的目标。
5. 实验结果及性能评估
除了第二部分中介绍的对基础网络的设置外,实验中还使用了 Atrous algorithm,并使用随机梯度下降法(SGD)对所得模型进行微调,参数设置如下:
- 初始学习率为 l r = 1 0 − 3 lr = 10^{-3} lr=10−3
- 动量为 m o m e n t u m = 0.9 momentum=0.9 momentum=0.9
- 权重衰减为 w e i g h t d e c a y = 0.0005 weight decay=0.0005 weightdecay=0.0005
- 批次大小为 b a t c h s i z e = 32 batch\ size=32 batch size=32。
实际上每个数据集的学习率和衰减策略是不太相同的,在记录每个数据集上实验结果的时候会写出来。
5.1 PASCAL VOC 2007
5.1.1 实验细节
- 将基础网络 VGG 在 ILSVRC CLS-LOC dataset 上进行预训练,因此 conv7 之前的参数都无需进行初始化了,然后使用 Xavier 法对新增层的参数进行初始化。
- 将 conv4_3 特征图中 default boxes 的尺度设置为 0.1 0.1 0.1,剩余五层的尺度在 3.3.1 节中已经给出了;
- 对于每层特征图每个位置处设置的 default boxes 个数:
- 对于 conv4_3,conv10_2,conv11_2 的特征图,每点处仅设置宽高比为 { 1 , 2 , 1 2 , s k ′ } \{{1,2,\frac{1}{2}},s_k'\} {1,2,21,sk′} 的 4 个default boxes;
- 对于 conv7,conv8_2,conv9_2 的特征图,每点处设置宽高比为 { 1 , 2 , 3 , 1 2 , 1 3 , s k ′ } \{1,2,3,\frac{1}{2},\frac{1}{3},s_k'\} {1,2,3,21,31,sk′} 的 6 个default boxes。
- 由于conv4_3 的特征尺度不同于其他层,因此需要用 L2 Normalization 将特征图中每个位置处的特征范数缩放到 20 20 20;
- 关于迭代次数:
- 以 l r = 1 0 − 3 lr=10^{-3} lr=10−3 训练 40 k i t e r a t i o n s 40k\ iterations 40k iterations;
- 再分别以 l r = 1 0 − 4 、 1 0 − 5 lr=10^{-4}、10^{-5} lr=10−4、10−5 各训练 10 k i t e r a t i o n s 10k\ iterations 10k iterations。
5.1.2 实验结果



三张图分别展现了 SSD 在准确性和速度上相比其他模型的提升:
- 图一展现了相比Faster R-CNN,SSD300 在输入图像分辨率降低的情况下,尽管准确率提升幅度不大,但速度提高了 6.6 倍;
- 图二展现了 SSD512 与 YOLO 相比,尽管速度低了一点点点点点,但准确率提升了 10%,这显然要归功于 SSD 的 default boxes 密集采样了;
- 图三展现了 SSD 自身在 batch size 增大的情况下,速度反而得到了提升。
5.1.3 错误模式分析
SSD 使用了 detection analysis tool 分析模型的主要出错点。下图是 SSD512 在VOC 2007测试集上的部分检测数据。其中:
| 类型 | 含义 |
|---|---|
| Cor | 检测到的正确结果,即 TP |
| Loc | 因定位不良造成的假正例(FP) |
| Sim | 因与相似类别混淆造成的假正例(FP) |
| Oth | 因与其他类别混淆造成的假正例(FP) |
| BG | 因与背景混淆造成的假正例(FP) |
- 第一行的三幅图展现了召回率随检测数量的变化曲线,根据召回率的定义 R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP 和 图中大片空白的区域(也就是Cor),说明正确检测的结果是大多数,也就是SSD 能以较高的质量检测大部分的类别。同时可以看出在 I o U = 0.1 IoU=0.1 IoU=0.1 的弱标准下,召回率反而更高,这进一步表明了 SSD 的分类性能棒!!!
- 第二行展现了四种不同原因导致的假正例各自所占的比例。其中红色区域(即 Sim)比较大,这是因为 SSD 在类别之间是共享位置信息的,所以对相似类别的检测错误较多;其次是蓝色区域(即 Loc),虽然图中看起来也很大,但相比于 R-CNN,该类型的假正例要少得多,这表明 SSD 对目标的定位更好,事实上原因在于 SSD 直接使用回归来学习目标的形状(边界框)并进行分类。
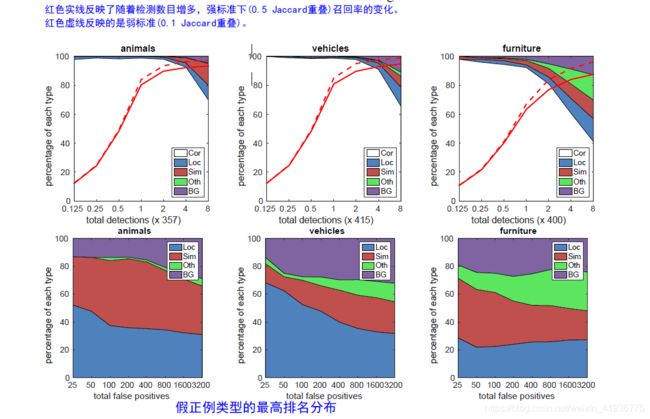
其次 SSD 对 bounding box 的大小很敏感,在小目标上的表现比更大目标上的表现要差得多,这是因为小目标在网络顶层可能甚至不存在任何信息,自然就难以检测到。论文中提到了可以通过增大输入的大小来改善检测小目标。但 SSD 对 不同的宽高比具有鲁棒性,这是因为在特征图的每点处都采用了不同宽高比的 default boxes。
5.2 消融实验 (控制变量法)
这部分通过实验证明了 SSD 中一些策略的必要性,是准确性和速度相比先前模型得以提升的必备条件。

- 数据增强很重要。
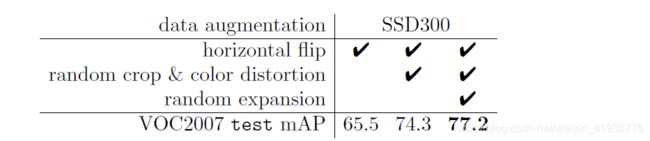
从上图可以看出,没有数据增强时的 mAP 只有 65.5 % 65.5\% 65.5% ,比加入数据增强后的 mAP 低了 $8.8%。再看下图,随着随机裁剪和颜色失真以及随即放大的不断加入,mAP 是逐渐提升的,这足以说明广泛的采样策略非常重要!!! - default boxes的形状多样化很重要。
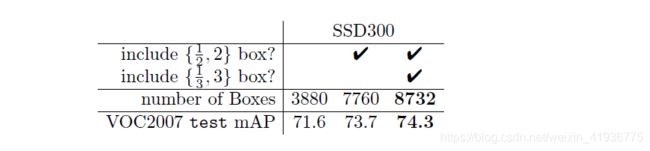
之前也提到过,理论上在特征图的每个位置处会设置六个宽高比不同的 default boxes,但在某些层去掉了最大和最小的两个尺度,仅使用四种宽高比。消融实验对比了使用不同宽高比情况下的 mAP,可以看出 SSD 对 default boxes 的密集采样策略是非常重要的,因为所设置的宽高比越多,越能够包含大小不同的各种目标。比如 { 3 , 1 3 } \{3,\frac{1}{3}\} {3,31} 代表了更小和更大的目标,当去掉这两种宽高比时,大目标和小目标就很难检测到了,自然 mAP 会降低。 - Atrous算法能够提升速度。
尽管 Atrous 算法只增加了 0.1 % 0.1\% 0.1% 的准确率,但它真实的作用是在提升检测速度上。 - 多尺度的特征图是必要的。

在该实验中,由于逐层删除会导致 default boxes 数量减少,为保证能与原始模型进行公平的对比,每移除一层时,会调整 tilling 以保证 default boxes 的总数与原始 8732 类似。当删除层并在剩余层增加 default box 时,有很多框会出现在图像边界上,此时选择忽略这些框。
从上图可以看出使用粗糙的特征图(eg:conv10_2,conv11_2)会降低性能,出现这种情况可能是由于裁剪后没有足够大的 box 覆盖大目标;当主要使用比较精细的特征图时,性能会恢复,这是因为即使修剪后也有足够大的 box 覆盖大目标;只使用 conv7 时从 74.3 % 74.3\% 74.3% 减少到 62.4 % 62.4\% 62.4%,性能极差,说明将不同尺度的 default boxes 分布到不同层至关重要。
5.3 其他数据集上的实验结果
6. 总结
总而言之,SSD 牛x。
6.1 优缺点
- 优点:
- 准确率上超越了 Faster R-CNN(针对稀疏场景的大目标而言);
- 运行速度上超过了YOLO。
- 缺点:
- 对小目标的检测效果一般,可能是因为小目标在高层没有足够的信息;
- 需要人工设置 default boxes 的初始尺度和宽高比;
- 同时网络中 default boxes 的基础大小和形状不能直接通过学习获得,但每一层 feature使用的default box大小和形状恰好都不一样,导致调试过程非常依赖经验。
6.2 准确率提高的原因
- 使用全卷积预测器;
- 使用多尺度的特征图;
- 设置了多种宽高比不同的 default boxes;
- 使用广泛的数据增强策略;
- 难负例挖掘。
6.2 速度提高的原因
- SSD 是一个 One-Stage 网络,只需要一个阶段就可以提取特征并分类以输出结果;
- 与全连接层相比,卷积层的参数更少,计算速度自然更快,而 SSD 是一个全卷积预测器;
- 使用了 Atrous 算法,该算法能够提速20%;
最后的最后,通过阅读 SSD 这篇文章明白了一个道理,只看理论不读代码是无法从本质上理解算法思想的,所以下一步就是深入的学习下 SSD 代码了。
7. 参考文章
- SSD原理解读-从入门到精通
- 目标检测算法——SSD详解
- Feature Pyramid Networks for Object Detection
- Pytorch 搭建自己的SSD目标检测平台(Bubbliiiing 深度学习 教程)
- SSD算法详解
- Scalable Object Detection using Deep Neural Networks
- code----Caffe实现
- code----Tensorflow实现
- code----Pytorch实现