GEO数据库学习三(了解表达矩阵)

上一节已经成功进行了id转换，这一节主要是了解表达矩阵，通过绘图等参数判断表达矩阵是否正确。首先需要根据上一节过滤的探针，我们需要把exprSet表达矩阵的行名(探针id)换成基因名，处理完之后表达矩阵的处理就全部完成了。

1.把exprSet表达矩阵的行名(探针id)换成基因名

#查看现在的表达矩阵信息
> dim(exprSet)
[1] 18851     6

#将ids表里的行匹配到exprSet里
> ids=ids[match(rownames(exprSet),ids$probe_id),]
> dim(ids)
[1] 18851     2
> head(ids)
  probe_id     symbol
2  7896754 SEPTIN7P13
3  7896759  LINC01128
4  7896761     SAMD11
5  7896779     KLHL17
6  7896798    PLEKHN1
7  7896817      ISG15

#现在exprSet和ids的探针id一一对应 则直接将ids的symbol赋值给exprSet的行名
> rownames(exprSet)=ids$symbol
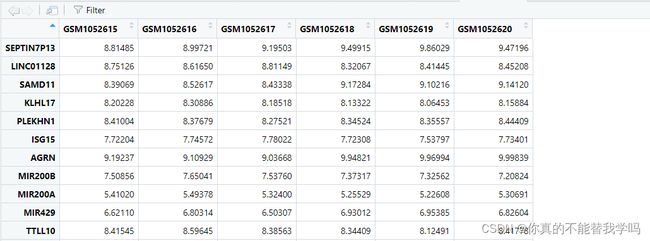
head(exprSet)
           GSM1052615 GSM1052616 GSM1052617 GSM1052618 GSM1052619 GSM1052620
SEPTIN7P13    8.81485    8.99721    9.19503    9.49915    9.86029    9.47196
LINC01128     8.75126    8.61650    8.81149    8.32067    8.41445    8.45208
SAMD11        8.39069    8.52617    8.43338    9.17284    9.10216    9.14120
KLHL17        8.20228    8.30886    8.18518    8.13322    8.06453    8.15884
PLEKHN1       8.41004    8.37679    8.27521    8.34524    8.35557    8.44409
ISG15         7.72204    7.74572    7.78022    7.72308    7.53797    7.73401

2.查看内参情况

可以查看内参情况，即一些管家基因的表达情况，比如GAPDH：

#查看内参情况 GAPDH
> exprSet[rownames(exprSet)=="GAPDH",]
GSM1052615 GSM1052616 GSM1052617 GSM1052618 GSM1052619 
   14.3187    14.3622    14.3638    14.4085    14.3569 
GSM1052620 
   14.3229 
#查看内参情况 GAPDH
> exprSet[rownames(exprSet)=="GAPDH",]
GSM1052615 GSM1052616 GSM1052617 GSM1052618 GSM1052619 GSM1052620 
   14.3187    14.3622    14.3638    14.4085    14.3569    14.3229 
#画一个boxplot查看这个值是高还是低
> boxplot(exprSet)

由图可以知道，六个样本每个探针表达量基本都是8，则14已经很高了，一般管家基因的表达水平要高于平均水平。

3.查看表达矩阵分布图

> library(ggplot2)
> library(reshape2)

#将表达矩阵转化成长list 拆分得到数据框 第一列基因名 第二列样品名 第三列value
#melt拆分数据
> exprSet_L=melt(exprSet)
> colnames(exprSet_L)=c('group','sample','value')
#6个样品 分别是对照和药物处理组 每一个都有3个重复 可以根据GEO网页显示的具体信息来命名 这里只区分对照和处理
> group_list=c(rep('control',3),rep('vemurafenib',3))
> #把长列表的表达矩阵里group一列命名为具体的样品名
> exprSet_L$group=rep(group_list,each=nrow(exprSet))
> head(exprSet_L)
    group     sample   value
1 control GSM1052615 8.81485
2 control GSM1052615 8.75126
3 control GSM1052615 8.39069
4 control GSM1052615 8.20228
5 control GSM1052615 8.41004
6 control GSM1052615 7.72204

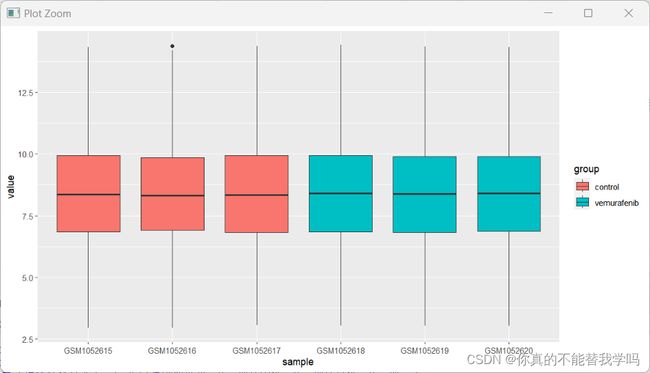
> p=ggplot(exprSet_L,aes(x=sample,y=value,fill=group))+geom_boxplot()
> print(p)

exprSet：

exprSet_L：

由图可知：样品中间的线基本在一条直线上，则可以一起进行比较，如果相差很多，则说明不是同一类东西，或者存在批次效应。

4.查看离群值

#查看离群值
ggplot(exprSet_L,aes(value,col=group))+geom_density()+facet_wrap(~sample,nrow = 4)

5.hclust图

hclust()层次聚类函数，聚类就是每一次把两类聚合成新的一类，知道所有的类聚成一个单类为止。
算法如下：

1. 定义每个观测(行或单元)为一类
2. 计算每类和其他各类的距离
3. 把距离最短的两类合并成一类 这样类就减少一个
4. 重复步骤2 3 知道包含所有观测值的类合并成单个的类为止

使用格式：hclust(d,method=)，d是通过dist()函数产生的距离矩阵，方法包括：“single” “complete” “average” “centroid"和"ward”。

hc=hclust(dist(t(exprSet)))
plot(hc)

根据hcluts图可以判断数据是否有问题，正常来说对照在一组，处理在一组，但由于本次画图的样品名还是GSM开头，为了更方便可以把表达矩阵的样品名称修改一下：

#修改表达矩阵样品名称
#group_list:"control" "control" "control" "vemurafenib" "vemurafenib" "vemurafenib"
> colnames(exprSet)=paste(group_list,1:3,sep='')
> colnames(exprSet)
[1] "control1"     "control2"     "control3"     "vemurafenib1" "vemurafenib2" "vemurafenib3"
> hc=hclust(dist(t(exprSet)))
> plot(hc)

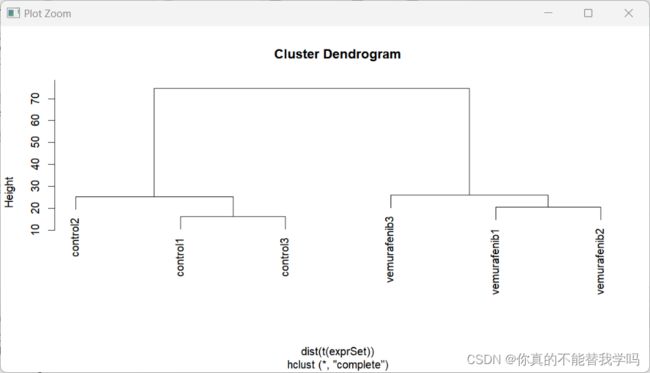
此时可以很清楚的看到对照和样品在不同的分组，说明表达矩阵没有问题。

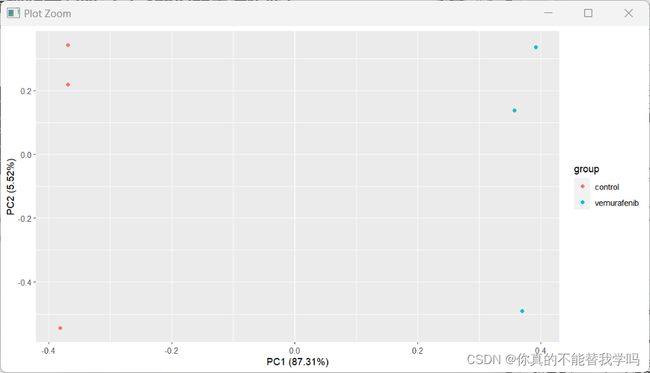
6.PCA

PCA即主成分分析，能够总结和可视化包含多个相互关联的定量变量所描述的个体、观测值的数据集中信息，每个变量都可以视为一个不同的维度。如果数据集中有3个以上的变量，则很难可视化多维超空间。主成分分析用于从多元数据表中提取重要信息，并将此信息表示为一组称为主成分的少量新变量。这些新变量对应于原始变量的线性组合。主成分的数量小于或等于原始变量的数量。给定数据集中的信息对应于其中包含的总变化。PCA的目标是识别数据变化最大的方向（或主要成分）。
换句话说，PCA将多元数据的维数减少为两个或三个主要成分，这些成分可以图形方式可视化，而信息丢失最少。

BiocManager::install("ggfortify")
library(ggfortify)
df=as.data.frame(t(exprSet))
df$group=group_list
autoplot(prcomp(df[,1:(ncol(df)-1)]),data=df,colour='group')

可以看到这个对照和处理组样品还是分得很开，说明表达矩阵没有问题。