多元线性回归数据集_《算法模型篇》——多元线性回归
我一度认为多元线性回归是统计学的终点。
还在中学的时候,我接触到了“数学模型”一词,那时觉得数学模型特别高大上,甚至觉得这是脱离了平面是一种三维立体的东西。尽管高中的时候就已经接触回归方程了,但那时根本没觉得这和数据模型有什么关系。后来本科的时候开始学多元线性回归,觉得这只是开了个头,后面肯定会教那种三维的立体的数学模型的,结果无论是统计学、概率论、计量通通最多都只教到多元回归。我不死心,去翻阅各类统计学教程,基本也都是教完多元回归书就戛然而止了。
研究生的时候仍然要学多元线性回归,但也知道了除了多元线性回归之外还有很多模型可以应用,但是以多元线性归回的易用性和可解释性来看,各行各业包括学术研究还是在广泛地使用多元线性回归,所以对大部分的人来说统计学的终点是多元线性回归其实也不算错。
除了多元线性回归具有方便使用和可解释性强的优点外,我们为什么还是要学习多元线性回归呢,直接用各种最新最前沿的模型不可以吗?
如果要做类比的话,多元线性回归有点像牛顿的经典物理力学体系,学习牛顿的三条定律后可以解释低速宏观的各种现象,这就是其易用性和高可解释性,在这种场景下就没必要去考虑量子力学和相对论。而多元线性回归又是其他模型的基础,如后面会讲到的逻辑回归(logistics model),尽管是分类模型却是从多元线性回归演变过来的,所以学习多元线性回归,了解其基本思路和方法能够帮助我们打好基础然后进一步学习和应用其他模型。
小结一下就是,学习多元线性回归是因为其仍可被广泛应用在各种领域和场景并且具有很好的解释性,同时也是学习其他模型的基础。
啰嗦了一大串关于多元线性模型的背景后,下面开始正式讲解多元线性回归了。
还记得在《算法模型篇》——从雪糕店讲起里的一元线性回归吗?对多元线性回归最简单直接的解释就是从一元线性回归中的一个输入变量,或者叫自变量,拓展成多个输入变量。在本篇里我会用工业蒸汽量预测赛题与数据-天池大赛-阿里云天池里的数据一步步完成多元线性回归的建模,并按统计学派的统计假设检验的流程分析模型的有效性。如前所述,本篇更侧重于多元线性回归的应用,原理讲解和公式推导会被尽可能地压缩。
对“工业蒸汽量预测”的分析和建模流程如下:
1、数据概览
2、探索性性分析
3、建模和和优化
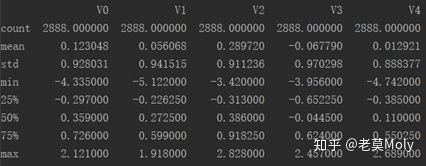
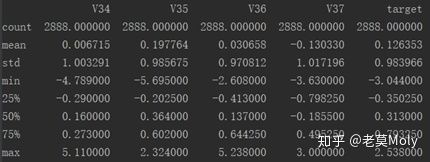
我们先来看一下数据长什么样子:
由于变量较多,故仅展示一部分总共有38个自变量,target是因变量,2888条数据,无缺失值,数据均经过脱敏处理。
由于后续我们将根据这些数据建立一个多元回归方程,变量之间的相关性就变得尤为重要,因此接下来进行相关性分析:
在R中用psych包中的corr.test函数分析target与其他变量之间的关系(默认的方法是pearson),尽管从统计假设上大部分变量都与target相关,但从相关系数来看显然有部分变量与target的相关性更高,此处阈值取0.55,有V0、V1、V2、V4、V8、V12、V27、V31、V37与target高度相关,后续模型中将很可能包含这几个变量。
另外还可通过corrplot包中的corrplot函数画出所有变量相关性的热力图,这会给后续分析和优化提供帮助。
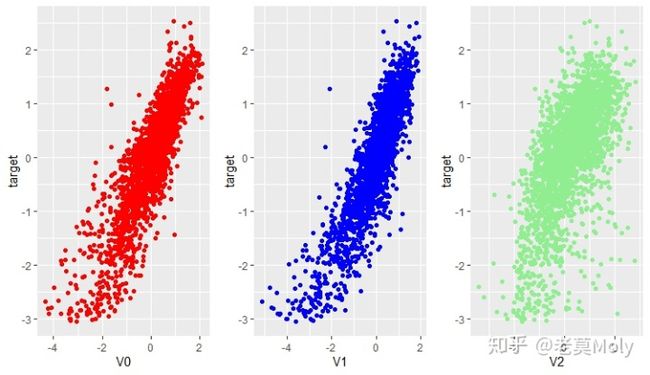
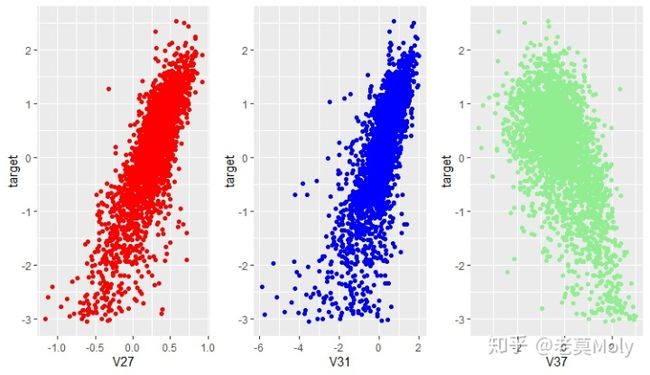
从相关性分析可知,V0、V1、V2、V4、V8、V12、V27、V31、V37与target存在某种联系,我们可以画出散点图来进一步观察这种相关性。当然,你也可以把38个自变量与target的散点图都画出来然后观察,但在本案例中自变量的数量较多,且仅从图像观察是不如通过相关性计算得到的结论准确,因此个人建议还是要先经过相关性分析再去进一步挖掘因变量和与其高度相关变量之间的关系。
通过观察9个与target高度相关变量的散点图,秉着大胆猜测小心求证的精神,可初步怀疑V1与target之间存在二次关系,并把V1的平方项纳入到模型的备选变量中去。
对各变量与target的关系有个整体认识后,可通过逐步回归的方法挑选合适的变量达成最佳的模型。这里需要提一下进行逐步回归时需要用到AIC(Akaike Information Criterion)赤池信息准则和BIC(Bayesian Information Criterion)贝叶斯信息准则,其中 :
是不是有点眼熟?还记得《算法模型篇》——基本思想1里提到的损失函数、经验风险和结构风险的概念吗?AIC或BIC本质上就是一个损失函数,
zqlrsr <- step(zqlr0,scope = formula(zqlr1),direction = 'both',k=log(nrow(zhengqi)))
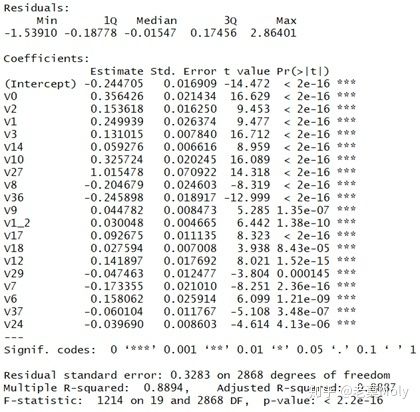
summary(zqlrsr)
zqlrsr_resid <- residuals(zqlrsr)
zqlrsr_fitted <- fitted(zqlrsr)在其基本面板上,我们主要考虑:
1、调整
2、
3、各变量对应的P值
从结果来看,调整
1、残差符合正态分布
2、独立性
3、同方差
4、多重共线性
让我们开始吧:
1、残差正态分布检验:
hist(zqlrsr_resid)
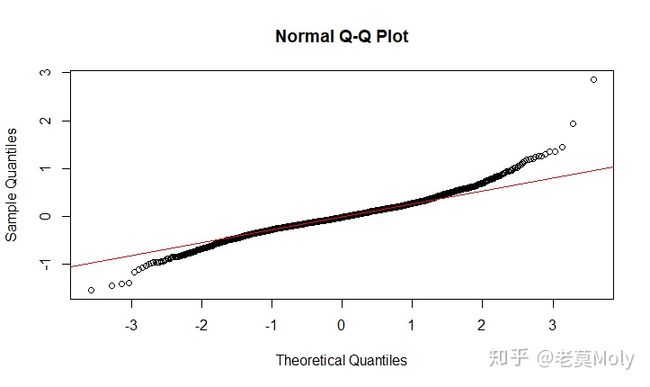
qqnorm(zqlrsr_resid)
qqline(zqlrsr_resid,col="red")
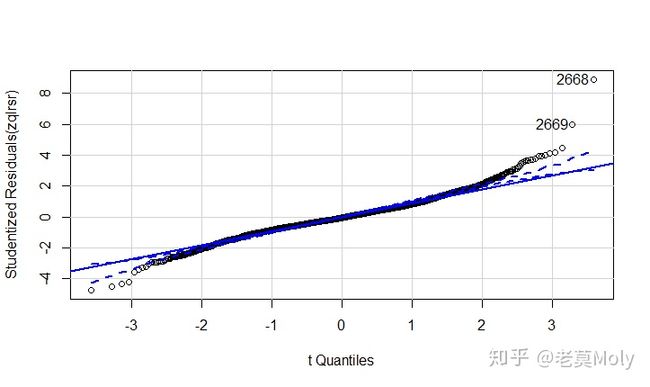
qqPlot(zqlrsr,id.method='identify',simulate = TRUE)从其正态分布检测图可知,其有较多的点并未分布在直线附近,甚至超过了可接受范围之外,因为可判断其残差不符合正态分布。
shapiro.test(zqlrsr_resid)
Shapiro-Wilk normality test
data: zqlrsr_resid
W = 0.96703, p-value < 2.2e-16
ks.test(zqlrsr_resid,y="rnorm")
One-sample Kolmogorov-Smirnov test
data: zqlrsr_resid
D = 4.691, p-value < 2.2e-16
alternative hypothesis: two-sidedShapiro-Wilktest test和Kolmogorov—Smimov test(原假设均为符合正态分布)同样支持该结论,其p值均小于0.05,故拒绝原假设,残差不符合正态分布。
2、独立性
lagdf <- function(x, k) {
c(rep(NA, k), x)[1 : length(x)]
}
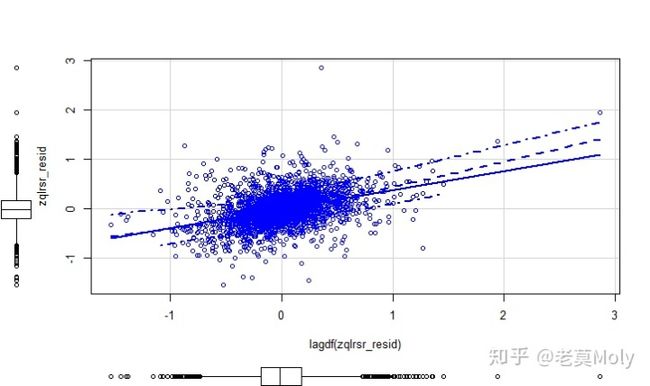
scatterplot(lagdf(zqlrsr_resid),zqlrsr_resid)
dwtest(zqlrsr)
Durbin-Watson test
data: zqlrsr
DW = 1.2343, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0采用Durbin-Watson test进行检验,p值小于0.05,故拒绝原假设,残差具有自相关性,同时这也可以从一阶残差自相关图上可以看出(这数据居然有自相关性!)。
3、同方差
ncvTest(zqlrsr)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 239.4814, Df = 1, p = < 2.22e-16p值小于0.05,故拒绝原假设,认为残差不符合同方差的假设
4、多重共线性
vif(zqlrsr)
V0 V2 V1 V3 V14 V10 V27 V8 V36
10.600451 5.874548 16.519590 1.550294 1.209625 10.295018 9.851246 13.003269 9.035703
V9 V1_2 V17 V18 V12 V29 V7 V6 V37
1.749809 2.441372 1.428894 1.196192 6.703426 4.696698 10.788097 15.163735 3.838548
V24
2.117329 方差扩大因子大于10的V0、V1、V10、V8、V7、V6与模型中的其他变量具有共线关系,需要考虑剔除或变换。
OK,一轮检测下来这个模型基本没通过哪个假设检验,哎,不过这其实挺正常的,不慌。由于数据经过脱敏,不妨先从解决多重共线性入手优化模型。
从原模型剔除掉V1、V6、V7、V8和V10,同时考虑到V1和V0存在强相关性,而V1的相关信息已经通过V1_2进行表达了,因此保留V0。剔除该四个变量后,模型的多重共线性已经消除了,但其他假设检验仍然未能通过,这很可能是数据本身或者模型选择所造成的,需要进行特征工程或者通过岭回归的方法来实现改进,但这部分已经超出了该篇的范畴了。
最后把逐步回归的模型以及剔除部分变量后的模型拿到线上进行检验,两个模型的线下MSE分别为0.107和0.122,线上的MSE则分别为2.2590和1.5204。从结果来看模型是过拟合了,但根据训练集和测试集的关系,在传统的多元回归模型的假设空间里MSE的优化空间已经比较有限,需要考虑选用别的模型来降低MSE。
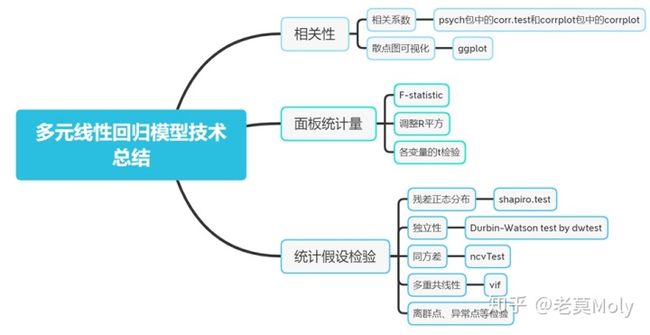
最后做一下技术总结: