机器学习实战刻意练习 —— Task 02. 朴素贝叶斯

机器学习实战刻意练习

第 1 周任务
  分类问题：K-邻近算法
  分类问题：决策树

第 2 周任务
  分类问题：朴素贝叶斯
  分类问题：逻辑回归

第 3 周任务
  分类问题：支持向量机

第 4 周任务
  分类问题：AdaBoost

第 5 周任务
  回归问题：线性回归、岭回归、套索方法、逐步回归等
  回归问题：树回归

第 6 周任务
  聚类问题：K均值聚类
  相关问题：Apriori

第 7 周任务
  相关问题：FP-Growth

第 8 周任务
  简化数据：PCA主成分分析
  简化数据：SVD奇异值分解
    

---

朴素贝叶斯

1.简介

  朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法 。
  最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型（Naive Bayesian Model，NBM）。和决策树模型相比，朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。同时，NBC模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。理论上，NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为NBC模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，这给NBC模型的正确分类带来了一定影响。

 1.1.贝叶斯定理

  条件概率 (conditional probability) 是指在事件 B 发生的情况下，事件 A 发生的概率。通常记为 P(A | B)。

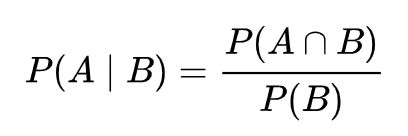
  因此

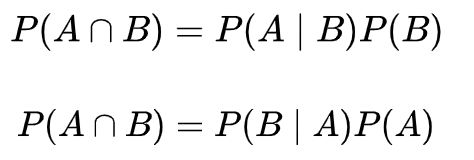
  可得

  由此可以推出贝叶斯公式

  这也是条件概率的计算公式。
  此外，由全概率公式，可得条件概率的另一种写法

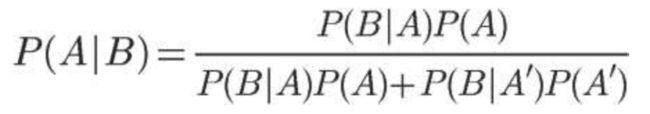
  其中样本空间由A和A’构成，由此求得事件B的概率。

 1.2.贝叶斯推断

  贝叶斯公式中，P(A)称为"先验概率"（Prior probability），即在B事件发生之前，对A事件概率的一个判断。
  P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，对A事件概率的重新评估。
  P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。
  所以，条件概率可以理解成下面的式子：后验概率＝先验概率 ｘ 调整因子
  这就是贝叶斯推断的含义。我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率"，由此得到更接近事实的"后验概率"。因为在分类中，只需要找出可能性最大的那个选项，而不需要知道具体那个类别的概率是多少，所以为了减少计算量，全概率公式在实际编程中可以不使用。

  而朴素贝叶斯推断，是在贝叶斯推断的基础上，对条件概率分布做了条件独立性的假设。因此可得朴素贝叶斯分类器的表达式。因为以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。

 1.3.模型概述

  朴素（指特征条件独立）贝叶斯方法，是指根据贝叶斯定理，对一个分类问题，给定样本特征x，样本属于类别y的概率是

  在这里，x是一个特征向量，将设x维度为M。因为朴素的假设，即特征条件独立，根据全概率公式展开，公式（1）可以表达为

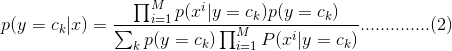
  这里，只要分别估计出，特征xⁱ在每一类的条件概率就可以了。类别y的先验概率可以通过训练集算出，同样通过训练集上的统计，可以得出对应每一类上的，条件独立的特征对应的条件概率向量。

 1.4.举个栗子~

  某个医院早上来了六个门诊的病人，他们的情况如下表所示：

症状	职业	疾病
打喷嚏	护士	感冒
打喷嚏	农夫	过敏
头痛	建筑工人	脑震荡
头痛	建筑工人	感冒
打喷嚏	教师	感冒
头痛	教师	脑震荡

   问：现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？

  根据贝叶斯定理：
  $$P(感冒|打喷嚏\ast 建筑工人)=\frac{P(打喷嚏\ast 建筑工人|感冒)}{P(打喷嚏\ast 建筑工人)}$$

根据朴素贝叶斯条件独立性的假设可知，"打喷嚏"和"建筑工人"这两个特征是独立的，因此，上面的等式就变成了
$$P(感冒|打喷嚏\ast 建筑工人)=\frac{P(打喷嚏|感冒)\ast P(建筑工人|感冒)\ast P(感冒)}{P(打喷嚏\ast 建筑工人)}$$

  通过计算得出
$$P(感冒|打喷嚏\ast 建筑工人)=\frac{0.66\ast 0.33\ast 0.5}{0.5\ast 0.33}=0.66$$

  因此，这个打喷嚏的建筑工人，有66%的概率是得了感冒。同理，可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率，就可以知道他最可能得什么病。

  这就是贝叶斯分类器的基本方法：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。

  同样，在编程的时候，如果不需要求出所属类别的具体概率，P(打喷嚏) = 0.5和P(建筑工人) = 0.33的概率是可以不用求的。

---

2. 动手实战

2.1. 项目案例1：屏蔽社区留言板的侮辱性言论

项目概述
  为了不影响社区的发展，我们要屏蔽侮辱性的言论，所以要构建一个快速过滤器，如果某条留言使用了负面或者侮辱性的语言，那么就将该留言标志为内容不当。过滤这类内容是一个很常见的需求。对此问题建立两个类型：侮辱类和非侮辱类，使用1和0分别表示。

开发流程
  我们把文本看成单词向量或者词条向量，也就是说将句子转换为向量。考虑出现所有文档中的单词，再决定将哪些单词纳入词汇表或者说所要的词汇集合，然后必须要将每一篇文档转换为词汇表上的向量。简单起见，我们先假设已经将本文切分完毕，存放到列表中，并对词汇向量进行分类标注。编写代码如下：

"""
函数说明:创建实验样本

Parameters:
    无
Returns:
    postingList - 实验样本切分的词条
    classVec - 类别标签向量
"""
def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],                #切分的词条
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]                                                                   #类别标签向量，1代表侮辱性词汇，0代表不是
    return postingList,classVec

if __name__ == '__main__':
    postingLIst, classVec = loadDataSet()
    for each in postingLIst:
        print(each)
    print(classVec)

  运行结果：

['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid']
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him']
['stop', 'posting', 'stupid', 'worthless', 'garbage']
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him']
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
[0, 1, 0, 1, 0, 1]

  从运行结果可以看出，我们已经将postingList是存放词条列表中，classVec是存放每个词条的所属类别，1代表侮辱类 ，0代表非侮辱类。


   继续编写代码，前面我们已经说过我们要先创建一个词汇表，并将切分好的词条转换为词条向量。

"""
函数说明:根据vocabList词汇表，将inputSet向量化，向量的每个元素为1或0

Parameters:
    vocabList - createVocabList返回的列表
    inputSet - 切分的词条列表
Returns:
    returnVec - 文档向量,词集模型
"""
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)                                    #创建一个其中所含元素都为0的向量
    for word in inputSet:                                                #遍历每个词条
        if word in vocabList:                                            #如果词条存在于词汇表中，则置1
            returnVec[vocabList.index(word)] = 1
        else: print("the word: %s is not in my Vocabulary!" % word)
    return returnVec                                                    #返回文档向量

"""
函数说明:将切分的实验样本词条整理成不重复的词条列表，也就是词汇表

Parameters:
    dataSet - 整理的样本数据集
Returns:
    vocabSet - 返回不重复的词条列表，也就是词汇表
"""
def createVocabList(dataSet):
    vocabSet = set([])                      #创建一个空的不重复列表
    for document in dataSet:               
        vocabSet = vocabSet | set(document) #取并集
    return list(vocabSet)

if __name__ == '__main__':
    postingList, classVec = loadDataSet()
    print('postingList:\n',postingList)
    myVocabList = createVocabList(postingList)
    print('myVocabList:\n',myVocabList)
    trainMat = []
    for postinDoc in postingList:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    print('trainMat:\n', trainMat)

  运行结果：

postingList:
 [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
myVocabList:
 ['maybe', 'him', 'steak', 'has', 'buying', 'stop', 'problems', 'how', 'quit', 'food', 'licks', 'flea', 'dog', 'my', 'please', 'take', 'so', 'ate', 'dalmation', 'to', 'garbage', 'mr', 'cute', 'I', 'help', 'worthless', 'is', 'posting', 'park', 'not', 'stupid', 'love']
trainMat:
 [[0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0], [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0], [0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0]]

  从运行结果可以看出，postingList是原始的词条列表，myVocabList是词汇表。myVocabList是所有单词出现的集合，没有重复的元素。词汇表是用来干什么的？没错，它是用来将词条向量化的，一个单词在词汇表中出现过一次，那么就在相应位置记作1，如果没有出现就在相应位置记作0。trainMat是所有的词条向量组成的列表。它里面存放的是根据myVocabList向量化的词条向量。

  我们已经得到了词条向量。接下来，我们就可以通过词条向量训练朴素贝叶斯分类器。

"""
函数说明:朴素贝叶斯分类器训练函数

Parameters:
    trainMatrix - 训练文档矩阵，即setOfWords2Vec返回的returnVec构成的矩阵
    trainCategory - 训练类别标签向量，即loadDataSet返回的classVec
Returns:
    p0Vect - 侮辱类的条件概率数组
    p1Vect - 非侮辱类的条件概率数组
    pAbusive - 文档属于侮辱类的概率
"""
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)                            #计算训练的文档数目
    numWords = len(trainMatrix[0])                            #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)        #文档属于侮辱类的概率
    p0Num = np.zeros(numWords); p1Num = np.zeros(numWords)    #创建numpy.zeros数组,词条出现数初始化为0
    p0Denom = 0.0; p1Denom = 0.0                            #分母初始化为0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:                            #统计属于侮辱类的条件概率所需的数据，即P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                                                #统计属于非侮辱类的条件概率所需的数据，即P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = p1Num/p1Denom                                      
    p0Vect = p0Num/p0Denom         
    return p0Vect,p1Vect,pAbusive                            #返回属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率

if __name__ == '__main__':
    postingList, classVec = loadDataSet()
    myVocabList = createVocabList(postingList)
    print('myVocabList:\n', myVocabList)
    trainMat = []
    for postinDoc in postingList:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNB0(trainMat, classVec)
    print('p0V:\n', p0V)
    print('p1V:\n', p1V)
    print('classVec:\n', classVec)
    print('pAb:\n', pAb)

  得到结果：

myVocabList:
 ['ate', 'is', 'mr', 'garbage', 'how', 'steak', 'take', 'help', 'maybe', 'dog', 'cute', 'please', 'flea', 'I', 'buying', 'quit', 'so', 'food', 'dalmation', 'park', 'worthless', 'stop', 'posting', 'love', 'my', 'to', 'problems', 'him', 'not', 'stupid', 'has', 'licks']
p0V:
 [0.04166667 0.04166667 0.04166667 0.         0.04166667 0.04166667
 0.         0.04166667 0.         0.04166667 0.04166667 0.04166667
 0.04166667 0.04166667 0.         0.         0.04166667 0.
 0.04166667 0.         0.         0.04166667 0.         0.04166667
 0.125      0.04166667 0.04166667 0.08333333 0.         0.
 0.04166667 0.04166667]
p1V:
 [0.         0.         0.         0.05263158 0.         0.
 0.05263158 0.         0.05263158 0.10526316 0.         0.
 0.         0.         0.05263158 0.05263158 0.         0.05263158
 0.         0.05263158 0.10526316 0.05263158 0.05263158 0.
 0.         0.05263158 0.         0.05263158 0.05263158 0.15789474
 0.         0.        ]
classVec:
 [0, 1, 0, 1, 0, 1]
pAb:
 0.5

  p0V存放的是每个单词属于类别0，也就是非侮辱类词汇的概率。比如p0V的倒数第6个概率，就是stupid这个单词属于非侮辱类的概率为0。同理，p1V的倒数第6个概率，就是stupid这个单词属于侮辱类的概率为0.15789474，也就是约等于15.79%的概率。我们知道stupid的中文意思是蠢货，难听点的叫法就是傻逼。显而易见，这个单词属于侮辱类。pAb是所有侮辱类的样本占所有样本的概率，从classVec中可以看出，一用有3个侮辱类，3个非侮辱类。所以侮辱类的概率是0.5。因此p0V存放的就是P(him|非侮辱类) = 0.0833、P(is|非侮辱类) = 0.0417，一直到P(dog|非侮辱类) = 0.0417，这些单词的条件概率。同理，p1V存放的就是各个单词属于侮辱类的条件概率。pAb就是先验概率。

  已经训练好分类器，接下来，使用分类器进行分类。

"""
函数说明:朴素贝叶斯分类器分类函数

Parameters:
	vec2Classify - 待分类的词条数组
	p0Vec - 侮辱类的条件概率数组
	p1Vec -非侮辱类的条件概率数组
	pClass1 - 文档属于侮辱类的概率
Returns:
	0 - 属于非侮辱类
	1 - 属于侮辱类
"""
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
	p1 = reduce(lambda x,y:x*y, vec2Classify * p1Vec) * pClass1    			#对应元素相乘
	p0 = reduce(lambda x,y:x*y, vec2Classify * p0Vec) * (1.0 - pClass1)
	print('p0:',p0)
	print('p1:',p1)
	if p1 > p0:
		return 1
	else: 
		return 0

"""
函数说明:测试朴素贝叶斯分类器

Parameters:
	无
Returns:
	无
"""
def testingNB():
	listOPosts,listClasses = loadDataSet()									#创建实验样本
	myVocabList = createVocabList(listOPosts)								#创建词汇表
	trainMat=[]
	for postinDoc in listOPosts:
		trainMat.append(setOfWords2Vec(myVocabList, postinDoc))				#将实验样本向量化
	p0V,p1V,pAb = trainNB0(np.array(trainMat),np.array(listClasses))		#训练朴素贝叶斯分类器
	testEntry = ['love', 'my', 'dalmation']									#测试样本1
	thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))				#测试样本向量化
	if classifyNB(thisDoc,p0V,p1V,pAb):
		print(testEntry,'属于侮辱类')										#执行分类并打印分类结果
	else:
		print(testEntry,'属于非侮辱类')										#执行分类并打印分类结果
	testEntry = ['stupid', 'garbage']										#测试样本2

	thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))				#测试样本向量化
	if classifyNB(thisDoc,p0V,p1V,pAb):
		print(testEntry,'属于侮辱类')										#执行分类并打印分类结果
	else:
		print(testEntry,'属于非侮辱类')										#执行分类并打印分类结果

if __name__ == '__main__':
	testingNB()

  运行结果：

p0: 0.0
p1: 0.0
['love', 'my', 'dalmation'] 属于非侮辱类
p0: 0.0
p1: 0.0
['stupid', 'garbage'] 属于非侮辱类

  你会发现，这样写的算法无法进行分类，p0和p1的计算结果都是0，这里显然存在问题。

2.2. 项目案例2：过滤垃圾邮件

  使用朴素贝叶斯解决一些现实生活中的问题时，需要先从文本内容得到字符串列表，然后生成词向量。下面这个例子中，我们将了解朴素贝叶斯的一个最著名的应用：电子邮件垃圾过滤。首先看一下使用朴素贝叶斯对电子邮件进行分类的步骤：

• 收集数据：提供文本文件。
• 准备数据：将文本文件解析成词条向量。
• 分析数据：检查词条确保解析的正确性。
• 训练算法：使用我们之前建立的trainNB0()函数。
• 测试算法：使用classifyNB()，并构建一个新的测试函数来计算文档集的错误率。
• 使用算法：构建一个完整的程序对一组文档进行分类，将错分的文档输出到屏幕上。

  数据下载点击这里，有两个文件夹ham和spam，spam文件下的txt文件为垃圾邮件。

import numpy as np
import random
import re

"""
函数说明:将切分的实验样本词条整理成不重复的词条列表，也就是词汇表

Parameters:
    dataSet - 整理的样本数据集
Returns:
    vocabSet - 返回不重复的词条列表，也就是词汇表
"""
def createVocabList(dataSet):
    vocabSet = set([])                      #创建一个空的不重复列表
    for document in dataSet:               
        vocabSet = vocabSet | set(document) #取并集
    return list(vocabSet)

"""
函数说明:根据vocabList词汇表，将inputSet向量化，向量的每个元素为1或0

Parameters:
    vocabList - createVocabList返回的列表
    inputSet - 切分的词条列表
Returns:
    returnVec - 文档向量,词集模型
"""
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)                                    #创建一个其中所含元素都为0的向量
    for word in inputSet:                                                #遍历每个词条
        if word in vocabList:                                            #如果词条存在于词汇表中，则置1
            returnVec[vocabList.index(word)] = 1
        else: print("the word: %s is not in my Vocabulary!" % word)
    return returnVec                                                    #返回文档向量


"""
函数说明:根据vocabList词汇表，构建词袋模型

Parameters:
    vocabList - createVocabList返回的列表
    inputSet - 切分的词条列表
Returns:
    returnVec - 文档向量,词袋模型
"""
def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList)                                        #创建一个其中所含元素都为0的向量
    for word in inputSet:                                                #遍历每个词条
        if word in vocabList:                                            #如果词条存在于词汇表中，则计数加一
            returnVec[vocabList.index(word)] += 1
    return returnVec                                                    #返回词袋模型

"""
函数说明:朴素贝叶斯分类器训练函数

Parameters:
    trainMatrix - 训练文档矩阵，即setOfWords2Vec返回的returnVec构成的矩阵
    trainCategory - 训练类别标签向量，即loadDataSet返回的classVec
Returns:
    p0Vect - 侮辱类的条件概率数组
    p1Vect - 非侮辱类的条件概率数组
    pAbusive - 文档属于侮辱类的概率
"""
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)                            #计算训练的文档数目
    numWords = len(trainMatrix[0])                            #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)        #文档属于侮辱类的概率
    p0Num = np.ones(numWords); p1Num = np.ones(numWords)    #创建numpy.ones数组,词条出现数初始化为1，拉普拉斯平滑
    p0Denom = 2.0; p1Denom = 2.0                            #分母初始化为2,拉普拉斯平滑
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:                            #统计属于侮辱类的条件概率所需的数据，即P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                                                #统计属于非侮辱类的条件概率所需的数据，即P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num/p1Denom)                            #取对数，防止下溢出         
    p0Vect = np.log(p0Num/p0Denom)         
    return p0Vect,p1Vect,pAbusive                            #返回属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率

"""
函数说明:朴素贝叶斯分类器分类函数

Parameters:
    vec2Classify - 待分类的词条数组
    p0Vec - 侮辱类的条件概率数组
    p1Vec -非侮辱类的条件概率数组
    pClass1 - 文档属于侮辱类的概率
Returns:
    0 - 属于非侮辱类
    1 - 属于侮辱类
"""
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)        #对应元素相乘。logA * B = logA + logB，所以这里加上log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

"""
函数说明:朴素贝叶斯分类器训练函数

Parameters:
    trainMatrix - 训练文档矩阵，即setOfWords2Vec返回的returnVec构成的矩阵
    trainCategory - 训练类别标签向量，即loadDataSet返回的classVec
Returns:
    p0Vect - 侮辱类的条件概率数组
    p1Vect - 非侮辱类的条件概率数组
    pAbusive - 文档属于侮辱类的概率
"""
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)                            #计算训练的文档数目
    numWords = len(trainMatrix[0])                            #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)        #文档属于侮辱类的概率
    p0Num = np.ones(numWords); p1Num = np.ones(numWords)    #创建numpy.ones数组,词条出现数初始化为1，拉普拉斯平滑
    p0Denom = 2.0; p1Denom = 2.0                            #分母初始化为2,拉普拉斯平滑
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:                            #统计属于侮辱类的条件概率所需的数据，即P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                                                #统计属于非侮辱类的条件概率所需的数据，即P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num/p1Denom)                            #取对数，防止下溢出         
    p0Vect = np.log(p0Num/p0Denom)         
    return p0Vect,p1Vect,pAbusive                            #返回属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率


"""
函数说明:接收一个大字符串并将其解析为字符串列表

Parameters:
    无
Returns:
    无
"""
def textParse(bigString):                                                   #将字符串转换为字符列表
    listOfTokens = re.split(r'\W*', bigString)                              #将特殊符号作为切分标志进行字符串切分，即非字母、非数字
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]            #除了单个字母，例如大写的I，其它单词变成小写

"""
函数说明:测试朴素贝叶斯分类器

Parameters:
    无
Returns:
    无
"""
def spamTest():
    docList = []; classList = []; fullText = []
    for i in range(1, 26):                                                  #遍历25个txt文件
        wordList = textParse(open('email/spam/%d.txt' % i, 'r').read())     #读取每个垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(1)                                                 #标记垃圾邮件，1表示垃圾文件
        wordList = textParse(open('email/ham/%d.txt' % i, 'r').read())      #读取每个非垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(0)                                                 #标记非垃圾邮件，1表示垃圾文件   
    vocabList = createVocabList(docList)                                    #创建词汇表，不重复
    trainingSet = list(range(50)); testSet = []                             #创建存储训练集的索引值的列表和测试集的索引值的列表                       
    for i in range(10):                                                     #从50个邮件中，随机挑选出40个作为训练集,10个做测试集
        randIndex = int(random.uniform(0, len(trainingSet)))                #随机选取索索引值
        testSet.append(trainingSet[randIndex])                              #添加测试集的索引值
        del(trainingSet[randIndex])                                         #在训练集列表中删除添加到测试集的索引值
    trainMat = []; trainClasses = []                                        #创建训练集矩阵和训练集类别标签系向量             
    for docIndex in trainingSet:                                            #遍历训练集
        trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))       #将生成的词集模型添加到训练矩阵中
        trainClasses.append(classList[docIndex])                            #将类别添加到训练集类别标签系向量中
    p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses))  #训练朴素贝叶斯模型
    errorCount = 0                                                          #错误分类计数
    for docIndex in testSet:                                                #遍历测试集
        wordVector = setOfWords2Vec(vocabList, docList[docIndex])           #测试集的词集模型
        if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:    #如果分类错误
            errorCount += 1                                                 #错误计数加1
            print("分类错误的测试集：",docList[docIndex])
    print('错误率：%.2f%%' % (float(errorCount) / len(testSet) * 100))


if __name__ == '__main__':
    spamTest()

  函数spamTest()会输出在10封随机选择的电子邮件上的分类错误概率。既然这些电子邮件是随机选择的，所以每次的输出结果可能有些差别。如果发现错误的话，函数会输出错误的文档的此表，这样就可以了解到底是哪篇文档发生了错误。如果想要更好地估计错误率，那么就应该将上述过程重复多次，比如说10次，然后求平均值。相比之下，将垃圾邮件误判为正常邮件要比将正常邮件归为垃圾邮件好。

---

参考资料

• https://www.cnblogs.com/geo-will/p/10468401.html
• https://blog.csdn.net/tanhongguang1/article/details/45016421
• https://blog.csdn.net/LSGO_MYP/article/details/103111698
• https://blog.csdn.net/c406495762/article/details/77341116
• https://blog.csdn.net/c406495762/article/details/77500679