【交通流预测】《Graph WaveNet for Deep Spatial-Temporal Graph Modeling》论文详解

点击论文下载链接
点击代码下载链接

---

文章总结

• - 现存问题：

  ① 捕获空间关系： 现有的方法大多捕捉对固定图结构的空间依赖性。然而，这种固定图结构不一定反应真实站点间的空间依赖关系，并且由于数据中不完整的连接，可能会丢失真正的关系。
  ② 捕获时间关系：现存方法不能很好的捕获较长的时间序列（>30min）。

• - 文章贡献点：
  ① 构建自适应的邻接矩阵: 本文提出的自适应邻接矩阵能够在没有任何先验知识的指导下从数据中自动发现未见过的图形结构。
  ② 提出新的模型框架：GCN+扩散因果卷积。

一、Abstract

  时空图建模是分析系统中组件的空间关系和时间趋势的重要任务。假设实体之间的潜在关系是预先确定的，现有的方法大多捕捉对固定图结构的空间依赖性。然而，显式图结构(关系)不一定选择依赖关系，并且由于数据中不完整的连接，可能会丢失真正的关系。此外，现有方法对于捕捉时间趋势是无效的，因为这些方法中使用的CNN或RNN不能很好地捕捉长程时间序列。为了克服这些限制，我们在本文中提出了一种新的用于时空图建模的图神经网络结构——Graph WaveNet。通过开发一种新的自适应依赖矩阵并通过节点嵌入来学习它，我们的模型可以精确地捕获数据中隐藏的空间依赖。由于叠加的扩张1D卷积成分的感受野随着层数的增加呈指数增长，Graph WaveNet能够处理非常长的序列。这两个组件无缝集成在一个统一的框架中，整个框架是以端到端的方式学习的。在METR-LA 和 PEMS-BAY两个公共交通网络数据集上的实验结果证明了该算法的优越性能。

---

二、Introduction

  随着图神经网络的发展，时空图建模越来越受到重视。它旨在通过假设连接节点之间的相互依赖性来建模动态节点级输入，如图所示。时空图建模在解决交通速度预测等复杂系统问题中有着广泛的应用。

  举一个具体的例子，在交通速度预测中，城市道路上的速度传感器形成一个图，其中边缘权重由两个节点的欧几里德距离来判断。由于一条道路上的交通拥堵可能导致其进入道路上的交通速度降低，因此在对每条道路上的交通速度的时间序列数据建模时，自然会将交通系统的底层图结构视为节点之间相互依赖关系的先验知识。

  时空图建模背后的一个基本假设是，节点的未来信息取决于其历史信息以及其邻居的历史信息。因此，如何同时捕捉空间和时间相关性成为一个主要挑战。时空图建模的最新研究主要遵循两个方向： 将图卷积网络(GCN)集成到递归神经网络(RNN)中或集成到卷积神经网络(CNN)。虽然已经展示了将数据的图结构引入模型的有效性，但是这些方法面临两个主要缺点。

  ① 这些研究是假设数据的图结构反映了节点之间真正的依赖关系。然而，当一个连接不需要两个节点之间的相互依赖关系时，以及当两个节点之间的相互依赖关系缺失时，就会出现这种情况。举一个例子，让我们考虑一个推荐系统。在第一种情况下，两个用户是有联系的，但是他们可能对产品有不同的偏好。第二种情况就是两个用户可能有同样的偏好，但是却没有联系。Zhang et al.使用注意机制来解决第一种情况，即调整两个连接节点之间的依赖权重。但他们没有考虑到第二种情况。
  ② 目前对空间-时间图形建模的研究对学习时间依赖性是无效的。基于RNN的方法在捕捉长距离序列时存在耗时的迭代传播和梯度爆炸/消失问题。相反，基于CNN的方法享有并行计算、稳定梯度和低内存要求的优势。然而，这些工作需要使用许多层，以便捕捉很长的序列，因为它们采用标准的一维卷积，其感受野的大小随着隐藏层数量的增加而线性增长。

  本文提出了一个基于CNN的方法，名为Graph WaveNet，它解决了我们前面提到的两个缺点。我们提出了一个图卷积层，其中自适应邻接矩阵可以通过端到端监督训练从数据中学习。通过这种方式，自适应邻接矩阵保留了隐藏的空间依赖关系。受到WaveNet的启发，我们采用了堆叠扩张的随机卷积来捕捉时间依赖性。随着隐藏层数量的增加，堆叠扩张随意卷积网络的感受野大小呈指数级增长。有了堆叠扩张随意卷积的支持，Graph WaveNet能够高效地处理具有长距离时间序列的空间-时间图数据。

---

三、Methodology

1. Problem Definition

• 图表示：$G=(V,E)$，节点为V，边为E，邻接矩阵：$\mathbf{A}\in {\mathbf{R}}^{N\times N}$（N个节点）；
• 输入矩阵：${\mathbf{X}}^{(\mathbf{t})}\in {\mathbf{R}}^{N\times D}$（时间步为t）；
• 预测映射：给定一个图G及其历史S步图信号，学习映射关系f，它能够预测下一个T步图信号：$\left[{\mathbf{X}}^{(t-S):t},G\right]\stackrel{f}{\to }{\mathbf{X}}^{(t+1):(t+T)}$

---

2. Graph Convolution Layer

  图卷积是在给定节点结构信息的情况下提取节点特征的基本操作，从基于空间的角度来看，它通过聚集和转换节点的邻域信息来平滑节点的信号。他们的方法的优点是它是一个合成层，它的过滤器在空间中定位，并且它支持多维输入。

[1] Graph convolution layer:
$$\mathbf{Z}=\tilde{\mathbf{A}}\mathbf{X}\mathbf{W}$$
[2] diffusion convolution layer（扩散卷积）:
$$\mathbf{Z}=\sum _{k=0}^K{\mathbf{P}}^k\mathbf{X}{\mathbf{W}}_{\mathbf{k}}$$

[3] diffusion graph convolution layer （扩散卷积层）:
$\mathbf{Z}={\sum }_{k=0}^K{\mathbf{P}}_f^k\mathbf{X}{\mathbf{W}}_{k1}+{\mathbf{P}}_b^k\mathbf{X}{\mathbf{W}}_{k2}$
[4] Self-adaptive Adjacency Matrix （自适应邻接矩阵）:
$${\tilde{\mathbf{A}}}_{adp}=\mathrm{Soft}\mathrm{Max}\left(\mathrm{Re}LU\left({\mathbf{E}}_1{\mathbf{E}}_2^T\right)\right)$$

[5] Graph convolution layer （图卷积层）:
$$\mathbf{Z}=\sum _{k=0}^K{\mathbf{P}}_f^k\mathbf{X}{\mathbf{W}}_{k1}+{\mathbf{P}}_b^k\mathbf{X}{\mathbf{W}}_{k2}+{\tilde{\mathbf{A}}}_{apt}^k\mathbf{X}{\mathbf{W}}_{k3}$$
  我们使用ReLU激活函数来消除弱连接。采用SoftMax函数对自适应邻接矩阵进行归一化处理。因此，归一化自适应邻接矩阵可以看作是隐藏扩散过程的转移矩阵。通过结合预定义的空间依赖和自学习的隐藏图依赖，我们提出了以下图卷积层

[6] Graph convolution layer （图卷积层：当图形结构不可用时，我们建议仅使用自适应邻接矩阵来捕获隐藏的空间依赖）:
$$\mathbf{Z}=\sum _{k=0}^K{\tilde{\mathbf{A}}}_{apt}^k\mathbf{X}{\mathbf{W}}_k$$

---

3. Temporal Convolution Layer

  时间卷积层使用的是扩张的因果卷积文章

• 因果卷积简介：要处理序列问题（即要考虑时间问题）就不能使用普通的CNN卷积，必须使用新的CNN模型，这个就是因果卷积的作用。
  
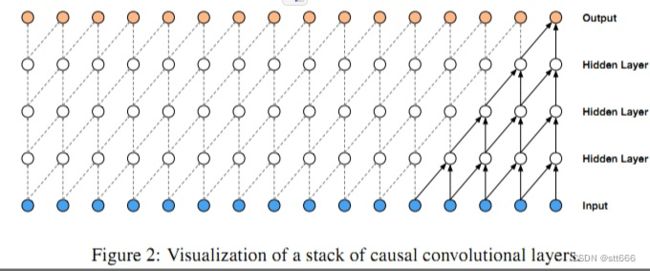
• 扩张因果卷积简介：如果我要考虑很久之前的变量x，那么卷积层数就必须增加。卷积层数的增加就带来：梯度消失，训练复杂，拟合效果不好的问题，为了决绝这个问题，出现了扩张卷积（dilated）。通过跳过部分输入来使filter可以应用于大于filter本身长度的区域，等同于通过增加零来从原始filter中生成更大的filter。
  
    与基于RNN的方法相反，扩展的随机卷积网络能够以非递归的方式正确处理长程序列，这有助于并行计算并缓解梯度爆炸问题。扩展的因果卷积通过在输入中填充零来保持时间因果顺序，以便对当前时间步长所做的预测仅涉及历史信息。作为标准1D卷积的一种特殊情况，扩展的因果卷积运算通过跳过某一步的值而在输入上滑动，
  [7] Dilated causal convolution operation （扩张因果卷积）:
  $$\mathbf{x}\star \mathbf{f}(t)=\sum _{s=0}^{K-1}\mathbf{f}(s)\mathbf{x}(t-d\times s)$$
• d: 每次跳跃/间隔的距离;
• f: 是卷积核。

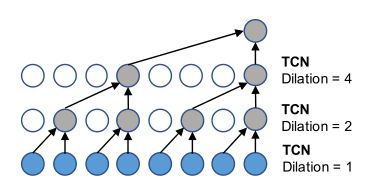
[7] Gated TCN（门控TCN）:
$$\mathbf{h}=g\left({\mathbf{\Theta }}_1\star \mathcal{X}+\mathbf{b}\right)\odot \sigma \left({\mathbf{\Theta }}_2\star \mathcal{X}+\mathbf{c}\right)$$
  为了有效控制信息流 学习更复杂时间维度的依赖关系，采用 Gated TCN 结构。

---

4. Framework of Graph WaveNet

  WaveNet的框架：它由堆叠的时空层和输出层组成。时空层由图卷积层(GCN)和门控时域卷积层(TCN)构成，该层由两个并行时域卷积层(TCN- a和TCN-b)组成。通过叠加多个时空层，Graph WaveNet能够处理不同时间层次的空间依赖关系。例如，底层的GCN接收短期的时间信息，而顶层的GCN处理长期的时间信息。

---

四、Experiments

1. 数据集

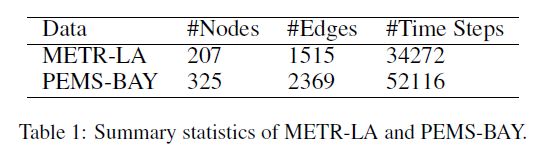
  ① METR-LA：记录了洛杉矶县高速公路上207个传感器四个月的交通速度统计数据;
  ② PEMS-BAY: 包含了加州海湾地区高速公路上325个传感器六个月的交通速度信息。

• 传感器的读数被汇总成5分钟的窗口；
• 节点的邻接矩阵由路网距离和阈值高斯核（thresholded Gaussian kernel）构造；
• 70%用于训练集，10%用于验证集，20%用于测试集。
  

2. Experimental Setups

• 为了覆盖输入序列的长度，使用了8层Graph WaveNet，其中包含了1、2、1、2、1、2、1、2的dilation因子序列。
• 通过大小为10的均匀分布随机初始化节点嵌入；
• Adam优化器；
• initial learning rate = 0.001；
• 对图卷积层的输出应用Dropout, p=0.3；
• 评价指标包括平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)。

3. Experimental Results

  对比结果：Graph WaveNet在两个数据集上都得到了较好的结果。它优于包括ARIMA、FCLSTM和WaveNet在内的时间模型。与其他时空模型相比，Graph WaveNet显著优于以往基于卷积的方法STGCN，同时也优于基于递归的方法DCRNN和GGRU。对于Table 2 所示的第二最佳模型GGRU, Graph WaveNet在15分钟的视界上较GGRU有小幅改进。然而，在60分钟的范围内实现更大的增强。我们认为这是因为我们的体系结构在每个时间阶段都更有能力检测空间依赖关系。GGRU使用循环架构，其中GCN层的参数在所有循环单元之间共享。而Graph WaveNet则采用堆叠的时空层，其中包含具有不同参数的独立GCN层。因此，Graph WaveNet中的每一个GCN层都能够聚焦于它自己的时间输入范围。

  自适应邻接矩阵的影响：为了验证自适应邻接矩阵的有效性，文章使用图WaveNet进行了五种不同邻接矩阵配置的实验。Table 3 显示了12个预测区间内MAE、RMSE和MAPE的平均得分。我们发现，在平均MAE下，自适应模型比前向模型效果更好。当图结构不可用时，graph WaveNet仍然能够实现良好的性能。前向-后向自适应模型在所有三个评估指标上得分最低。这表明，在给定图结构信息的情况下，加入自适应邻接矩阵可以为模型引入新的有用信息。

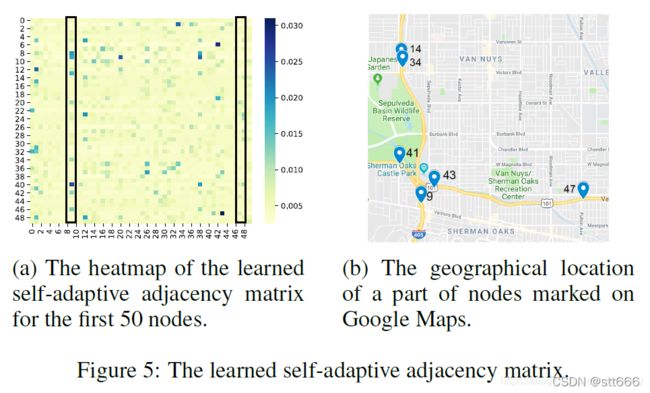
  自适应邻接矩阵的影响：进一步研究了在METR-LA数据集上训练的forward-backward-adaptive model配置下学习到的自适应邻接矩阵。从图5a中可以看出，有些列的高值点比其他列的高值点多，如左框中的第9列，右框中的第47列。说明图中一些节点对大多数节点有影响，而另一些节点影响较小。图5b证实了我们的观察。可以看出，节点9位于多条主干道的交叉口附近，而节点47位于一条单行道上。

  Computation Time：WaveNet的运行速度比DCRNN快5倍，但比STGCN慢2倍。为了进行推断，我们在验证数据上测量每个模型的总时间成本。在推理阶段，Graph WaveNet是最有效的。

五、 Conclusion

  本文提出了一种新的时空图建模模型。我们的模型通过结合图卷积和扩展的偶然卷积来有效地捕捉时空相关性。我们提出了一种从数据中自动学习隐藏空间相关性的有效方法。这为时空图建模开辟了一个新的方向，在这个领域中，系统的依赖结构是未知的，但需要发现。在两个公共交通网络数据集上，Graph WaveNet实现了最先进的结果。在未来的工作中，我们将研究在大规模数据集上应用Graph WaveNet的可扩展方法，并探索学习动态空间相关性的方法。