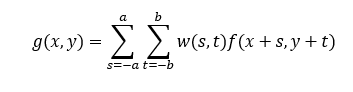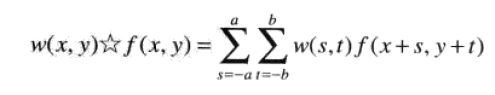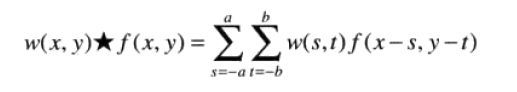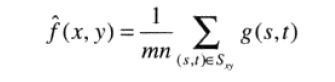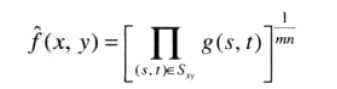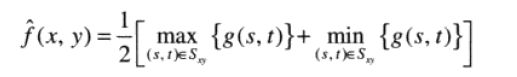matlab 空域滤波,MATLAB--空域滤波学习笔记

空域滤波

空域滤波是指对图像中每个像素为中心的邻域进行预定义操作，然后用得到的结果代替邻域中心像素点的像素值。滤波器的中心访问输入图像中的每个像素，就生成了滤波后的图像。

空域滤波器可分为线性空域滤波器和非线性空域滤波器。如果在图像像素上执行的是线性操作，则该滤波器称为线性空间滤波器，否则，滤波器就称为非线性空间滤波器。

1、线性空域滤波

我们关注奇数尺寸m×n(假设m=2a+1且n=2b+1)的滤波器，因为滤波器的中心落在整数值上。

一般来说，使用大小为m×n的滤波器对大小为M×N的图像进行线性空间滤波，可由下式表示：

其中，w(s,t)是滤波器系数，g(x,y)是滤波器系数与由该滤波器包围的图像像素的乘积之和。x和y是可变的，以便w中的每个像素可访问f中的每个像素。

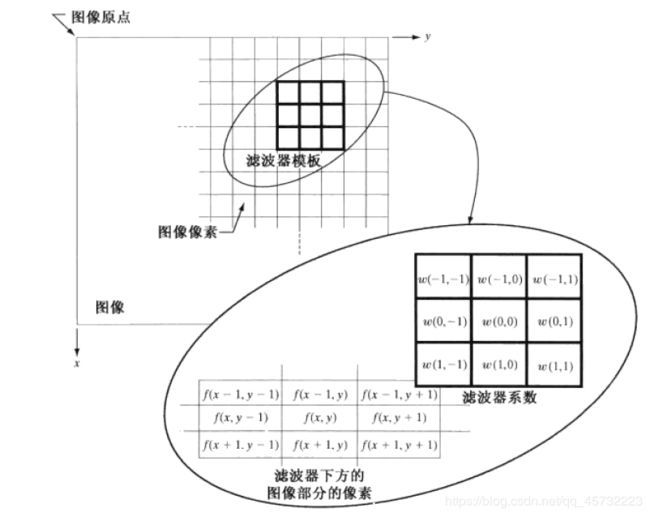
使用3×3的滤波器模板线性空间滤波的机理：

空间相关与卷积：相关是滤波器模板移过图像并计算每个位置乘积之和的处理。卷积的机理类似，但滤波器首先要旋转180°。因此，如果滤波器模板是对称的，相关和卷积将得到相同的结果。

相关：

卷积：

对相关运算讨论可得：

1、相关是滤波器位移的函数。即相关的第一个值对应于滤波器的零位移，第二个值对应于一个单位位移，等等。

2、滤波器w与离散单位冲激(包含全部0和单个1的函数)相关，得到的结果是w的一个拷贝，但旋转了180°。

对于大小为m×n的滤波器，我们在图像的顶部和底部至少填充m-1行0，在左侧和右侧填充n-1列0，得到相关结果的过程如下：

使用相关或卷积执行空间滤波是优先选择的方法。

在MATLAB中，进行图像的滤波时，可以采用函数imfilter()进行模板和图像的邻域相卷积的操作，还可以用函数conv2()进行二维卷积操作，还可以通过函数filter2()进行二维线性数字滤波，函数fspecial()产生滤波器模板。

常用的线性空域滤波器----均值滤波器

均值滤波器实际上是一种低通滤波器，这种处理结果降低了图像灰度的“尖锐”变化，然而，由于图像边缘也是由图像灰度尖锐变化带来的特性，所以均值滤波处理还是存在着不希望有的边缘模糊的负面效应。

(1)算术均值滤波器

算术均值滤波器平滑一幅图像中的局部变化，虽然模糊了结果，但降低了噪声。

(2)几何均值滤波器

几何均值滤波器实现的平滑可与算术均值滤波器相比，但这种处理中丢失的图像细节更少。

(3)谐波均值滤波器

谐波均值滤波器对于盐粒噪声效果较好，但不适用于胡椒噪声。它善于处理像高斯噪声那样的其他噪声。

(4)逆谐波均值滤波器

其中Q称为滤波器的阶数。这种滤波器适合减少或在实际中消除椒盐噪声的影响。当Q值为正时，该滤波器消除胡椒噪声；当Q值为负时，该滤波器消除盐粒噪声，但它不能同时消除这两种噪声。

当Q=0时，逆谐波均值滤波器简化为算术均值滤波器；而当Q=﹣1时，则为谐波均值滤波器。

总之，算术均值滤波器和几何均值滤波器(尤其是后者)更适合于处理高斯或均匀随机噪声。逆谐波均值滤波器更适合于处理脉冲噪声，但它还有一个缺点，即必须知道噪声是暗噪声还是亮噪声，以便于为Q选择正确的符号。如果Q符号选择错了，则可能会引起灾难性的后果。

2、非线性空域滤波

非线性空域滤波主要包括统计排序滤波和自适应滤波等。

统计排序滤波器

在MATLAB中，采用函数ordfilt2()进行排序滤波。函数ordfilt2()进行滤波时，可以通过模板来选择排序后的某个值作为输出。当函数ordfilt2()的调用形式为J=ordfilt2(I,median(1:m*n),[m,n])时，相当于中值滤波。

(1)中值滤波器

最著名的统计排序滤波器是中值滤波器，中值滤波是一种保护边缘的非线性图像平滑方法，非常适合去除图像中的椒盐噪声，在存在单极或双极脉冲噪声的情况下，中值滤波器尤其有效，平滑效果优于均值滤波，在抑制噪声的同时还能够保持图像的边缘清晰。中值滤波的主要功能是使拥有不同灰度的点看起来更接近于它的相邻点。

在MATLAB中，采用函数medfilt2()进行图像的二维中值滤波。

(2)最大值和最小值滤波器

最大值滤波器对于发现图像中的最亮点非常有用。因为胡椒噪声的值非常低，在这种最大值选择的过程中，可以降低它。

最小值滤波器对于发现图像中的最暗点非常有用。同样，作为最小值操作的结果，它可以降低盐粒噪声。

(3)中点滤波器

中点滤波器简单的计算滤波器包围区域中最大值和最小值之间的中点，即

这种滤波器结合了统计排序和求平均。它对于随机分布噪声工作得最好，如高斯噪声或均匀噪声。

(4)修正的阿尔法均值滤波器

自适应滤波器

(1)自适应局部降低噪声滤波器

(2)自适应中值滤波器

锐化空间滤波器

对于模糊的图像，通过锐化滤波器能够补偿图像的轮廓，让图像变得清晰。锐化滤波器常用拉普拉斯算子。拉普拉斯算子比较适合用于改善因为光线的漫反射造成的图像模糊。

拉普拉斯算子是各向同性微分算子，即旋转不变的。

一个二维图像函数f(x,y)的拉普拉斯算子定义为：

以离散形式来描述：

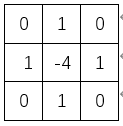
对应的滤波模板为：

拉普拉斯是一种微分算子，故其强调的是图像灰度中的突变，并不强调灰度级缓慢变化的区域。因此将原图像和拉普拉斯图像叠加在一起，可以复原背景特性并保持拉普拉斯锐化处理的效果。所以，我们使用拉普拉斯对图像锐化的基本方法可以表示为：

其中，f(x,y)和g(x,y)分别是输入图像和锐化后的图像。如果所使用的拉普拉斯滤波器模板中心系数为负，则常数C=-1;反之，常数C=1.

MATLAB实现

示例：

I=imread('rice.png');

I=im2double(I);

h=[0,1,0;1,-4,1;0,1,0];

J=conv2(I,h,'same');

K=I-J;

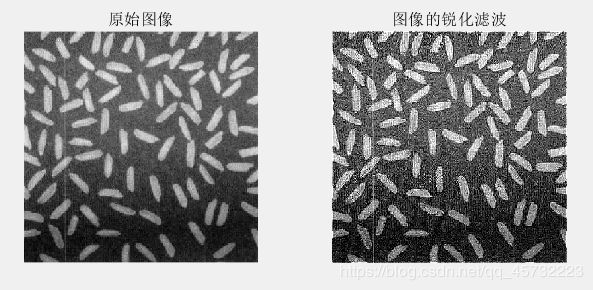
subplot(1,2,1); imshow(I); title('原始图像');

subplot(1,2,2); imshow(K); title('图像的锐化滤波');

运行结果：