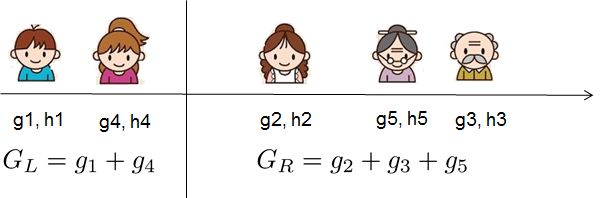XGBoost（极限梯度提升）

XGBoost 是一个优化的分布式梯度提升库，旨在高效、灵活和便携。它在Gradient Boosting框架下实现机器学习算法。XGBoost 提供了一种并行树提升（也称为 GBDT、GBM），可以快速准确地解决许多数据科学问题。相同的代码在主要的分布式环境（Kubernetes、Hadoop、SGE、MPI、Dask）上运行，可以解决数十亿个示例之外的问题。

XGBoost 代表“Extreme Gradient Boosting”，其中“Gradient Boosting”一词源自 Friedman 的论文Greedy Function Approximation: A Gradient Boosting Machine。

梯度增强树已经出现了一段时间，关于这个主题的材料很多。本教程将使用监督学习的元素以独立且有原则的方式解释提升树。我们认为这种解释更清晰、更正式，并激发了 XGBoost 中使用的模型公式。

监督学习的要素

XGBoost 用于监督学习问题，我们使用训练数据（具有多个特征）xi预测目标变量yi. 在我们具体了解树之前，让我们先回顾一下监督学习的基本要素。

型号及参数

监督学习中的模型通常是指预测所依据的数学结构yi由输入制成xi. 一个常见的例子是线性模型，其中预测为y^i=∑jθjxij，加权输入特征的线性组合。预测值可以有不同的解释，取决于任务，即回归或分类。例如，它可以进行逻辑转换以获得逻辑回归中正类的概率，也可以在我们对输出进行排名时用作排名分数。

参数是我们需要从数据中学习的未确定部分。在线性回归问题中，参数是系数θ. 通常我们会使用θ来表示参数（模型中有很多参数，我们这里的定义很草率）。

目标函数：训练损失+正则化

明智的选择yi，我们可以表达各种任务，例如回归、分类和排名。训练模型的任务相当于找到最佳参数θ最适合训练数据的xi和标签yi. 为了训练模型，我们需要定义目标函数 来衡量模型对训练数据的拟合程度。

目标函数的一个显着特征是它们由两部分组成：训练损失和正则化项：

obj(θ)=L(θ)+Ω(θ)

在哪里L是训练损失函数，并且Ω是正则化项。训练损失衡量我们的模型对训练数据的预测能力。一个常见的选择L是均方误差，由下式给出

L(θ)=∑i(yi−y^i)2

另一个常用的损失函数是逻辑损失，用于逻辑回归：

L(θ)=∑i[yiln⁡(1+e−y^i)+(1−yi)ln⁡(1+ey^i)]

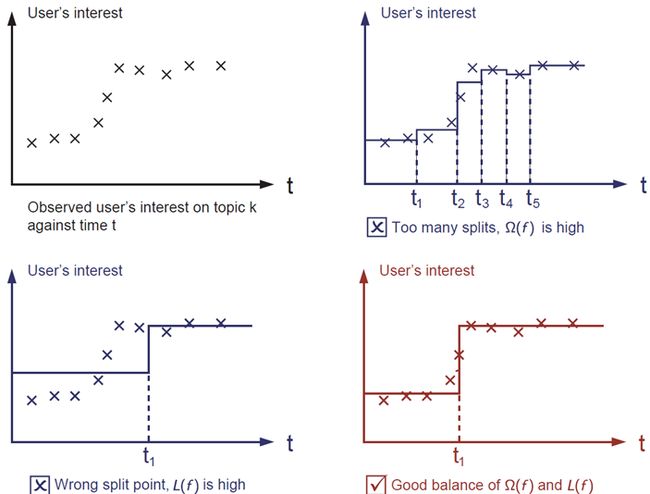
正则化项是人们通常忘记添加的内容。正则化项控制模型的复杂性，这有助于我们避免过度拟合。这听起来有点抽象，所以让我们考虑下图中的以下问题。给定图像左上角的输入数据点，要求您在视觉上拟合一个阶跃函数。您认为这三个解决方案中哪个最合适？

正确答案用红色标记。请考虑这在视觉上是否适合您。一般原则是我们既想要一个简单的预测模型。两者之间的权衡也称为机器学习中的偏差-方差权衡。

为什么要介绍一般原理？

上面介绍的元素构成了监督学习的基本元素，它们是机器学习工具包的自然构建块。例如，您应该能够描述梯度提升树和随机森林之间的差异和共同点。以形式化的方式理解这个过程也有助于我们理解我们正在学习的目标以及启发式方法背后的原因，例如修剪和平滑。

决策树集成

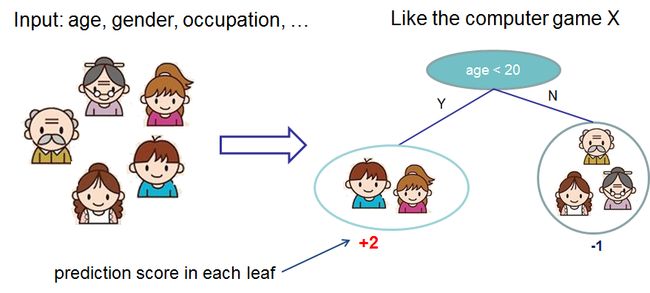
现在我们已经介绍了监督学习的元素，让我们从真正的树开始。首先，让我们先了解一下 XGBoost 的模型选择：决策树集成。树集成模型由一组分类和回归树 (CART) 组成。下面是一个简单的 CART 示例，它对某人是否会喜欢假设的电脑游戏 X 进行分类。

我们将一个家庭的成员分类为不同的叶子，并在相应的叶子上为他们分配分数。CART 与决策树有点不同，决策树的叶子只包含决策值。在 CART 中，真实分数与每个叶子相关联，这为我们提供了超越分类的更丰富的解释。正如我们将在本教程的后面部分中看到的那样，这也允许采用有原则的、统一的优化方法。

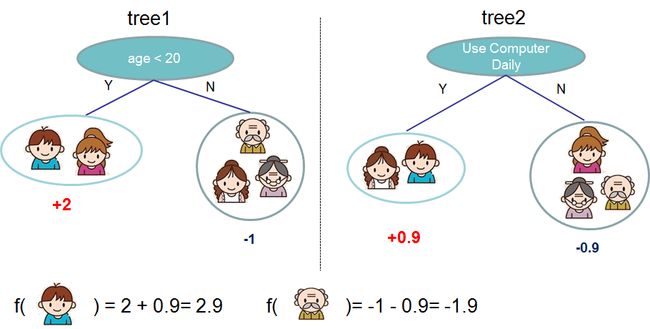
通常，一棵树的强度不足以在实践中使用。实际使用的是集成模型，它将多棵树的预测汇总在一起。

这是两棵树的树集合的示例。将每棵树的预测分数相加得到最终分数。如果你看一下这个例子，一个重要的事实是这两棵树试图相互补充。在数学上，我们可以将我们的模型写成以下形式

y^i=∑k=1Kfk(xi),fk∈F

在哪里K是树的数量，fk是函数空间中的函数F， 和F是所有可能的 CART 的集合。要优化的目标函数由下式给出

obj(θ)=∑inl(yi,y^i)+∑k=1Kω(fk)

在哪里ω(fk)是树的复杂度fk，稍后详细定义。

现在出现了一个棘手的问题：随机森林中使用的模型是什么？树组合！所以随机森林和提升树实际上是相同的模型；不同之处在于我们如何训练他们。这意味着，如果您为树集成编写预测服务，您只需要编写一个，它应该适用于随机森林和梯度提升树。（有关实际示例，请参阅Treelite 。）为什么监督学习的元素摇滚的一个例子。

树提升

现在我们介绍了模型，让我们转向训练：我们应该如何学习树？答案是，就像所有监督学习模型一样：定义一个目标函数并优化它！

让以下成为目标函数（记住它总是需要包含训练损失和正则化）：

obj=∑i=1nl(yi,y^i(t))+∑i=1tω(fi)

增材训练

我们要问的第一个问题：树的参数是什么？你会发现我们需要学习的就是那些函数fi，每个都包含树的结构和叶子分数。学习树结构比传统的优化问题要困难得多，传统的优化问题可以简单地采用梯度。一次学习所有的树是很困难的。相反，我们使用了一种加法策略：修复我们所学的内容，一次添加一棵新树。我们在步骤中写入预测值t作为y^i(t). 然后我们有

y^i(0)=0y^i(1)=f1(xi)=y^i(0)+f1(xi)y^i(2)=f1(xi)+f2(xi)=y^i(1)+f2(xi)…y^i(t)=∑k=1tfk(xi)=y^i(t−1)+ft(xi)

还有一个问题：每一步我们想要哪棵树？很自然的事情是添加一个优化我们的目标的。

obj(t)=∑i=1nl(yi,y^i(t))+∑i=1tω(fi)=∑i=1nl(yi,y^i(t−1)+ft(xi))+ω(ft)+constant

如果我们考虑使用均方误差 (MSE) 作为我们的损失函数，目标变为

obj(t)=∑i=1n(yi−(y^i(t−1)+ft(xi)))2+∑i=1tω(fi)=∑i=1n[2(y^i(t−1)−yi)ft(xi)+ft(xi)2]+ω(ft)+constant

MSE 的形式很友好，有一个一阶项（通常称为残差）和一个二次项。对于其他的兴趣损失（例如逻辑损失），要得到这么好的表格并不是那么容易。所以在一般情况下，我们将损失函数的泰勒展开式提升到二阶：

obj(t)=∑i=1n[l(yi,y^i(t−1))+gift(xi)+12hift2(xi)]+ω(ft)+constant

在哪里gi和hi被定义为

gi=∂y^i(t−1)l(yi,y^i(t−1))hi=∂y^i(t−1)2l(yi,y^i(t−1))

在我们删除所有常量之后，步骤的具体目标t变成

∑i=1n[gift(xi)+12hift2(xi)]+ω(ft)

这成为我们对新树的优化目标。该定义的一个重要优点是目标函数的值仅取决于gi和hi. 这就是 XGBoost 支持自定义损失函数的方式。我们可以使用完全相同的求解器优化每个损失函数，包括逻辑回归和成对排序gi和hi作为输入！

模型复杂度

我们已经介绍了训练步骤，但是等等，有一件重要的事情，正则化项！我们需要定义树的复杂度ω(f). 为了做到这一点，让我们首先细化树的定义f(x)作为

ft(x)=wq(x),w∈RT,q:Rd→{1,2,⋯,T}.

这里w是叶子上的分数向量，q是将每个数据点分配给相应叶的函数，并且T是叶子的数量。在 XGBoost 中，我们将复杂度定义为

ω(f)=γT+12λ∑j=1Twj2

当然，定义复杂性的方法不止一种，但这种方法在实践中效果很好。正则化是大多数树包处理得不那么小心的一部分，或者干脆忽略。这是因为传统的树学习处理只强调改进杂质，而复杂性控制则留给启发式。通过正式定义它，我们可以更好地了解我们正在学习什么，并获得在野外表现良好的模型。

结构分数

这是推导的神奇部分。重新制定树模型后，我们可以将目标值写为t-th 树为：

obj(t)≈∑i=1n[giwq(xi)+12hiwq(xi)2]+γT+12λ∑j=1Twj2=∑j=1T[(∑i∈Ijgi)wj+12(∑i∈Ijhi+λ)wj2]+γT

在哪里Ij={i|q(xi)=j}是分配给j-第叶。请注意，在第二行中，我们更改了求和的索引，因为同一叶子上的所有数据点都得到相同的分数。我们可以通过定义进一步压缩表达式Gj=∑i∈Ijgi和Hj=∑i∈Ijhi:

obj(t)=∑j=1T[Gjwj+12(Hj+λ)wj2]+γT

在这个等式中，wj相互独立，形式为Gjwj+12(Hj+λ)wj2是二次的，最好的wj对于给定的结构q(x)我们能得到的最好的客观减少是：

wj∗=−GjHj+λobj∗=−12∑j=1TGj2Hj+λ+γT

最后一个等式衡量树结构的好坏q(x)是。

如果这一切听起来有点复杂，让我们看一下图片，看看如何计算分数。基本上，对于给定的树结构，我们推送统计信息gi和hi到它们所属的叶子，将统计数据加在一起，并使用公式计算树的好坏。这个分数就像决策树中的杂质度量，只是它还考虑了模型的复杂性。

学习树结构

既然我们有一种方法来衡量一棵树的好坏，理想情况下我们会枚举所有可能的树并选择最好的树。在实践中这是难以处理的，因此我们将尝试一次优化树的一层。具体来说，我们尝试将一片叶子分成两片叶子，它得到的分数是

Gain=12[GL2HL+λ+GR2HR+λ−(GL+GR)2HL+HR+λ]−γ

这个公式可以分解为 1) 新左叶上的分数 2) 新右叶上的分数 3) 原始叶上的分数 4) 附加叶上的正则化。我们可以在这里看到一个重要的事实：如果增益小于γ，我们最好不要添加那个分支。这正是基于树的模型中的修剪技术！通过使用监督学习的原理，我们自然可以想出这些技术起作用的原因:)

对于实值数据，我们通常希望寻找最优分割。为了有效地做到这一点，我们将所有实例按排序顺序放置，如下图所示。

从左到右的扫描足以计算所有可能拆分解决方案的结构得分，我们可以有效地找到最佳拆分。

使用 xgboost 和 sklearn 的演示

from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_california_housing
import xgboost as xgb
import multiprocessing

if __name__ == "__main__":
    print("Parallel Parameter optimization")
    X, y = fetch_california_housing(return_X_y=True)
    xgb_model = xgb.XGBRegressor(n_jobs=multiprocessing.cpu_count() // 2)
    clf = GridSearchCV(xgb_model, {'max_depth': [2, 4, 6],
                                   'n_estimators': [50, 100, 200]}, verbose=1,
                       n_jobs=2)
    clf.fit(X, y)
    print(clf.best_score_)
    print(clf.best_params_)

使用 sklearn 接口访问 xgboost 评估指标的演示



 

import xgboost as xgb
import numpy as np
from sklearn.datasets import make_hastie_10_2

X, y = make_hastie_10_2(n_samples=2000, random_state=42)

# Map labels from {-1, 1} to {0, 1}
labels, y = np.unique(y, return_inverse=True)

X_train, X_test = X[:1600], X[1600:]
y_train, y_test = y[:1600], y[1600:]

param_dist = {'objective':'binary:logistic', 'n_estimators':2}

clf = xgb.XGBModel(**param_dist)
# Or you can use: clf = xgb.XGBClassifier(**param_dist)

clf.fit(X_train, y_train,
        eval_set=[(X_train, y_train), (X_test, y_test)],
        eval_metric='logloss',
        verbose=True)

# Load evals result by calling the evals_result() function
evals_result = clf.evals_result()

print('Access logloss metric directly from validation_0:')
print(evals_result['validation_0']['logloss'])

print('')
print('Access metrics through a loop:')
for e_name, e_mtrs in evals_result.items():
    print('- {}'.format(e_name))
    for e_mtr_name, e_mtr_vals in e_mtrs.items():
        print('   - {}'.format(e_mtr_name))
        print('      - {}'.format(e_mtr_vals))

print('')
print('Access complete dict:')
print(evals_result)

XGBoost 入门

import numpy as np
import scipy.sparse
import pickle
import xgboost as xgb
import os

# Make sure the demo knows where to load the data.
CURRENT_DIR = os.path.dirname(os.path.abspath(__file__))
XGBOOST_ROOT_DIR = os.path.dirname(os.path.dirname(CURRENT_DIR))
DEMO_DIR = os.path.join(XGBOOST_ROOT_DIR, 'demo')

# simple example
# load file from text file, also binary buffer generated by xgboost
dtrain = xgb.DMatrix(os.path.join(DEMO_DIR, 'data', 'agaricus.txt.train?indexing_mode=1'))
dtest = xgb.DMatrix(os.path.join(DEMO_DIR, 'data', 'agaricus.txt.test?indexing_mode=1'))

# specify parameters via map, definition are same as c++ version
param = {'max_depth': 2, 'eta': 1, 'objective': 'binary:logistic'}

# specify validations set to watch performance
watchlist = [(dtest, 'eval'), (dtrain, 'train')]
num_round = 2
bst = xgb.train(param, dtrain, num_round, watchlist)

# this is prediction
preds = bst.predict(dtest)
labels = dtest.get_label()
print('error=%f' %
      (sum(1 for i in range(len(preds)) if int(preds[i] > 0.5) != labels[i]) /
       float(len(preds))))
bst.save_model('0001.model')
# dump model
bst.dump_model('dump.raw.txt')
# dump model with feature map
bst.dump_model('dump.nice.txt', os.path.join(DEMO_DIR, 'data/featmap.txt'))

# save dmatrix into binary buffer
dtest.save_binary('dtest.buffer')
# save model
bst.save_model('xgb.model')
# load model and data in
bst2 = xgb.Booster(model_file='xgb.model')
dtest2 = xgb.DMatrix('dtest.buffer')
preds2 = bst2.predict(dtest2)
# assert they are the same
assert np.sum(np.abs(preds2 - preds)) == 0

# alternatively, you can pickle the booster
pks = pickle.dumps(bst2)
# load model and data in
bst3 = pickle.loads(pks)
preds3 = bst3.predict(dtest2)
# assert they are the same
assert np.sum(np.abs(preds3 - preds)) == 0

###
# build dmatrix from scipy.sparse
print('start running example of build DMatrix from scipy.sparse CSR Matrix')
labels = []
row = []
col = []
dat = []
i = 0
for l in open(os.path.join(DEMO_DIR, 'data', 'agaricus.txt.train')):
    arr = l.split()
    labels.append(int(arr[0]))
    for it in arr[1:]:
        k, v = it.split(':')
        row.append(i)
        col.append(int(k))
        dat.append(float(v))
    i += 1
csr = scipy.sparse.csr_matrix((dat, (row, col)))
dtrain = xgb.DMatrix(csr, label=labels)
watchlist = [(dtest, 'eval'), (dtrain, 'train')]
bst = xgb.train(param, dtrain, num_round, watchlist)

print('start running example of build DMatrix from scipy.sparse CSC Matrix')
# we can also construct from csc matrix
csc = scipy.sparse.csc_matrix((dat, (row, col)))
dtrain = xgb.DMatrix(csc, label=labels)
watchlist = [(dtest, 'eval'), (dtrain, 'train')]
bst = xgb.train(param, dtrain, num_round, watchlist)

print('start running example of build DMatrix from numpy array')
# NOTE: npymat is numpy array, we will convert it into scipy.sparse.csr_matrix
# in internal implementation then convert to DMatrix
npymat = csr.todense()
dtrain = xgb.DMatrix(npymat, label=labels)
watchlist = [(dtest, 'eval'), (dtrain, 'train')]
bst = xgb.train(param, dtrain, num_round, watchlist)

XGBoost 中的随机森林（TM）

XGBoost 通常用于训练梯度提升决策树和其他梯度提升模型。随机森林使用与梯度提升决策树相同的模型表示和推理，但训练算法不同。可以使用 XGBoost 来训练一个独立的随机森林，或者使用随机森林作为梯度提升的基础模型。在这里，我们专注于训练独立的随机森林。

从早期开始，我们就有用于训练随机森林的原生 API，以及 0.82 之后的新 Scikit-Learn 包装器（不包括在 0.82 中）。请注意，新的 Scikit-Learn 包装器仍处于实验阶段，这意味着我们可能会在需要时更改界面。

带有 XGBoost API 的独立随机森林

必须设置以下参数才能启用随机森林训练。

• booster应该设置为gbtree，因为我们正在训练森林。请注意，由于这是默认设置，因此无需显式设置此参数。

• subsample必须设置为小于 1 的值，以启用训练案例（行）的随机选择。

• 必须将参数之一colsample_by*设置为小于 1 的值才能启用随机选择列。通常，colsample_bynode将设置为小于 1 的值，以便在每个树拆分时随机抽样列。

• num_parallel_tree应该设置为正在训练的森林的大小。

• num_boost_round应设置为 1 以防止 XGBoost 增强多个随机森林。请注意，这是 的关键字参数train()，而不是参数字典的一部分。

• eta（别名：）learning_rate在训练随机森林回归时必须设置为 1。

• random_state可用于播种随机数生成器。

其他参数应该以与梯度提升类似的方式设置。例如，objective通常将reg:squarederror用于回归和 binary:logistic分类，lambda应根据所需的正则化权重等进行设置。

如果两者num_parallel_tree都num_boost_round大于 1，则训练将使用随机森林和梯度提升策略的组合。它将执行 回合，在每一回合num_boost_round中提升一个随机的树木森林。num_parallel_tree如果未启用提前停止，则最终模型将由 num_parallel_tree*num_boost_round树组成。

这是使用 xgboost 在 GPU 上训练随机森林的示例参数字典：

params = {
  'colsample_bynode': 0.8,
  'learning_rate': 1,
  'max_depth': 5,
  'num_parallel_tree': 100,
  'objective': 'binary:logistic',
  'subsample': 0.8,
  'tree_method': 'gpu_hist'
}

然后可以按如下方式训练随机森林模型：

bst = train(params, dmatrix, num_boost_round=1)

具有 Scikit-Learn-Like API 的独立随机森林

XGBRFClassifier并且XGBRFRegressor是提供随机森林功能的类似 SKL 的类。它们基本上是训练随机森林而不是梯度提升的版本，XGBClassifier并且XGBRegressor具有相应调整的某些参数的默认值和含义。尤其是：

• n_estimators指定要训练的森林的大小；它被转换为 num_parallel_tree, 而不是提升轮数

• learning_rate默认设置为 1

• colsample_bynode并且subsample默认设置为 0.8

• booster总是gbtree

举个简单的例子，你可以训练一个随机森林回归器：

from sklearn.model_selection import KFold

# Your code ...

kf = KFold(n_splits=2)
for train_index, test_index in kf.split(X, y):
    xgb_model = xgb.XGBRFRegressor(random_state=42).fit(
    X[train_index], y[train_index])

请注意，与 using 相比，这些类的参数选择更少 train()。特别是，使用此 API 将随机森林与梯度提升相结合是不可能的。

注意事项

• XGBoost 对目标函数使用二阶逼近。这可能导致与使用目标函数的精确值的随机森林实现不同的结果。

• XGBoost 在对训练用例进行二次采样时不执行替换。每个训练案例可以在子采样集中出现 0 次或 1 次。