回归预测 | MATLAB实现SSA-XGBoost(麻雀算法优化极限梯度提升树)多输入单输出
回归预测 | MATLAB实现SSA-XGBoost(麻雀算法优化极限梯度提升树)多输入单输出
目录
-
- 回归预测 | MATLAB实现SSA-XGBoost(麻雀算法优化极限梯度提升树)多输入单输出
-
- 预测效果
- 基本介绍
- 程序设计
- 参考资料
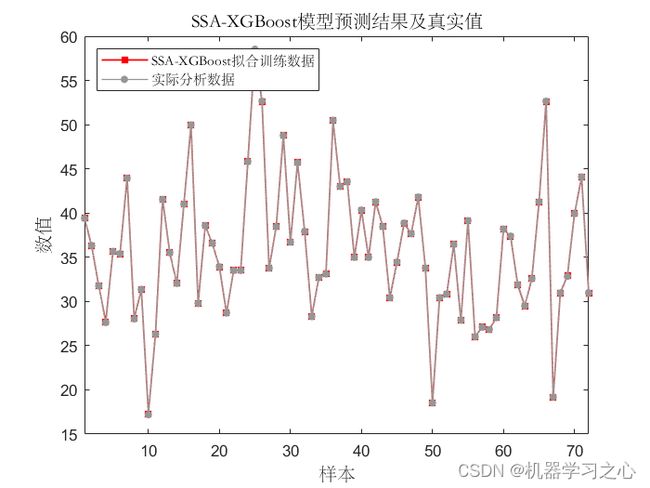
预测效果
基本介绍
麻雀搜索算法(Sparrow Search Algorithm, SSA)是于2020年提出的。SSA 主要是受麻雀的觅食行为和反捕食行为的启发而提出的。该算法比较新颖,具有寻优能力强,收敛速度快的优点。 算法流程:
Step1: 初始化种群,迭代次数,初始化捕食者和加入者比列。
Step2:计算适应度值,并排序。
Step3:利用式(3)更新捕食者位置。
Step4:利用式(4)更新加入者位置。
Step5:利用式(5)更新警戒者位置。
Step6:计算适应度值并更新麻雀位置。
Step7:是否满足停止条件,满足则退出,输出结果,否则,重复执行Step2-6;
xgboost是属于boosting家族,是GBDT算法的一个工程实现,在模型的训练过程中是聚焦残差,在目标函数中使用了二阶泰勒展开并加入了正则,在决策树的生成过程中采用了精确贪心的思路,寻找最佳分裂点的时候,使用了预排序算法,对所有特征都按照特征的数值进行预排序,然后遍历所有特征上的所有分裂点位,计算按照这些候选分裂点位分裂后的全部样本的目标函数增益,找到最大的那个增益对应的特征和候选分裂点位,从而进行分裂。
这样一层一层的完成建树过程, xgboost训练的时候,是通过加法的方式进行训练,也就是每一次通过聚焦残差训练一棵树出来,最后的预测结果是所有树的加和表示。本次优化的参数包括最大迭代次数,深度,学习率。
程序设计
- 完整代码和数据下载:SSA-XGBoost(麻雀算法优化极限梯度提升树)多输入单输出
%pop是种群,M是迭代次数,fobj是用来计算适应度的函数
%pNum是生产者
%r1==a
% r2:预警值
% fit:适应度
function [fMin , bestX,Convergence_curve ] = SSA(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim );
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x; % The individual's best position corresponding to the pFit
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
%
for t = 1 : M
[ ans, sortIndex ] = sort( pFit );% Sort.
[fmax,B]=max( pFit );
worse= x(B,:);
r2=rand(1);
%%%%%%%%%%%%%5%%%%%%这一部位为发现者(探索者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
if(r2<0.8)%预警值较小,说明没有捕食者出现
for i = 1 : pNum %r2小于0.8的发现者的改变(1-20) % Equation (3)
r1=rand(1);
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M));%对自变量做一个随机变换
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%对超过边界的变量进行去除
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) ); %就算新的适应度值
end
else %预警值较大,说明有捕食者出现威胁到了种群的安全,需要去其它地方觅食
for i = 1 : pNum %r2大于0.8的发现者的改变
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
end
%---------------------------------------------------------------------------------------------------------------------------
%%%%%%%%%%%%%5%%%%%%这一部位为加入者(追随者)的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
for i = ( pNum + 1 ) : pop %剩下20-100的个体的变换 % Equation (4)
A=floor(rand(1,dim)*2)*2-1;
if( i>(pop/2))%这个代表这部分麻雀处于十分饥饿的状态(因为它们的能量很低,也是是适应度值很差),需要到其它地方觅食
x( sortIndex(i ), : )=randn(1)*exp((worse-pX( sortIndex( i ), : ))/(i)^2);
else%这一部分追随者是围绕最好的发现者周围进行觅食,其间也有可能发生食物的争夺,使其自己变成生产者
x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);
end
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );%判断边界是否超出
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );%计算适应度值
end
%%%%%%%%%%%%%5%%%%%%这一部位为意识到危险(注意这里只是意识到了危险,不代表出现了真正的捕食者)的麻雀的位置更新%%%%%%%%%%%%%%%%%%%%%%%%%
c=randperm(numel(sortIndex));%%%%%%%%%这个的作用是在种群中随机产生其位置(也就是这部分的麻雀位置一开始是随机的,意识到危险了要进行位置移动,
%处于种群外围的麻雀向安全区域靠拢,处在种群中心的麻雀则随机行走以靠近别的麻雀)
%---------------------------------------------------------------------------------------------------------------------------
x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));
else %处于种群中心的麻雀的位置改变
x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);
end
x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );
end
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
end
end
Convergence_curve(t)=fMin;
end
%---------------------------------------------------------------------------------------------------------------------------
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
%---------------------------------------------------------------------------------------------------------------------------
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
%---------------------------------------------------------------------------------------------------------------------------
参考资料
[1] https://blog.csdn.net/category_11833757.html?spm=1001.2014.3001.5482
[2] https://blog.csdn.net/article/details/125125787
[3] https://blog.csdn.net/article/details/124928579