跟李沐学AI之现代卷积神经网络

现代卷积神经网络

对于最终模型精度影响来说，更大或更干净的数据集，稍微进行改进的特征提取，比任何学习算法带来的进步要大的多。

深度卷积学习网络 AlexNet

最火的机器学习是核方法，核心是特征提取，选择核函数来计算相关性，然后转换成凸优化问题，会有较好的定理，能够计算模型的复杂度。
在网络包含许多特征的深度模型需要大量的标签数据。训练可能需要数百个迭代轮数，对计算资源要求很高。AlexNet与LetNet在本质上没有任何区别。计算机视觉方法论的改变，之前专注于人工特征提取，但是后来利用CNN来进行学习特征，形成端到端的学习。


在最低层，模型学习到了一些类似于传统滤波器的特征提取器，AlexNet的更高层建立在这些底层表示的基础上，以表示更大的特征。最终的隐藏神经单元可以学习图像的综合表示，使得不同类别的数据易于区分。

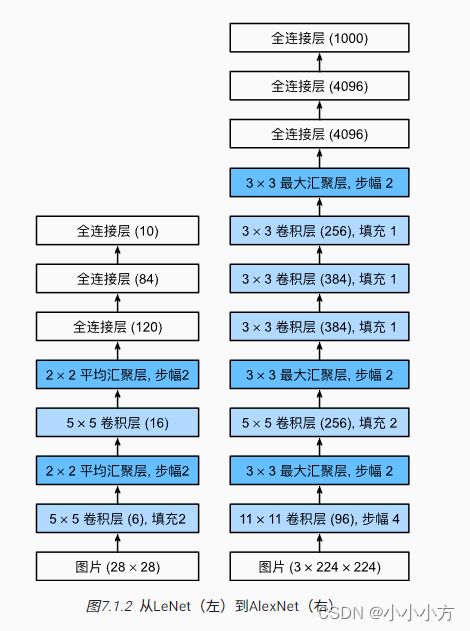
AlexNet由八层组成，五个卷积层、两个全连接层和一个全连接输出层，使用ReLU作为激活函数，使用不同的参数初始化方法，ReLU激活函数使训练模型更加容–sigmoid函数的输出非常接近0时，这些区域的梯度几乎为0，会影响反向传播继续更新模型参数。使用暂退法（dropout=0.5）来控制全连接层的模型复杂度，为了进一步扩充数据，在训练时候增加了大量的图像增强数据，使得模型更加健壮，更大的样本量有效的减少过拟合。使用更大的卷积核，因为图片的输入更大了，同时输出的通道数也增加，希望在第一层的时候就能学到更多的特征。

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
      nn.Conv2d(1,96,kernel_size = 11,stride=4,padding=1),
      nn.ReLU(),
      nn.MaxPool2d(kernel_size=3,stride=2),
      nn.Conv2d(96,256,kernel_size=5,padding=2),
      nn.ReLU(),
      nn.MaxPool2d(kernel_size=3,stride=2),
      nn.Conv2d(256,384,kernel_size=3,padding=1),
      nn.ReLU(),
      nn.Conv2d(384,384,kernel_size=3,padding=1),
      nn.ReLU(),
      nn.Conv2d(384,256,kernel_size=3,padding=1),
      nn.ReLU(),
      nn.MaxPool2d(kernel_size=3,stride=2),
      nn.Flatten(),
      nn.Linear(6400,4096),nn.ReLU(),nn.Dropout(p=0.5),
      nn.Linear(4096,4096),nn.ReLU(),nn.Dropout(p=0.5),
      nn.Linear(4096,10))
# 构造一个单通道数据 来观察每一层的输出的形状
X= torch.randn(1,1,224,224)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)
运行结果：
Conv2d output shape:	 torch.Size([1, 96, 54, 54])
ReLU output shape:	 torch.Size([1, 96, 54, 54])
MaxPool2d output shape:	 torch.Size([1, 96, 26, 26])
Conv2d output shape:	 torch.Size([1, 256, 26, 26])
ReLU output shape:	 torch.Size([1, 256, 26, 26])
MaxPool2d output shape:	 torch.Size([1, 256, 12, 12])
Conv2d output shape:	 torch.Size([1, 384, 12, 12])
ReLU output shape:	 torch.Size([1, 384, 12, 12])
Conv2d output shape:	 torch.Size([1, 384, 12, 12])
ReLU output shape:	 torch.Size([1, 384, 12, 12])
Conv2d output shape:	 torch.Size([1, 256, 12, 12])
ReLU output shape:	 torch.Size([1, 256, 12, 12])
MaxPool2d output shape:	 torch.Size([1, 256, 5, 5])
Flatten output shape:	 torch.Size([1, 6400])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 10])

# Fashion-MNIST图像的分辨率低于ImageNet图像，我们将他增加到224*224
batch_size = 128
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size,resize=224)
#训练AlexNet 学习率的下降会增加训练的时间
lr,num_epochs = 0.01,10
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())
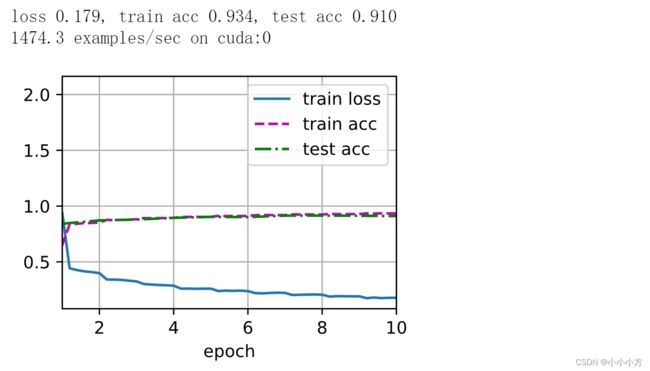
运行结果:

1.使用更多的卷积层和更多的参数来拟合大规模的数据集
2.Dropout（正则项）、ReLU和预处理是提升计算机视觉任务性能的关键
3.使用了数据增强（随机截取，调整图片的亮度色温等）
4.ALexNet比LeNet学习的参数更多,机器找到的特征是不符合人类逻辑的。论文中提及的LRN是正则化技术，但是用处不大。因为前面的卷积特征抽取的不够深刻，所以需要两个dense来进行补充。

使用块的网络VGG

AlexNet没有提供一个通用的模板来指导后续的研究人员设计新的网络，结构不够清晰，研究人员开始从单个神经元的角度思考问题，发展到整个层，现在又转向块，重复层的模式。
思考怎样才能获得更深和更大的网络？更多的全连接层？更多的卷积层？将卷积层组合成块？
经典的卷积神经网络的基本组成部分：
1.带填充以保持分辨率的卷积层 2.非线性激活层 3.汇聚层
VGG块由一系列的卷积层组成，后面再加上用于空间下采样的最大池化层。使用了带有33卷积核，填充为1的卷积层，和带有22窗口，步幅为2的最大池化层。

VGG神经网络连接几个VGG块，其中有超参数变量conv_arch。该变量指定了每个VGG块里卷积层个数和输出通道数。全连接模块则与AlexNet中的相同。原始VGG网络有5个卷积块，其中前两个块各有一个卷积层，后三个块各包含两个卷积层。第一个模块有64个输出通道，每个后续模块将输出通道数量翻倍，直到该数字达到512。由于该网络使用8个卷积层和3个全连接层，被称为VGG-11。
VGG-11使用可复用的卷积块构造网络。不同的VGG模型可以通过每个块中卷积层的数量和输出通道数量的差异来定义。块的使用导致网络定义的非常简洁，使用块可以有效的设计更复杂的网络。在VGG论文中，发现深层且窄的卷积比较浅层且宽的卷积更有效。

import torch
from torch import nn
from d2l import torch as d2l

# 参数：重复的卷积层的个数，输出的通道数，输入的通道数
def vgg_block(num_convs,in_channels,out_channels):
    layers =[]
    for _ in range(num_convs):
        layers.append(nn.Conv2d(
        in_channels,out_channels,kernel_size=3,padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    # 放入sequential中变成一个vgg的块
    return nn.Sequential(*layers)

#VGG网络
# 每块会做最大池化，输入尺寸减半
conv_arch = ((1,64),(1,128),(2,256),(2,512),(2,512))
def vgg(conv_arch):
    conv_blks=[]
    in_channels=1
    for (num_convs,out_channels) in conv_arch:
        conv_blks.append(vgg_block(
        num_convs,in_channels,out_channels))
        in_channels = out_channels
        
    return nn.Sequential(
    *conv_blks,nn.Flatten(),
    nn.Linear(out_channels*7*7,4096),nn.ReLU(),
    nn.Dropout(0.5),nn.Linear(4096,4096),nn.ReLU(),
    nn.Dropout(0.5),nn.Linear(4096,10))
net = vgg(conv_arch)
# 观察每一层的输出形状
X = torch.randn(size=(1,1,224,224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__,'output shape:\t',X.shape)

Sequential output shape:	 torch.Size([1, 64, 112, 112])
Sequential output shape:	 torch.Size([1, 128, 56, 56])
Sequential output shape:	 torch.Size([1, 256, 28, 28])
Sequential output shape:	 torch.Size([1, 512, 14, 14])
Sequential output shape:	 torch.Size([1, 512, 7, 7])
Flatten output shape:	 torch.Size([1, 25088])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 10])


# 由于VGG-11比AlexNet计算量更大，构建了一个通道数较少的网络 将所有的通道数除以4
ratio = 4
small_conv_arch =[(pair[0],pair[1]//ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

# 观察每一层的输出形状2：
Y = torch.randn(size=(1,1,224,224))
for blk in net:
    Y = blk(Y)
    print(blk.__class__.__name__,'output shape:\t',Y.shape)

运行结果：
Sequential output shape:	 torch.Size([1, 16, 112, 112])
Sequential output shape:	 torch.Size([1, 32, 56, 56])
Sequential output shape:	 torch.Size([1, 64, 28, 28])
Sequential output shape:	 torch.Size([1, 128, 14, 14])
Sequential output shape:	 torch.Size([1, 128, 7, 7])
Flatten output shape:	 torch.Size([1, 6272])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 4096])
ReLU output shape:	 torch.Size([1, 4096])
Dropout output shape:	 torch.Size([1, 4096])
Linear output shape:	 torch.Size([1, 10])


# 训练模型
lr,num_epochs,batch_size = 0.05,10,128
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size,resize=224)
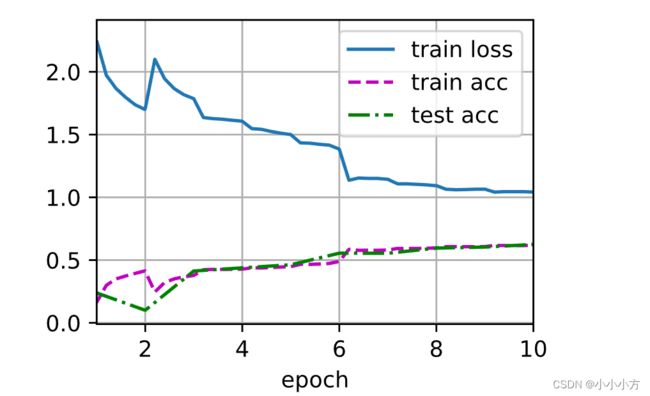
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())

使用网络中的网络

全连接层会特别占据参数的空间，更加容易过拟合

LeNet、AlexNet和VGG都有一个共同的设计模式：通过一系列的卷积层和汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。使用全连接层可能会完全放弃表征的空间结构。网络中的网络提供了一个非常简单的解决方案：在每个像素的通道上分别使用多层感知机。
11的卷积层可以等价为一个全连接层，步幅为1，无填充，输出形状跟卷积层输出一样，起到全连接层的作用。

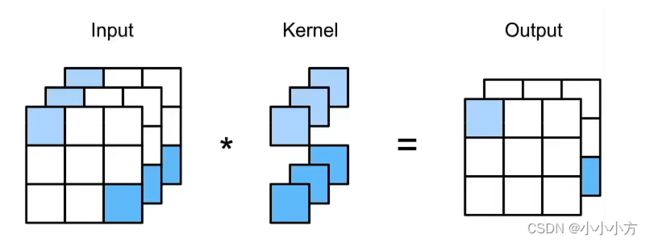
卷积层的输入和输出由四维张量组成，张量的每个轴分别对应样本、通道、高度和宽度。全连接层的输入和输出分别对应于样本和特征的二维张量。NiN的想法是在每个像素位置应用一个全连接层。如果将权重连接到每个位置空间，可以视为11的卷积层，或作为在每个像素位置上独立作用的全连接层，将空间维度中的每个像素视为单个样本，将通道维度视为不同的特征。

NiN块以一个普通的卷积层开始，后面是两个1*1 的卷积层，这两个卷积层充当带有Re
LU的激活函数的逐像素全连接层。第一层卷积窗口的形状通常都是由用户设置的。每个NiN块之后有一个最大汇聚层。NiN块中输出通道数等于标签类别的数量。最后一个全局平均汇聚层，生成一个对数几率，显著减少了模型所需参数的数量，但是会增加模型训练的时间。

import torch
from torch import nn
from d2l import torch as d2l
# 输入的通道数和输出的通道数 第一个卷积层的大小 步幅和padding
def nin_block(in_channels,out_channels,kernel_size,strides,padding):
    return nn.Sequential(
    nn.Conv2d(in_channels,out_channels,kernel_size,strides,padding),
    nn.ReLU(),nn.Conv2d(out_channels,out_channels,kernel_size=1),
    nn.ReLU(),nn.Conv2d(out_channels,out_channels,kernel_size=1),
    nn.ReLU())

#NiN模型
net =nn.Sequential(
    nin_block(1,96,kernel_size =11,strides=4,padding=0),
    nn.MaxPool2d(3,stride=2),
    nin_block(96,256,kernel_size = 5,strides=1,padding=2),
    nn.MaxPool2d(3,stride=2),
    nin_block(256,384,kernel_size = 3,strides=1,padding=1),
    nn.MaxPool2d(3,stride=2),
    nin_block(384,10,kernel_size = 3,strides=1,padding=1),
    # 全局的平均池化层 输出是一个4D
    nn.AdaptiveAvgPool2d((1,1)),
    nn.Flatten()  
     )
# 查看每个块的输出形状
X = torch.rand(size=(1,1,224,224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,"output shape",X.shape)

运行结果
Sequential output shape torch.Size([1, 96, 54, 54])
MaxPool2d output shape torch.Size([1, 96, 26, 26])
Sequential output shape torch.Size([1, 256, 26, 26])
MaxPool2d output shape torch.Size([1, 256, 12, 12])
Sequential output shape torch.Size([1, 384, 12, 12])
MaxPool2d output shape torch.Size([1, 384, 5, 5])
Sequential output shape torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape torch.Size([1, 10, 1, 1])
Flatten output shape torch.Size([1, 10])


# 训练模型
lr,num_epochs,batch_size =0.1,10,128
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size,resize=224)
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())

1.N使用由一个卷积层和多个1*1卷积层组成的块。该块可以在卷积神经网络中使用，以允许更多的每像素非线性。
2.NiN去除了容易造成过拟合的全连接层，将它们替换为全局平均池化代替VGG和AlexNet中全连接层（即在所有位置上进行求和），池化层通道数量为所需的输出数量。
3.交替使用NiN块和步幅为2的最大池化层，逐步减小高宽和增大通道数
4.最后使用全局平均池化层得到输出，其输入通道数是类别数。
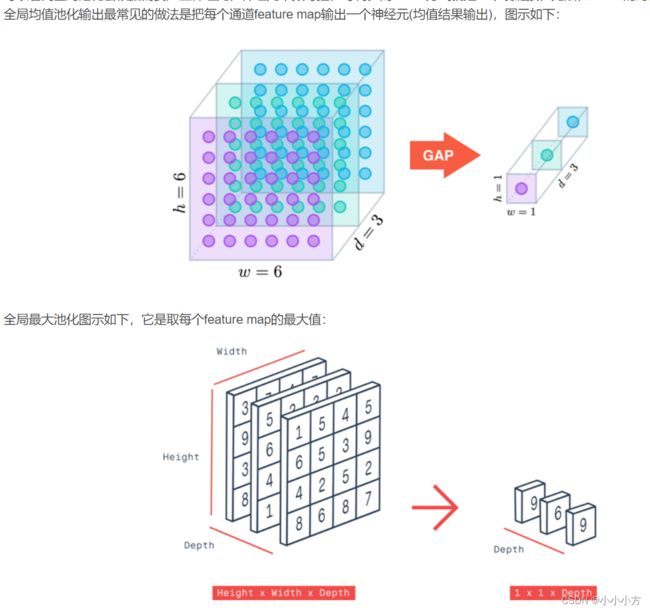
5.卷积后添加全局池化层，将输出特征的宽和高压缩为1，进一步降低模型的复杂度，提高泛化性能，但是收敛变慢。

含并行连接的网络GooleNet

有时使用不同大小的卷积核组合是有利的
现在的GooleNet省略了一些为稳定训练而添加的特殊性质。
GooleNet中基本的卷积块被称为是Inception块,这四条路径使用合适的填充来使得输入与输出的高和宽一致，最后我们将每条路线的输出在通道维度上连结，通常调整的超参数是每层的输出通道数。 第二条和第三条路径首先使用11的卷积层来降低通道数，再放入33的卷积层来降低运算的复杂度。

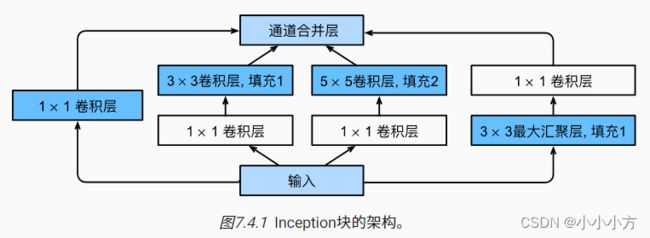
GooleNet使用9个Inception块和全局平均池化层来生成估计值，Inception之间的最大汇聚层可以降低维度。全局池化层避免了在最后使用全连接层

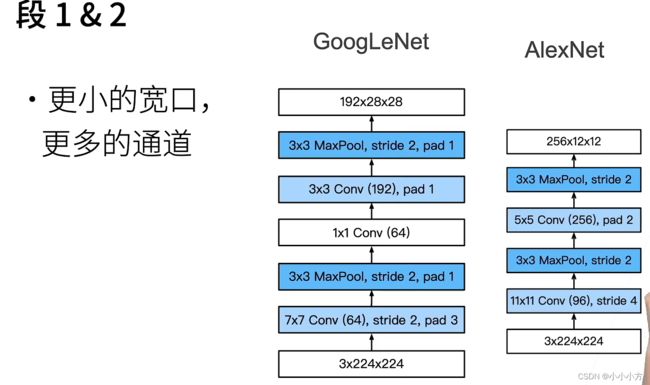
每个stage相当于一个vgg,stage高宽减半。

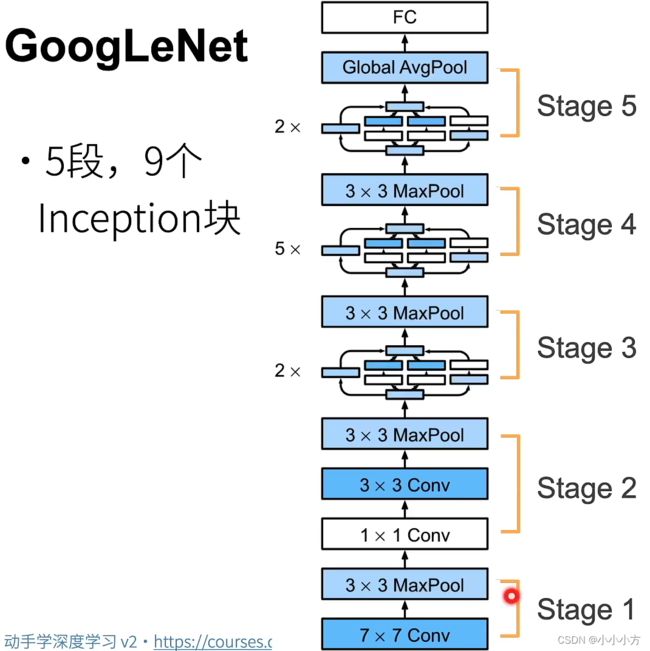
Inception不改变高宽，只改变通道数。


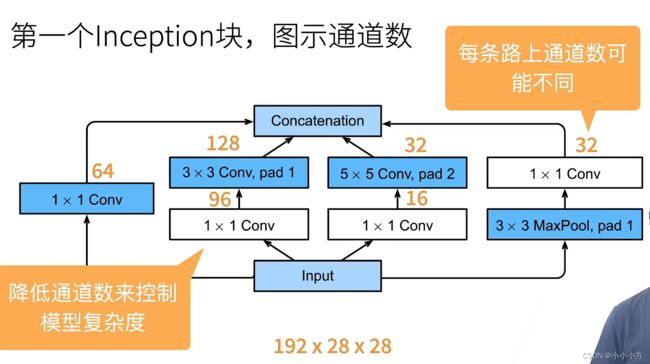
第一个Inception的输出通道数为64+128+32+32=256，第二个Inception的输出通道数为128+192+96+64=480

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self,in_channels,c1,c2,c3,c4,**kwargs):
        super(Inception,self).__init__(**kwargs)
        # 路线1 单1*1卷积层
        self.p1_1 = nn.Conv2d(in_channels,c1,kernel_size=1)
        # 路线2 1*1 卷积层后接3*3卷积层
        self.p2_1 = nn.Conv2d(in_channels,c2[0],kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0],c2[1],kernel_size=3,padding=1)
        #线路3 1*1卷积层后接5*5的卷积层
        self.p3_1 = nn.Conv2d(in_channels,c3[0],kernel_size = 1)
        self.p3_2 = nn.Conv2d(c3[0],c3[1],kernel_size=5,padding=2)
        #线路4 3*3最大汇聚层后接1*1的卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3,stride=1,padding=1)
        self.p4_2 = nn.Conv2d(in_channels,c4,kernel_size=1)
        
    def forward(self,x):
        p1= F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出  按列进行张量之间的拼接
        return torch.cat((p1,p2,p3,p4),dim=1)
# 逐一实现GooleNet每个模块  第一个模块使用64个通道、7*7卷积层
b1 = nn.Sequential(nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
                  nn.ReLU(),
                  nn.MaxPool2d(kernel_size=3,stride=2,padding=1))
# 第二个模块使用两个卷积层：第一个卷积层是64个通道、卷积层；
# 第二个卷积层使用将通道数量增加三倍的卷积层。
# 这对应于Inception块中的第二条路径
b2 =nn.Sequential(nn.Conv2d(64,64,kernel_size=1),
                 nn.ReLU(),
                 nn.Conv2d(64,192,kernel_size=3,padding=1),
                 nn.ReLU(),
                 nn.MaxPool2d(kernel_size=3,stride=2,padding=1))
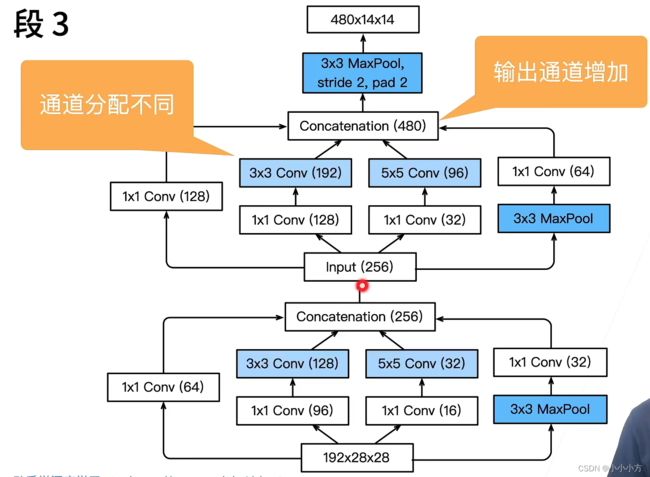
# 第三个模块串联两个完整的Inception块
# 第一个Inception块的输出通道数为64+128+32+32=256
# 第二个Inception块的输出通道数增加到128+192+96+64=480
b3 = nn.Sequential(Inception(192,64,(96,128),(16,32),32),
                  Inception(256,128,(128,192),(32,96),64),
                  nn.MaxPool2d(kernel_size=3,stride=2,padding=1))
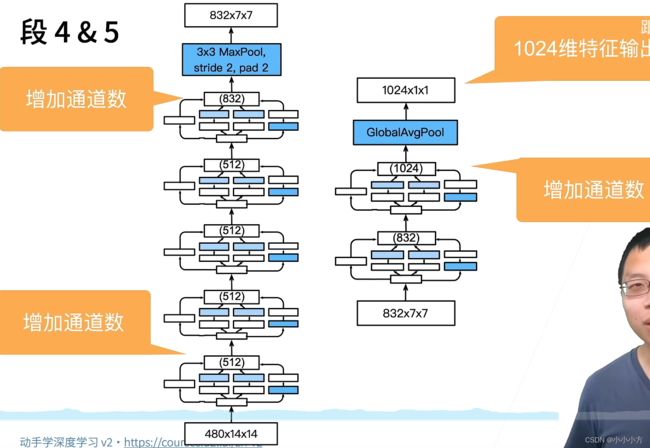
#第四个模块，串联了5个Inception，输出通道数是192+208+48+64=512
# 160+224+64+64=512、128+256+64+64=512、112+288+64+64=528、256+320+128+128=832
# 这些路径的通道数分配类似，第二条和第三条路径会按比例减少通道数
b4 = nn.Sequential(Inception(480,192,(96,208),(16,48),64),
                   Inception(512,160,(112,224),(24,64),64),
                   Inception(512,128,(128,256),(24,64),64),
                   Inception(512,112,(144,288),(32,64),64),
                   Inception(528,256,(160,320),(32,128),128),
                   nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

# 第五模块的输出通道数为256+320+128+128=832和384+384+128+128=1024
# 每个通道的分配思路和之前的类似
# 第五个模块之后紧跟着输出层，该模块通NiN一样使用全局平均池化层，将每个通道的高和宽变成1
# 最后将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层
b5 = nn.Sequential(Inception(832,256,(160,320),(32,128),128),
                  Inception(832,384,(192,384),(48,128),128),
                  nn.AdaptiveAvgPool2d((1,1)),
                  nn.Flatten())
net = nn.Sequential(b1,b2,b3,b4,b5,nn.Linear(1024, ))        

# GooleNet计算复杂，将输入的高宽降到96
X = torch.rand(size=(1,1,96,96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape',X.shape)           
Sequential output shape torch.Size([1, 64, 24, 24])
Sequential output shape torch.Size([1, 192, 12, 12])
Sequential output shape torch.Size([1, 480, 6, 6])
Sequential output shape torch.Size([1, 832, 3, 3])
Sequential output shape torch.Size([1, 1024])
Linear output shape torch.Size([1, 10])

# 训练模型
lr,num_epochs,batch_size = 0.1,10,128
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size,resize=96)
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())

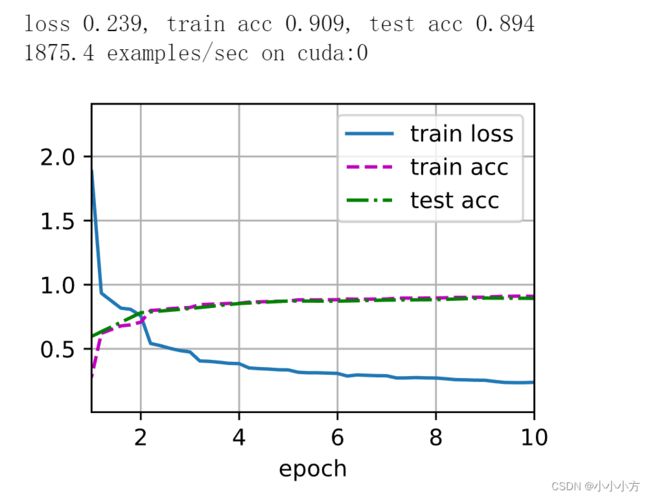
Inception有各种后续的变种：




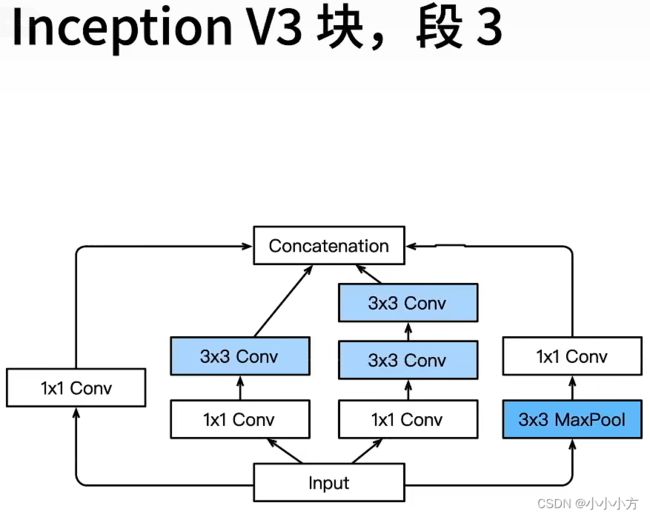
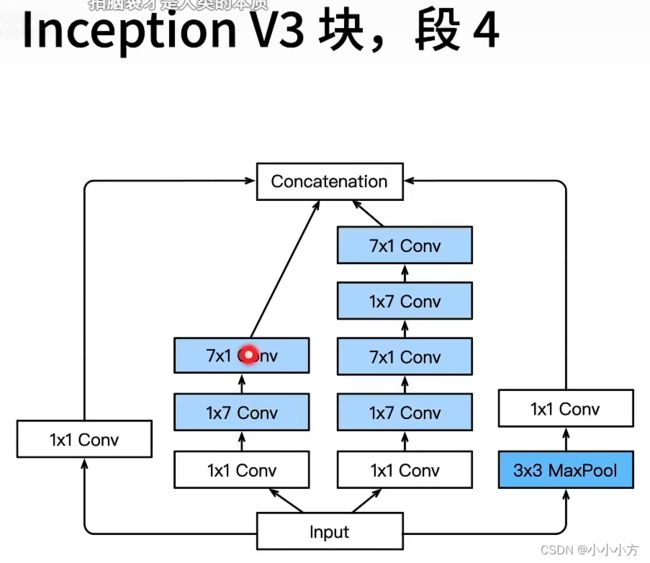
1.Inception块用4条不有不同超参数的卷积层和池化层的路来抽取不同的信息
2.模型参数小，计算复杂度高
3.是第一个达到上百层的网络，后续也有一系列的改进

批量规范化

课程评论区根据课程做的笔记，十分详细：链接: link
对深度的神经网路会好一些
梯度的值会更大些，可以使用更大的学习率。对权重的更新会变快

import torch
from torch import nn
from d2l import torch as d2l

# 定义数学原理
# moving_mean,moving_var整个数据集的均值和方差 momentum用来更新均值和方差通常为标量
def batch_normal(X,gamma,beta,moving_mean,moving_var,eps,momentum):
    #判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 预测模式直接使用传入的移动平均所得的均值和方差
        X_hat = (X-moving_mean)/torch.sqrt(moving_var+eps)
    else:
        assert len(X.shape) in(2,4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差 方差和均值都是行向量
            mean = X.mean(dim=0)
            var = ((X -mean)**2).mean(dim=0)
        else:
            # 使用二维卷积的情况，计算通道维（axis=1）的均值和方差 1*n*1*1的4D
            # 保持X的形状以后进行广播计算
            mean = X.mean(dim=(0,2,3),keepdim=True)
            var = ((X-mean)**2).mean(dim=(0,2,3),keepdim=True)
        # 训练模式下，使用当前（小批量中）的均值和方差做标准化
        X_hat =(X-mean)/torch.sqrt(var+eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum*moving_mean+(1.0-momentum)*mean
        moving_var = momentum*moving_var +(1.0-momentum)*var
    Y = gamma*X_hat +beta
    return Y,moving_mean.data,moving_var.data
# 创建一个正确的BatchNorm层  这个层保持适当的参数:拉伸gamma和偏移beta 
# 保持均值和方差的移动平均值
class BatchNorm(nn.Module):
    # num_features 全连接的输出数量或卷积层的输出通道数
    # num_dims：2表示完全连接层4表示卷积层
    def __init__(self,num_features,num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1,num_features)
        else:
            shape = (1,num_features,1,1)
        # 参与梯度和迭代的拉伸和偏移参数 分别初始化成1和0
        # gamma拟合方差 beta拟合均值
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)
    def forward(self,X):
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y,self.moving_mean,self.moving_var = batch_normal(
        X,self.gamma,self.beta,self.moving_mean,
        self.moving_var,eps=1e-5,momentum=0.9)
        return Y
 # 将BatchNorm应用于LeNet模型
# 批量规范化是在卷积层或全连接层之后，相应的激活函数之前应用的
net = nn.Sequential(
      nn.Conv2d(1,6,kernel_size=5),BatchNorm(6,num_dims=4),nn.Sigmoid(),
      nn.AvgPool2d(kernel_size=2,stride=2),
      nn.Conv2d(6,16,kernel_size=5),BatchNorm(16,num_dims=4),nn.Sigmoid(),
      nn.AvgPool2d(kernel_size=2,stride=2),nn.Flatten(),
      nn.Linear(16*4*4,120),BatchNorm(120,num_dims=2),nn.Sigmoid(),
      nn.Linear(120,84),BatchNorm(84,num_dims=2),nn.Sigmoid(),
      nn.Linear(84,10))  
# 使用大学习率来训练LeNet
lr,num_epochs,batch_size=1.0,10,256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())
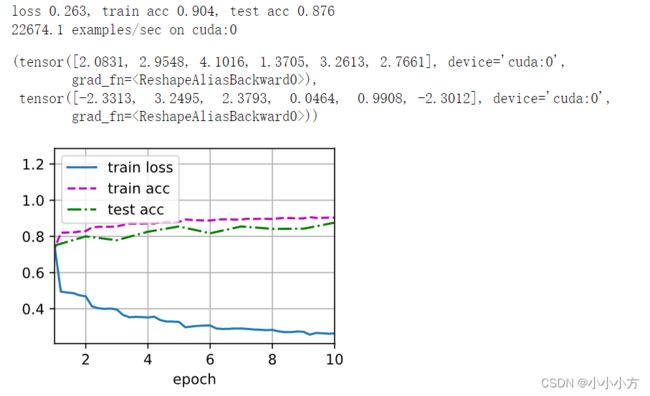
net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))    

运行结果： 

# 使用深度学习框架中定义的BatchNorm
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

数据集不是很稳定，多训练几次，精度会有变化。

残差网络ResNet

随着设计越来越深的网络，新增添的层如何提升神经网络的性能变得至关重要。
残差网络的核心思想是：每个附加层都应该更容易的包含原始函数作为其元素之一。
更复杂的模型不一定能够带来好处

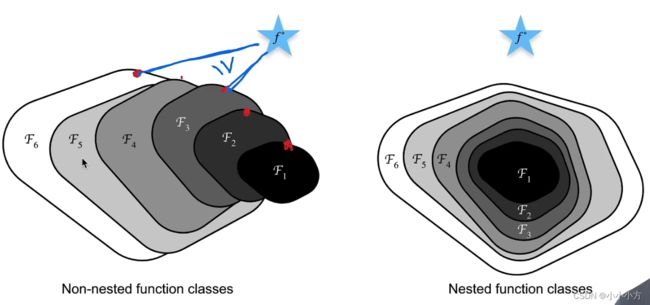
左：可能越深的网络反倒距离最优点越远。右：resnet是增加深度的同时，使得这个模型不会变得更差。

串联一层改变函数类，希望能够扩大函数类，残差块加入快速通道来得的f(x)=x+g(x)的结构。



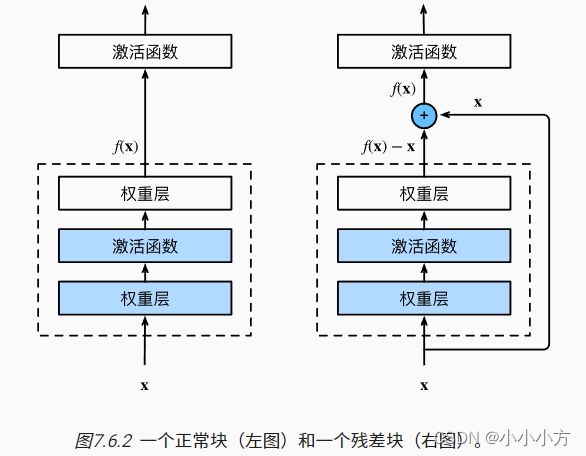
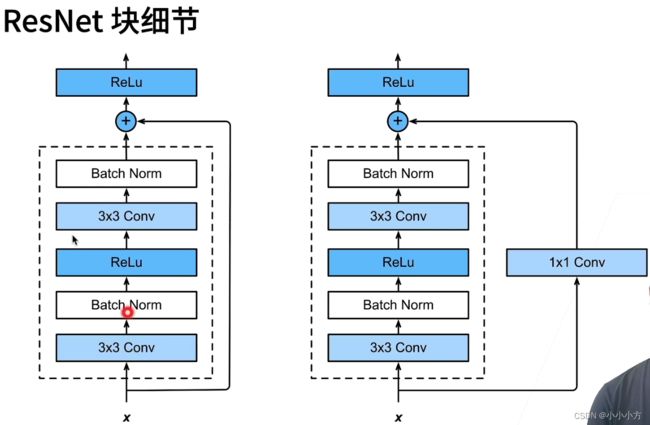
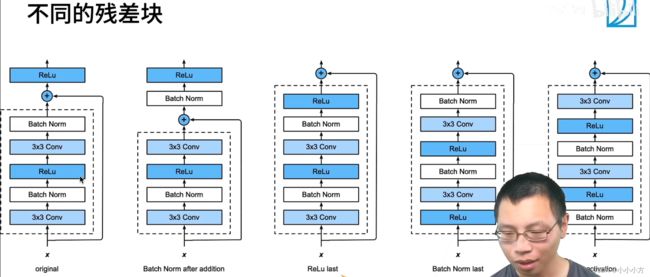
resnet:
高宽减半的ResNet块（步幅为2）后接多个高宽不变的ResNet块。残差块是得很深的网络更加容易训练。

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

# 残差设计
class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

# 输入和输出形状一致
blk = Residual(3,3)
X = torch.rand(4,3,6,6)
Y = blk(X)
Y.shape

torch.Size([4, 3, 6, 6])

# 增加输出通道数的同时，减半输出的高和宽
blk = Residual(3,6,use_1x1conv=True,strides=2)
blk(X).shape

torch.Size([4, 6, 3, 3])

#ResNet模型
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
# 多少个残差块
def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        # 第一个残差块高宽减半
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        # 之后的残差块保持不变
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape:	 torch.Size([1, 64, 56, 56])
Sequential output shape:	 torch.Size([1, 64, 56, 56])
Sequential output shape:	 torch.Size([1, 128, 28, 28])
Sequential output shape:	 torch.Size([1, 256, 14, 14])
Sequential output shape:	 torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape:	 torch.Size([1, 512, 1, 1])
Flatten output shape:	 torch.Size([1, 512])
Linear output shape:	 torch.Size([1, 10])


# 训练模型
lr,num_epochs,batch_size = 0.05,10,256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size,resize=96)
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())

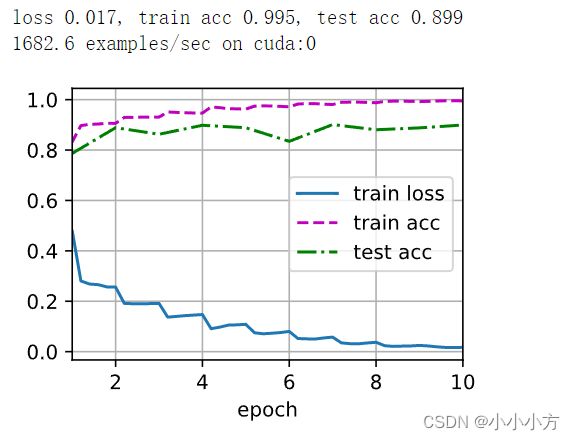
ResNet是怎么处理梯度消失的？
简单理解是：小数*小数还是小数，但是大数+小数还是大数，尽管梯度下降存在小数，但是存在另一个分支的大数，所以可以通过加法来缓解梯度消失问题。

稠密连接DenseNet

ResNet和DenseNet的关键区别在于：DesNe的输出是连接，而不是ResNet的简单相加。ResNet将f分解为两个不服：一个简单的线性项和一个复杂的非线性项，DenseNet将F分解成超过两部分的信息。

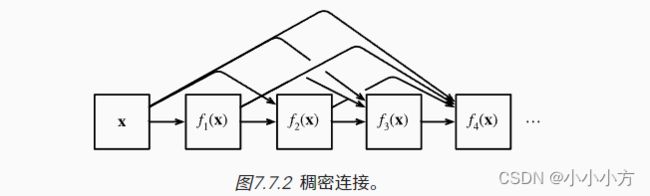
稠密网路主要由两部分构成：稠密块和过渡层。前者定义如何连接输入和输出，后者则控制通道数量，使其不会变得太复杂。

import torch
from torch import nn
from d2l import torch as d2l

def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))

class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X
# 我们定义一个有2个输出通道数为10的DenseBlock。 使用通道数为3的输入时，我们会得到通道数为# 的输出。 卷积块的通道数控制了输出通道数相对于输入通道数的增长，因此也被称为增长率
#（growth rate）。
blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape

torch.Size([4, 23, 8, 8])
# 过渡层
def tranistion_block(input_channels,num_channels):
    return nn.Sequential(
    nn.BatchNorm2d(input_channels),nn.ReLU(),
    nn.Conv2d(input_channels,num_channels,kernel_size=1),
    nn.AvgPool2d(kernel_size=2,stride=2))
# 每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型，过渡层可以用来控制模型复杂度
# 通过1x1卷积层来减小通道数，并使用步幅为2的平均汇聚层减半高和宽，从而进一步的减低模型复杂
# 度
blk = tranistion_block(23,10)
blk(Y).shape

torch.Size([4, 10, 4, 4])


# 构造DenseNet模型，首先使用通ResNet一样的单卷积层和最大汇聚层
b1 = nn.Sequential(
nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
nn.BatchNorm2d(64),nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

# 使用4个稠密块，设置每个块4个卷积层，稠密块里的卷积层通道数设为32，每个稠密块将增加128个
# 通道数
# 在每个模块之间，DenseNet使用过渡层来减半高和宽，并减半通道数
# num_channels为当前的通道数
num_channels,growth_rate = 64,32
num_convs_in_dense_blocks = [4,4,4,4]
blks =[]
for i,num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs,num_channels,growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs*growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) -1:
        blks.append(tranistion_block(num_channels,num_channels//2))
        num_channels = num_channels //2
# 使用全局汇聚层和全连接层来输出结果
net = nn.Sequential(
b1,*blks,
nn.BatchNorm2d(num_channels),nn.ReLU(),
nn.AdaptiveAvgPool2d((1,1)),
    nn.Flatten(),
    nn.Linear(num_channels,10)
)

# 使用较深的网络 输入变成96*96 存在一定的过拟合现象
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())