第一章 图像处理
1.1 PIL:python 图像处理类库
PIL(python Image Library) 提供了通用的图像处理功能,以及大量有用的基本图像操作,比如图像缩放,裁剪,旋转,颜色转换等。PIL可以通过 pip install pillow 下载。利用PIL中的函数,我们可以从大多数图像格式的文件中读取数据,然后写入最常见的图像文件格式中。PIL中最重要的模块为Image。要读取一幅图像,可以使用:
from PIL import Image
pil_im = Image.open('building.jpg')图像的颜色转换可以使用convert()方法来实现。要读取图像,并将其转换成灰度图像,只需要加上convert('L'),如下所示:
pil_im = Image.open('building.jpg').convert('L')效果图:
1.1.1 转换图像格式
通过save()方法,PIL可以将图像保存成多种格式的文件。下面的例子从文件名列表(filelist)中读取所有的图像文件,并转换成.png格式:
from PCV.tools.imtools import get_imlist
from PIL import Image
import os
import pickle
filelist = get_imlist('data/convert_images_format_test') # 获取convert_images_format_test文件夹下的图片文件名
imlist = open('data/convert_images_format_test/imlist.txt', 'wb')
pickle.dump(filelist, imlist) # 序列化
imlist.close()
for infile in filelist:
outfile = os.path.splitext(infile)[0] + ".png" # 分离文件名和扩展名
if infile != outfile:
try:
Image.open(infile).save(outfile)
except IOError:
print("Cannot convert", infile)PIL的open()函数用于创建PIL图像对象,save()方法用于保存图像到具有指定文件名的文件,除了后缀变为".jpg",上述代码的新文件名和原文件名相同。PIL是足够智能的类库,可以根据文件扩展名来判断图像的格式。PIL函数会进行简单的检查, 如果文件不是png格式,会自动将其转化成png格式,如果转化失败,它会在控制台输出一条报告失败的消息。
1.1.2 创建缩略图
使用PIL可以很方便的创建图像的略缩图。thumbnail()方法接受一个元组参数,然后将图像转换成符和元组参数指定大小的略缩图。例如,创建最长边为128像素的略缩图,可以使用如下命令:
pil_im.thumbnail((128, 128))
1.1.3 复制粘贴图像区域
使用crop()方法可以从一幅图像中裁剪指定区域:
box = (100, 100, 1000, 1000)
region = pil_im.crop(box)该区域使用四元组来指定。四元组坐标依次是(左,上,右,下)。PIL中指定坐标系的左上角坐标为(0,0)。我们可以旋转上面代码中获取的区域,然后使用paste()方法将该区域放回去,具体实现如下:
region = region.transpose(Image.ROTATE_180)
pil_im.paste(region, box)1.1.4 调整尺寸和旋转
要调整一幅图像的尺寸,我们可以使用resize()方法。该方法的参数是一个元组,用来指定新图像的大小:
pil_im = pil_im.resize((128, 128))要旋转一幅图像,可以使用逆时针方式表示旋转角度,然后调用rotate()方法:
pil_im = pil_im.rotate(45)整理得:
from PIL import Image
from pylab import *
# 添加中文字体支持
'''
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
figure()
'''
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
# 显示原图
pil_im = Image.open('building.jpg')
subplot(231)
title(u'原图')
axis('off')
imshow(pil_im)
# 显示灰度图
pil_im = Image.open('building.jpg').convert('L')
gray()
subplot(232)
title(u'灰度图')
axis('off')
imshow(pil_im)
# 拷贝粘贴区域
pil_im = Image.open('building.jpg')
box = (100, 100, 1000, 1000)
region = pil_im.crop(box)
region = region.transpose(Image.ROTATE_180)
pil_im.paste(region, box)
subplot(233)
title(u"拷贝粘贴区域")
axis('off')
imshow(pil_im)
# 缩略图
pil_im = Image.open("building.jpg")
size = 128, 128
pil_im.thumbnail(size)
print(pil_im.size)
subplot(234)
title(u'缩略图')
axis('off')
imshow(pil_im)
pil_im.save('thumbnail.jpg')
# 调整图像尺寸
pil_im = Image.open('building.jpg')
pil_im = pil_im.resize(size)
print(pil_im.size)
subplot(235)
title(u'调整尺寸后的图像')
axis('off')
imshow(pil_im)
# 旋转图像45°
pil_im = Image.open('building.jpg')
pil_im = pil_im.rotate(45)
subplot(236)
title(u'旋转45°后的图像')
axis('off')
imshow(pil_im)
show()效果图:
1.2 Matplotlib
我们处理数学运算,绘制图表,或者在图像上绘制点,直线,和曲线时,matplotlib是个很好的类型库,具有比PIL更强大的绘图功能。matplotlib可以绘制出高质量的图表。
1.2.1 绘制图像、点和线
尽管matplotlib可以绘制出比较好的条形图,饼状图,散点图等,但是对于大多数计算机视觉应用来说,仅仅需要用到几个绘图命令。最重要的是,我们想用点和线条表示一些事物,比如兴趣点,对应点以及检测出的物体。下面是用几个点和一条线绘制图像的例子:
from PIL import Image
from pylab import *
im = array(Image.open('building2.jpg'))
imshow(im)
效果图:
# x, y 的设置与标点有关
x = [100, 100, 400, 400]
y = [200, 500, 200, 500]
plot(x, y, 'r*') # 标点,‘r*’设置颜色
plot(x[:2], y[:2]) # 与画线有关
title(u'绘图:“building.jpg”')效果图:
上面的代码首先绘制出原始图像,然后在x和y列表中给定点的x坐标和y坐标上绘制出红色星状标记,最后在两个列表表示的前两个点之间绘制一条线段。
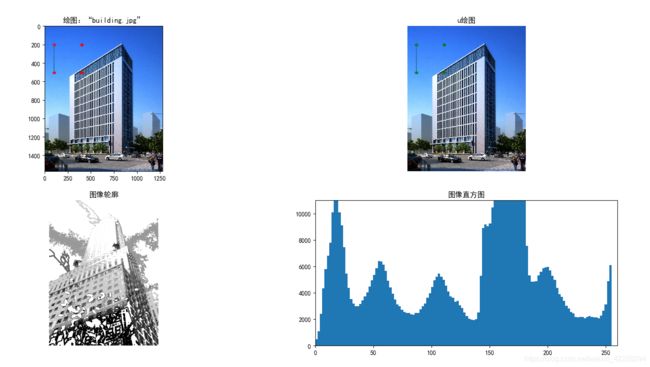
1.2.2 图像轮廓和直方图
下面来看两个特别的绘图示例:图像的轮廓和直方图。绘制图像的轮廓在工作中非常有用。因为绘制轮廓需要对每个坐标[x,y] 的像素值施加同一个阙值,所以首先需要将图像灰度化,像之前的例子一样,这里用PIL的convert()方法将图像转化为灰度图像。图像的直方图用来表征该图像像素值分布情况。用一定数目的小区间来指定表征像素值的范围,每个小区间会得到落入该小区间表示范围的像素数目。hist()函数的第二个参数指定小区间的数目。值得注意的是,因为hist() 只接受一维数组作为输入,所以我们在绘制图像直方图之前,必须对图像进行压平处理。flatten()方法将任意数组按照有限准则转换为一维数组。
代码整理如下:
from PIL import Image
from pylab import *
import matplotlib.pyplot as plt
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
im = array(Image.open('building.jpg'))
figure()
# 画有坐标轴的
subplot(221)
imshow(im)
# x, y 的设置与标点有关
x = [100, 100, 400, 400]
y = [200, 500, 200, 500]
plot(x, y, 'r*') # 标点,‘r*’设置颜色
plot(x[:2], y[:2]) # 与画线有关
title(u'绘图:“building.jpg”')
# 不显示坐标轴
subplot(222)
imshow(im)
x = [100, 100, 400, 400]
y = [200, 500, 200, 500]
plot(x, y, 'g*')
plot(x[:2], y[:2])
axis('off')
title('u绘图')
# 显示图像轮廓
subplot(223)
gray()
img = array(Image.open('building2.jpg').convert('L'))
contour(img, origin='image')
axis('equal')
axis('off')
title(u'图像轮廓')
subplot(224)
hist(img.flatten(), 128)
title(u'图像直方图')
plt.xlim([0, 260])
plt.ylim([0, 11000])
show()
效果图:
1.2.3 交互式标注
有时用户需要和某些应用交互,例如在一幅图像中标记一些点,或者标注一些训练数据。Pylab库中的ginput()函数就可以实现交互式标注,下面是一个简短的例子:
from PIL import Image
from pylab import *
im = array(Image.open('building2.jpg')) # 图像数组表示
imshow(im)
print('Please click 3 points')
imshow(im)
x = ginput(3) # 点击3下会显示点击位置得坐标
print('You clicked:', x)
show()1.3 Numpy
Numpy 是非常有名的Python科学计算工具包,其中包含了大量有用的思想,比如数组对象(用来表示向量,矩阵,图像等)以及线性代数函数。Numpy的数组对象可以帮你实现数组中重要的操作,比如矩阵乘积,转置,解方程系统,向量乘积和归一化,这为图像变形,对图像进行建模,图像分类,图像聚类提供了基础。
1.3.1 图像数组表示
在先前的例子中,当载入图像时,我们通过调用array()方法将图像转换成Numpy的数组对象。Numpy中的数组对象是多维的,可以用来表示向量,矩阵和图像。一个数组对象很像一个列表,但是数组中所有的元素必须具有相同的数据类型。除非创建数组对象是指定数据类型,否额数据类型会按照数据的类型自动确定。对于图像数据,下面的例子阐述了这一点:
from PIL import Image
from pylab import *
from numpy import *
im = array(Image.open('building2.jpg'))
print(im.shape, im.dtype)
im = array(Image.open('building2.jpg').convert('L'), 'f')
print(im.shape, im.dtype)效果图:
每行的第一个元组表示图像数组的大小(行,列,颜色通道),紧接着的字符串表示数组元素的数据类型。因为图像常常被编码成无符号八位整数,所以在第一种情况下,载入图像并将其转换到数组中,数组的数据类型为‘unit8‘。在第二中情况下,对图像进行灰度化处理,并且在创建数组时使用额外的参数'f'。该参数将数据类型转换为浮点型。多个数据元素可以使用数组切片方式访问。切片方式返回的是以指定间隔下访问该数组的元素值。下面是一些有关灰度值的例子:
im[i,:] = im[j,:] # 将第j行的数值赋值给第i行
im[:,i] = 100 # 将第i列的所有数值设为100
im[:100,:50].sum() # 计算前100行,前50列所有数值的和
im[50:100,50:100] #50-100 行,50-100列
im[i].mean() #第i行所有数值的平均值
im[:,-1] #最后一列
im[-2,:] #倒数第二行1.3.2 灰度变换
将图像读入Numpy数组对象后,我们可以对它执行任意数学操作。一个简单的例子就是图像的灰度变换。考虑任意函数f,它将0....255映射到自身 ,意思就是输出区间和输入区间的范围相同。下面是关于灰度变换的一些例子:
from PIL import Image
from pylab import *
from numpy import *
'''
im = array(Image.open('building2.jpg'))
print(im.shape, im.dtype)
im = array(Image.open('building2.jpg').convert('L'), 'f')
print(im.shape, im.dtype)
'''
im = array(Image.open('building2.jpg').convert('L'))
print(int(im.min()), int(im.max()))
im2 = 255 - im # invert image
print(int(im2.min()), int(im2.max()))
im3 = (100.0/255)*im+100 # clamp to interval 100...200
print(int(im3.min()), int(im3.max()))
im4 = 255.0*(im/255.0)**2 # squared
print(int(im4.min()), int(im4.max()))
figure()
gray()
subplot(1, 3, 1)
imshow(im2)
axis('off')
title(r'$f(x)=255-x$')
subplot(1, 3, 2)
imshow(im3)
axis('off')
title(r'$f(x)=\frac{100}{255}x+100$')
subplot(1, 3, 3)
imshow(im4)
axis('off')
title(r'$f(x)=255(\frac{x}{255})^2$')
show()效果图:
1.3.3 图像缩放
Numpy的数组对象是我们处理图像和数据的主要工具。想要对图像进行缩放处理没有现成简单的方法。我们之所以使用之前的PIL对图像对象转换的操作,写一个简单的用于图像缩放的函数。
def imresize(im, sz):
''' Resize an image array using PIL. '''
pil_im = Image.fromarray(uint8(im))
return array(pil_im.resize(sz))
1.3.4 直方图均衡化
图像灰度变换中一个非常有用的例子就是直方图均衡化。直方图均衡化是指将一幅图像的灰度直方图变平,使变换后的图像中的每个灰度值的分布概率都相同。对图像做进一步处理之前,直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法,而且可以增强图像的对比度。在这种情况下,直方图均衡化的变换函数是图像中像素值的累积分布函数cumulative distribution function简写成cdf,将像素值的范围映射到目标范围的归一化操作。下面的函数是直方图均衡化的具体实现。
def histep(im,nbr_bins=256):
"""对一副灰度图像进行直方图均衡化"""
#计算图像的直方图
imhist,bins = histogram(im.flatten(),nbr_bins,normed=True)
cdf = imhist.cumsum() #累积分布函数
cdf = 255 *cdf/cdf[-1] #归一化
#使用累积分布函数的线性插值,计算新的像素值
im2 = interp(im,flatten(),bins[:-1],cdf)
return im2.reshape(im.shape),cdf该函数有两个输入参数,一个是灰度图像,一个是直方图中使用小区间的数目。函数返回直方图均衡化后的图像,以及用来做像素值映射的累积分布函数。注意,函数中使用到累积分布函数的最后一个元素,目的是将其归一化到0...1。可以像下面一样使用该函数。
# 打开图像并转化成灰度图
im = array(Image.open('building2.jpg').convert('L'))
# 对一幅灰度图进行直方图均衡化
im2, cdf = imtools.histeq(im)
代码整理如下:
from PIL import Image
from pylab import *
from PCV.tools import imtools
# 添加中文支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
# 打开图像并转化成灰度图
im = array(Image.open('building2.jpg').convert('L'))
# 对一幅灰度图进行直方图均衡化
im2, cdf = imtools.histeq(im)
figure()
subplot(2, 2, 1)
axis('off')
gray()
title(u'原始图像')
imshow(im)
subplot(2, 2, 2)
axis('off')
title(u'直方图均衡化后的图像')
imshow(im2)
subplot(2, 2, 3)
axis('off')
title(u'原始直方图')
hist(im.flatten(), 128, normed=True)
subplot(2, 2, 4)
axis('off')
title(u'均衡化的直方图')
hist(im2.flatten(), 128, normed=True)
show()效果图:
1.3.5 图像平均
图像平均操作是减少图像噪声的一种简单方式,通常用于艺术特效。我们可以简单地从图像列表中计算出一副平均图像。假设所有的图像具有相同的大小,我们可以将这些图像简单的相加,然后除以图像的数目,来计算平均图像。下面函数可以计算平均图像。
def compute_average(imlist):
""" Compute the average of a list of images. """
# open first image and make into array of type float
averageim = array(Image.open(imlist[0]), 'f')
skipped = 0
for imname in imlist[1:]:
try:
averageim += array(Image.open(imname))
except:
print (imname + "...skipped" )
skipped += 1
averageim /= (len(imlist) - skipped)
# return average as uint8
return array(averageim, 'uint8')如是对3张图片的平均操作:
from PCV.tools.imtools import get_imlist
from PIL import Image
from pylab import *
from PCV.tools import imtools
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
# 获得文件夹下的文件名
filelist = get_imlist('data/avg/')
avg = imtools.compute_average(filelist)
for impath in filelist:
im1 = array(Image.open(impath))
subplot(2, 2, filelist.index(impath)+1)
imshow(im1)
imNum = str(filelist.index(impath)+1)
title(u'待平均图像'+imNum)
axis('off')
subplot(2, 2, 4)
imshow(avg)
title(u'平均后的图像')
axis('off')
show()
效果图如下:
1.3.6 图像的主成分分析(PCA)
PCA(principal component analysis) 是一个非常有用的降维技巧。它可以在使用尽可能少维数的前提下,尽量多的保持训练数据的信息,在此意义上是一个最佳技巧。即使一副100*100 像素大小的灰度图像,也有10000维,可以看成10000维空间中的一个点。一兆像素的图像具有百万维。由于图像具有很高的维数,在许多计算机视觉应用中,我们经常使用降维操作。PCA产生的投影矩阵可以视为将原始坐标变换到现有的坐标系,坐标系中的各个坐标按照重要性递减排列。为了对图像数据进行PCA变换,图像需要转换为一维向量表示。我们可以使用Numpy类库中的flatten()方法进行变换。将变平的图像堆积起来,我们可以得到一个矩阵,矩阵的一行表示一副图像。在计算主方向之前,所有行图像按照平均图像进行中心化。我们通常使用SVD(singular value decomponent)奇异值分析方法来计算主成分;但当矩阵的维数很大时,SVD的计算非常慢,所以此时通常不使用SVD分解。下面就是PCA操作的代码:
def pca(X):
""" 主成分分析:
输入:矩阵X,其中该矩阵中存储训练数据,每一行为一条训练数据
返回:投影矩阵,按照维度的重要性排序,方差和平均值
"""
#获取维数
num_data,dim= X.shape
#数据中心化
mean_X = X.mean(axis=0)
X = X - mean_X
if dim >num_data:
#pca-使用紧致技巧
M = dot(X,X.T)# 协方差理论
e,EV = linalg.eigh(M) #特征值和特征向量
tmp = dot(X.T,EV).T#这就是紧致技巧
V = tmp[::-1]#由于最后的特征向量是我们所需的,所以需要将其逆转
S = sqrt(e)[::-1]#由于特征值是按照递增顺序排列的,所以需要将其逆转
for i in range(V.shape[1]):
V[:,i] /= S
else:
U,S,V = linalg.svd(X)
V = V[:num_data] #仅仅返回前num_data维数组才合理
return V,S,mean_X # 返回投影矩阵,方差和均值该函数首先通过减去每一维的均值将数据中心化,然后计算协方差矩阵对应最大特征值的特征向量,此时可以使用简明的技巧或者SVD分解。这里我们使用了range()函数,该函数的输入参数为一个整数n,函数返回整数0...(n-1)的一个列表。你也可以使用arrange()函数来返回一个数组,或者使用xrange函数返回一个产生器。
下面代码是对一组头像进行主成分分析:
import pickle
from PIL import Image
from numpy import *
from pylab import *
from PCV.tools import imtools, pca
# 获取图像列表和他们的尺寸
imlist = imtools.get_imlist('data/size100')
im = array(Image.open(imlist[0])) # open one image to get the size
m, n = im.shape[:2] # get the size of the images
imnbr = len(imlist) # get the number of images
print('The number of images is %d' % imnbr)
# Create matrix to store all flattened images (记得转换成灰度图确保矩阵大小的可reshape)
immatrix = array([array(Image.open(imname).convert('L')).flatten() for imname in imlist], 'f')
# PCA降维
v, S, immean = pca.pca(immatrix)
# show the images (mean and 7 first modes)
# This gives figure 1-8 (p15) in the book.
figure()
gray()
subplot(2, 4, 1)
axis('off')
imshow(immean.reshape(m, n))
for i in range(7):
subplot(2, 4, i+2)
imshow(v[i].reshape(m, n))
axis('off')
show()
效果图如下:
1.3.7 使用pickle模块
如果想要保存一些结果或者数据以方便后续使用,python中的pickle模块非常有用。pickle模块可以接受几乎所有的python对象,并且将其转换成字符串表示,该过程叫做封装(pickling)。从字符串表示中重构该对象,成为拆封(unpickling)。这些字符串表示可以方便的存储和传输。
我们来看一个例子。假设想要保存上一节的平均图像和成分,可以这样来完成:
# 使用Pickle保存数据
f = open('data/size100/pca_modes.pkl', 'wb')
pickle.dump(immean, f)
pickle.dump(v, f)
f.close()加载图像则使用load()函数:
# 如果载入.plk数据,可以采用load()方法
f = open('data/size100/pca_modes.pkl', 'rb')
immean = pickle.load(f)
v = pickle.load(f)
f.close()下面例子使用with()来实现保存和载入操作:
with open('AquaTermi_lowcontrast.jpg','wb') as f:
pickle.dump(immean,f)
pickle.dump(V,f)
with open('AquaTermi_lowcontrast.jpg','rb') as f:
immean = pickle.load(f)
V = pickle.load(f)1.4 Scipy
Scip 是建立在numpy基础之上,用于数值运算的开源工具包。scipy提供很多高效的操作,可以实现数值积分,优化统计,信号处理,以及对我们来说最重要的图像处理功能。
1.4.1 图像模糊
图像的高斯模糊是非常经典的图像卷积例子。本质上,图像模糊就是将图像I和一个高斯核进行卷积操作:
![]()
其中![]() 表示卷积操作,
表示卷积操作,![]() 表示标准差为δ的二维高斯核,定义为:
表示标准差为δ的二维高斯核,定义为:
高斯模糊通常是其他图像处理操作的一部分,比如图像插值操作以及很多其他应用。Scipy有用来做滤波操作的scipy.ndimage.filters 模块。该模块使用快速一维分离的方式来计算卷积。如下所示:
from PIL import Image
from pylab import *
from scipy.ndimage import filters
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
im = array(Image.open('building.jpg').convert('L'))
figure()
gray()
axis('off')
subplot(1, 4, 1)
axis('off')
title(u'原图')
imshow(im)
for bi, blur in enumerate([2, 5, 10]):
im2 = zeros(im.shape)
im2 = filters.gaussian_filter(im, blur)
im2 = np.uint8(im2)
imNum = str(blur)
subplot(1, 4, 2 + bi)
axis('off')
title(u'标准差为:' + imNum)
imshow(im2)
show()
效果图如下:
上面guassian_filter()函数的最后一个参数![]() 表示标准差。随着 越大,处理后的图像细节丢失的越多。
表示标准差。随着 越大,处理后的图像细节丢失的越多。
1.4.2 图像差分
在很多应用中图像强度的变化情况是非常重要的信息。强度的信息可以用灰度图的x和y方向上的导数来描述。图像的梯度向量为:![]()
梯度有两个重要属性:一是梯度的大小,他描述了图像强度变化的强弱,一是梯度的角度:
![]()
描述了图像中的每个点上强度变化的最大方向。Numpy中的![]() 函数返回弧度表示的有符号角度,角度的变化区间为
函数返回弧度表示的有符号角度,角度的变化区间为![]() 。
。
我们可以用离散近似的方式来计算图像的导数。图像导数大多数可以通过卷积简单实现:
![]() 和
和![]()
对于![]() 和
和![]() 通常选择sobel滤波器或prewitt滤波器。这些导数滤波器可以使用scipy.ndimage.filters模块的标准卷积操作来简单地实现。
通常选择sobel滤波器或prewitt滤波器。这些导数滤波器可以使用scipy.ndimage.filters模块的标准卷积操作来简单地实现。
from PIL import Image
from pylab import *
from scipy.ndimage import filters
import numpy
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
im = array(Image.open('building.jpg').convert('L'))
gray()
subplot(4, 4, 1)
axis('off')
title(u'(a)原图')
imshow(im)
# Sobel导数滤波器
imx = zeros(im.shape)
filters.sobel(im, 1, imx)
subplot(4, 4, 2)
axis('off')
title(u'(b)x方向差分')
imshow(imx)
imy = zeros(im.shape)
filters.sobel(im, 0, imy)
subplot(4, 4, 3)
axis('off')
title(u'(c)y方向差分')
imshow(imy)
mag = 255-numpy.sqrt(imx**2+imy**2)
subplot(4, 4, 4)
axis('off')
title(u'(d)梯度幅度')
imshow(mag)
# 高斯差分
def imx(im, sigma):
imgx = zeros(im.shape)
filters.gaussian_filter(im, sigma, (0, 1), imgx)
return imgx
def imy(im, sigma):
imgy = zeros(im.shape)
filters.gaussian_filter(im, sigma, (1, 0), imgy)
return imgy
# there's also gaussian_gradient_magnitude()
def mag(im, sigma):
imgmag = 255 - numpy.sqrt(imgx**2+imgy**2)
return imgmag
sigma = [2, 5, 10]
for i in sigma:
subplot(4, 4, 4+4*(sigma.index(i))+1)
axis('off')
imshow(im)
imgx = imx(im, i)
subplot(4, 4, 4+4*(sigma.index(i))+2)
axis('off')
imshow(imgx)
imgy = imy(im, i)
subplot(4, 4, 4+4*(sigma.index(i))+3)
axis('off')
imshow(imgy)
imgmag = mag(im, i)
subplot(4, 4, 4+4*(sigma.index(i))+4)
axis('off')
imshow(imgmag)
show()上面脚本使用sobel滤波器来计算x和y方向导数,以及梯度大小。sobel()函数的第二个参数表示选择x或者y方向导数,第三个参数保存输出的变量。在以上图像中,正导数显示为亮的像素,负导数显示为暗的像素。灰色区域表示导数的值接近于0。
上诉计算图像导数的方法有一些缺陷:在该方法中,滤波器的尺度需要随着图像分辨率的变化而变化。为了在图像噪声方面更稳健,以及在任意尺度上计算导数,我们可以使用高斯导数滤波器:![]() 和
和![]() 其中
其中 ![]() 和
和 ![]() 表示
表示![]() 在x和y方向上的导数,
在x和y方向上的导数,![]() 为标准差为
为标准差为![]() 的高斯函数。filters.gaussian_filter(im, sigma, (0, 1), imgx)函数的第三个参数指定对每个方向计算哪种类型的导数,第二个参数为使用的标准差。
的高斯函数。filters.gaussian_filter(im, sigma, (0, 1), imgx)函数的第三个参数指定对每个方向计算哪种类型的导数,第二个参数为使用的标准差。
1.4.3 形态学:对象计数
形态学是度量和分析基本形状的图像处理方法的基本框架与集合。形态学通常用于处理二值图像,但是也能够用于灰度图像。二值图像是指图像的每个像素智能取两个值,通常是0和1.二值图像通常是,在计算物体的数目,或者度量其大小时,对一幅图像进行阙值化后的结果。scipy.ndimage 中的morphology模块可以实现形态学操作。你可以使用scipy.ndimage中的measurements模块来实现二值图像的计数和度量功能。
from PIL import Image
from numpy import *
from scipy.ndimage import measurements, morphology
from pylab import *
''' 通过形态计算图片中房屋的数目 '''
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
# load image and threshold to make sure it is binary
figure()
gray()
im = array(Image.open('house.jpg').convert('L'))
subplot(221)
imshow(im)
axis('off')
title(u'原图')
im = (im < 128) # 判断结果为false
labels, nbr_objects = measurements.label(im)
print('Number of objects:', nbr_objects)
subplot(222)
imshow(labels)
axis('off')
title(u'标记后的图')
# morphology - opening to separate objects better
im_open = morphology.binary_opening(im, ones((9, 5)), iterations=2)
subplot(223)
imshow(im_open)
axis('off')
title(u'开运算后的图像')
labels_open, nbr_objects_open = measurements.label(im_open)
print('Number of objects:', nbr_objects_open)
subplot(224)
imshow(labels_open)
axis('off')
title(u'开运算后进行标记后的图像')
show()
上面的脚本首先载入该图像,通过阙值化方式来确保图像是二值图像。通过和1相乘,脚本将布尔数组转换成二进制表示。然后,我们使用label()函数寻找单个的物体,并且按照他们属于哪个对象将整数标签给像素赋值。图像的灰度值表示对象的标签。可以看到,在一些对象之间有一些小的链接。进行二进制的开操作,binary open我们可以将其移除。
binary_opening() 函数的第二个参数指定一个数组结构元素。该数组表示以一个像素为重i性能时,使用哪些相邻像素。在这种情况下,我们在 y方向上使用9个像素,在x方向上使用5个像素。你可以指定任意数组为结构元素,数组中的非零元素决定使用哪些相邻像素。参数iterations决定执行该操作的次数。
效果图:
1.5 图像去噪
图像去噪是在去除噪声的同时,尽可能的保留图像细节和处理技术。我们这里使用ROF(Rudin-Osher-Fatemi)去噪模型。图像去噪对于很多应用来说都很重要,这些应用很广,小到让你的假期照片看起来更漂亮,大到提高卫星图像的质量。ROF模型具有很好的性质:是处理后的图像更加平滑,同时保持图像边缘和结构信息。
from pylab import *
from numpy import random
from scipy.ndimage import filters
from scipy.misc import imsave
from PCV.tools import rof
from PIL import Image
''' 使用ROF模型对图像降噪处理 '''
# 添加中文字体支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
# create synthetic image with noise
'''
im = zeros((500, 500))
im[100:400, 100:400] = 128
im[200:300, 200:300] = 255
im = im + 30*random.standard_normal((500, 500))
'''
im = array(Image.open('building2.jpg').convert('L'))
U, T = rof.denoise(im, im)
G = filters.gaussian_filter(im, 10) # 标准差为:10
# save the result
# imsave('synth_original.pdf',im)
# imsave('synth_rof.pdf',U)
# imsave('synth_gaussian.pdf',G)
figure()
gray()
subplot(131)
imshow(im)
axis('off')
title(u'原噪声图像')
subplot(132)
imshow(G)
axis('off')
title(u'高斯模糊后的图像')
subplot(133)
imshow(U)
axis('off')
title(u'ROF降噪后的图像')
show()
效果图: