第11章:图像金字塔
第11章:图像金字塔
-
- 一、理论基础:
-
- 1. 向下采样:
- 2. 向上采样:
- 二、pyrDown函数使用:
- 三、pyrUp函数及使用:
- 四、采样可逆性研究
- 五、拉普拉斯金字塔
-
- 1. 定义:
- 2. 应用:
什么是图像金子塔?
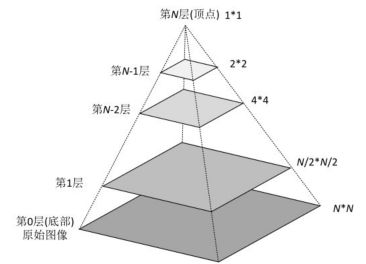
图像金字塔是由一幅图像的多个不同分辨率的子图构成的图像集合。是通过一个图像不断的降低采样率产生的,最小的图像可能仅仅有一个像素点。下图是一个图像金子塔的示例。从图中可以看到,图像金字塔是一系列以金字塔形状排列的、自底向上分辨率逐渐降低的图像集合。
通常情况下,图像金字塔的底部是待处理的高分辨率图像(原始图像),而顶部则为其低分辨率的近似图像。向金字塔顶部移动时,图像的尺寸和分辨率都不断地降低。通常情况下,每向上移动一级,图像的宽和高都降低为原来的二分之一。
一、理论基础:
图像金字塔是同一图像不同分辨率的子图集合,是通过原图像不断地向下降低采样而产生的,即由高分辨率的图像(大尺寸)产生低分辨率的近似图像(小尺寸)。
1. 向下采样:
最简单的图像金字塔可以通过不断的删除图像的偶数行和偶数列得到的。例如,有一幅图像,其大小是N*N,删除其偶数行和偶数列后得到一幅(N/2)*(N/2)大小的图像。经过上述处理后,图像的大小变为原来的四分之一,不断重复该过程,就可以得到该图像的图像金字塔。
也可以通过先对原始图像滤波,得到原始图像的近似图像,然后将近似图像的偶数行和偶数列删除以获取向下采样的结果。有多种滤波器可以选择。
-
领域滤波器:采用邻域平均值计算求原始图像的近似图像。该滤波器能够产生平均金字塔。
-
高斯滤波器:采用高斯滤波器对原始图像进行滤波,得到高斯金字塔。这是OpenCV函数cv2.pyrDown()所采用的的方式。
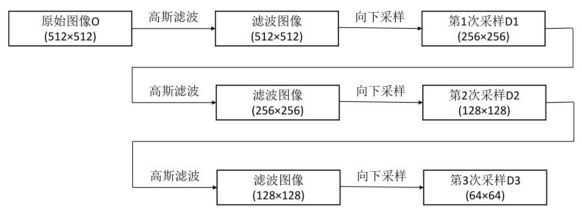
高斯金字塔是通过不断地使用高斯金字塔滤波、采样所产生的,其过程如下:
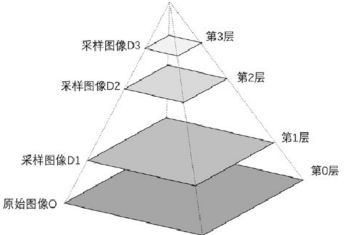
经过上述处理后,原始图像与各次向下采样所得到的结果图像共同构成了高斯金字塔。例如,可以将原始图像称为第0层,第1次向下采样的结果图像称为第一层、第2次向下采样的结果图像称为第2层,以此类推。上述图像所构成的高斯金字塔如图所示。
下面为了表述统一,我们一律将图像金字塔中底层称为第0层,底层上面一层称为第1层,并以此类推。
2. 向上采样:
在向上采样的过程中,通常将图像的宽度和高度都变为原来的2倍。这意味着,向上采样的结果图像的大小是原始图像的4倍。因此,要在结果图像中补充大量的像素点。对新生成的像素点进行赋值的行为,称为 插值。该过程可以通过多种方式实现,例如最邻近插值就是使用最邻近的像素点给当前还没有值的像素点赋值。
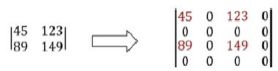
还有一种常见的向上采样,对像素点以补零的方式完成插值。通常是在每列像素点的右侧插入值为零的列,在每行像素点的下方插入值为零的行。如图,左侧是要进行向上采样的4个像素点,右侧是向上采样时进行补零后处理结果。
接下来,使用向下采样时所使用的的高斯滤波器对补零后的图像进行滤波处理,以获取向上采样的结果图像。 但是需要注意,此时图像中有四分之三的像素点的值都是零。所以,要将高斯滤波器系数乘以4,以保证得到的像素值在其原有像素值的范围内。
例如,针对上图右侧的像素点,其对应的是8位图像,像素值的范围是[0, 255]。由于其中四分之三的像素点的值都是为零,如果直接使用高斯滤波器对其进行卷积计算,会导致像素值的范围变为[0, 255*1/4]。所以,要将所使用的高斯滤波器系数乘以4,以保证得到像素值的范围仍旧在[0, 255]内。
或者,从另一个角度理解,在原始图像内每个像素点的右侧列插入零值列,在每个像素点的下一行插入零值行,将图像变为原来的两倍宽、两倍高。接下来,将补零后的图像用高斯滤波器进行卷积运算。最后,将图像内每个像素点的值乘以4,以保证像素值的范围与原始图像一致。
通过以上分析可知,向上采样和向下采样是相反的两种操作。但是,由于上下采样会丢失像素值,所以两种操作并不是可逆的。 也就是说,对一幅图像先向上采样、再向下采样,是无法恢复期原始状态的;同样,对一幅图像先向下采样、再向上采样也是无法恢复到原始状态的。
二、pyrDown函数使用:
在OpenCV中使用函数cv2.pyrDown(),实现图像高斯金字塔操作中的向下采样,语法形式为:
dst = cv2.pyrDown(src [, dstsize [, borderType] ])
- dst:目标图像
- src:原始图像
- dstsize:目标图像的大小
- borderType:边界类型,默认值为BORDER_DEFAULT,且这里仅支持BORDER_DEFAULT。
默认情况下,输出图像的大小为Size((src.cols+1)/2, (src.rows+1)/2)。在任何情况下,图像的尺寸必须满足如下条件:
-
|dst.width * 2 - src.cols| ≤ 2
|dst.height * 2 - src.rows| ≤ 2
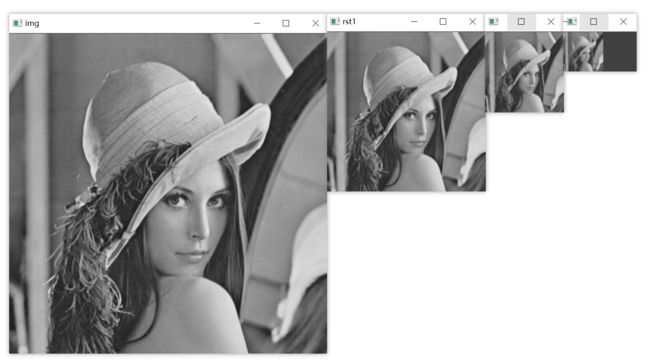
cv2.pyrDown()函数首先对原始图像进行高斯滤波变换,以获取原始图像的近似图像。在获取近似图像后,该函数通过抛弃偶数行和偶数列来实现向下采样。
示例:
import cv2
img = cv2.imread('../lena.bmp')
rst1 = cv2.pyrDown(img)
rst2 = cv2.pyrDown(rst1)
rst3 = cv2.pyrDown(rst2)
print('img.shape=', img.shape)
print('rst1.shape=', rst1.shape)
print('rst2.shape=', rst2.shape)
print('rst3.shape=', rst3.shape)
cv2.imshow('img', img)
cv2.imshow('rst1', rst1)
cv2.imshow('rst2', rst2)
cv2.imshow('rst3', rst3)
cv2.waitKey()
cv2.destroyAllWindows()
# 输出结果
img.shape= (512, 512, 3)
rst1.shape= (256, 256, 3)
rst2.shape= (128, 128, 3)
rst3.shape= (64, 64, 3)
三、pyrUp函数及使用:
在OpenCV中,使用函数cv2.pyrUp()实现图像金字塔操作中的向上采样,其语法格式为:
dst = cv2.pyrUp(src, [, dstsize [, borderType ] ] )
- dst:目标图像
- src:原始图像
- dstsize:目标图像的大小
- borderType:边界类型,默认值为BORDER_DEFAULT,且这里仅支持BORDER_DEFAULT。
默认情况下,输出图像的大小为Size(src.cols*2, src.rows*2)。在任何情况下,图像的尺寸必须满足如下条件:
-
|dst.width - src.cols * 2| ≤ mod(dst.widh, 2)
|dst.height - src.rows * 2| ≤ mod(dst.height, 2)
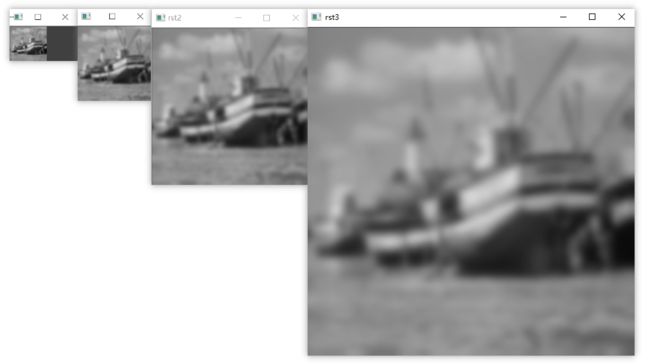
在使用cv2.pyrUp()函数对图像向上采样时,在每个像素的右侧、下方分别插入零值列和零值行,得到一个偶数行、偶数列(即新增的行、列)都是零值的新图像New。接下来,用向下采样时所使用的高斯滤波器对新图像New进行滤波,得到向上采样的结果图像。需要注意的是,为了确保像素值的区间在向上采样后与原始图像保持一致,需要将高斯滤波器的系数乘以4。
示例:
import cv2
img = cv2.imread('../boat.512.tiff')
rst1 = cv2.pyrUp(img)
rst2 = cv2.pyrUp(rst1)
rst3 = cv2.pyrUp(rst2)
print('img.shape=', img.shape)
print('rst1.shape=', rst1.shape)
print('rst2.shape=', rst2.shape)
print('rst3.shape=', rst3.shape)
cv2.imshow('img', img)
cv2.imshow('rst1', rst1)
cv2.imshow('rst2', rst2)
cv2.imshow('rst3', rst3)
cv2.waitKey()
cv2.destroyAllWindows()
# 输出结果
img.shape= (64, 64, 3)
rst1.shape= (128, 128, 3)
rst2.shape= (256, 256, 3)
rst3.shape= (512, 512, 3)
四、采样可逆性研究
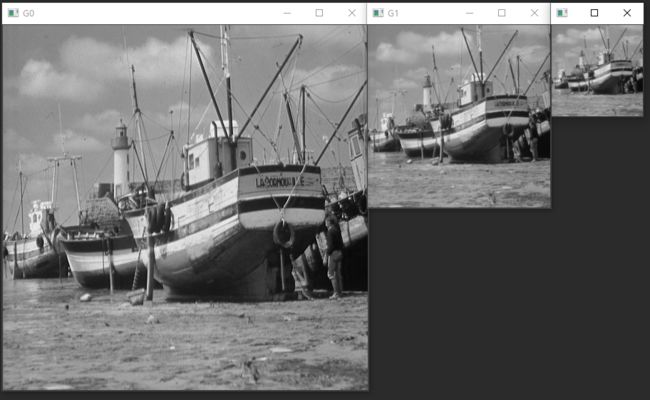
图像在向上采样后,整体尺寸变为原来的4倍;在向下采样后,整体尺寸变为原来的四分之一。下图展示了图像在采样前后的大小变化关系。一幅M*N大小的图像经过向下采样后大小会变为(M/2)*(N/2);一幅M*N大小的图像经过向上采样后大小会变为(2M)*(2N)
虽然一幅图像在先后经过向下采样、向上采样后,会恢复原始大小,但是向上采样和向下采样不是互逆的。也就是说,虽然在经历两次采样操作后,得到的结果图像与原始图像的大小一致,肉眼看起来也相似,但是二者的像素并不是一致的。
示例:
import cv2
img = cv2.imread('../boat.512.tiff')
down = cv2.pyrDown(img)
up = cv2.pyrUp(down)
diff = up - img
print('img.shape=', img.shape)
print('down.shape=', up.shape)
cv2.imshow('img', img)
cv2.imshow('up', up)
cv2.imshow('diff', diff)
cv2.waitKey()
cv2.destroyAllWindows()
# 输出结果
img.shape= (512, 512, 3)
down.shape= (512, 512, 3)
五、拉普拉斯金字塔
前面所介绍的高斯金字塔,是通过对一幅图像一系列的向下采样所产生的。有时,我们希望通过对金字塔中的小图像进行向上采样以获取完整的大尺寸高分辨率图像,这时就需要用到拉普拉斯金字塔。
1. 定义:
一幅图像在经过向下采样后,在对其进行向上采样,是无法恢复为原始状态的。对此,我们也用程序进行了验证。向上采样并不是向下采样的逆运算。这很明显,因为向下采样时在使用高斯滤波器处理后还要抛弃偶数行,偶数列,不可避免的要丢失一些信息。
为了在向上采样是能够恢复具有较高分辨率的原始图像,就要获取在采样过程中所丢失的信息,这些丢失的信息就构成了拉普拉斯金字塔。 也是拉普拉斯金字塔是有向下采样时丢失的信息构成。
拉普拉斯金字塔的定义形式为:
- Li = Gi - pyrUp( Gi + 1 )
式中:
- Li:表示拉普拉斯金字塔中的第i层
- Gi:表示高斯金字塔中的第i层
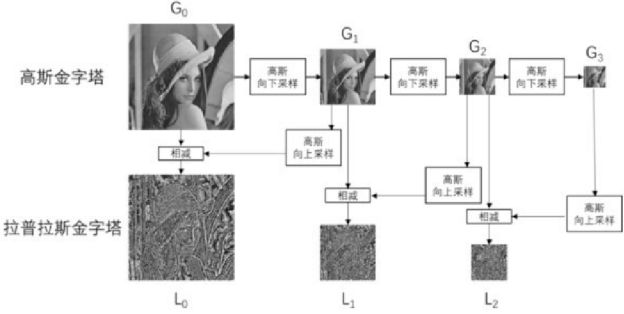
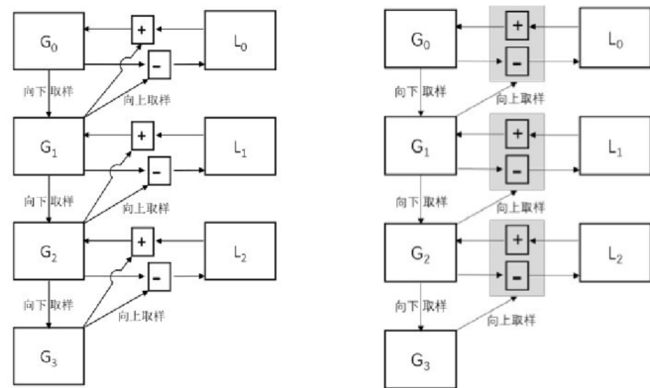
拉普拉斯金字塔中的第i层,等于"高斯金字塔中的第i层"与"高斯金字塔中的第 i + 1层的向上采样结果"之差。下图展示了高斯金字塔和拉普拉斯金字塔的对应关系。
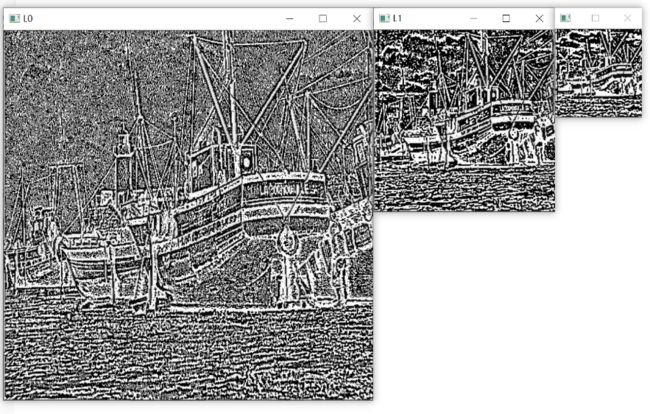
示例:使用cv2.pyrDown()和cv2.pyrUp()构造拉普拉斯金子塔
import cv2
img = cv2.imread('../boat.512.tiff')
G1 = cv2.pyrDown(img)
G2 = cv2.pyrDown(G1)
G3 = cv2.pyrDown(G2)
L0 = img - cv2.pyrUp(G1)
L1 = G1 - cv2.pyrUp(G2)
L2 = G2 - cv2.pyrUp(G3)
print('L0.shape=', L0.shape)
print('L1.shape=', L1.shape)
print('L2.shape=', L2.shape)
cv2.imshow('L0', L0)
cv2.imshow('L1', L1)
cv2.imshow('L2', L2)
cv2.waitKey()
cv2.destroyAllWindows()
# 输出结果
L0.shape= (512, 512, 3)
L1.shape= (256, 256, 3)
L2.shape= (128, 128, 3)
2. 应用:
拉普拉斯金字塔的作用在于,能够恢复高分辨率的图像。下图演示了如何通过拉普拉斯金字塔恢复高分辨率图像。
图中各标记含义如下:
- G0、G1、G2、G3分别是高斯金字塔的第0层、第1层、第2层、第3层。
- L0、L1、L2、分别是拉普拉斯金字塔的第0层、第1层、第2层。
- 向下的箭头表示向下采样操作(对应cv2.pyrDown()函数)
- 向右的箭头表示向上采样操作(对应cv2.pyrUp() 函数)
- "+"表示加法操作
- "-"表示减法操作
上图中的操作关系有:
向下采样:
- G1 = cv2.pyrDown(G0)
- G2 = cv2.pyrDown(G1)
- G3 = cv2.pyrDown(G2)
拉普拉斯金字塔:
- L0 = G0 - cv2.pyrUp(G1)
- L1 = G1 - cv2.pyrUp(G2)
- L2 = G2 - cv2.pyrUp(G3)
向上采样恢复高分辨率图像:
- G0 = L0 + cv2.pyrUp(G1)
- G1 = L1 + cv2.pyrUp(G2)
- G2 = L2 + cv2.pyrUp(G3)
上述关系是通过数学运算推导得到的。例如,已知L0=G0-cv2.pyrUp(G1),将表达式右侧的cv2.pyrUp(G1)移到左侧,就得到了表达式G0 = L0 + cv2.pyrUp(G1)。除此之外,G1和G2都可以通过拉普拉斯金字塔的构造表达式得到。如之前介绍的,拉普拉斯金字塔的目的就是为了恢复高分辨率的图像。
示例:使用拉普拉斯金字塔恢复高分辨率的图像
import cv2
import numpy as np
img = cv2.imread('../boat.512.tiff')
G0 = img
G1 = cv2.pyrDown(G0)
G2 = cv2.pyrDown(G1)
G3 = cv2.pyrDown(G2)
L0 = G0 - cv2.pyrUp(G1)
L1 = G1 - cv2.pyrUp(G2)
L2 = G2 - cv2.pyrUp(G3)
rst_G0 = L0 + cv2.pyrUp(G1)
rst_G1 = L1 + cv2.pyrUp(G2)
rst_G2 = L2 + cv2.pyrUp(G3)
print('rst_G0', np.sum(abs(G0 - rst_G0)))
print('rst_G1', np.sum(abs(G1 - rst_G1)))
print('rst_G2', np.sum(abs(G2 - rst_G2)))
cv2.imshow('G0', G0)
cv2.imshow('G1', G1)
cv2.imshow('G2', G2)
cv2.imshow('rst_G0', rst_G0)
cv2.imshow('rst_G1', rst_G1)
cv2.imshow('rst_G2', rst_G2)
cv2.waitKey()
cv2.destroyAllWindows()