一元多项式相加问题（两种方法）

一元多项式的相加问题，主要运用了线性结构的合并，在合并线性结构的基础上，增加判断，所以我们可以将这个问题理解为一个复杂的线性表合并问题 

目录

问题描述

一、顺序表法

1.1 初始化并创建顺序表

1.2 一元多项式相加算法

1.3 完整代码

二、单链表法

1.1 初始化并创建链表

1.2 一元多项式相加算法

1.3 完整代码

三、运行结果

---

问题描述

【问题描述】

用线性表存放一元多项式，实现两个一元多项式相加，输出结果多项式。
【输入形式】

分两行依次输入两个一元多项式，按指数由低到高依次输入表达式各项的系数和指数，输入字符结束，如果输入的某项系数为0，则不建立该项。

【输出形式】

按指数由低到高依次输出结果表达式各项的系数和指数，如果结果表达式为空则不输出。

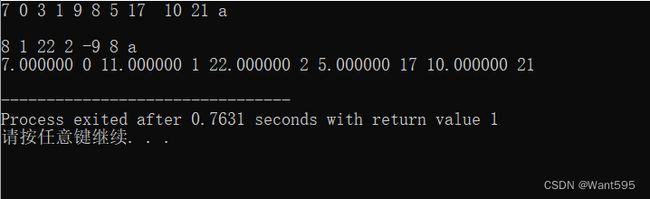
【样例输入1】

7 0 3 1 9 8 5 17  10 21 a

8 1 22 2 -9 8 a

【样例输出1】
7.000000 0  11.000000 1 22.000000 2 5.000000  17 10.000000 21

【样例输入2】

22.2 1 a

-22.2 1 b

【样例输出2】

 

一、顺序表法

利用顺序表实现一元多项式的相加时，我们需要一个存放系数项的数组和一个存放指数项的数组，在执行合并的过程中对指数项进行判断，最后将系数等于零的项删除即可

1.1 初始化并创建顺序表

初始化和创建过程可以参考顺序表的创建，唯一不同的是这里是两个数组而已

typedef struct List{
	double *base1;   //系数，double型变量   （理解为数组）
	int *base2;      //指数，int型变量      （数组）
	int len;
	int size;
}List,*PList;
int Init_List(PList L){
	L->base1=(double*)malloc(sizeof(double)*SIZE);  //初始化
	L->base2=(int*)malloc(sizeof(int)*SIZE);
	L->len=0;
	L->size=SIZE;
	return 1;
}
int Creat_List(PList L){   //创建的时候注意要给系数指数都赋值，其他就是创建顺序表的方法
	double a;
	int b;
	int i=0;
	while(scanf("%lf %d",&a,&b)==2){ 
        if(a==0) continue;         //系数为零时不建立这个项，直接下一次循环 
		if(L->len>=L->size){
			L->base1=(double*)realloc(L->base1,sizeof(double)*(L->size+INCREAM));
			L->base2=(int*)realloc(L->base2,sizeof(int)*(L->size+INCREAM));
			L->size+=INCREAM;
		}
		L->base1[i]=a;
		L->base2[i++]=b;
		L->len++;
	}
	return 1;
}

1.2 一元多项式相加算法

这个算法中一定要注意，当把所有元素都判断完并放入L3中后，一定要小心L3的长度不能忘

int Connect_List(PList L1,PList L2,PList L3){
	int i=0,j=0,k=0;    //分别为L1,L2,L3的下标（L1,L2,L3是数组）
	if(L1->len+L2->len>L3->len){    //判断L3空间是否足够，不够时要重新开辟空间
		L3->base1=(double *)realloc(L3->base1,(L3->size+INCREAM)*sizeof(double));
		L3->base2=(int *)realloc(L3->base2,(L3->size+INCREAM)*sizeof(int));
		L3->size+=INCREAM;
	}
	while(ilen&&jlen){  //循环执行判断，直到一方元素循环完退出循环
		if(L1->base2[i]==L2->base2[j]){ //当L1,L2的指数项相等时，L3的系数项等于两者系数相加
            L3->base1[k]=L1->base1[i]+L2->base1[j++]; 
            L3->base2[k++]=L1->base2[i++];
		}else if(L1->base2[i]base2[j]){  //当L1指数项较小时，L3的系数就是L1
			L3->base1[k]=L1->base1[i];
			L3->base2[k++]=L1->base2[i++];
		}else{                                //当L2指数项较小时，L3的系数就是L2
			L3->base1[k]=L2->base1[j];
			L3->base2[k++]=L2->base2[j++];
		}
	}
	while(ilen){           //另一个循序表里剩余的元素都放入L3
		L3->base1[k]=L1->base1[i];
		L3->base2[k++]=L1->base2[i++];
	}
	while(jlen){          
		L3->base1[k]=L2->base1[j];
		L3->base2[k++]=L2->base2[j++];
	}
	L3->len=k;                //千万不能忘掉L3的长度！！
	for(i=0;ilen;i++){    //最后将L3中系数等于0的项删除
		if(L3->base1[i]==0){
			for(j=i;jlen-1;j++){
				L3->base1[j]=L3->base1[j+1];
				L3->base2[j]=L3->base2[j+1];
			}
			L3->len--;
		}
	}
	return 1;
}

1.3 完整代码

#include
#include
#define SIZE 10
#define INCREAM 10
typedef struct List{
	double *base1;
	int *base2;
	int len;
	int size;
}List,*PList;
int Init_List(PList L){
	L->base1=(double*)malloc(sizeof(double)*SIZE);
	L->base2=(int*)malloc(sizeof(int)*SIZE);
	L->len=0;
	L->size=SIZE;
	return 1;
}
int Creat_List(PList L){
	double a;
	int b;
	int i=0;
	while(scanf("%lf %d",&a,&b)==2){
        if(a==0) continue;
		if(L->len>=L->size){
			L->base1=(double*)realloc(L->base1,sizeof(double)*(L->size+INCREAM));
			L->base2=(int*)realloc(L->base2,sizeof(int)*(L->size+INCREAM));
			L->size+=INCREAM;
		}
		L->base1[i]=a;
		L->base2[i++]=b;
		L->len++;
	}
	return 1;
}
int Print_List(PList L){
	int i;
	for(i=0;ilen;i++){
		printf("%lf %d ",L->base1[i],L->base2[i]);
	}
	printf("\n");
	return 1;
}
int Connect_List(PList L1,PList L2,PList L3){
	int i=0,j=0,k=0;
	if(L1->len+L2->len>L3->len){
		L3->base1=(double *)realloc(L3->base1,(L3->size+INCREAM)*sizeof(double));
		L3->base2=(int *)realloc(L3->base2,(L3->size+INCREAM)*sizeof(int));
		L3->size+=INCREAM;
	}
	while(ilen&&jlen){
		if(L1->base2[i]==L2->base2[j]){
            L3->base1[k]=L1->base1[i]+L2->base1[j++];
            L3->base2[k++]=L1->base2[i++];
		}else if(L1->base2[i]base2[j]){
			L3->base1[k]=L1->base1[i];
			L3->base2[k++]=L1->base2[i++];
		}else{
			L3->base1[k]=L2->base1[j];
			L3->base2[k++]=L2->base2[j++];
		}
	}
	while(ilen){
		L3->base1[k]=L1->base1[i];
		L3->base2[k++]=L1->base2[i++];
	}
	while(jlen){
		L3->base1[k]=L2->base1[j];
		L3->base2[k++]=L2->base2[j++];
	}
	L3->len=k;
	for(i=0;ilen;i++){
		if(L3->base1[i]==0){
			for(j=i;jlen-1;j++){
				L3->base1[j]=L3->base1[j+1];
				L3->base2[j]=L3->base2[j+1];
			}
			L3->len--;
		}
	}
	return 1;
}
int main(){
	List L1,L2,L3;
	Init_List(&L1);
	Init_List(&L2);
	Init_List(&L3);
	Creat_List(&L1);
	getchar();
	Creat_List(&L2);
	Connect_List(&L1,&L2,&L3);
	Print_List(&L3);
	return 0;
}

二、单链表法

运用单链表实现一元多项式相加的过程和顺序表类似，核心算法思想就是循环判断，将指数较小的项放入第三个表，当指数项相等时系数相加放入第三个表

1.1 初始化并创建链表

初始化和创建过程就是创建单链表的过程，唯一不同的也是我们有两个数据域

typedef struct Node{
	double data1;    //系数
	int data2;           //指数
	struct Node * next;
}Node,*PNode;
PNode Init_Node(){           //初始化和创建发放就是链表的创建方法
	PNode head=(PNode)malloc(sizeof(Node));
	head->next=NULL;
	return head;
}
int Creat_Node(PNode head){
	double a;
	int b;
    PNode p=head;
	while(scanf("%lf %d",&a,&b)==2){
        if(a==0) continue;        //系数为0，不建立该项
		PNode q=(PNode)malloc(sizeof(Node));
		q->data1=a;
		q->data2=b;
		p->next=q;
		p=q;
	}
	p->next=NULL;
	return 1;
}

1.2 一元多项式相加算法

算法思想与顺序表相同，循环判断，但是在单链表中，当我们遇到系数相加为零时可以直接释放，不连接到第三个单链表的后面，这正是单链表实现这个问题的一大亮点

PNode Connect_Node(PNode head1,PNode head2,PNode head3){
	PNode p,q,r;
	r=head3;     //第三个单恋表
	p=head1->next;
	q=head2->next;
	while(p&&q){
		if(p->data2data2){    //判断将指数较小的项连接到r后面
			PNode s=(PNode)malloc(sizeof(Node));  //我们需要一个新的临时单链表
			s->data1=p->data1;
			s->data2=p->data2;
			r->next=s;
			r=s;
			p=p->next;
		}else if(p->data2==q->data2){   //当指数项相等时
			PNode s=(PNode)malloc(sizeof(Node));
			s->data1=p->data1+q->data1;   
			s->data2=p->data2;
			if(s->data1==0){  //判断两表系数相加是否为零
				free(s);     //为零时释放s
			}else{
				r->next=s;    //不为零时连接到r后面
				r=s;
			}
			p=p->next;
			q=q->next;
		}else{             //q的指数项较小，连接到r后面
			PNode s=(PNode)malloc(sizeof(Node));
			s->data1=q->data1;
			s->data2=q->data2;
			r->next=s;
			r=s;
			q=q->next;
		}		
	}
	if(p){       //最后还是要判断一下哪个表还有剩余元素，放入r后面
		r->next=p;
	}else if(q){
		r->next=q;
	}else{
		r->next=NULL;
	}
	return r;
}

1.3 完整代码

#include
#include
typedef struct Node{
	double data1;
	int data2;
	struct Node * next;
}Node,*PNode;
PNode Init_Node(){
	PNode head=(PNode)malloc(sizeof(Node));
	head->next=NULL;
	return head;
}
int Creat_Node(PNode head){
	double a;
	int b;
    PNode p=head;
	while(scanf("%lf %d",&a,&b)==2){
        if(a==0) continue;
		PNode q=(PNode)malloc(sizeof(Node));
		q->data1=a;
		q->data2=b;
		p->next=q;
		p=q;
	}
	p->next=NULL;
	return 1;
}
PNode Connect_Node(PNode head1,PNode head2,PNode head3){
	PNode p,q,r;
	r=head3;
	p=head1->next;
	q=head2->next;
	while(p&&q){
		if(p->data2data2){
			PNode s=(PNode)malloc(sizeof(Node));
			s->data1=p->data1;
			s->data2=p->data2;
			r->next=s;
			r=s;
			p=p->next;
		}else if(p->data2==q->data2){
			PNode s=(PNode)malloc(sizeof(Node));
			s->data1=p->data1+q->data1;
			s->data2=p->data2;
			if(s->data1==0){
				free(s);
			}else{
				r->next=s;
				r=s;
			}
			p=p->next;
			q=q->next;
		}else{
			PNode s=(PNode)malloc(sizeof(Node));
			s->data1=q->data1;
			s->data2=q->data2;
			r->next=s;
			r=s;
			q=q->next;
		}		
	}
	if(p){
		r->next=p;
	}else if(q){
		r->next=q;
	}else{
		r->next=NULL;
	}
	return r;
}
int Print_Node(PNode head){
	PNode p=head->next;
	while(p){
		printf("%lf %d ",p->data1,p->data2);
		p=p->next;
	}
	printf("\n");
	return 1;
}
int main(){
	PNode p,q,r;
	p=Init_Node();
	q=Init_Node();
	r=Init_Node();
	Creat_Node(p);
	getchar();
	Creat_Node(q);
	Connect_Node(p,q,r);
	Print_Node(r);
	return 1;
}

三、运行结果