生成式模型(VAE+GAN)

1.VAE-变分自编码器

1.1 交叉熵

1.1.1 信息量

首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设X是一个离散型随机变量，其取值集合为χ,概率分布函数p(x)=Pr(X=x),x∈χ则定义事件X=x₀的信息量为：

由于是概率所以 p(x₀)的取值范围是 [0,1]，且是递减的，当概率越大，信息量越小，可见该函数符合我们对信息量的直觉。）

1.1.2 熵

考虑另一个问题，对于某个事件，有n种可能性，每一种可能性都有一个概率p(x_i)
这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量:

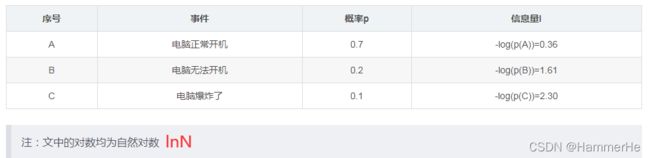
我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：

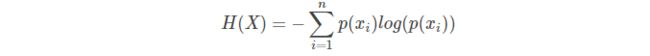
转回关于电脑开机的问题，其中n代表所有的n种可能性（n=3），所以上面的问题结果就是

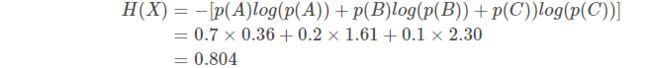
然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，可能性n一定为2，所以熵的计算方法可以简化为如下算式：

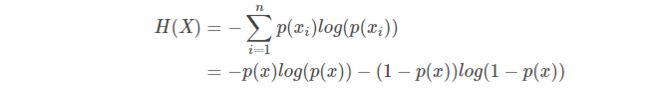
1.1.3 相对熵（KL散度）

相对熵又称KL散度（Kullback-Leibler (KL) divergence）,用来衡量同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)的差异。
大部分情况下，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]。
简单地说KL散度就是如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。
什么是信息增量呢？
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的表达公式：

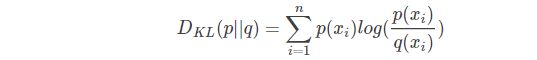
由于结果是信息增量，所以D_KL 的值越小，表示信息增量越少，那么就表示q分布和p分布越接近

注意：KL散度不是对称的，并不满足距离的性质，即：
所以在表示距离的时候往往会采用JS散度度量了两个概率分布的相似度，基于KL散
度的变体，解决了KL散度非对称的问题。一般地，JS散度是对称的，其取值是0到1之间。公式如下：

1.1.4 交叉熵

对DL散度的公式变形可以得到：

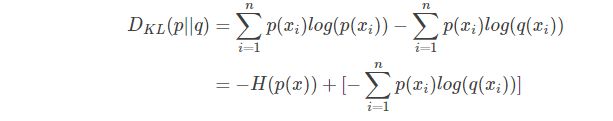
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

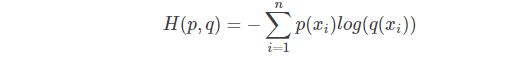
在机器学习中，我们需要评估label（真实标签）和predicts（预测值）之间的差距，使用KL散度刚刚好，即DKL(y||y^)，由于KL散度中的前一部分−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

1.2 MLE（极大似然估计）

1.2.1 MLE的实质

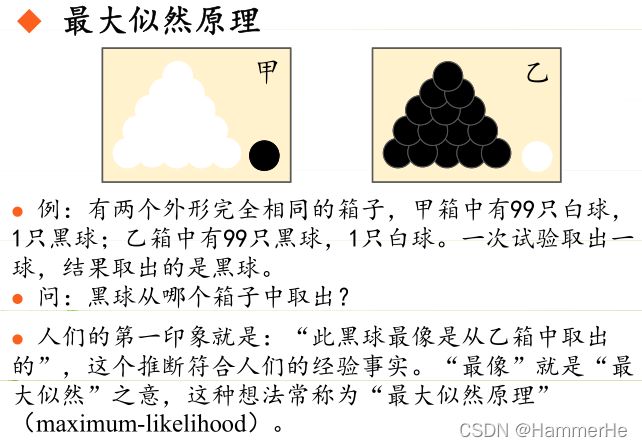
极大似然估计（Maximum Likelihood Estimation），本质就是利用已知样本结果信息，反推对应的模型参数值的过程。
极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。

什么是极大似然原理呢？

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

1.2.2 似然函数公式

由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：

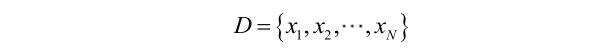
似然函数（linkehood function）：联合概率密度函数p(D|θ)称为相对于D的θ的似然函数，注意∏ 是各项连乘的运算符号:

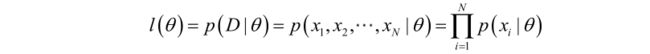
1.2.3 极大似然估计公式

如果^θ是参数空间中能使似然函数l(θ)最大的θ值，则 ^θ 应该是“最可能”的参数值，那么 ^θ就是θ的极大似然估计量。它是样本集的函数，记作：

1.3 VAE模型架构（vs AE-自编码器）

1.3.1 VAE的思路

首先还是从AE（AutoEncoder）谈起：
简单的说自编码器是一类在半监督学习和非监督学习中使用的人工神经网络，其功能是通过将输入信息作为学习目标，对输入信息进行表征学习。
AutoEncoder 包括 编码器(Encoder) 和 解码器(Decoder) 两部分。关于这两部分，之前已经提到很多次了，Encoder 过程是将原先的数据（常用于图像方向）压缩为低维向量；Decoder 则是把低维向量还原为原来数据。但是这种还原方式实际上可以认为是一种“死记硬背”的方式。
所以假如我们希望用Decoder生成一些未曾在已有数据集中出现过的新数据时，AE模型显的无能为力。因为只能是X（源数据）经过Encoder得到的Z（隐变量），才能作为Decoder的合法输入。
用一个例子解释一下AE的这个过程，如下图所示：
我们把一张满月的图片 Encoder 后得到 code(就是z-隐变量)，这个code被decoder 后又转换为满月图，弦月图也是如此。注意它们直接的一对一关系。

假如对 AE中的code进行随机采样时，如图中绿色圈部分的数据，它是介于满月与弦月之间的数据，decoder后可能会输出什么？

可能会输出满月，可能会输出弦月，但是最有可能输出的是奇奇怪怪的图片。这是不可预测的。

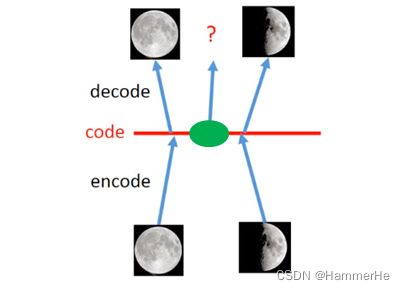
那么为什么会这样呢？
很简单，因为我们不知道z的分布情况，就无法根据分布去生成其他满足条件的z。
所以是不是如果有办法知道了z的分布，就可以从分布中随机采样出新的z，通过Decoder生成新的数据呢？如何去得到这个分布呢？
这就需要我们去控制z的分布了，虽然z的分布未知，但生成z的Encoder却是可以控制的，逻辑上，z也是可以控制的。如果有办法使z满足一个已知的分布，就可以从这个分布中直接采样，然后通过Decoder生成新数据。

还是延续上面的例子在VAE中的实现，对于这一点更为全面的解释可以见这个帖子：
给两张图片编码的时候加上一点噪音，使得每张图片的编码点出现在绿色箭头所示范围内，于是在训练模型的时候，绿色箭头范围内的点都有可能被采样到，这样解码器在训练时会把绿色范围内的点都尽可能还原成和原图相似的图片。然后我们可以关注之前那个失真点，现在它处于全月图和半月图编码的交界上，于是解码器希望它既要尽量相似于全月图，又要尽量相似于半月图，于是它的还原结果就是两种图的折中（3/4全月图）。

也就是说，VAE 产生了输入数据中不包含的数据，（可以认为产生了含有某种特定信息的新的数据）。

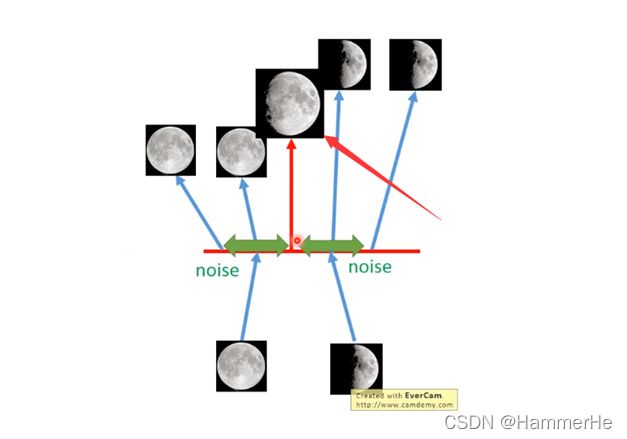由此我们发现，给编码器增添一些噪音（实际上噪音就是满足单位高斯分布的数据），可以有效覆盖失真区域。不过这还并不充分，因为在图中的距离训练区域很远的橘黄色点处（如下图所示），它依然不会被覆盖到，仍是个失真点。

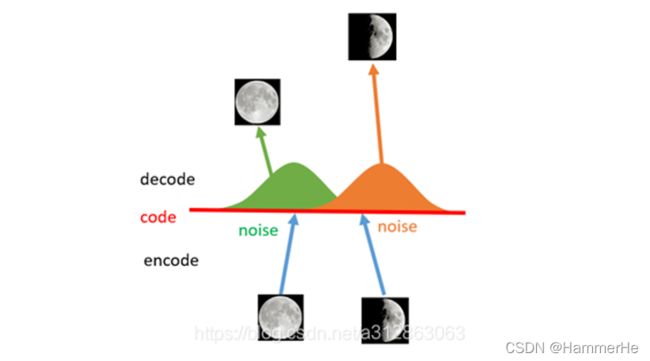
为了解决这个问题，我们可以试图把噪音无限拉长，使得对于每一个样本，它的编码会覆盖整个编码空间，不过我们得保证，在原编码附近编码的概率最高，离原编码点越远，编码概率越低。在这种情况下，图像的编码就由原先离散的编码点变成了一条连续的编码分布曲线

---

所以其实VAE的思路就是训练网络时，给编码网络增加一个约束，使它所生成的隐向量z大体上服从单位高斯分布。之后可以直接从高斯分布中采样得到z，通过Decoder生成新数据。 实际上其他分布也可以，但需要满足： P(X∣z;θ)可计算且在θ处连续，这样我们才可通过梯度下降对其优化。

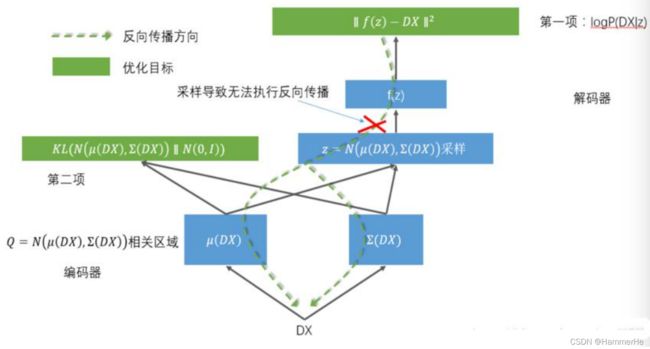
1.3.2 VAE的模型架构

简单的分为三个部分：

---

（1）假定认为输入数据的数据集D(显变量) 的分布完全由一组隐变量 z操控，而这组隐变量之间相互独立而且服从高斯分布，但是目前关于这个高斯分布的参数是未知的，所以我们接下来的目标就是获取这个高斯分布的参数。

---

（2）VAE让 encoder 取学习输入数据的隐变量模型，也就是去学习这组隐变量z的高斯概率分布的参数：隐变量高斯分布的均值(μ)和方差(σ)的log值。

---

(3)而隐变量 z 就可以从这组分布参数的正态分布中采样得到：z∼ N(μ,σ),我们从这组分布中采样也可以获得一些新的数据, 再通过 decoder对z隐变量进行解码来重构输入。

---

我们需要重点关注的一点是学习过程中的目标函数是什么？
包括两部分内容：

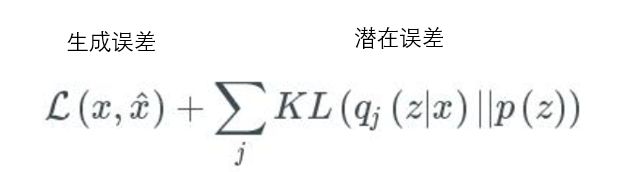
part1:生成误差，用以衡量网络重构图像精确度的均方误差；
第一部分可以理解为关于输入和输出的相似度，就是重建的 loss，就是从 x∼z∼x 的这样一个过程，可以表示成交叉熵的形式。

part2:潜在误差，用以衡量潜在变量在单位高斯分布上的契合程度的KL散度。可以理解为生成隐变量的分布和单位高斯分布的相似度。
如果没有 KL 项，那VAE就退化成一个普通的AE模型，无法做生成，VAE中的隐变量是一个分布，或者说近似高斯的分布，通过对这个概率分布采样，然后再通过decoder网络，VAE可以生成不同的数据，这样VAE模型也可以被称为生成模型。

得到分布以后如何采样构建新的数据？

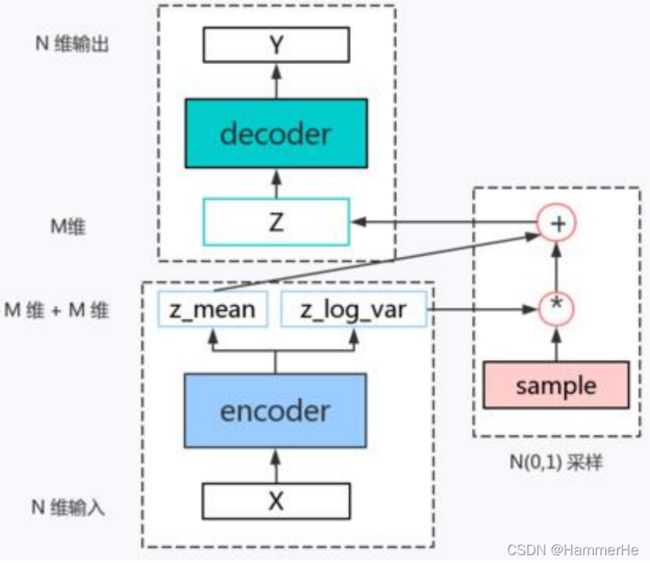
在VAE模型中并没有真正的用z~ N（，） 来采样得到z变量，因为采样之后，无法进行求导。

其做法是先采样一个单位高斯分布(正态分布) E ~ (0,1)，然后得到隐变量=+ E*，这样得到的隐变量z是服从训练得到的z~ N（，）分布，而且就能够对参数（，） 进行正常的求导计算了，如下图所示

基于上述内容得到有关VAE全过程如下所示：

1.3.3 VAE的优点和缺点

优点：遵循“编码-解码”模式，能直接把生成的图像同原始图像进行对比。
不足：由于它是直接采用均方误差，其神经网络倾向于生成较为模糊的图像。

2. GAN

2.1 GAN的初衷和组成

首先我们要确定一件事情：GAN能做什么，为什么要学GAN？
GAN的初衷就是生成不存在于真实世界的数据，类似于使得 AI具有创造力或者想象力。应用场景如下：

(1) AI作家，AI画家等需要创造力的AI体；
(2)将模糊图变清晰(去雨，去雾，去抖动，去马赛克等)，这需要AI具有所谓的“想象力”，能脑补情节；
(3)进行数据增强，根据已有数据生成更多新数据供以feed，可以减缓模型过拟合现象。

GAN和VAE的区别以及GAN的组成
如下图所示：GAN是VAE的“后一半”解码器再加上了一个鉴别网络。由此导致了完全不同的训练方式。

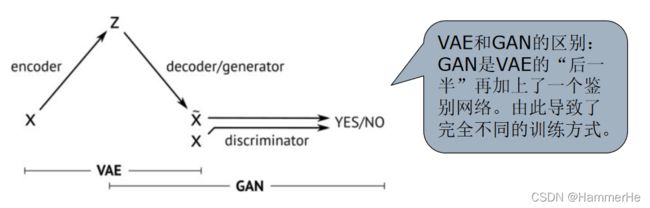
根据上图我们可以把GAN分为两大部分，即G和D

（1）G是generator，生成器: 负责凭空捏造数据出来

生成器主要的内容负责生成样本数据，在生成器网络（深度神经网络（CNN））中输入是高斯白噪声向量 z，而输出则是样本数据向量 x（样本数据就是凭空生成的图像）。可以用下面的公式表示这个过程：
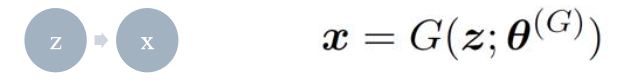θ^G表示的是训练过程中需要学习的参数。

（2）D是discriminator，判别器: 负责判断数据是不是真数据

判别器的主要的内容是负责检测样本数据真假，在判别器网络（深度神经网络（CNN））中输入是真实的数据(x)或生成器生成的样本数据(G(z)),输出的内容是对输入数据判断的真假标签。可以用下面的公式表示这个过程：
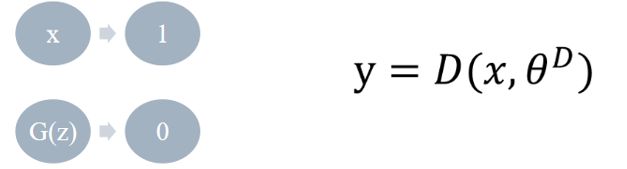参数X代指了真实的数据和生成的样本数据，θ^D表示的是训练过程中需要学习的参数。

至此我们发现GAN可以简单的看作是两个网络的博弈过程。

2.2 GAN的架构和训练

2.2.1 GAN的流程

如下图所示表示了整个GAN的流程：
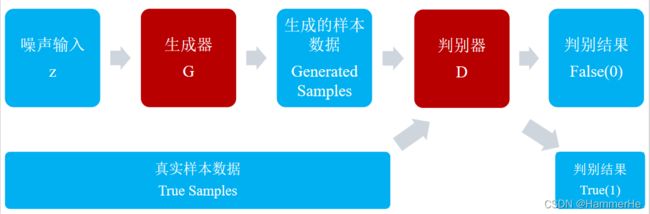对上图流程进行一个解释：
z是随机噪声(就是随机生成的一些数，也就是GAN生成图像的源头)。
D是判别器，它通过真图和假图的数据(相当于天然label)，进行一个二分类神经网络训练。
G是生成器，它根据一串随机数就可以捏造一个“假图像”出来，用这些假图去欺骗D，D负责辨别这是真图还是假图，然后给出一个score用来判别结果。

比如，G生成了一张图，在D这里得分很高，那证明G是很成功的；如果D能有效区分真假图，则G的效果还不太好，需要调整参数。
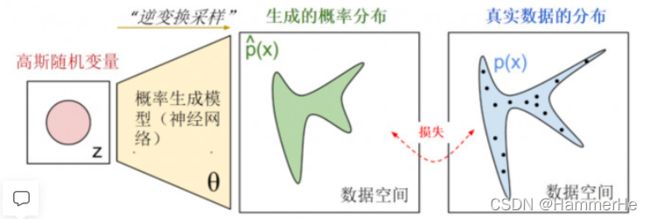
也可以用下面的这个图去理解这个过程，而且从这个图中我们可以明确一点，那就是这个模型希望：通过优化目标，调节概率生成模型的参数θ，从而使得生成的概率分布和真实数据分布尽量接近。：

那么问题来了？怎么样定义优化目标（损失函数）呢？

2.2.2 GAN的优化目标

首先明确判别器的目标是准确的判断某一样本为真实样本还是由生成器生成的虚假样本，输出其为真实样本的概率.所以目标其实分为两个部分：
（1）使得生成器判别真实样本为真实的概率较大，即D(X)尽可能大
（2）为使得生成器判别虚假样本的为真实的概率较小，即D(G(z))尽可能小，即1-D(G(z))尽可能大。
统一两者到一起，所以需要判别器的目标函数就是：

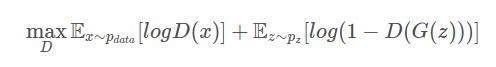
而生成器的目标是尽量生成较为真实的虚假样本，从而使判别器判断该样本为真实样本，所以生成器只有一个目标就是D(G(z))尽可能大，因为D(G(z))越大表示生成的目标越接近真实样本，所以需要生成器的目标函数就是1-D(G(z))尽可能小如下：
如果将生成器目标和判别器目标写为一体，则为：
注意我们发现生成器优化方向其实是最小化目标函数，而判别器优化方向是最大化目标函数，这就说明了一点，两者并不能同时优化，而是需要交替优化（注意优化 D时， G 的参数应当保持不变。反之亦然）判别器目标和生成器目标，直到达到纳什均衡点（Nash equilibrium），才能起到优化生成器和判别器的目的。

那么如何做到交替优化呢，这就需要到一种方法:极大极小博弈(Minimax Game)
由于是交替优化，我们可以从价值函数里面分别得到关于两个优化目标的代价函数J(D)和J(G)。
对于判别器D，代价函数为：
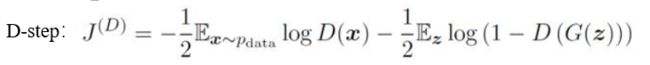对于生成器来说，两者是一个零和博弈，代价综合是零，所以生成器的代价函数满足：
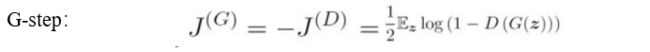而我们的目标就是在博弈中，找到一个纳什平衡点，即为对双方相对来说都较好的结果，即：
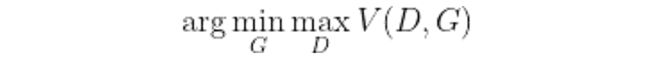这里有个很好的例子就是均衡点是判别器代价函数的鞍点（Saddle Point）

那么如何寻找鞍点呢？

寻找最优判别器：
首先对于最优判别器而言，首要条件是在生成器G固定参数寻找，那么
对于一个具体的样本x，它可能来自真实分布也可能来自生成分布，在固定G参数的情况下，首先考虑它对目标函数的贡献是：
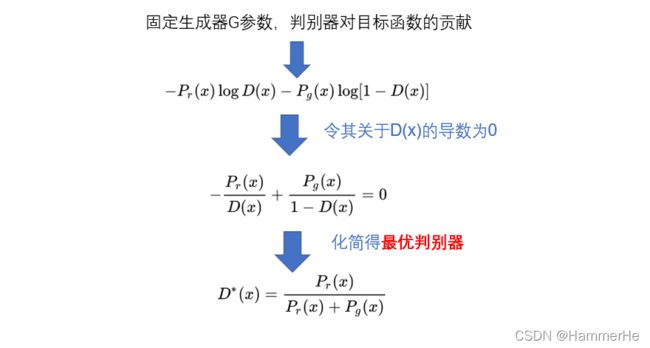这个结果从直观上很容易理解，就是看一个样本x来自真实分布和生成分布的可能性的相对比例。如果P_r(x)=0且P_g(x)≠0，最优判别器就应该非常自信地给出概率0；如果P_r(x)=P_g(x)，说明该样本是真是假的可能性刚好一半一半，此时最优判别器也应该给出概率0.5。

接下来我们把目光转向当判别器最优时，如何寻求最优生成器呢？
方法就是在目标函数中引入Jensen-Shannon散度的概念，之前我们已经介绍了JS散度实际上就是对两个分布相似度的一种距离衡量。
那么在这里目标函数可以转化为如下JS散度形式：
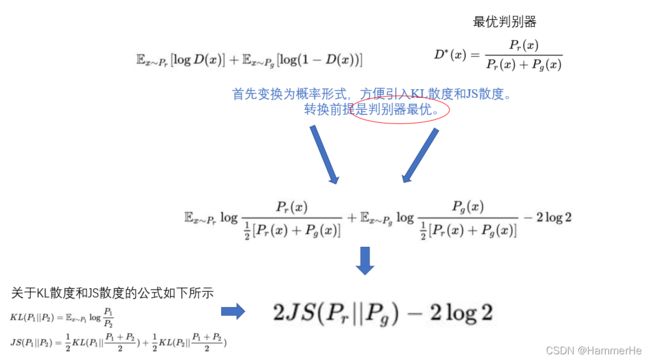如图所示根据原始GAN定义的判别器loss，我们可以得到最优判别器的形式。
而在最优判别器的下，我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布P_r与生成分布P_g之间的JS散度。我们越训练判别器，它就越接近最优，最小化生成器的loss也就会越近似于最小化P_r和P_g之间的JS散度。

2.2.3 GAN的训练

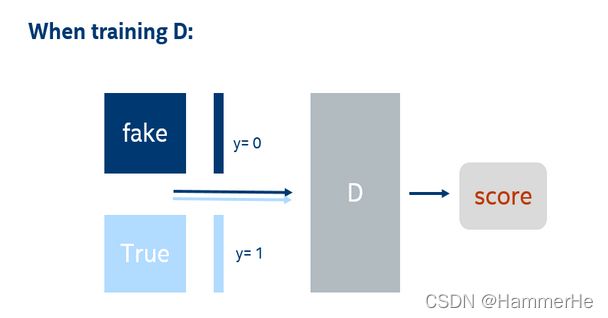
GAN的训练在同一轮梯度反传的过程中可以细分为2步，先训练D在训练G；
注意不是等所有的D训练好以后，才开始训练G，因为D的训练也需要上一轮梯度反传中G的输出值作为输入。

当训练D的时候，上一轮G产生的图片（注意一定要是上一轮的）和真实图片，直接拼接在一起，作为x。然后根据，按顺序摆放0和1，假图对应0，真图对应1。然后就可以通过，x输入生成一个score（从0到1之间的数），通过score和y组成的损失函数，就可以进行梯度反传了。如下图所示（我在图片上举的例子是batch = 1，len(y)=2*batch，训练时通常可以取较大的batch）

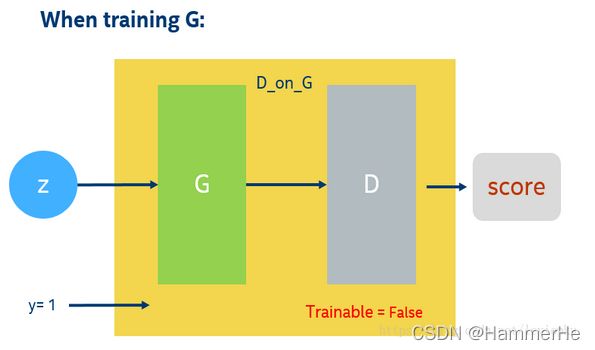
当训练G的时候， 需要把G和D当作一个整体，我在这里取名叫做’D_on_G’。这个整体(下面简称DG系统)的输出仍然是score。输入一组随机向量，就可以在G生成一张图，通过D对生成的这张图进行打分，这就是DG系统的前向过程。score=1就是DG系统需要优化的目标，score和y=1之间的差异可以组成损失函数，然后可以反向传播梯度。注意，这里的D的参数是不可训练的，这是交替优化的要求。这样就能保证G的训练是符合D的打分标准的。这就好比：如果你参加考试，你别指望能改变老师的评分标准。这个过程如下图所示：
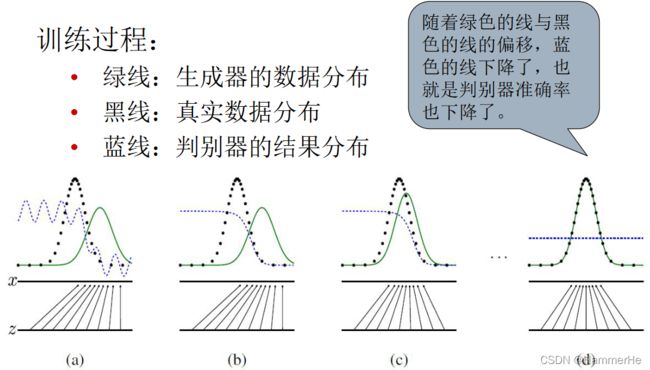
更为具体的训练过程如下所示：
## 2.3 GAN的问题
简单的分为以下三点：
（1）训练困难
• 收敛问题：很难达到纳什均衡点
• 无法有效监控收敛状态，即无监督

（2）模型崩溃（Model collapse）

简单的说是生成器给判别器逼死了，比如说如果某一次G生成的样本可能并不是很真实，但是D给出了正确的评价，或者是G生成的结果中一些特征得到了D的认可，这时候G就会认为我输出的正确的，那么接下来我就这样输出肯定D还会给出比较高的评价，实际上G生成的并不怎么样，但是他们两个就这样自我欺骗下去了，导致最终生成结果缺失一些信息，特征不全。
一般出现在GAN训练不稳定的时候，具体表现为生成出来的结果非常差

• 判别器快速达到最优，能力明显强于生成器，即一直在生成和真实样本一摸一样的东西。
• 生成器将数据集中生成在判别器认最认可的空间点上，即输出多样性很低

（3）不适用于离散输出（不可微分）
• 文本生成：文本数据相比较图片数据来说是离散的，因为对于文本来说，通常需要将一个词映射为一个高维的向量，最终预测的输出是一个one-hot向量，假设softmax的输出是（0.2， 0.3， 0.1，0.2，0.15，0.05）那么变为onehot是（0，1，0，0，0，0），如果softmax输出是（0.2， 0.25， 0.2， 0.1，0.15，0.1 ），one-hot仍然是（0， 1， 0， 0， 0， 0），所以对于生成器来说，G输出了不同的结果但是D给出了同样的判别结果，并不能将梯度更新信息很好的传递到G中去，所以D最终输出的判别没有意义。

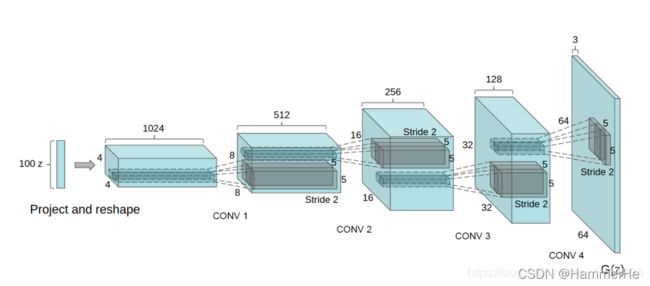
2.4 DCGAN

2.4.1 DCGAN的优化点

（1）全连接层→卷积层

（2）池化层、上采样层→卷积层
生成器：带步长的卷积(Fractional strided convolution)

全卷积网络模型如下：

（3）使用批量归一化（batch normalization）

（4）生成器中使用ReLU激活函数，输出使用Tanh

（5） 判别器中使用Leaky ReLU激活函数

（6）使用adam优化器训练，学习率最好是0.0002

2.4.2 DCGAN生成效果和Z向量的计算特性

生成效果（LSUN数据集上的效果）
• 仅支持低分辨率图片
• 无法捕捉物体结构特性

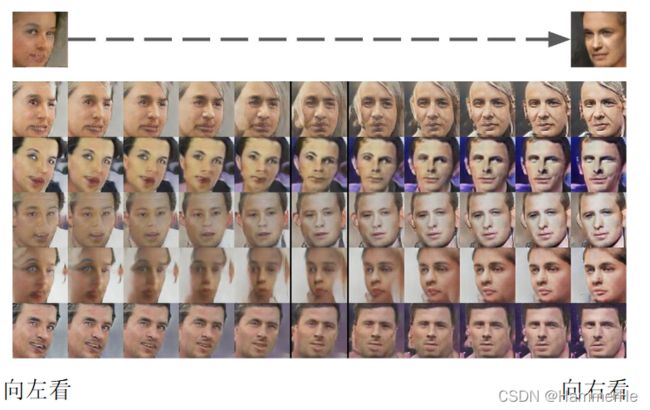
同时DCGAN的作者表明了生成的特征具有向量的计算特性。即特征可以进行“加减”运算和插值运算，如下图所示：
加减运算：
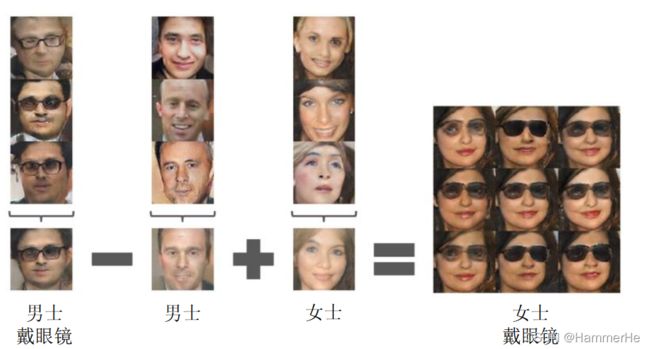插值运算：

2.5 CGGAN

在原始GAN中，目的是使得生成器能够从随机噪声中生成真实数据，而CGAN则更近一层，它希望给GAN加上条件，从而指导数据的生成过程，使得生成的样本具有一些特定的的性质。
以生成MNIST数据集的图像样本来说，原始GAN得到的生成器可以由随机向量生成一张含有数字的图像样本，其中生成的数字可能是0~9中的任意一个
但是CGAN则是在生成器输入时添加一个条件y，这个条件使得可以生成符合预期数字的图像样本，如特定生成生成含有数字1的图像。

根据这样的目标，目标函数变化如下：
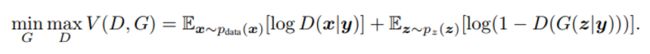输入变量变成了x/y，整个网络过程如下：
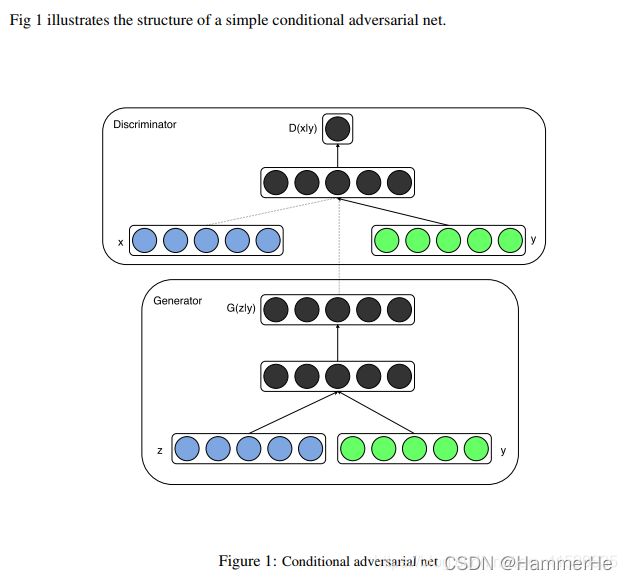主要变化就是G网络的输入在z的基础上连接一个输入y；然后在D网络的输入在x的基础上也连接一个y。

2.6 WGAN

2.6.2 WGAN的优化点

原始GAN问题的根源可以归结为两点，一是等价优化的距离衡量（KL散度、JS散度）不合理，二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠（上升到高维时）从而导致在判别器 优化的很好的时候生成器会有梯度消失的情况发生。

为了使得GAN的训练更加稳定，与DCGAN不同的是，WGAN）主要从目标函数的角度进行改进：
（1）判别器最后一层去掉Sigmoid;
（2）生成器和判别器的loss不取Log;
（3）每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c，即对更新后的参数强制clip到一个区域，如[-0.01，0.01]，以满足连续性条件；
（4）推荐SGD、RMSProp等优化器，不要用基于动量的优化算法（包括momentum和Adam）

2.6.2 对GAN存在问题的再次剖析

首先回顾2.2.2的优化目标推导，在最优判别器的前提下：

在最优判别器的前提下，我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布P_r与生成分布P_g之间的JS散度。我们越训练判别器，它就越接近最优，最小化生成器的loss也就会越近似于最小化P_r和P_g之间的JS散度。
那么问题就来了：
我们会希望如果两个分布之间越接近它们的JS散度越小，我们通过优化JS散度就能将P_r “拉向” P_g，最终以假乱真。

这个希望在两个分布有所重叠的时候是成立的，但是如果两个分布完全没有重叠的部分，或者它们重叠的部分可忽略情况下它们的JS散度是多少呢？ 下面就是推导过程：
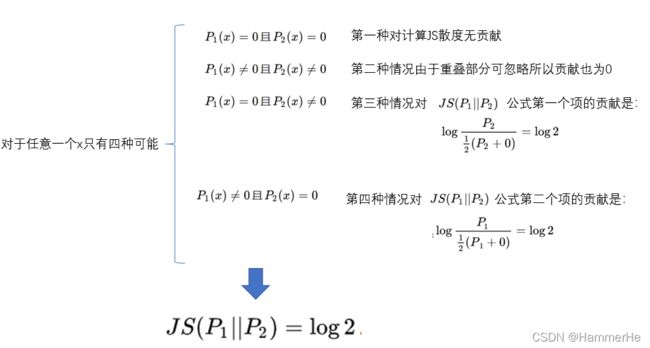换句话说，无论P_r和P_g是远在天边，还是近在眼前，只要它们俩没有一点重叠或者重叠部分可忽略，JS散度就固定是常数log2，而这对于梯度下降方法意味着——梯度为0！此时对于最优判别器来说，生成器肯定是得不到一丁点梯度信息的；即使对于接近最优的判别器来说，生成器也有很大机会面临梯度消失的问题。

那么P_r和P_g不重叠或重叠部分可忽略的可能性有多大？不严谨的说是：非常大。

所以总结下来就是：在（近似）最优判别器下，最小化生成器的loss等价于最小化P_r和P_g之间的JS散度，而由于P_r和P_g几乎肯定有可忽略的重叠，所以无论它们相距多远JS散度都是常数，最终导致生成器的梯度（近似）为0，梯度消失。

2.6.3 Wasserstein距离（推土机距离）

对于解决这个问题的办法在WGAN中就是采用了Wasserstein距离来代替JS散度处理生成器的最优化目标。
所谓的Wasserstein距离又叫Earth-Mover（EM）距离，其实之前在关于颜色特征的距离判断的学习中出现过（可以直接回顾），定义如下：

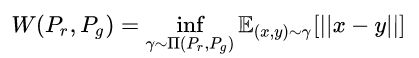
可理解为在这个“路径规划”下把P_r这堆“土”挪到和P_g“位置”所需的“消耗”，而W(P_r,P_g)就是“最优路径规划”下的“最小消耗”。

Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布没有重叠，Wasserstein距离仍然能够反映它们的远近。
下面用一个例子展示了这一点：
KL散度和JS散度是突变的，要么最大要么最小，Wasserstein距离却是平滑的，如果我们要用梯度下降法优化θ这个参数，前两者根本提供不了梯度，Wasserstein距离却可以。类似地，在高维空间中如果两个分布不重叠或者重叠部分可忽略，则KL和JS既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度。

2.6.4从Wasserstein到WGAN

既然Wasserstein距离有如此优越的性质，那么是不是能够把它定义为生成器的loss，不就可以产生有意义的梯度来更新生成器，使得生成分布被拉向真实分布。
并不是这样，这里还存在一个问题：
因为Wasserstein距离定义中的存在如下公式的这一部分是没法直接求解的。
所以首先要把Wasserstein距离转换成如下形式：
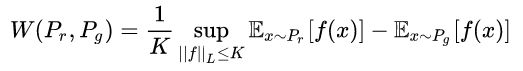首先证明过程尚且不计较，我们先确定以下这个Wasserstein距离形式中表达了什么含义：

（1）Lipschitz连续。它其实就是在一个连续函数f上面额外施加了一个限制，要求存在一个常数K>=0使得定义域内的任意两个元素x₁和x₂都满足:
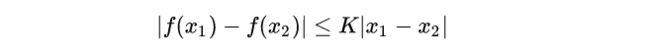此时称函数f的Lipschitz常数为K。
本质意义就是：其实就是在一个连续函数上面额外施加了一个限制，而K就是限制的表现形式。
简单理解，比如说f的定义域是实数集合，那上面的要求就等价于f的导函数绝对值不超过K。

所以由于Lipschitz连续的引入，因为log(x)的导数没有上界，就不是Lipschitz连续，所以原GAN的目标函数中的log(x)不能用了。这正应证了第一项优化点。

（2）由于我们确认了新的距离公式，那么我们是不是可以确定一个学习参数w，那么f就是一个带参数w的神经网络。
到此为止，我们可以构造一个含参数w、最后一层不是非线性激活层的判别器网络f，在限制w不超过某个范围的条件下，使得:

尽可能取到最大，此时L就会近似真实分布与生成分布之间的Wasserstein距离（忽略常数倍数K）。
注意原始GAN的判别器做的是真假二分类任务，所以最后一层是sigmoid，但是现在WGAN中的判别器f_w做的是近似拟合Wasserstein距离，属于回归任务，所以要把最后一层的sigmoid拿掉(这里应证了第二点优化)。
接下来生成器要近似地最小化Wasserstein距离，可以最小化L，由于Wasserstein距离的优良性质，我们不需要担心生成器梯度消失的问题。再考虑到L的第一项与生成器无关，就得到了WGAN的两个loss。

2.6.4 WGAN实验验证结果

主要有三点
（1）判别器所近似的Wasserstein距离与生成器的生成图片质量高度相关。

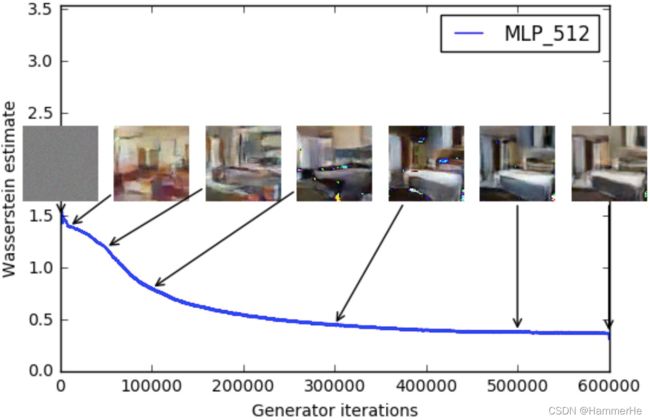
（2）WGAN如果用类似DCGAN架构，生成图片的效果与DCGAN差不多.而且但是厉害的地方在于WGAN不用DCGAN各种特殊的架构设计也能做到不错的效果，比如如果大家一起拿掉Batch Normalization的话，DCGAN就崩了。

（3）在所有WGAN的实验中未观察到collapse mode

2.7 Super-ResolutionGAN

首先什么叫（Super-Resolution）SR ？
从低分辨率(LR)图像中提取高分辨率(HR)图像这一极具挑战性的任务称为超分辨率(SR)。

2.7.1 Super-ResolutionGAN架构

由生成网络和判别网络两部分组成：
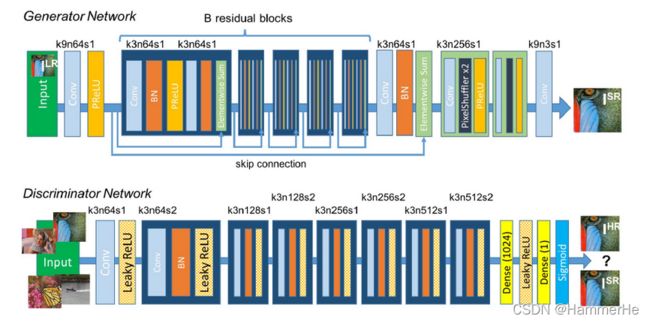生成网络特点：
（1）应用了分布相同的B残差块，每个残差块都有两个卷积层。
（2）卷积层后面加上batch-normalization，并用PReLU作为激活函数。
（3） 卷积层的卷积核都是3×3，并有64个特征图。
（4）利用了跃层连接。
判别网络特点：
（1）由连续的卷积块构成，卷积块包括卷积层、Leaky ReLU层和BN层。
（2）卷积层的卷积核都是3×3。
（3）最后是两个dense层，并通过sigmoid进行鉴别判断。

2.7.2 Super-ResolutionGAN目标函数

首先先确定我们的博弈目标是从低分辨率的输入图像I^LR估计高分辨率、超分辨率的图像I^SR。由此我们可以确定Super-ResolutionGAN的博弈公式（整体目标函数）是：

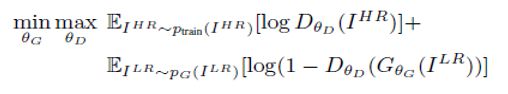
那么生成器目标函数如何获取呢：
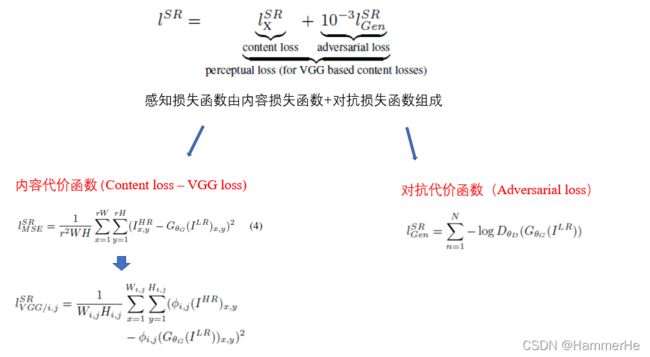
我们的最终目标是训练一个生成函数G_θG来估计给定的LR输入图像与其对应的HR。为了实现这个目标，我们需要优化一个特殊的损失函数l_SR（感知损失函数）对参数θ_G进行学习:

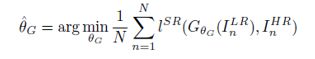
下面介绍感知损失函数：
感知损失函数由内容损失函数+对抗损失函数组成，SR代表超分辨率，LR代表低分辨率，HR代表高分辨率。