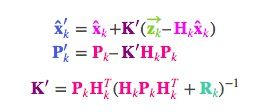我眼中的KF和EKF

什么是卡尔曼滤波

        讲在前面的是卡尔曼滤波上过月球，它的提出者，鲁道夫.E.卡尔曼，在一次访问NASA埃姆斯研究中心时，发现这种方法能帮助解决阿波罗计划的轨道预测问题，后来NASA在阿波罗飞船的导航系统中确实也用到了这个滤波器。最终，飞船正确驶向月球，完成了人类历史上的第一次登月。

        通过其名字我们能知道卡尔曼滤波是一个滤波器，滤波器是用来干嘛的？是用来处理数据的，滤波滤波嘛，就是把一些较为原始的数据或者说较为粗糙的数据进行过滤，使其变得较为光滑，能够满足我们对数据的使用要求。比如我们有一组坐标数据，它描述了小车延x轴直线运动的过程。按理来说，它的坐标轨迹就应该是沿x轴的一条直线。但由于我们测量仪器存在误差，或者是坐标解算的过程出现了问题，它实际得到的坐标轨迹就可能不是一条直线，它可能会上下波动（受噪声影响）。这个上下波动就会影响我们的计算结果，因此我们必须对数据进行处理，数据处理的过程我们就叫它滤波。

        对于这个滤波器，我们几乎可以下这么一个定论：只要是存在不确定信息的动态系统，卡尔曼滤波就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰，卡尔曼滤波通常也能很好的弄清楚究竟发生了什么，找出现象间不易察觉的相关性。它的优点还有内存占用较小（只需保留前一个状态）、速度快，是实时问题和嵌入式系统的理想选择。

他能用来做什么

我们引入一个俗套但容易理解的例子来讲解卡尔曼滤波能用来做啥。

假设有一辆小车在四处溜达，为了实现导航我们需要知道小车的位置信息，为了方便我们使用小车当前的物理位置和当前的速度来表述小车当前的状态，即

。

小车身上装的有GPS传感器，但定位精度有限，我们希望他的定位误差能尽可能得小，因为也许相差一点点就有可能掉进坑里或者撞到树上，但我们的硬件设备(GPS传感器)难免会有精度问题。

我们想一下我们是不是也可以简单地预测小车是怎么移动的，我们假设小车是按照三个方向进行匀速运动的(假设的这个运动模型会有误差，因为它和小车的实际运动模型有出入)，那么我们知道上一时刻的小车状态信息的话我们是不是就能预测到这一时刻的小车的状态信息(在这个例子中通过简单物理公式就能得到)，我们可想而知，小车在运动过程中可能会受到风力的影响或者轮子打滑的情况，这些情况是我们无法用我们的预测模型来进行描述的，即这些误差是系统的误差我们无法避免。预测的方程如下所示：

那么我们有GPS传感器得到的这一时刻的状态信息(注意GPS传感器只能得到位置信息而不能得到速度信息)，也有由上一时刻预测得到的这一时刻的状态信息，那这两个数据进行结合我们是不是能得到一个更为准确的信息呢？答案是肯定的，卡尔曼滤波就是干这件事的。卡尔曼滤波假设两个变量（在我们的例子里是位置和速度）都应该是随机的，而且符合高斯分布。每个变量都有一个均值 μ ，它是随机分布的中心；有一个方差 σ2 ，它衡量组合的不确定性。还需要说明的一点是初始值(第一时刻)的确定，我们一般的做法是直接取第一时刻的观测值当作第一时刻的后验估计值。

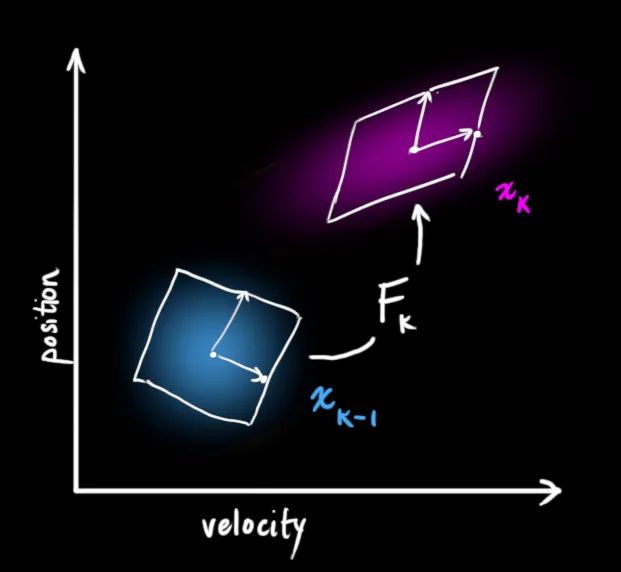
我们把预测过程用运动方程来进行描述，想一下，当只有运动方程时，是不是就相当于我们蒙着眼在一个未知的地方走路，尽管我们知道我们的每一步走了多远，但随着时间的流逝，我们越来越不确定自己的位置，误差是逐渐积累的，我们对位置方差的估计越来越大，但是当我们睁开眼时，由于能不断地观测到外部场景，使得位置估计的不确定性变小。用如下的图为例，我们可以想象的到当没有观测数据时(GPS定位得到的数据)，这个圆会随着运动越来越大，而有了正确的观测数据，圆就会缩小到一定大小保持稳定。

 我们现在对卡尔曼滤波器有了一定的认识，他是用来进行状态估计的，而且卡尔曼滤波只考虑前一时刻的状态，这是卡尔曼滤波的一个特点，这也是为什么他占内存较小的原因。

线性系统和KF

通过上述描述我们知道，卡尔曼滤波器用高斯分布来描述状态信息(即有均值和方差)。我们从最简单的线性高斯系统开始，线性高斯系统是指，运动方程和观测方程都可以由线性方程进行描述。

 我们先来解释一下这两个方程，对于第一个运动方程，为上一时刻的后验状态，我们是已经得到了的，假设其均值为,协方差为(因为随便变量是多维的，所以我们用协方差来表示，与方差意义类似)。其中我们可以先不用管，仅把他理解为我们能够确定下来的外部影响，比如小车的例子中给予小车确定的外力使他前进或者导航发出指令使其加速减速等。

观察下图为运动方程的过程，方程中的状态不只是一个单独数值而是一个高斯分布，既有均值和协方差包含在其中，希望你能够理解。我们说过系统会有很多外部不确定性，例如车轮打滑，风力影响等等，也有由于我们的运动模型与实际的运动模型有出入导致的误差，所以我们的预测会有误差(噪声)，即方程中的Wk，并假设噪声也满足高斯分布，并且服从零均值高斯分析。即  

对于第二个观测方程也不难理解，我们回想一下刚才的例子，小车的GPS传感器得到的测量值为小车的位置信息，但我们使用位置信息和速度信息来进行描述小车的状态，所以我们使用矩阵Hk进行一下转换。由于种种因素，传感器记录的信息其实是不准的，一个状态事实上可以产生多种读数。我们将这种不确定性（即传感器噪声Vk）的协方差设为 Rk 。

根据运动方程我们可以得到预测步的均值和协方差：

所依据的公式为：

我们设读数均值为(在小车的例子中由GPS传感器得到)，协方差为

我们得到两个高斯分布，一块围绕预测的均值，另一块围绕传感器读数。处理这两个高斯分布最简单的办法就是相乘。

下面的式子推导我在这里不做叙述，仅以讲解思想为目的(主要是太菜推不出来)，如若想了解推导过程，网上资料能找到很多。

EKF

讲完KF，EKF就比较好理解了。我们需要理解一点，大部分的运动方程和观测方程通常都是非线性函数。一个高斯分布经过非线性变换后，往往不再是高斯分布，所以在非线性系统中，我们必须取一定的近似，将一个非高斯分布近似成高斯分布。

我们希望把卡尔曼滤波器的结果拓展到非线性系统中，称为拓展卡尔曼滤波器。通常的做法是，在某个点附近考虑运动方程及观测方程的一介泰勒展开，只保留一介项，即线性的部分，然后按照线性系统进行推导。

我们以运动方程为非线性方程为例进行讲解，观测方程同理。还希望在学EKF前你先再温习一下泰勒公式的内容。

假设运动方程为： 同理，我们是用高斯分布来描述状态和噪声。其均值我们可以直接用表示。

我们对其中的在处进行泰勒展开有(写字丑陋还请见谅)，其中 是上一时刻的后验分布，是上一时刻的状态 ：

 我们用表示，则 即为雅可比矩阵，其具体怎么求得牵涉到矩阵的问题，大家自行查阅资料便可，函数F我们确定，则便可求得(理解为常数)，后面的式子类似，则我们可以得到预测步的协方差为 。这样我们就得到了预测步的高斯分布，同理我们可以得到观测步骤的，后续操作同KF一样，这里不再赘述。

本文主要参考：图说卡尔曼图说卡尔曼滤波，一份通俗易懂的教程 - 知乎 (zhihu.com)

 视觉SLAM十四讲第九讲