CMAC小脑模型神经网络与Python实现

CMAC 小脑模型神经网络

简述

CMAC是cerebellar model articulation controller，一种模拟小脑的模型。小脑对肢体动作的操作是近似“反射”的，CMAC的理念就是让训练后的网络在应用时对输入的计算越快越好。很容易想到，最快的方法自然是把所有可能的输入情况和它们对应的输出存在表里，在使用时直接查表。而且为了更快的速度，即使是平衡搜索树也不够，哈希散列技术是一种更有效的技术，只需要预留足够的内存空间，并设计优秀的散列函数就能只花费散列函数计算的时间就查询到结果。

模型搭建

如上图所示，首先对输入的模拟信号进行量化分级，分级的数目根据自己设置的采样率而定。每个级别的量化信号会激活一个区间内的感知器，被激活的感知器把自带的权值做加和成为输出。
其中为了减少感知机的数目，一般使用随机的哈希映射，把量化激活的感知机虚地址映射到实地址。这一点可以有效节约感知器数目，在硬件实现时至关重要。

训练步骤

1. 输入向量的维度有可能很高，因此先把向量做量化是必不可少的。用一定的分辨率采样模拟信号，得到离散的向量。
2. 做合适的感知机激活，为了泛化性能，相似的感知机将被同时激活。体现在模型中就是设置邻域，把输入向量及其附近的感知机都激活。这个激活使用的是一个滚动激活方式，因为多维情形下，每一维的变量都对应一个激活区间。为了理解这一点我们不妨举个例子。
   在二维输入的情形下，两个维度激活的感知机编号分别为1234、2345、3456和abcd、bcde、cdef。
   使用简单的1234、2345、3456的顺序的话，第一个维度的1234和第二个维度的abcd、bcde、cdef结合产生的地址将是
   1a2b3c4d、1b2c3d4e、1c2d3e4f
   而如果我们考虑使用滚动编码的顺序，即1234、5234、5634和abcd、ebcd、efcd。则结合的地址将是
   1a2b3c4d、1e2b3c4d、1e2f3c4d
   可以看出，比起前者，后者让相邻的感知机地址更为接近(相邻的地址只有一位是不同的)。
3. 把第二步中可供选择的感知机都存储下来是不明智的，因为分辨率不能设置的很低，而维度有可能很高，如果为每种情况预留空间，需要的内存将是指数增长的。考虑到维度间的相关性，很多向量情况完全不可能，或者很小概率出现。为此，我们可以考虑把所有地址散列到一个实地址空间内。
4. 输出。网络的最终输出是简单的，使用被激活的几个神经元的权值做叠加。
5. 学习。使用类似前馈网络的学习方法，因为每次激活的神经元数目很少，所以在反馈传播误差时，也只需要做很少的，简单的加减法即可。

综上，CMAC实际上是一种智能查表技术。使用简单的局部性原理，用多个超平面拟合输出超曲面。虽然CMAC做不到RBF和BPN的完全非线性逼近，但CMAC胜在前馈计算速度快，适合智能应用中需要即时反射的场景，而且网络模型更简单，参数更少，计算速度更快。

CMAC实践

CMAC最早的出现是为了解决一个机器人手臂协调的问题，机器人的传感器会返回速度、角度和加速度等信号，它们和力矩满足一个方程，而想从这些信号中计算出应该施加的力矩需要求解反函数，但这个反函数是未知的。为了学习这个反函数，并能满足机器人需要的快速反射，就设计了这种查表型的算法。

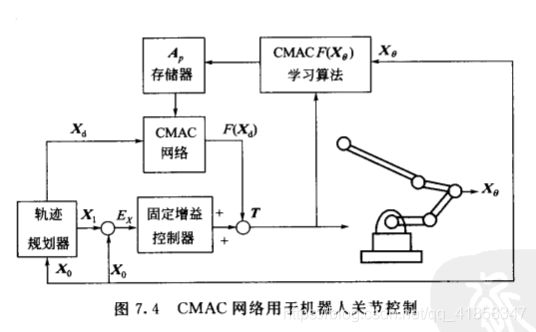
这里我们也用CMAC来学习一个二维输入一维输出的函数，y = sin(x1)cos(x2), 验证本算法的性能。

import numpy as np
import random
import matplotlib.pyplot as plt

def prime(x):
    top = int(x**0.5)+1
    for i in range(2,top):
        if x%i==0:
            return False
    return True

def getprime(x):
    for i in range(x,x**2):
        if prime(i):
            return i
    return False

k = getprime(random.randint(0,1000))
b = getprime(random.randint(0,1000))

def hashing(x,size):
    return (k*x+b)%size



class CMAC:
    def __init__(self,resolution,steps,bottom,C,mem):
        '''
        resolution:模型在各个维度的分辨率
        steps:模型在各个维度采样的步长
        bottom:模型在各个维度采样的起点
        
        C:模型的泛化范围
        mem:模型被分配的实地址数目，也是神经元数目
        为了哈希函数的应用，会在给定的mem向上取到质数
        '''
        self.dim = len(resolution)
        self.C = C
        self.resolution = resolution
        self.steps = steps
        self.bottom = bottom
        #向上取到质数
        self.size = getprime(mem)
        #设置size个权值，用于描述结果
        self.W = np.zeros(self.size)
        #为每个维度的每个可能的量化取值，计算感知器激活情况
        L = max(resolution)
        self.activate = np.zeros((self.dim,L,C))
        for d in range(self.dim):
            self.activate[d][0] = np.array([x for x in range(C)])
            for i in range(1,resolution[d]):
                self.activate[d][i] = self.activate[d][i-1]
                self.activate[d][i][(i-1)%C]+=C
        
        
        
    def forward(self, x):
        #首先解析x，确定每个维度的虚地址
        assert len(x)==self.dim
        dim = self.dim
        address = np.zeros(self.C)#被激活的C个神经元的虚地址
        radix = 1# 由于地址是直接拼接的，每上升一个维度进制要乘以一个值
        for d in range(dim):
            #根据采样步长得到x在该维度的量化取值
            num = int((x[d]-self.bottom[d])//self.steps[d])
            assert num<self.resolution[d]
            #查表找到量化取值num对应的感知器激活情况
            acti = self.activate[d][num]
            address += radix*acti
            radix *= self.resolution[d]+self.C-1
        #使用哈希函数，虚地址转实地址
        address = hashing(address,self.size)
        self.work = address.astype(np.int)
        #实地址对应的神经元权值相加
        self.out = sum(self.W[i] for i in self.work)
        return self.out
    
    def backward(self, yhat, lr):
        total = len(self.work)
        delta = yhat-self.out
        for i in self.work:
            self.W[i] += delta*lr/total
        return
    
    def fit(self, X, Y, lr=0.1, iterations = 1000):
        n = len(X)
        for t in range(iterations):
            i = random.randint(0,n-1)
            x,y = X[i],Y[i]
            self.forward(x)
            self.backward(y,lr)
        return

首先我们定义CMAC的基本架构，代码的注释比较详细，需要知道的都在里面。最上面的随机数生成和质数判断是用于哈希散列的，因为如果使用随机质数系数的线性函数和取模来散列能取得比较好的效果。另外，哈希表的长度，也就是网络里神经元的数目也需要是质数。

#希望模型学习一个函数, f(x1,x2) = sin(x1)cos(x2)
#生成伪数据集
row = np.linspace(0,6.2,300)
col = np.linspace(0,6.2,300)
x1,x2 = np.meshgrid(row,col)
X = np.concatenate((x1.reshape(1,-1),x2.reshape(1,-1)),axis=0).T
Y = np.zeros(90000)
for i in range(len(X)):
    Y[i] = np.sin(X[i][0])*np.cos(X[i][1])

我们在三维空间上制造九万个点用于训练。

model = CMAC([65,65],[0.1,0.1],[0,0],5,5000)
model.fit(X,Y,iterations=20000)
#用3dplot打印model生成的曲面
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import pyplot as plt
xx = np.linspace(0,6,101)
yy = np.linspace(0,6,101)
X,Y = np.meshgrid(xx,yy)
Z = np.zeros(X.shape)
for i in range(len(X)):
    for j in range(len(X[0])):
        x = np.array((X[i][j],Y[i][j]))
        Z[i][j] = model.forward(x)

fig = plt.figure()
axes3d = Axes3D(fig)
axes3d.plot_surface(X,Y,Z,color='grey')

这里建立一个0.1步长，泛化范围(感知器的激活区间)为5，总存储单元5000(会自动向上取到质数)的CMAC网络，经过20000次随机学习，打印出模型学习到的曲面如下。

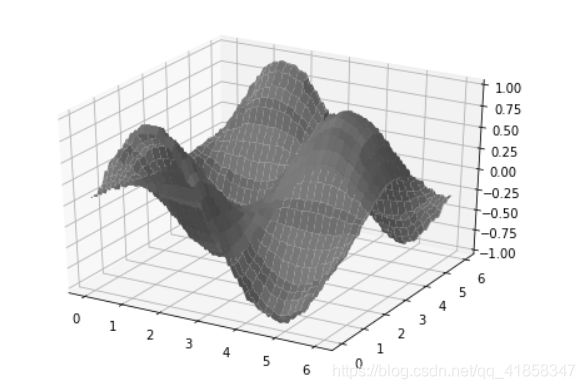
曲面是不光滑的，因为模型实质上是用很多平面去近似目标函数的曲面。这也是它的最大特点，局部近似。

总结

CMAC是一种智能查表技术，说它是神经网络的一种并没错，但似乎有些勉强。
CMAC和前馈网络，RBF径向基网络一样可以逼近非线性函数，但是它是局部逼近。
CMAC的训练速度和响应速度都很快，因为CMAC每次训练只需要更新被激活的几个神经元的权值。而在前馈响应时，只需要计算一下需要激活的神经元的地址，做一个哈希映射，再求和就能得到输出。比起其他深度网络，它需要的计算量非常小，适合用于机器人、证券等对响应时间要求高的领域。