人工智能之数学基础----指数函数和对数函数

本章主要回顾指数函数和对数函数，指数函数和对数函数求导

1. 回顾指数函数和对数函数的基础知识
2. $e$ 的定义和性质
3. 如何对指数函数和对数函数求导
4. 指数函数和对数函数的极限求解
5. 对数函数的微分

基础知识

下面的数表示是一个以2为底，指数为3的幂
$$2^3$$
对于任意底数$b>0$和实数$x$、$y$都满足下面的指数法则

1. 任意非零数的0次幂都等于1$$b^0=0$$
2. 任意数的1次幂就是它本身$$b^1=b$$
3. 将两个底数相同的幂相乘时，将指数相加$$b^x{b}^y=b^{x+y}$$
4. 将两个底数相同的幂相除时，将分子的指数减去分母的指数$$\frac{b^x}{b^y}=b^{x-y}$$
5. 取幂的幂时，指数相乘$$(b^x{)}^y=b^{xy}$$

对数函数回顾

方程$$2^x=7$$中求解$x$，将$x$从指数的位置一下来的方法是对方程取对数
$$x=lo{g}_2(7)$$ 换句话说就是“必须将2提升几次幂才得到7？”，答案是$lo{g}_2(7)$

1. 在方程中底数必须大于0，例如在方程：$(-1{)}^{\frac{1}{2}}$,即：$\sqrt{-1}$；这个方程的底数-1是不是很怪异，所以我们约定指数函数的底数必须大于0
2. 在方程中底数不等于1，设方程$1^x=1$，因为1的任意次方等于1本身，假设现在$x=4$；然后通过对数函数求$x=lo{g}_1(1)$反过来求$x$没有对应的值，所以当底数为1的指数函数是没有研究价值的。
3. 因为底数大于零,并且不等于1，所以$y=b^x>0$；即：$y>0$
   综上所述，在方程中$$y=b^x$$ $$y>0,(b>0,b\ne 1)$$

指数函数、对数函数及反函数

为了加深函数的理解，下面我们通过python可视化来分别讲解

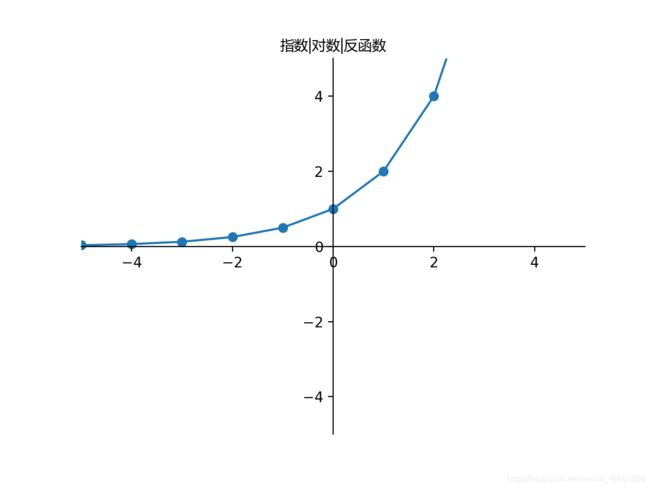
我们就以$$y=2^x$$来讲解，其中$x$定义域是[-5,5]之间，我们列出11个$x$值列表
$$[-5,-4,-3,-2,-1,0,1,2,3,4,5]$$然后将上面的$x$列表代入公式计算得
$$[\frac{1}{32},\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1,2,4,8,16,32]$$现在我们把这些散点图展示在坐标系中，看看效果

def nine():
    plt.figure()
    setting6()      #坐标系设置

    x = np.linspace(-5,5,11,np.float32)  #x轴取[-5,5]区间11个值
    y = np.power(2,x)   #y=2^{x}   y是底数为2的x次方
    
    #下面是为了方便数据可视化，把小数转为分数
    y_list=[]
    for v in y:
        y_list.append(str(Fraction(v)))#把小数转为分数显示

    print(x)
    print(y_list)

打印如下

[-5. -4. -3. -2. -1.  0.  1.  2.  3.  4.  5.]
['1/32', '1/16', '1/8', '1/4', '1/2', '1', '2', '4', '8', '16', '32']

关于坐标系的美化

def setting6():
    plt.gca().set_title("指数|对数|反函数", fontproperties='Microsoft YaHei')
    plt.gca().spines['right'].set_color('none')  # 设置右边框为无色
    plt.gca().spines['top'].set_color('none')  # 设置顶部边框为无色
    plt.gca().spines["bottom"].set_position(('data', 0))  # 设置底边框从数轴0开始
    plt.gca().spines["left"].set_position(('data', 0))  # 设置左边框从数轴0开始
    plt.ylim(-5, 5)  #y轴可视化区域
    plt.xlim(-5, 5)  #x轴可视化区域

打印效果和我们上面分析是一样的，这里显示字符串出吧小数转为分数为了方便可视化做的处理，不用理会

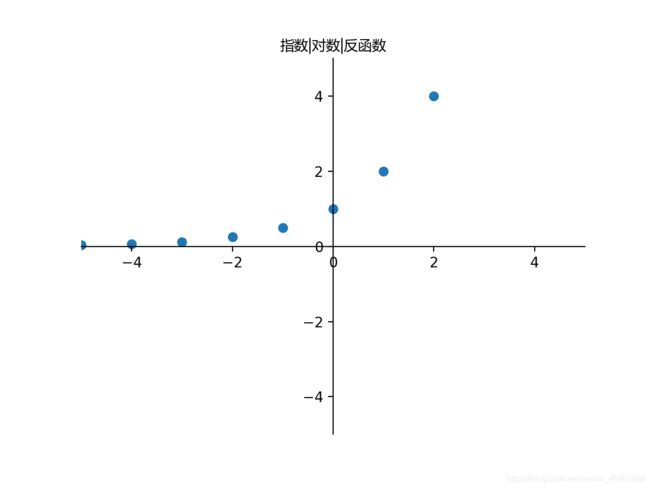
现在我们把上面散点图现在是坐标系，看看效果图，有个直观的理解

在上面的代码追加此行接口

 plt.scatter(x,y)

效果图入线
加入下面的一行代码，把各个点用线连接起来，效果会更加明显

plt.plot(x, y)

这就是函数$f(x)=2^x$的图像，定义域为$\mathbb{R}$任意自然数，值域为$\left(0,+\infty \right)$
该指数函数对应的对数函数为$g(x)=lo{g}_2(x)$，$g(x)$也是$f(x)$的反函数，根据反函数的性质：

1. 原函数$f(x)$的定义域是反函数$g(x)$值域；
2. 原函数$f(x)$的值域是反函数$g(x)$的定义域
   $$g(x)=lo{g}_2(x)$$ $$x\subseteq (0,+\infty );y\subseteq \mathbb{R}$$

根据上面的定义我们可以把指数函数$f(x)$的值域$y$作为对数函数$g(x)$的定义域$x$，看看对数函数$g(x)$计算出来的值是否和指数函数$f(x)$的定义域的值一样

def nine():
    plt.figure(figsize=(4,4))
    setting6()      #坐标系设置

    x = np.linspace(-5,5,11,np.float32)  #x轴取[-5,5]区间11个值
    y = np.power(2,x)   #y=2^{x}   y是底数为2的x次方

    #下面是为了方便数据可视化，把小数转为分数
    y_list=[]
    for v in y:
        y_list.append(str(Fraction(v)))#把小数转为分数显示

    print("f(x)定义域的值：",x)
    print("f(x)值域的值：",y_list)

    plt.scatter(x,y)
    plt.plot(x, y)

    x = y   #把f(x)的值域换成g(x)的定义域
    y = np.log2(x)   #通过对数函数g(x)计算出的值域

    x_list = []
    for v in x:
        x_list.append(str(Fraction(v)))  # 把小数转为分数显示
    print("g(x)定义域的值：",x_list)
    print("g(x)值域的值：",y)

    #绘制可视化图像（对数函数有个直观的了解）
    plt.scatter(x, y)
    plt.plot(x, y)

    plt.show()

代码19行把指数函数f(x)的值域赋值$x$；第20行通过对数函数，该对数函数的底数为2，定义域的值为$x$；最后计算出$y$。第25、26把对数函数的定义域和值域对应的值全部打印出来

f(x)定义域的值： [-5. -4. -3. -2. -1.  0.  1.  2.  3.  4.  5.]
f(x)值域的值： ['1/32', '1/16', '1/8', '1/4', '1/2', '1', '2', '4', '8', '16', '32']
g(x)定义域的值： ['1/32', '1/16', '1/8', '1/4', '1/2', '1', '2', '4', '8', '16', '32']
g(x)值域的值： [-5. -4. -3. -2. -1.  0.  1.  2.  3.  4.  5.]

从结果可以看出，指数函数和对数函数互为反函数，下图是一个直观的了解
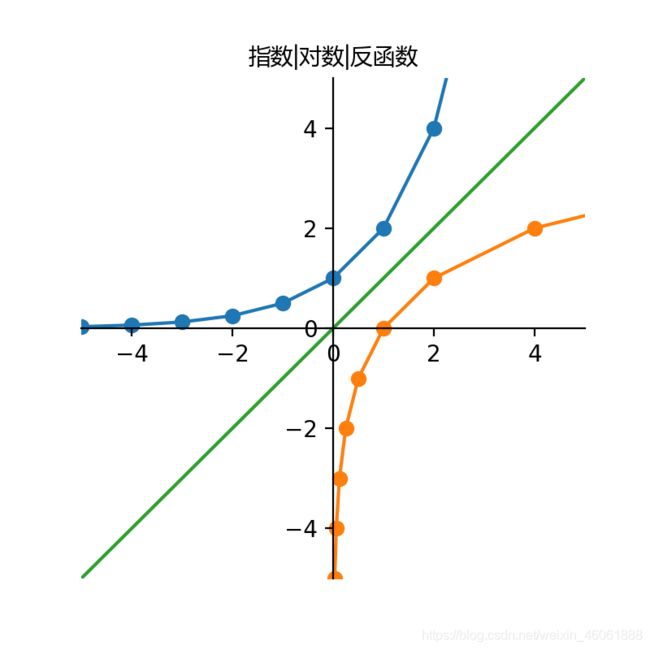从上图可以看出指数函数和对数函数互为反函数，关于$y=x$对称

由于$f(x)$和$g(x)$互为反函数，所以$f(g(x))=x$；$g(f(x))=x$；下面我们根据实例来阐述这个事实

---

1. 令：$f(x)=2^x$；
   $$x=[-5,-4,-3,-2,-1,0,1,2,3,4,5]$$ 那么计算出来对应
   $$y=[\frac{1}{32},\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1,2,4,8,16,32]$$

---

2. 令：$g(x)=lo{g}_2(x)$
   $$x=[\frac{1}{32},\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1,2,4,8,16,32]$$那么计算出来对应
   $$y=[-5,-4,-3,-2,-1,0,1,2,3,4,5]$$

---

$f(x)=2^x=[\frac{1}{32},\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1,2,4,8,16,32]$；大家是否注意指数函数$f(x)$的输出恰好就是对数函数g(x)的输入
因此：$g(x)=g(f(x))=lo{g}_{2}f(x)=lo{g}_2(2^x)=x$

---

$g(x)=lo{g}_{2}x=[-5,-4,-3,-2,-1,0,1,2,3,4,5]$；大家是否注意对数函数$g(x)$的输出恰好是指数函数$f(x)$的输入
因此：$f(x)=f(g(x))=2^{g(x)}=2^{lo{g}_{2}x}=x$

【例】求指数函数$2^x=7$的对数
解：对方程两边去对数
$$lo{g}_2(2^x)=lo{g}_2(7)$$左边的$x$可以提取到前面
$$xlo{g}_2(2)=lo{g}_2(7)$$左边的$lo{g}_2(2)=1$
$$x=lo{g}_2(7)$$
因此：指数函数$2^x=7$的对数为$x=lo{g}_2(7)$

---

对数法则

对于任意的底数$b>1$和正实数$x$、$y$有效法则

1. $lo{g}_b(1)=0$
2. $lo{g}_b(b)=1$
3. $lo{g}_b(xy)=lo{g}_b(x)+lo{g}_b(y)$ 乘积的对数是对数的和
4. $lo{g}_b(\frac{x}{y})=lo{g}_b(x)-lo{g}_b(y)$ 商的对数是对数的差
5. $lo{g}_b(x^y)=ylo{g}_b(x)$ 对数将指数移至对数前面
6. $lo{g}_b(x)=\frac{lo{g}_c(x)}{lo{g}_c(b)}$ 换底法则$b>0$且$c>1$，对于任意$x>0$
   这就说明不同底的对数函数互为常数倍
   $$lo{g}_b(x)=Klo{g}_c(x)$$因为$\frac{1}{lo{g}_c(b)}$不依赖$x$

---

$e$ 的定义和性质

$e$和$\pi$一样,它也是一个特别的数，$e$=2.718 281 828 459 045 23…

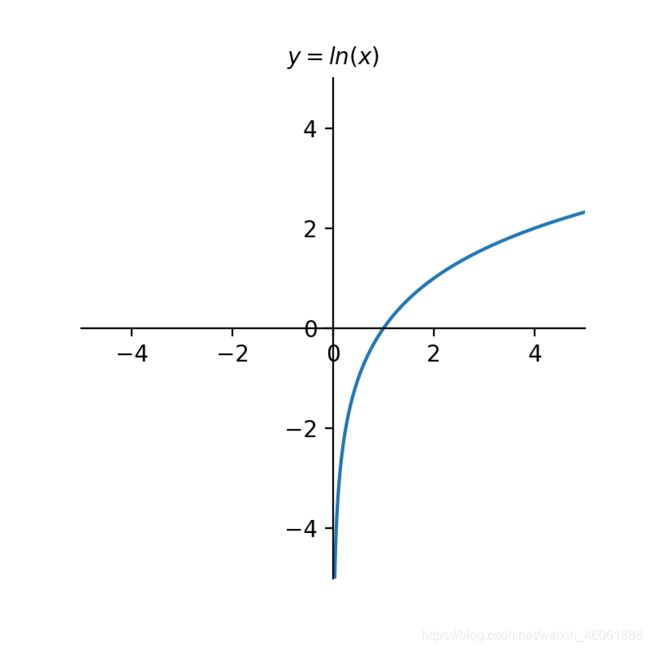
如果$x=e^r$,那么$r=lo{g}_e(x)$，取$e$为底数的对数是十分常见的。但是我们在写法上可以换一种写法：$ln(x)$它等价于$lo{g}_e(x)$，也有人这么写$log(x)$；但是通常我们还是这么写：$ln(x)$

---

下面是一些常用的公式

$$e^{ln(x)}=x$$	$$ln(e^x)=x$$	$$ln(1)=0$$	$$ln(e)=1$$
$$ln(xy)=ln(x)+ln(y)$$	$$ln(\frac{x}{y})=ln(x)-ln(y)$$	$$ln(x^y)=yln(x)$$

---

关于$e$推导出来的一些常用公式

$$\underset{n\to \infty }{\lim }{\left(1+\frac{x}{n}\right)}^n=e^x$$	$$\underset{h\to 0}{\lim }{\left(1+xh\right)}^{\frac{1}{h}}=e^x$$
$$\underset{n\to \infty }{\lim }{\left(1+\frac{1}{n}\right)}^n=e$$	$$\underset{h\to 0}{\lim }{\left(1+h\right)}^{\frac{1}{h}}=e$$

---

指数函数和对数函数求导

【例】令：$g(x)=lo{g}_b(x)$；求对数函数$g(x)$的导数
解：根据求导公式
$$g^{\prime }(x)=\underset{h\to 0}{\lim }\frac{g(x+h)-g(x)}{h}=\underset{h\to 0}{\lim }\frac{lo{g}_b(x+h)-lo{g}_b(x)}{h}$$ 采用对数商法则
$$g^{\prime }(x)=\underset{h\to 0}{\lim }\frac{lo{g}_b(\frac{x+h}{x})}{h}=\underset{h\to 0}{\lim }\frac{lo{g}_b(1+\frac{h}{x})}{h}$$提取$\frac{1}{h}$出来
$$g^{\prime }(x)=\underset{h\to 0}{\lim }\frac{1}{h}lo{g}_b(1+\frac{h}{x})=\underset{h\to 0}{\lim }lo{g}_b(1+\frac{h}{x}{)}^{\frac{1}{h}}$$
现在暂时让我们忘记$lo{g}_b$，当$h$趋于0时
$$\underset{h\to 0}{\lim }{\left(1+\frac{h}{x}\right)}^{\frac{1}{h}}$$ 根据$e$推导所得公式
$$\underset{h\to 0}{\lim }{\left(1+xh\right)}^{\frac{1}{h}}=e^x$$ 令$\frac{1}{x}=r$得
$$\underset{h\to 0}{\lim }{\left(1+rh\right)}^{\frac{1}{h}}=e^r$$ 然后用$r$替换回$\frac{1}{x}$得
$$\underset{h\to 0}{\lim }{\left(1+\frac{1}{x}h\right)}^{\frac{1}{h}}=e^{\frac{1}{x}}$$ 回到$g^{\prime }(x)$表达式
$$g^{\prime }(x)=\underset{h\to 0}{\lim }lo{g}_b(1+\frac{h}{x}{)}^{\frac{1}{h}}=lo{g}_b(e^{\frac{1}{x}})$$ 根据对数法则将指数提取到对数前面
$$g^{\prime }(x)=lo{g}_b(e^{\frac{1}{x}})=\frac{1}{x}lo{g}_b(e)$$ 根据对数换底法则，我们暂且忘掉$\frac{1}{x}$
$$lo{g}_b(e)=\frac{lo{g}_e(e)}{lo{g}_e(b)}=\frac{1}{ln(b)}$$ 代入$g^{\prime }(x)$得
$$g^{\prime }(x)=\frac{1}{xln(b)}$$
根据上面的公式推导得

---

$$\frac{d}{dx}lo{g}_b(x)=\frac{1}{xln(b)}$$

---

如果底数为$e$，那么根据$e$的推导公式得：$ln(e)=1$
$$g^{\prime }(x)=\frac{1}{xln(e)}=\frac{1}{x}$$
公式推导得

---

$$\frac{d}{dx}ln(x)=\frac{1}{x}$$

---

幂函数的求导公式

---

$$\frac{d}{dx}(b^x)=b^{x}ln(b)$$

---

如果底数$b=e$,那么$ln(b)=ln(e)=1$

---

$$\frac{d}{dx}(e^x)=e^x$$

---

注意：这是一个很特殊的导数，因为它的导数等于它本身，无论是一阶导、二阶导、三阶导、四阶导都一样等于它本身

指数函数和对数函数求导例子

【例】求$y=e^{-3x}$的导数
解：令$u=-3x$；那么
$$\frac{du}{dx}=\frac{d}{dx}(-3x)=-3$$ $$\frac{dy}{du}=\frac{d}{dy}(e^u)=e^u$$ 根据链式求导法则
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=e^u(-3)=-3e^{-3x}$$
【例】求$ln(8x)$关于x求导
解：令u=8x；那么
$$\frac{du}{dx}=\frac{d}{dx}(8x)=8$$
$$\frac{dy}{du}=ln(u)=\frac{1}{u}$$
根据链式求导法则
$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=8\times \frac{1}{u}=8\times \frac{1}{8x}=\frac{1}{x}$$

---

指数函数和对数函数的极限

关于极限的计算主要是计算在下面三种情况下的极限值

1. 在0附近
2. 在$\infty$或$-\infty$附近
3. 在某个值$a$附近
   现在我们深入讨论在指数函数和对数函数中的极限，设计到$e$应用

设计$e$定义的极限

【例】求解极限
$$\underset{h\to 0}{\lim }(1+3h^2{)}^{\frac{1}{3h^2}}$$这个极限和我们的$e$推导公式很像
$$\underset{h\to 0}{\lim }(1+h{)}^{\frac{1}{h}}=e$$
因为$h\to 0$，那么 $3h^2\to 0$
所以
$$\underset{h\to 0}{\lim }(1+3h^2{)}^{\frac{1}{3h^2}}=\underset{3h^2\to 0}{\lim }(1+3h^2{)}^{\frac{1}{3h^2}}$$
我们把$3h^2$看做一个整体$v$
$$\underset{3h^2\to 0}{\lim }(1+3h^2{)}^{\frac{1}{3h^2}}=\underset{v\to 0}{\lim }(1+v{)}^{\frac{1}{v}}=e$$
大家可以看到替换后和我们的$e$推导公式一样

---

【例】求解极限
$$\underset{h\to 0}{\lim }(1+sin(h){)}^{\frac{1}{sin(h)}}$$这个极限和我们$e$推导公式很像
$$\underset{h\to 0}{\lim }(1+h{)}^{\frac{1}{h}}=e$$ 因为：$h\to 0$时，$sin(h)\to 0$
所以用$sin(h)$替换$h$得
$$\underset{h\to 0}{\lim }(1+sin(h){)}^{\frac{1}{sin(h)}}=\underset{sin(h)\to 0}{\lim }(1+sin(h){)}^{\frac{1}{sin(h)}}$$
可以把$sin(h)$替换成$v$获取其他字符
$$\underset{sin(h)\to 0}{\lim }(1+sin(h){)}^{\frac{1}{v}}=\underset{v\to 0}{\lim }(1+v{)}^{\frac{1}{v)}}=e$$

---

【例】求解极限
$$\underset{h\to 0}{\lim }(1+cos(h){)}^{\frac{1}{cos(h)}}$$ 由于当$h\to 0$时，那么 $cos(h)\to 1$
因此不能采用$e$推导公式，直接将$h=0$代入计算的
$$(1+1)\frac{1}{1}=2$$
【例】求极限值
$$\underset{h\to 0}{\lim }{\left(1+h^2\right)}^{\frac{1}{3h^2}}$$ 这里我们一样是套用$e$的推导公式，但是因为$h^2$和$3h^2$不同，我们可以吧系数提前出来，是他们相同
$$\underset{h\to 0}{\lim }(1+h^2{)}^{(\frac{1}{h^2}\times \frac{1}{3})}=\underset{h\to 0}{\lim }((1+h^2{)}^{\frac{1}{h^2}}{)}^{\frac{1}{3}}$$ 因为$h\to 0$时，那么 $h^2\to 0$
$$=\underset{h\to 0}{\lim }((1+h^2{)}^{\frac{1}{h^2}}{)}^{\frac{1}{3}}=e^{\frac{1}{3}}$$

---

【例】求解极限
$$\underset{h\to 0}{\lim }(1-5h^3{)}^{\frac{2}{h^3}}$$ 该表达式和$e$推导公式很像
$$\underset{h\to 0}{\lim }(1+xh{)}^{\frac{1}{h}}=3^x$$ 因为$h\to 0$时，那么 $h^3\to 0$；所以我们可以把$h^3$当做$h$看待，把$x=-5$；把$\frac{2}{h^3}$的分子提出来的$\frac{1}{h^3}\times 2$
$$\underset{h\to 0}{\lim }(1+(-5)h^3{)}^{(\frac{1}{h^3}\times 2)}=\underset{h\to 0}{\lim }((1+(-5)h^3{)}^{(\frac{1}{h^3})}{)}^2=e^{-5\times 2}=e^{-10}$$

指数函数在0附近的行为

公式推导得

---

$$\underset{h\to 0}{\lim }\frac{e^h-1}{h}=1$$

---

【例】求解极限
$$\underset{s\to 0}{\lim }\frac{e^{3s^5}-1}{s^5}$$
直接代入上面的公式
$$\underset{s\to 0}{\lim }\frac{e^{3s^5}-1}{3s^5}\times 3=1\times 3=3$$

---

对数函数在1附近的行为

【例】求解方程
$$\underset{h\to 0}{\lim }\frac{ln(1+h)}{h}$$
无论你们是否相信，这是一个导数伪装的极限。设$f(x)=ln(x)$，那么
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}=\underset{h\to 0}{\lim }\frac{ln(x+h)-ln(x)}{h}$$
根据前面$e$导数公式推导的
$$f^{\prime }(x)=\frac{1}{x}$$
所以
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{ln(x+h)-ln(x)}{h}=\frac{1}{x}$$
我们将$x=1$导入
$$f^{\prime }(1)=\underset{h\to 0}{\lim }\frac{ln(1+h)-ln(1)}{h}=\frac{1}{1}=1$$
因为$ln(1)=0$ 简化后的公式

---

$$\underset{h\to 0}{\lim }\frac{ln(1+h)}{h}=1$$

---

【例】求解极限
$$\underset{h\to 0}{\lim }\frac{ln(1-7h^2)}{5h^2}$$
改动分母，使它看起来像$-7h^2$
$$\underset{h\to 0}{\lim }\frac{ln(1-7h^2)}{-7h^2}\times \frac{-7h^2}{5h^2}=1\times \frac{-7}{5}=-\frac{7}{5}$$

---

指数函数在$\infty$和-$\infty$附近的行为

从图像可以看出对数函数$y=e^x$，在当$x\to \infty$时，$y$变得无穷大，当$x\to -\infty$时,$y$变得接近零

$$\underset{x\to \infty }{\lim }{e}^x=\infty$$	$$\underset{x\to -\infty }{\lim }{e}^x=0$$

【例】求解极限
$$\underset{x\to \infty }{\lim }{2}^x和\underset{x\to \infty }{\lim }(\frac{1}{3}{)}^x$$
利用推导公式$A=e^{ln(A)}$
$$\underset{x\to \infty }{\lim }{2}^x=\underset{x\to \infty }{\lim }{e}^{ln(2^x)}=\underset{x\to \infty }{\lim }{e}^{xln(2)}$$
当$x\to \infty$时；$xln(2)\to \infty$，所以
$$\underset{x\to \infty }{\lim }{2}^x=\infty$$

---

$$\underset{x\to \infty }{\lim }(\frac{1}{3}{)}^x=\underset{x\to \infty }{\lim }(\frac{1}{3^x})=\underset{x\to \infty }{\lim }(\frac{1}{e^{ln(3{)}^x}})=\underset{x\to \infty }{\lim }(\frac{1}{e^{xln(3)}})$$
当$x\to \infty$时；$xln(3)\to \infty$，所以$e^{xln(3)}\to \infty$ 其导入
$$\frac{1}{e^{xln(3)}}=0$$
因此：
$$\underset{x\to \infty }{\lim }(\frac{1}{3}{)}^x=0$$
指数增长速度推导公式

$$\underset{x\to \infty }{\lim }\frac{x^n}{e^x}=0$$

注意：不管$n$有多大，上面的公式的分母远远大于分子，因此极限为0

对数在$\infty$附近的行为

$$\underset{x\to \infty }{\lim }ln(x)=\infty$$	$$\underset{x\to 0^{+}}{\lim }ln(x)=-\infty$$

---

对数求导法

【例】求下面的导数
$$\frac{d}{dx}(x^{sin(x)})$$

现在我们要把$sin(x)$拉下来，否则无法求导，令$y=x^{sin(x)}$；对等号两边取相同底数的对数得
$$ln(y)=ln(x^{sin(x)})=sin(x)ln(x)$$ 然后对两边关于$x$进行求导
$$\frac{d}{dx}ln(y)=\frac{d}{dx}sin(x)ln(x)$$ 先看左边是一个关于$x$的隐函数
$$\frac{d}{dx}ln(y)=\frac{1}{y}\frac{dy}{dx}$$ 右边采用求导乘法法则
$$\frac{d}{dx}sin(x)ln(x)=cos(x)ln(x)+\frac{sin(x)}{x}$$ 整理得
$$\frac{1}{y}\frac{dy}{dx}=cos(x)ln(x)+\frac{sin(x)}{x}$$ 两边乘以$y$消掉左边的$\frac{1}{y}$
$$\frac{dy}{dx}=(cos(x)ln(x)+\frac{sin(x)}{x})\times y$$ 用$y=x^{sin(x)}$替换表示的$y$
$$\frac{dy}{dx}=(cos(x)ln(x)+\frac{sin(x)}{x})\times x^{sin(x)}$$