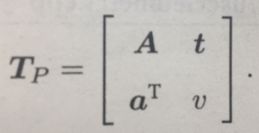3D Vision、SLAM求职宝典 | SLAM知识篇（D1，重点 ）
今日得空，开始愉快的解答！各位看官请指教。
第一部分，先来完成该专题最重要的内容，即笔试面试中所考察的SLAM专业知识。 SLAM知识篇所准备的这些问题不一定全面，但是问题都是基于三位求职者的总结回忆，具有很好的代表性。
可能用到的的参考资料有：
- A）《视觉slam十四讲》，入门slam绝对的好书，理论兼实践，已经看了很多遍；
- B）《机器人状态估计》，已经看完了，经典，书中讲滤波/非线性非高斯过程/李群/位姿估计等等平白中带着严谨，部分内容目前理解不够深；
- C）《计算机视觉：算法与应用》，这本书涉及到视觉的知识很广，包含了图像处理/三维几何/摄影学等等，看了差不多一半，作为参考书是不错的；
- D）《MVG》，多视图几何，slam领域经典中的经典，但是没有书只有电子版，全英文，内容多而深，如有用到我们再查阅；
- E）各种经典的文献，SVO/LSD/ORBSLAM/DSO/Manifold/VINS/PLSLAM等等，真正的把这些好的开源方案理论理解了，并阅读其源码，确实是要花很多时间而且对数学编程要求都不低，博主起步慢做得不好……
- F）网上的各种资源，尤其是各种博客不失为一种高效的学习资源。
为了图省事，很多地方我直接贴照片了。
以下为slam知识篇的D1部分。
目录
1. landmark参数化方式、对比，逆深度参数化；点线面因子图优化
2. 滤波+回环（Trifo-VIO）
3. outlier+鲁棒核、RANSAC
4. EKF更新方程
5. AR系统如何实现
6. 介绍下VO
7. Gridmap（网格标0、1）给定起点和终点，求最优路径（A*或其他路径规划算法）
8. 相似变换、仿射变换、射影变换的区别
9. E和F的区别，自由度计算
10. 单应矩阵H的求取
11. PNP算法、ICP算法（二维码、手眼标定）
12. 闭环检测常用方法（orb、lsd、深度学习）
13. 单目的初始化（拓展：双目，RGBD，VIO的初始化及传感器标定）
14. 简述一下Bundle Adjustment的过程
15. SVO、LSD中深度滤波器原理
16. 说一说某个SLAM框架的工作原理（svo、orb、lsd）及其优缺点，如何改进？
17. RANSAC的框架
18. 位姿不同表示间的相互转化、旋转矩阵特征值和特征向量物理意义
19. 真实世界到相机照片的变换可看成射影变换
20. 直接法与特征点法的优缺点对比
21. 常见滤波方法的对比（KF、EKF、IEKF、UKF、PF）
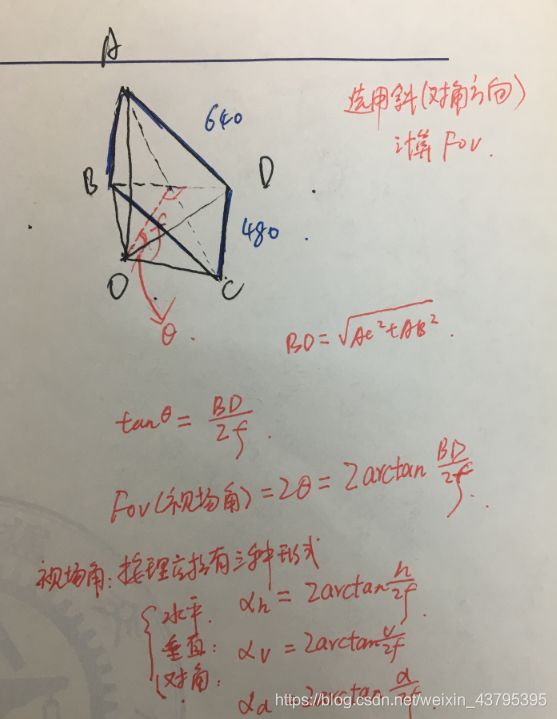
22. 双目测距范围Z=fb/d。问题： 640*480，fov＝90°，zmax＝10m，最小视差为2，求使zmax稳定的最小基线长度（6.25cm）
23. 特征点法与直接法误差模型、Jacobian推导
24. 光流的假设、仿射变换、4种方法，svo采取的方法，优势何在
25. MSCKF与ROVIO、MSCKF与预积分（structureless factor）
26. 边缘化方式原理
1. landmark参数化方式、对比，逆深度参数化；点线面因子图优化
曾以为博客https://blog.csdn.net/weixin_39568744/article/details/88582406 说的比较好。但后来发现，真的是把十四讲上的内容原文不动得搬到了博客上…… 与其看这个博客，不如听我在这里参考十四讲一书并结合自己的经验阐述一下：
- 空间点的参数化： landmark一般点和线两种比较常见，平面我不太了解。关于点，可以用点的x y z 世界坐标来描述，认为三者是随机的，服从三维高斯分布。另一种参数化形式，u v 假设是不动的，一般像素平面图像坐标u v是比较确定的，其不确定性取决于分辨率，而对应的深度d是很不确定的，假设d服从高斯分布。 上述两种参数化的区别，用世界坐标 xyz 描述一个3D点，这三者之间存在着明显的相关性，即协方差矩阵中的非对角元素不为零。 如果用uv d参数化一个点，可以认为uv和d近似独立，甚至uv之间也独立，协方差阵为对角阵，表达更简洁，体现在优化中更方便。
- 单目相机的逆深度问题（inverse depth）： 广泛使用的参数化技巧，我们如果假设深度d满足高斯分布，但实际上这样的假设是不合理的，场景的深度假设为5-10, 则会有更远的点（甚至是无穷远），近处点的深度不可能小于0，这样的分布不太符合高斯分布的图像（引用自十四讲）。 之所以采用逆深度表示我觉得原因有两个： 1. 实际场景中，遇到点的深度可能很远甚至无穷远，遇到的点的深度非常近的较少，采用高斯分布假设，初始值难以覆盖深度很远的点。 这时候用深度的倒数，在数值分布上更符合高斯分布的假设； 2. 实际上应用中，逆深度具有更好的数值稳定性，为啥？ 因为倒数的连续性较好啊， 你想5和10直线差了5，而1/5和1/10之间差的就小多了， 而且仿真发现逆深度的表示更有效，见论文十四讲[115]。
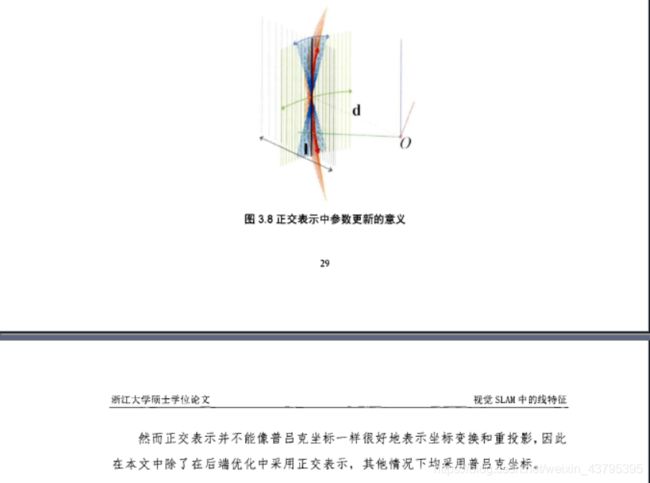
- 空间直线的参数化：点线结合的slam系统的会涉及到线的参数化，一般以直线的两个端点来表达直线居多，但是也会有一些用直线的空间普吕克坐标来表示，下面让我们用很大的篇幅来认识高大上的普吕克坐标参数化直线（来源于谢晓佳硕士论文：基于点线综合特征的双目视觉SLAM方法）
OK！ 这一部分我直接将论文中的内容摘上了，因为感觉确实写得不错。 怎么样，诸君，是不是很高大上？本来简单的两个空间点确定一条直线，生生多了这么多公式！ 但是，不要气馁，多看几遍你总是会看懂的。 这里我来解释一下：
里面有一个很重要的概念，空间直线的自由度是6吗？你可能想象用两个点来确定一条直线，6个自由度；或者一个方向向量，一个平移向量还是6个自由度，但是！ 实际上的空间直线的最小参数化正如上面所说是4，可以理解为一条直线经过SO(3)变换，也就是三个方向的旋转，然后在平移距离d（直线与原点的距离），d属于R，可以为负的。
上面的讨论，给出了两种直线的参数化形式：第一种为直线的普吕克坐标，6个自由度，6维向量，前三维是法向量后三维是方向向量，上述内容还给出了普吕克坐标与普吕克矩阵的关系， 以及这种表示下的投影直线方程； 第二种是直线的最小参数化表示，即正交表示，4个自由度，正交表示表示为（U, W）属于SO(3) *SO(2), 注意这里的SO(3)用李代数来表示为3维向量，SO(2)为二维平面的旋转，是一维向量角度Θ，所以共有四个自由度。同时类似于李代数se(3)到SE(3)的流形增量更新变换，上述内容也给出了直线的流形增量更新直线表达。
评论：论文中两种参数化都用到了，landmark用六自由度的普吕克坐标，在后端优化的时候为了提高迭代稳定性，用到了直线的正交表示。我不知道实际效果怎么样，但是17年有一篇PL_SLAM_mono，以及18年TRO开源的PL_SLAM_stereo 这两篇论文中他们并没有用繁琐的普吕克坐标，而是用直线的端点来参数化直线。所以我觉得并不见的普吕克坐标参数化直线有很大的优势。
关于因子图优化——
先看贝叶斯图：
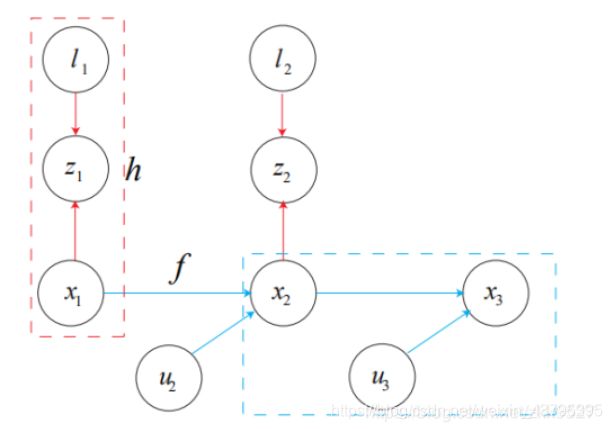路标节点：l（可以点、直线等）; 输入量节点：u； 观测数据节点： z
因子图中，箭头表示了一系列依赖关系，也就是条件概率，例如
通过最大后验概率计算： 
将贝叶斯网络可以转换为因子图。
因子图是无向图，有两种节点组成，一种为优化变量节点，另一种为表示因子的因子节点。
因子图优化： 就是调整各优化变量节点的值，使得各因子乘积最大化。 通常做法中把各因子的条件概率看做高斯分布，因此求最大后验概率相当于取负对数最小化，因此 因子图优化问题最终可以转换为一个最小二乘问题。
因子图的优化和普通的图之间的区别在于： 因子图优化可以增量式的求解，例如08年提出的iSAM，在向因子图中增加节点的时候，通过确定受影响的区域，可以减少优化那些不变要的节点，这样提高了效率。
写起来真是好花时间……
2. 滤波+回环（Trifo-VIO）
SLAM系统的滤波和优化方法笔记 http://blog.sciencenet.cn/blog-465130-1086221.html
Trifo-VIO: Robust and Efficient Stereo Visual Inertial Odometry using Points and Lines
使用点和线的稳健且高效的双目视觉惯导里程计: https://www.cnblogs.com/feifanrensheng/articles/9846151.html
3. outlier+鲁棒核、RANSAC
在最小二乘，即重投影误差最小化的目标函数中，如果一旦出现误匹配，这一部分对目标函数的梯度会影响很大（梯度大），导致偏离正确的优化方向。原因可理解为误差很大时，二范数的增长过快。解决的办法就是引入核函数概念： 将二次函数的改为增长较小的函数，比如常用的Huber核，在小值情况下是二次函数，值值过大的时候退化为一次函数，这样一旦某一项误差项出现误匹配，有这项误差项所引起的目标函数的增长不至于过大，相比于原来，这一项误差项对目标函数的影响就会小很多，不知道你听懂没，反正大概就这么理解的，严格的数学推导书上也没有这里就不追究了。 简而言之，目标函数本来为二次函数，函数值过大时用梯度更增长小的函数代替，这样就限制了梯度的最大值，高斯牛顿法优化的过程中增量更新会较小，这样就不会很受误匹配的影响。 还有Cauchy 核， Tukey核等等。
RANSAC见另一问题。
4. EKF更新方程
图片，来源于《十四讲》：
5. AR系统如何实现
这篇博客不错：https://blog.csdn.net/qq_27489007/article/details/78765810
总结一下：
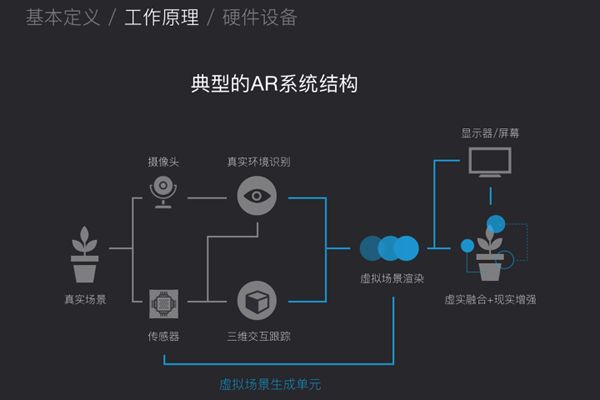
AR增强现实，虚拟影像与现实影像融合，AR技术具有虚拟现实融合、实时交互、三维注册三大特征。AR和VR的区别，除了从硬件和技术等方面有区别，归根到底是要看到底是对现实的增强还是完全的虚拟化。如若是让人们完全投入进入虚拟世界的沉浸感，则是VR。（如超级学校霸王电影里面2人进入街机里面玩超级玛丽），如若是让虚拟的事物和现实接轨，则是AR。（如超级学校霸王电影里面虚拟世界的英雄形象进入真实世界惩罚坏人）而MR则是让2者完全的融合，“实时的”进行虚拟和真实的交互。是最终的发展形态。混合现实是实现虚拟和现实的完美融合。目前的MR和AR可以从设备上来进行区分，有以下2点不同。
首先摄像头和传感器采集真实场景的视频或者图像，传入后台的处理单元对其进行分析和重构，并结合头部跟踪设备的数据来分析虚拟场景和真实场景的相对位置，实现坐标系的对齐并进行虚拟场景的融合计算；交互设备采集外部控制信号，实现对虚实结合场景的交互操作。系统融合后的信息会实时地显示在显示器中，展现在人的视野中。
6. 介绍下VO
里程计一词来源于汽车，轮式里程计可以通过对车轮的转动可以得知汽车的运动距离。对于机器人而言，简单的说里程计就是机器人的运动轨迹，即求解机器人在每一时刻的位姿表示，有六个自由度； 视觉里程计，机器人携带相机作为外传感器，根据实时的视频流，也就是相机图像信息估计机器人的位姿变换，即六自由度（位置和姿态），例如使用单目相机称为单目视觉里程计，两个相机称为立体视觉里程计。
7. Gridmap（网格标0、1）给定起点和终点，求最优路径（A*或其他路径规划算法）
暂时略，歇歇。。。
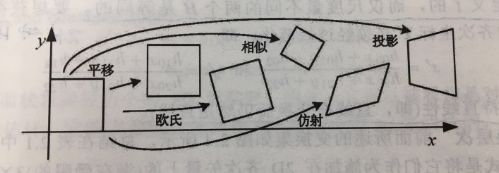
8. 相似变换、仿射变换、射影变换的区别
这三种变换直接拿出《计算机视觉：算法与应用》上的图，保你一目了然。
9. E和F的区别，自由度计算
10. 单应矩阵H的求取
注释：上面按照十四讲所说，H矩阵的求解返回了4种可能的解，但是我记得好像ORBSLAM中说H8种解。
11. PNP算法、ICP算法（二维码、手眼标定）
PNP——
是求解3D-2D点对运动的方法，描述了知道n个3D点及其投影位置时如何求解相机的位姿。最少只要3个点对就可以估计运动。单目相机必须先进行初始化然后才能用pnp，不需要对极约束又可以在很少的点对情况下估计较好的位姿所以很重要。 有很多求解算法： P3P，EPNP，UPNP，DLT直接线性变换，BA等。
- 直接线性变换：公式我就不写了，书上都有，sp=KP等式中取前三维，定义增广矩阵[R|t], 共12个未知数，最少需要6个点对（每个点对提供两个方程，因为其中一个方程用来消去s）。得到的解为一般矩阵，然后进行QR分解，得到近似R，相当于投影到SE(3)的流形上。
- P3P： 3对匹配点，构成一个几何关系，通过余弦定理和相似可以得到三个方程，解析求解用到吴消元法，得到最多四种可能解，这是还需要至少一对验证点，得到最终正确的解。 存在的缺点为：匹配点对多于3很难用到更多的信息； 点对受噪声影响时，or误匹配，算法失效。 一般用P3P、或者EPNP估计位姿初值，然后用BA求解。
- BA： 最小化重投影误差的问题。sp= KT(P), 观测为2D像素坐标，构成了最小二乘问题，可使用LM方法求解，其中用到Jacobi阵，推导见另一个问题。
ICP算法——
3D-3D匹配的点对，求解方法分为两种： 解析解 用到SVD； 或者数值求解，构建BA，最后还是回到解析解。
SVD方法流程： 1. 计算两组点的质心p和p'，计算每个点去质心坐标； 2. W = 求和(qi * qi'T), 对W SVD分解得，W = U*sigma*VT, R = U*VT, 3. 计算t, t = p - Rp'
BA: min(cosi) = 1/2 * 求和[ ( pi - T(pi') )^2.]. 此时，e关于cosi的导数也很好求，略。 ICP特点：极小值就是全局最优解，初始值可以任选。
12. 闭环检测常用方法（orb、lsd、深度学习）
回环检测对于消除SLAM系统长时间运行的漂移有非常重要的作用，如果能够识别到过的地方，那么回环的两端就可以对齐，全局的尺度一致性就能够保证。
1. LSD-SLAM的做法是每当加入一个新关键帧时，通过FABMAP (Glover et al, 2012)中的Appearance Bbased model搜索与空间最近的10个关键帧的匹配，一旦检测到闭环，则对位姿图进行优化，计算相似变换对齐回环两端，并将回环误差分散到到各个关键帧中。
2. ORB-SLAM回环检测使用重定位时同样的基于BoW的地点识别模块，它可以为新加入的关键帧从已有关键帧数据库中高效快速的提取回环候选。为了确信回环和排除干扰，它引入连续一致性约束。确信回环之后，同样计算一个相似变换对齐回环两端。然后对关键帧和地图点进行调整，融合重复的地图点，并且执行一个基于位姿图的全局优化。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
orbslam闭环检测——
泡泡机器人ORBSLAM翻译：
http://www.sohu.com/a/161095723_715754
https://www.sohu.com/a/161346283_715754
http://www.sohu.com/a/154011668_715754
lsdslam闭环检测——
泡泡机器人LSDSLAM的翻译： http://www.jintiankansha.me/t/DqyrBqhRuA
13. 单目的初始化（拓展：双目，RGBD，VIO的初始化及传感器标定）
单目初始化——
对极几何中，t具有尺度等价性，对t乘以任意常数，对极几何约束仍然有效。对地图和轨迹同时缩放任意倍数，得到的图像依然一样。这一点也可以这样理解： 单目两帧图像中如果特征点的深度进行改变，图像中间的特征匹配还是不会变得，对极约束还是存在的。
初始化可以理解为初始化地图的状态，计算出一些3D点，单目因为尺度不确定性，在初始化时对两帧之间的t进行了归一化，两帧图像之间必须有一定程度的平移，以后的地图和轨迹都是以此步的平移为单位。 初始化即求解最开始状态两帧之间的位姿变换并求出3D特征点的位置，单目初始化使用对极约束来求解的，设计本质矩阵或者H矩阵；双目和RGBD的初始化时进行PNP求解， 初始化之后的算法都是进行PNP求解。 初始化的目的是建立三维的空间点和地图，为之后PNP算法计算提供初始值，
可以参考： https://www.jianshu.com/p/52eff860504a
----------------------------------------------------------------------------
推荐orbslam中单目初始
https://blog.csdn.net/zhubaohua_bupt/article/details/78560966
https://www.cnblogs.com/luyb/p/5260785.html
VIO初始化相关paper: https://zhehangt.github.io/2019/03/23/SLAM/Basic/VIOInit/
VIO学习简介： https://blog.csdn.net/qq_40213457/article/details/81298696
VINS初始化及代码： https://zhehangt.github.io/2018/04/19/SLAM/VINS/VINSInitialiaztion/
VI-ORB初始化与VINS初始化对比： https://www.cnblogs.com/mybrave/p/9564899.html
14. 简述一下Bundle Adjustment的过程
所谓的Bundle Adjustment，是指从视觉重建中提炼出最优的3D模型（路标）和相机参数（内参数和外参数，通常内参求得少，主要求相机位姿）。从每一个特征点反射出来的几束光线（bundles of light rays），在我们把相机位姿和特征点空间位置做出最优的调整（adjustment）之后，最后收束到相机光心的这个过程，简称BA。实际上就是最小化重投影误差，求解非线性优化问题，是一种图优化方法。
可以参考：https://blog.csdn.net/weixin_36448497/article/details/82254943
15. SVO、LSD中深度滤波器原理
内容不少，我们放在D2篇来讲述。
16. 说一说某个SLAM框架的工作原理（svo、orb、lsd）及其优缺点，如何改进？
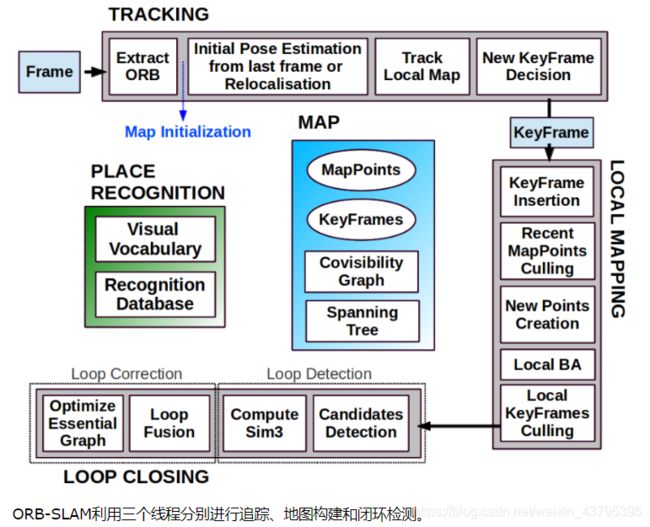
ORBSLAM简介——
（来自吴博讲解https://mp.weixin.qq.com/s?__biz=MzI5MTM1MTQwMw==&mid=2247485193&idx=1&sn=4fe30494a6698f20a874d7ef3e686c7e&scene=21&pass_ticket=sJ9iygLsjWULZokPMkAWD%2FsKkRzO2zTAhqMHg4vq8pfpAJIHoC8coOCAHHuam28I）
该算法以单目为主，但同样适用于双目和RGB-D摄像头。ORB-SLAM算法和PTAM具有相同的算法框架，采用多线程构架，四个主线程：前端位姿跟踪、局部地图构建与优化、闭环检测与优化、显示与交互。
1、前端位姿跟踪线程采用恒速模型，并通过优化重投影误差优化位姿。
2、局部地图线程通过MapPoints维护关键帧之间的共视关系，通过局部BA优化共视关键帧位姿和MapPoints。
3、闭环检测线程通过bag-of-words加速闭环匹配帧的筛选，并通过Sim3优化尺度，通过全局BA优化Essential Graph和MapPoints。
4、使用bag-of-words加速匹配帧的筛选，并使用EPnP算法完成重定位中的位姿估计。
orbslam不足——
1.每幅图像计算orb特征，非常耗时； 2. 三线程CPU负担较重，移植到嵌入式设备有困难； 3. 稀疏图无法满足导航避障互动等
17. RANSAC的框架
简介： https://blog.csdn.net/robinhjwy/article/details/79174914
算法伪代码——
伪码形式的算法如下所示：
输入：
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出：
best_model —— 跟数据最匹配的模型参数（如果没有找到好的模型，返回null）
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误
iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliersfor ( 每个数据集中不属于maybe_inliers的点 ）
if ( 如果点适合于maybe_model，且错误小于t ）
将点添加到consensus_set
if （ consensus_set中的元素数目大于d ）
已经找到了好的模型，现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型，保存该模型直到更好的模型出现
best_model = better_model
best_consensus_set = consensus_set
best_error = this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error
TODO 后续这部分还需要改动
优缺点——
RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。
ransac代码实现： （https://www.cnblogs.com/weizc/p/5257496.html）
#include
#include "LineParamEstimator.h"
LineParamEstimator::LineParamEstimator(double delta) : m_deltaSquared(delta*delta) {}
void LineParamEstimator::estimate(std::vector &data,
std::vector ¶meters)
{
parameters.clear();
if(data.size()<2)
return;
double nx = data[1]->y - data[0]->y;
double ny = data[0]->x - data[1]->x;// 原始直线的斜率为K，则法线的斜率为-1/k
double norm = sqrt(nx*nx + ny*ny);
parameters.push_back(nx/norm);
parameters.push_back(ny/norm);
parameters.push_back(data[0]->x);
parameters.push_back(data[0]->y);
}
void LineParamEstimator::leastSquaresEstimate(std::vector &data,
std::vector ¶meters)
{
double meanX, meanY, nx, ny, norm;
double covMat11, covMat12, covMat21, covMat22; // The entries of the symmetric covarinace matrix
int i, dataSize = data.size();
parameters.clear();
if(data.size()<2)
return;
meanX = meanY = 0.0;
covMat11 = covMat12 = covMat21 = covMat22 = 0;
for(i=0; ix;
meanY +=data[i]->y;
covMat11 +=data[i]->x * data[i]->x;
covMat12 +=data[i]->x * data[i]->y;
covMat22 +=data[i]->y * data[i]->y;
}
meanX/=dataSize;
meanY/=dataSize;
covMat11 -= dataSize*meanX*meanX;
covMat12 -= dataSize*meanX*meanY;
covMat22 -= dataSize*meanY*meanY;
covMat21 = covMat12;
if(covMat11<1e-12) {
nx = 1.0;
ny = 0.0;
}
else { //lamda1 is the largest eigen-value of the covariance matrix
//and is used to compute the eigne-vector corresponding to the smallest
//eigenvalue, which isn't computed explicitly.
double lamda1 = (covMat11 + covMat22 + sqrt((covMat11-covMat22)*(covMat11-covMat22) + 4*covMat12*covMat12)) / 2.0;
nx = -covMat12;
ny = lamda1 - covMat22;
norm = sqrt(nx*nx + ny*ny);
nx/=norm;
ny/=norm;
}
parameters.push_back(nx);
parameters.push_back(ny);
parameters.push_back(meanX);
parameters.push_back(meanY);
}
bool LineParamEstimator::agree(std::vector ¶meters, Point2D &data)
{
double signedDistance = parameters[0]*(data.x-parameters[2]) + parameters[1]*(data.y-parameters[3]);
return ((signedDistance*signedDistance) < m_deltaSquared);
}
template
double Ransac::compute(std::vector ¶meters,
ParameterEsitmator *paramEstimator ,
std::vector &data,
int numForEstimate)
{
std::vector leastSquaresEstimateData;
int numDataObjects = data.size();
int numVotesForBest = -1;
int *arr = new int[numForEstimate];// numForEstimate表示拟合模型所需要的最少点数，对本例的直线来说，该值为2
short *curVotes = new short[numDataObjects]; //one if data[i] agrees with the current model, otherwise zero
short *bestVotes = new short[numDataObjects]; //one if data[i] agrees with the best model, otherwise zero
//there are less data objects than the minimum required for an exact fit
if(numDataObjects < numForEstimate)
return 0;
// 计算所有可能的直线，寻找其中误差最小的解。对于100点的直线拟合来说，大约需要100*99*0.5=4950次运算，复杂度无疑是庞大的。一般采用随机选取子集的方式。
computeAllChoices(paramEstimator,data,numForEstimate,
bestVotes, curVotes, numVotesForBest, 0, data.size(), numForEstimate, 0, arr);
//compute the least squares estimate using the largest sub set
for(int j=0; jleastSquaresEstimate(leastSquaresEstimateData,parameters);
delete [] arr;
delete [] bestVotes;
delete [] curVotes;
return (double)leastSquaresEstimateData.size()/(double)numDataObjects;
}
18. 位姿不同表示间的相互转化、旋转矩阵特征值和特征向量物理意义
19. 真实世界到相机照片的变换可看成射影变换
射影变化是最一般的变换，左上角为可逆矩阵A，右上角为平移t，左小角为缩放aT。右下角v可以变为1，若v不等于0则为0，因此共有15自由度，保持直线性，或理解为接触平面的相交或者相切。
20. 直接法与特征点法的优缺点对比
直接法优势——
1）节省特征提取与匹配的大量时间，易于移植到嵌入式系统中，以及与IMU进行融合；
2）使用的是像素梯度而不必是角点，可以在特征缺失的场合使用，如环境中存在许多重复纹理或是缺乏角点，但出现许多边缘或光线变量不明显区域；
3）可以进行稠密或半稠密的地图重建；
直接法劣势——
1）灰度不变是一个强假设，难以满足（易受曝光和模糊影像）；
2）单像素区没有区分度，需要计算图像块或是相关性；
3）直接法成功的前提，是目标函数从初始值到最优值之间一直是下降的，然而图像非凸。因此需要有一个相当不错的初始估计，还需要一个质量较好的图像；
4）难以实现地图复用、回环检测、丢失后的重定位等：除非存储所有的关键帧图像，否则很难利用先前建好的地图；即使有办法存储所有关键帧的图像，那么在重用地图时，我们还需要对位姿有一个比较准确的初始估计——这通常是困难的。
以下分别为特征法、直接法、光流法对比——
| 优点 |
运动过大时，只要匹配点还在像素内，则不太会引起无匹配，相对于直接法有更好的鲁棒性。 |
只要关键点有梯度即可，可以在渐变的环境下工作 |
不需要计算描述子，不需要匹配特征点，节省了很多计算量。 |
| 不需要计算描述子，不需要匹配特征点，节省了很多计算量。 |
关键点提取的多少基本上都可以工作 |
||
| 可以筹建半稠密乃至稠密的地图 |
从稀疏到稠密重构基本上都可以使用 |
||
| 稀疏的直接法可以做到非常快速的效果，适合real time和资源受限的场合 |
|||
| 缺点 |
特征过多或过少都无法正常工作 |
图像无梯度，则对优化结果无贡献，特别如自动驾驶时候的天空 |
基于灰度不变假设，容易受外界光照的影响。 |
| 只能用来构建稀疏地图 |
基于灰度不变假设，容易受外界光照的影响。 |
相机发生大尺度移动或旋转时无法很好的追踪，非凸优化，容易局部极值。用尺度金字塔改善局部极值，组合光流法（增加旋转描述）改善旋转。 |
|
| 环境特征少，或者提不出角点（如：渐变色）都无法工作 |
相机发生大尺度移动或旋转时无法很好的追踪，非凸优化，容易局部极值。用尺度金字塔改善。 |
||
| 花很多时间在计算描述子和匹配上 |
单个像素没有区分度，需要计算像素块，结果只能少数服从多数。 |
||
| 容易受相机暗角影响 |
21. 常见滤波方法的对比（KF、EKF、IEKF、UKF、PF）
见高博博客： https://www.cnblogs.com/gaoxiang12/p/5560360.html
增加IEKF：
22. 双目测距范围Z=fb/d。问题： 640*480，fov＝90°，zmax＝10m，最小视差为2，求使zmax稳定的最小基线长度（6.25cm）
23. 特征点法与直接法误差模型、Jacobian推导
特征点法的BA——
直接法BA——
hu
注释： 上面这张图片请注意，推导延续了十四讲一书中的公式。但是实际上这样显得有点啰嗦，用到了泰勒展开一阶近似等，其实你完全可以利用链式矩阵求导类似于特征点的BA推导出直接法的BA。 这里省略。
24. 光流的假设、仿射变换、4种方法，svo采取的方法，优势何在
光流假设——
灰度不变性
SVO解读——
参考博客1（SVO解读）： https://www.cnblogs.com/ilekoaiq/p/8659631.html
光流法四种方法——
光流法经典论文： 《Lucas-Kanade 20 Years On: A Unifying Framework》
参考博客2（光流的四种方法）： https://blog.csdn.net/wendox/article/details/52505971
其中SVO才用的是反向复合式 ICIA (Inverse Compositional Image Alignment)
前向与后向的对比——
前向方法对于输入图像进行参数化(包括仿射变换及放射增量). 后向方法则同时参数输入图像和模板图像, 其中输入图像参数化仿射变换, 模板图像参数参数化仿射增量. 因此后向方法的计算量显著降低. 由于图像灰度值和运动参数非线性, 整个优化过程为非线性的.
参数化过程主要要计算: 图像的梯度, 位置对运动参数导数, 运动参数增量. 前向方法中Hessian是运动参数的函数. 提高效率的主要思想是交换模板图像和输入图像的角色.
后向方法在迭代中Hessian是固定的.
前向方法和后向方法在目标函数上不太一样，一个是把运动向量p都是跟着I（被匹配图像），但是前向方法中的迭代的微小量Δp使用I计算的，后向方法中的Δp使用T计算的。因此计算雅克比矩阵的时候，一个的微分在Δp处，而另外一个在0处。所以如果使用雅克比矩阵计算Hessian矩阵，后者计算的结果是固定的。
Compositional 与 Additive对比——
通过增量的表示方式来区分方法. 迭代更新运动参数的时候，如果迭代的结果是在原始的值(6个运动参数)上增加一个微小量，那么称之为Additive，如果在仿射矩阵上乘以一个矩阵(增量运动参数形成的增量仿射矩阵)，这方法称之为Compositional。两者理论上是等效的，而且计算量也差不多。
----------------------------------------------------------
这部分理解有点难度，具体你可以再参考上面的论文以及博客。
25. MSCKF与ROVIO、MSCKF与预积分（structureless factor）
有一篇综述博客不错：
VIO综述 https://blog.csdn.net/xiaoxiaowenqiang/article/details/81192045
这里如果你有时间，先看两篇分析S-MSCKF的文章：
【泡泡读者来稿】一步步深入了解S-MSCKF（一） http://www.sohu.com/a/271224863_715754
【泡泡读者来稿】一步步深入了解S-MSCKF（二） https://www.sohu.com/a/271370131_715754
如果不是很了解VIO， 那先来简单学习一下VIO的知识：
高翔VIO讲解： https://www.jianshu.com/p/23873d04bc60 以及视频： http://www.jintiankansha.me/t/Fseb5PNWJz
【泡泡机器人原创专栏】IMU预积分总结与公式推导（一） https://www.sohu.com/a/242760307_715754
【泡泡机器人原创专栏】IMU预积分总结与公式推导（二） https://www.sohu.com/a/271370131_715754
【泡泡机器人原创专栏】IMU预积分总结与公式推导（三） https://www.sohu.com/a/243601310_715754
【泡泡机器人原创专栏】IMU预积分总结与公式推导（四） http://m.sohu.com/a/244040730_715754
如果你有毅力把上面的内容都看了，那么你已经具备了很好的VIO基础。
剩下的进阶，当然是文献了！！
《On-Manifold Preintegration for Real-Time Visual-Inertial Odometry》
《Quaternion kinematics for the error-state Kalman filter》
《Visual-Inertial Monocular SLAM with Map Reuse》 （VI-ORB）
……
这里就不列了，如果你有志于在VIO方面做出一点小小的科研贡献，那就看经典的开源方案吧： ROVIO， OKIVS， MSCKF，VINS，VIORB 等等。 以上内容，实际上也可以作为VIO的学习路线！
26. 边缘化方式原理
写博不易，您的支持让知识之花绽放得更美丽 ~_~
