Rust机器学习之Linfa
Rust机器学习之Linfa
本文将带领大家用Linfa实现一个完整的Logistics回归,过程中带大家学习Linfa的基本用法。
本文是“Rust替代Python进行机器学习”系列文章的第三篇,其他教程请参考下面表格目录:
| Python库 | Rust替代方案 | 教程 |
|---|---|---|
numpy |
ndarray |
Rust机器学习之ndarray |
pandas |
Polars |
Rust机器学习之Polars |
scikit-learn |
Linfa |
Rust机器学习之Linfa |
pytorch |
tch-rs |
Rust机器学习之tch-rs |
networks |
petgraph |
Rust机器学习之petgraph |
matplotlib |
plotters |
Rust机器学习之plotters |
数据和算法工程师偏爱Jupyter,为了跟Python保持一致的工作环境,文章中的示例都运行在Jupyter上。因此需要各位搭建Rust交互式编程环境(让Rust作为Jupyter的内核运行在Jupyter上),相关教程请参考 《Rust交互式编程环境搭建》。
文章目录
-
- 什么是Linfa
- 逻辑(Logistic)回归
- 用Linfa实现逻辑回归
-
- 安装Linfa
- 加载数据
- 数据探索
- 模型训练
- 模型优化
- 总结
什么是Linfa
Linfa 是一组Rust高级库的集合,提供了常用的数据处理方法和机器学习算法。Linfa对标Python上的scikit-learn,专注于日常机器学习任务常用的预处理任务和经典机器学习算法,目前Linfa已经实现了scikit-learn中的全部算法,这些算法按算法类型组织在各子包中:
| 名字 | 功能 | 状态 | 类别 | 备注 |
|---|---|---|---|---|
| clustering | 数据聚类 | ✅ | 无监督学习 | 用于无标记数据的聚类,包括K-Means、高斯混合模型、DBSCAN和OPTICS等算法 |
| kernel | 用于数据变换的核方法 | ✅ | 预处理 | 将特征向量映射到更高维空间 |
| linear | 线性回归 | ✅ | 部分拟合 | 包含一般最小二乘法(OLS)、广义线性模型(GLM) |
| elasticnet | 弹性网络 | ✅ | 监督学习 | 带有弹性网络约束的线性回归 |
| logistic | 逻辑回归 | ✅ | 部分拟合 | 包含两类逻辑回归模型 |
| reduction | 降维 | ✅ | 预处理 | 扩散映射和主成分分析(PCA) |
| trees | 决策树 | ✅ | 监督学习 | 线性决策树 |
| svm | 支持向量机 | ✅ | 监督学习 | 标记数据集的分类或回归分析 |
| hierarchical | 聚集层次聚类 | ✅ | 无监督学习 | 聚类和构建聚类层次结构 |
| bayes | 朴素贝叶斯 | ✅ | 监督学习 | 包含高斯朴素贝叶斯 |
| ica | 独立成分分析 | ✅ | 无监督学习 | 包含FastICA实现 |
| pls | 偏最小二乘法 | ✅ | 监督学习 | 包含用于降维和回归的PLS估计 |
| tsne | 降维 | ✅ | 无监督学习 | 包含精确解和Barnes-Hut近似t-SNE |
| preprocessing | 标准化和向量化 | ✅ | 预处理 | 包含各种常用数据预处理方法 |
| nn | 最近邻和最小距离 | ✅ | 预处理 | 空间索引结构和距离函数 |
| ftrl | FTRL-Proximal | ✅ | 部分拟合 | 包含L1和L2正则化 |
按类别进行一个分类整理会更清晰:
这些子包几乎涵盖了机器学习所需的所有方面。可以说,Linfa当前最新稳定版0.6.0的功能与scikit-learn完全一致。
逻辑(Logistic)回归
因为本文的重点是如何用Rust解决机器学习问题,所以我们不会深入研究逻辑回归的具体工作原理。然而,我们应该至少对它的含义有一个基本的理解。
逻辑回归是一种统计模型,用于测量结果的概率,如真/假、接受/拒绝等,也可以扩展到多个类别。逻辑回归内部使用logistic函数(也叫S曲线),该函数可以写成:
s ( x ) = 1 1 + e − x s(x) = \frac{1}{1+e^{-x}} s(x)=1+e−x1
这个函数是一个S曲线,得到的结果在0和1之间,x的值越大,s(x)越接近1,x的值越小,s(x)越接近0,具体曲线如下:
Logistic回归的目的是找到与给定数据集拟合最好的函数。简单地说,它模拟了数据中我们关注的随机变量(0或1)的概率。
在机器学习中,通常使用梯度下降来寻找最优模型,这是一种寻找局部最小值的优化方法。目标通常是计算误差,然后将误差最小化。
用Linfa实现逻辑回归
本文的目标是演示如何用Rust构建简单的机器学习应用。为了方便演示和阅读,我们这里使用一个仅包含100条记录的非常小的数据集。
我们还将跳过机器学习的数据准备工作,这里可能包括异常值处理、标准化、数据清洗等预处理步骤。这是数据科学的一个非常重要的部分,但这不在本文的重点,这部分内容大家可以阅读《Rust机器学习之ndarray》 和 《Rust机器学习之Polars》 。
我们使用的数据集和简单,其结构如下:
| score1 | score2 | accepted |
|---|---|---|
| 32.72283304060323 | 43.30717306430063 | 0 |
| 64.0393204150601 | 78.03168802018232 | 1 |
第一列表示学生第一次考试的成绩,第二列表示第二次考试的成绩。这两列是我们数据集的特征;第三列是数据集的目标,表示该学生是否会被学校录取,1表示录取,0表示拒接。
我们机器学习任务的目标是训练一个模型,该模型可以根据两次考试的分数可靠地预测学生是否会被学校录取。我们将数据拆分为训练集和测试集,其中65条数据为训练集,保存在train.csv中;35条数据为测试集,保存在test.csv中。最后,我们将测试训练得到的模型在尚未观测的数据上是否表现良好。
安装Linfa
安装使用Linfa非常简单,只需要在Cargo .toml加入
[dependencies]
linfa = { version = "0.6.0", features = ["openblas-system"] }
linfa-logistic = "0.6.0"
这里我们需要linfa和linfa-logistic两个包,其中linfa提供了基础工具集,linfa-logistic提供了逻辑回归算法。
这里我们还添加了openblas-system特性,让我们的底层计算运行在libopenblas上。Linfa支持多个BLAS/LAPACK后端:
| Linux | macOS | Windows | |
|---|---|---|---|
| OpenBLAS | ✅ | ❌ | ❌ |
| Netlib | ✅ | ❌ | ❌ |
| Intel MKL | ✅ | ✅ | ✅ |
如果你用的操作系统是macOS或Windows,这里请替换成intel-mkl-system。
在机器学习中,我们更喜欢使用Jupyter。如果你已经搭建好Rust交互式编程环境(可以参考 《Rust交互式编程环境搭建》),可以直接通过下面代码引入linfa和linfa-logistic :
:dep linfa = {version="0.6.0", features = ["openblas-system"]}
:dep linfa-logistic = {version="0.6.0"}
除了Linfa外,我们还需要用到ndarray来处理n维向量;用csv和ndarray-csv来加载csv格式的数据。
:dep ndarray = {version = "0.15.6"}
:dep ndarray-csv = {version = "0.5.1"}
:dep csv = {version = "1.1"}
加载数据
任何机器学习的第一步都是载入数据。我们这里也不例外。我们需要从.data/train.csv和.data/test.csv文件中读取数据,并将其转换为ndarray,再用ndarray创建Linfa Dataset。
fn load_data(path: &str) -> Dataset<f64, &'static str, Ix1> {
let mut reader = ReaderBuilder::new()
.has_headers(false)
.delimiter(b',')
.from_path(path)
.expect("can create reader");
let array: Array2<f64> = reader
.deserialize_array2_dynamic()
.expect("can deserialize array");
let (data, targets) = (
array.slice(s![.., 0..2]).to_owned(),
array.column(2).to_owned(),
);
let feature_names = vec!["test 1", "test 2"];
Dataset::new(data, targets).map_targets(|x| {
if *x as usize == 1 {
"accepted"
} else {
"denied"
}
})
.with_feature_names(feature_names)
}
简单解释一下上面的代码。
首先我们用csv::ReaderBuilder读入csv文件。这里的has_headers(false)表示读入的文件没有表头,·.delimiter(b',')表示数据用逗号分隔。
接着用ndarray-csv库提供了deserialize_array2_dynamic()方法可以将csv格式数转换成ndarray::Array2(二维数组)。然后我们将此ndarray二维数组切分成feature和target,我们的数据集中前两列是feature,最后一列是target。
有了feature和target我们就可以用Dataset::new(data, targets)创建Linfa Dataset。Dataset创建好后我们还对里面的数据做了些处理,map_targets中的闭包将target的值映射到字符串(0=“denied”;1=“accepted”),并用with_feature_names对feature字段进行了命名。
最后将创建并处理好的Dataset对象返回给调用者。使用时只需要传入文件路径即可
let train = load_data("data/train.csv");
let test = load_data("data/test.csv");
数据探索
在开始模型训练之前,我们先看一下数据的分布情况。
首先我们将数据分成正例和负例,在可视化时用两种不同颜色来区分两类数据。代码实现上很简单,只需要根据数据集中target的值将数据放入对应类型的列表中即可。代码实现如下:
let mut positive = vec![];
let mut negative = vec![];
let records = train.records().clone().into_raw_vec();
let features: Vec<&[f64]> = records.chunks(2).collect();
let targets = train.targets().clone().into_raw_vec();
for i in 0..features.len() {
let feature = features.get(i).expect("feature exists");
if let Some(&"accepted") = targets.get(i) {
positive.push((feature[0], feature[1]));
} else {
negative.push((feature[0], feature[1]));
}
}
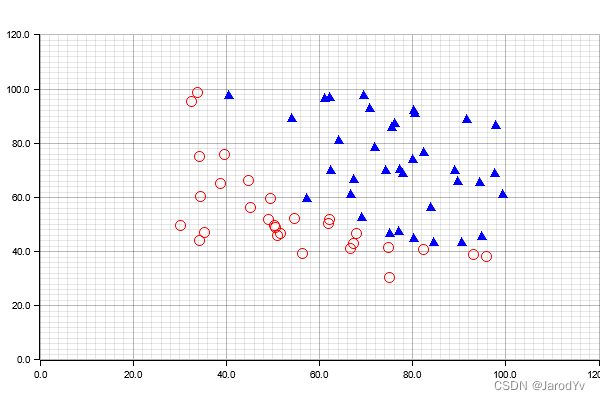
有了数据后,我们用散点图将数据的分布描绘在图上。这里我使用plotters进行绘图,关于如何使用plotters进行数据可视化后面会有专门的教程教大家使用,这里大家先结合注释大体浏览一下代码功能:
:dep plotters = { version = "^0.3.0", default_features = false, features = ["evcxr", "all_series"] }
extern crate plotters;
use plotters::prelude::*;
evcxr_figure((640, 480), |root| {
// 设置图表参数
let mut ctx = ChartBuilder::on(&root)
.set_label_area_size(LabelAreaPosition::Left, 40)// 设置y轴标签区域大小
.set_label_area_size(LabelAreaPosition::Bottom, 40)// 设置x轴标签区域大小
.build_cartesian_2d(0.0..120.0, 0.0..120.0) // 设置直角坐标系的范围
.unwrap();
// 设置网格
ctx.configure_mesh().draw().unwrap();
// 绘制正例散点图
ctx.draw_series(
positive
.iter()
.map(|point| TriangleMarker::new(*point, 5, &BLUE)),
)
.unwrap();
// 绘制负例散点图
ctx.draw_series(
negative
.iter()
.map(|point| Circle::new(*point, 5, &RED)),
)
.unwrap();
Ok(())
})
上代码输出的数据分布如下图:
模型训练
接下来我们正式进入模型构建环节。这个工作可以分为如下几步:
- 构造逻辑回归模型,并用训练集数据进行训练;
- 用测试集数据对训练出的模型进行测试;
- 构建混淆矩阵评估模型在测试集上的精度。
混淆矩阵本质上是一个 2 × 2 2 \times 2 2×2的表,它显示了真阳性(TP)、假阳性(FP)、真阴性(TN)和假阴性(FN),我们可以通过混淆矩阵计算模型的准确率、精确率和召回率等指标。
| 混淆矩阵 | 预测值 | ||
| Positive | Negative | ||
| 真实值 | Positive | TP | FN |
| Negative | FP | TN | |
以上3步Linfa都有封装好的接口可以直接调用。
构造逻辑回归模型
Linfa提供LogisticRegression用于构造逻辑回归模型,下面代码创建逻辑回归模型,并用训练集进行训练:
let model = LogisticRegression::default()
.max_iterations(max_iterations)
.gradient_tolerance(0.0001)
.fit(train)
.expect("can train model");
其中max_iterations()方法用于设置最大迭代次数,gradient_tolerance()用于设置梯度下降的学习率,当变化值小于该值时则停止迭代。调大学习率可以提高算法速度,但是最终得到的可能是局部最优,不是全局最优。
最后,调用.fit(train)开始用传入的训练集训练模型。
测试模型
模型训练好后,可以调用.predict(test)用测试集对模型进行测试:
let validation = model.set_threshold(threshold).predict(test);
这里set_threshold用来设置预测“正”类的概率阈值,默认值为0.5。
创建混淆矩阵
最有一步,我们根据测试的结果构造混淆矩阵。Linfa提供了confusion_matrix方法可以在测试结果上直接生成混淆矩阵:
let confusion_matrix = validation
.confusion_matrix(test)
.expect("can create confusion matrix");
至此,模型训练的核心步骤完成了。接下来我们需要找到训练效果最好的那个模型。
模型优化
上面构造的模型中有2个超参:迭代次数max_iterations 和 决策阈值threshold。我们需要反复多次测试以找到这两个参数的最有值,为此我们需要构造循环多次调用上面的过程。
为了让调用更方便,我们需要先将上面的模型构造和训练过程封装成一个函数,传入训练集、测试集和两个超参,返回混淆矩阵。
fn train_and_test(
train: &DatasetBase<
ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>,
ArrayBase<OwnedRepr<&'static str>, Dim<[usize; 1]>>,
>,
test: &DatasetBase<
ArrayBase<OwnedRepr<f64>, Dim<[usize; 2]>>,
ArrayBase<OwnedRepr<&'static str>, Dim<[usize; 1]>>,
>,
threshold: f64,
max_iterations: u64,
) -> ConfusionMatrix<&'static str> {
let model = LogisticRegression::default()
.max_iterations(max_iterations)
.gradient_tolerance(0.0001)
.fit(train)
.expect("can train model");
let validation = model.set_threshold(threshold).predict(test);
let confusion_matrix = validation
.confusion_matrix(test)
.expect("can create confusion matrix");
confusion_matrix
}
有了上面的函数,我们的循环寻找最优最优超参的代码写起来会很简单:
let mut max_accuracy_confusion_matrix = train_and_test(&train, &test, 0.01, 100);
let mut best_threshold = 0.0;
let mut best_max_iterations = 0;
let mut threshold = 0.02;
for max_iterations in (1000..5000).step_by(500) {
while threshold < 1.0 {
let confusion_matrix = train_and_test(&train, &test, threshold, max_iterations);
if confusion_matrix.accuracy() > max_accuracy_confusion_matrix.accuracy() {
max_accuracy_confusion_matrix = confusion_matrix;
best_threshold = threshold;
best_max_iterations = max_iterations;
}
threshold += 0.01;
}
threshold = 0.02;
}
println!(
"最精确混淆矩阵: {:?}",
max_accuracy_confusion_matrix
);
println!(
"最优迭代次数: {}\n最优决策阈值: {}",
best_max_iterations, best_threshold
);
println!("精确率:\t{}", max_accuracy_confusion_matrix.accuracy(),);
println!("准确率:\t{}", max_accuracy_confusion_matrix.precision(),);
println!("召回率:\t{}", max_accuracy_confusion_matrix.recall(),);
最终经过优化后,最优模型输出如下:
最精确混淆矩阵:
classes | denied | accepted
denied | 11 | 0
accepted | 2 | 22
最优迭代次数: 1000
最优决策阈值: 0.37000000000000016
精确率: 0.94285715
准确率: 0.84615386
召回率: 1
从上面输出我们能看到,只有2个数据分类错误,模型的精确率为94%,模型看起来还不错。
总结
本文中,我们用Linfa训练了一个效果还不错的逻辑回归模型。尽管我们用的数据样本很少,只有100条,但是完整地向大家展示了如何用Linfa进行机器学习。
今天,Rust的机器学习生态已经非常完善,然而社区仍在不断努力,向着Python快速靠近。面向未来,Rust快速、安全的特性会使它成为机器学习领域不可忽视,甚至是主流的编程语言。