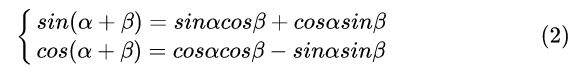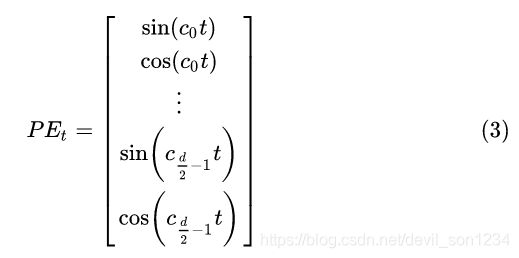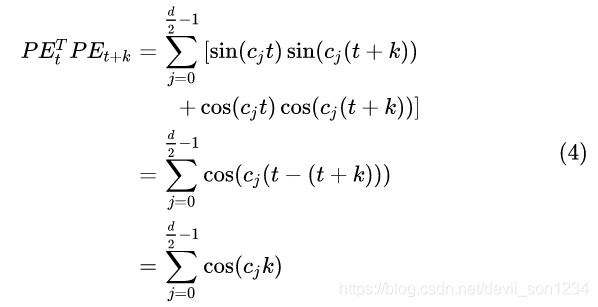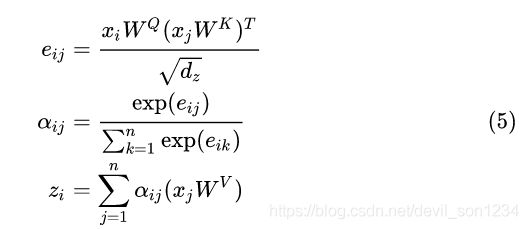【Transformer】浅谈 Transformer-based 模型中的位置表示
本文小结：本文主要对原始 Transformer[1]、RPR[2]以及 Transformer-XL[3] 中使用的位置表示方法，进行详细介绍。从最初的绝对位置编码，与单词嵌入相加作为第一层的输入，再到 RPR 提出直接在注意力分数的计算中引入相对位置信息，并学习相对距离的表示矩阵(长度固定)，再到 Transformer-XL 中引入偏置信息，并重新使用 Transformer 中的编码公式生成相对距离的表示矩阵，使长度可泛化。
0. 位置信息
首先简单谈一下位置信息。一般将位置信息简单分为绝对位置信息和相对位置信息，并且前者对句子语义的影响不大，更为重要的是后者。
以情感分析 sentiment analysis 为例：
- I like this movie because it doesn't have an overhead history.
Positive - I don'tlike this movie because it has an overhead history.
Negative
don’t 与like的相对位置不同，决定了这两句话的情感取向是一正一负的，但在传统词袋(Bag-Of-Words BOW)模型中，这两句话得到的句子表征却是一致的，可见单词的相对位置对语义有关键性影响。
再以命名实体识别 Named Entity Recognition 为例[4]：
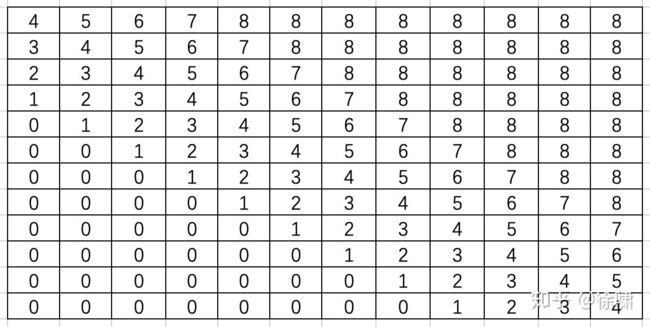
一般而言，在 Inc. 之前的单词为 ORG 而在 in 之后为 TIME 或 LOC ，但是同为 Louis Vuitton ，与 Inc. 相距较远的为PER，指的是创立者(人)这一实体，而相距较近的为ORG，指的是组织(公司)这一实体。可见，单词之间的相对位置在 NER 任务中是十分重要的。
需要注意的是，相对位置是具有方向性的(Inc. 与 in 的相对距离为 -1，1854 与 in 的相对距离为 1)
那么，如何对位置信息进行表示呢？
感兴趣的同学可以看下这篇文章 Encoding Word Order in Complex Embeddings 。
下文结合原始 Transformer，RPR，Transformer-XL 以及相关变体，试解释 Transformer-based 模型中的位置信息的表示问题。
1. 原始 Transformer [1]
原始 Transformer 中使用 Positional Encoding 生成固定的位置表示。
其中，pos 指的是 token 的位置。设句子长度为 
，那么 
。i 是向量的某一维度，例如 
时，
。
因此，借助上述正余弦公式，我们可以为每个位置生成 
维的位置向量。为什么会选择如上公式呢？作者表示：
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k,
can be represented as a linear function of
已知三角函数公式如下：
因此，可以将 可以表示为 
的线性表示如下：
作者希望借助上述绝对位置的编码公式，让模型能够学习到相对位置信息。
虽然如此获得的 position embeddings，两者之间的点积能够反应相对距离，但它缺乏方向性，并且这种特性(相对距离)会被原始 Transformer 的注意力机制破坏：[4]
基于公式 
，位置 t 的位置嵌入可以表示为：
其中， 
表示位置嵌入的维度， 
表示由 
决定的常量
，由
可推得：
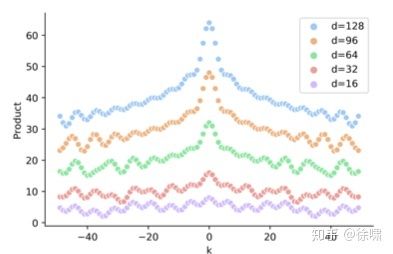
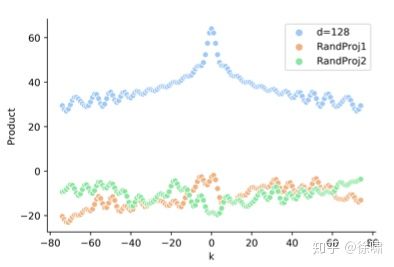
因此，对于给定的位置 pos 和 偏移量 k 而言，
只取决于偏移量 k，因此两者的点积可以反映相对距离 k。如上图所示，点积的结果是对称的，并且随
增加而减少(但并不单调)。
此外，由于点积结果只依赖于 k，那么令 
，有 
对于给定的位置 pos 和 偏移量 k 而言，
，即两者的点积无法反映方向性。
但是在 Transformer 中，由于需要经过映射，即两者间的点积实际是 
并可以视为
，然而如上图所示，此时并没有看到相对距离 k 的清晰模式。
最后，Transformer 之前的《Convolutional Sequence to Sequence Learning》[5] 以及之后的 BERT[6] 都没有选择使用 Positional Encoding 的方式生成位置表示，而是采取了所谓的“learned and fixed”的可学习的 Position embedding ，也就是去训练一个嵌入矩阵，大小为 
，这里暂且按下不表。
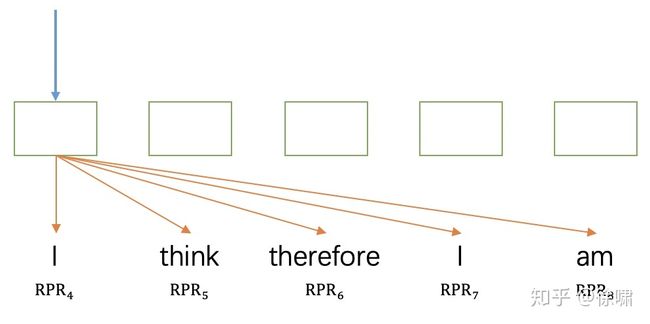
2. 相对位置表示[2]
Relative Position Representations(以下简称为RPR) 一文中认为，RNN 通常依靠其循环机制，结合
时刻的输入和前一时刻的隐层状态
计算出
，直接通过其顺序结构沿时间维度捕获相对和绝对位置。而非 RNN 模型不需要顺序处理输入，则需要显式编码才能引入位置信息。
Transformer 中的 Self-attention 机制如下，输入 
，输出 
：
3. Transformer-XL[3]
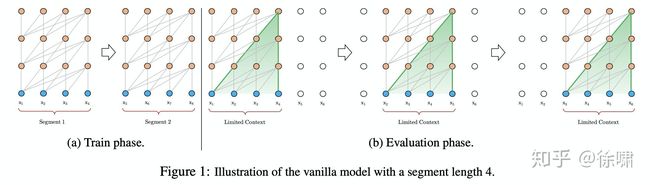
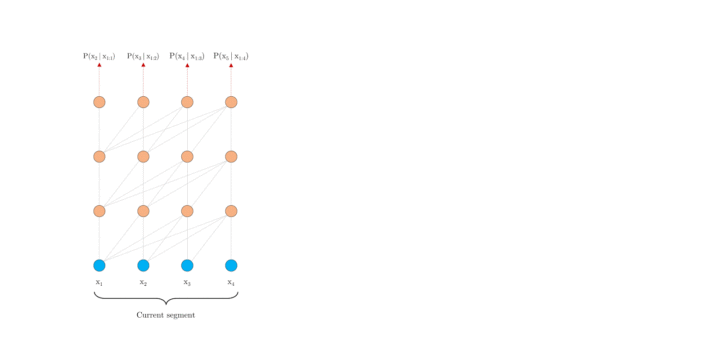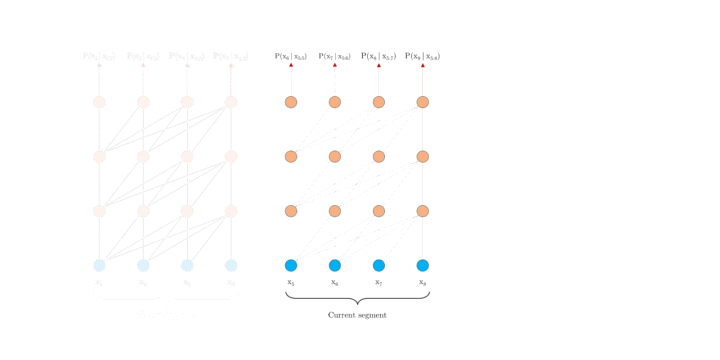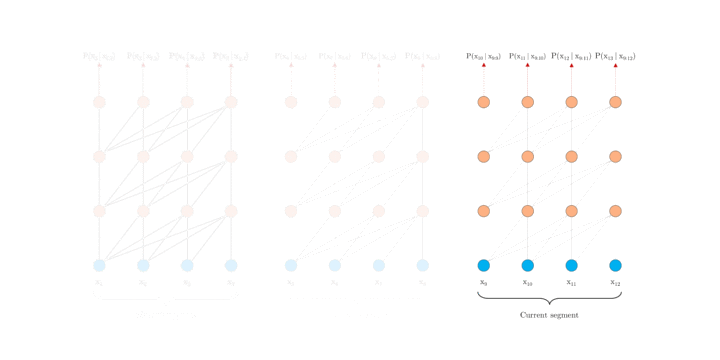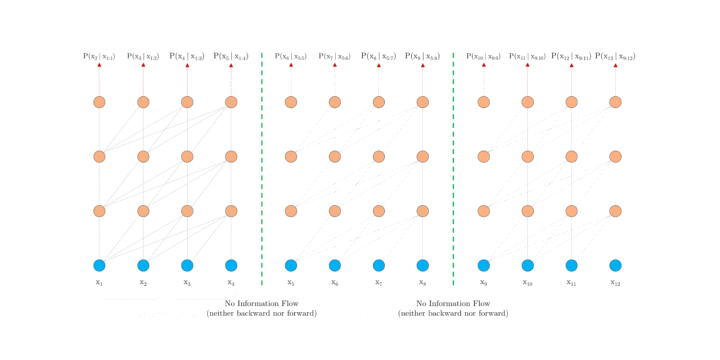
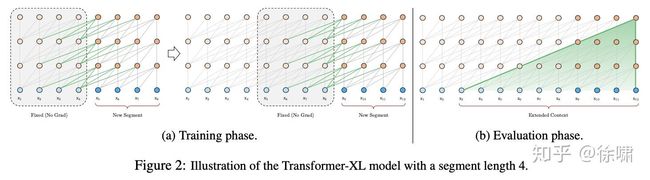
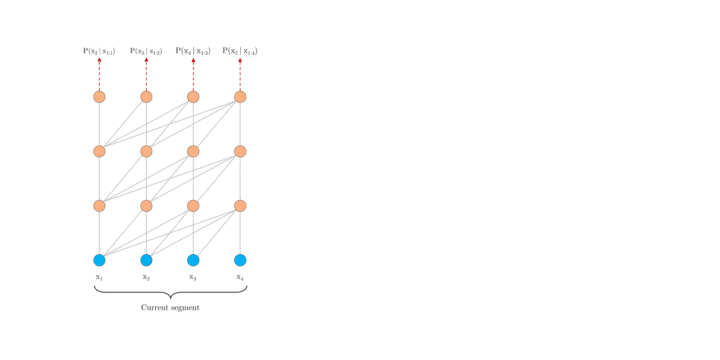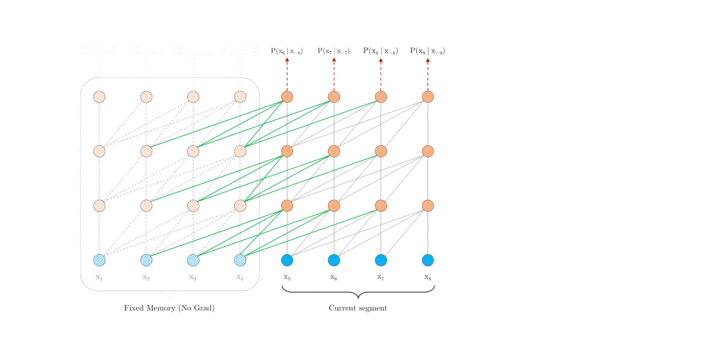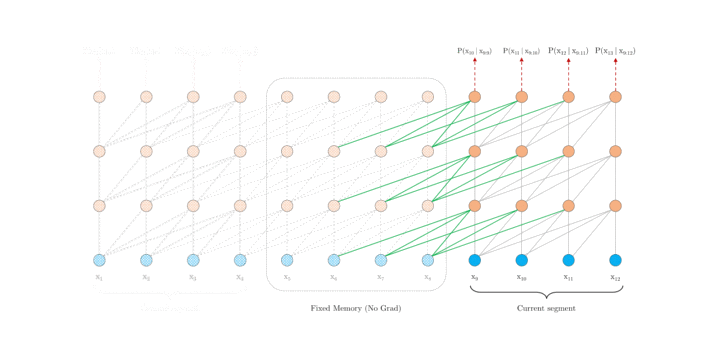
首先深入探究 Al-Rfou 等人的做法，下文将其称为 vanilla model。如上图 1.a 所示， vanilla model 将整个语料库拆分为长度受限的片段，并且只在每个片段内训练模型，忽略了来自先前片段的所有上下文信息。这使得训练过程中，信息不会在 forward 或 backward 过程中跨片段流动，而且这使得最大依赖长度受到了片段长度的限制(这本是 Self-attention 的优势)。其次，虽然可以通过 padding 来考虑句子边界或任何其他语义边界，但是在实践中直接简单分块已成为提高效率的标准做法。这也就是作者说的上下文碎片问题。
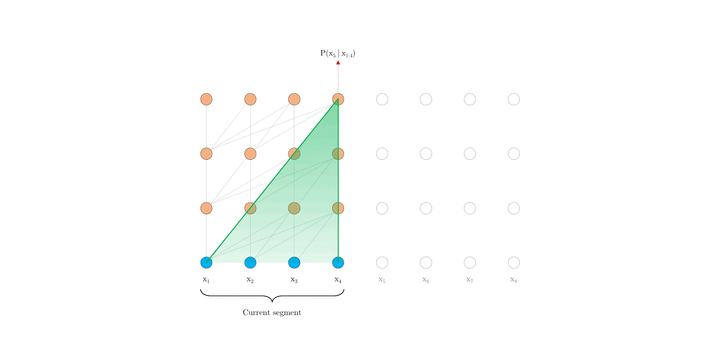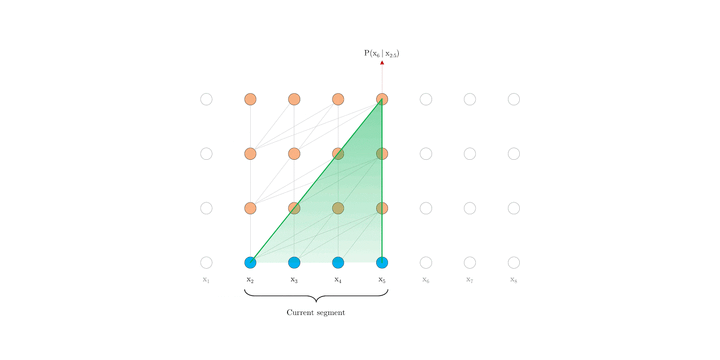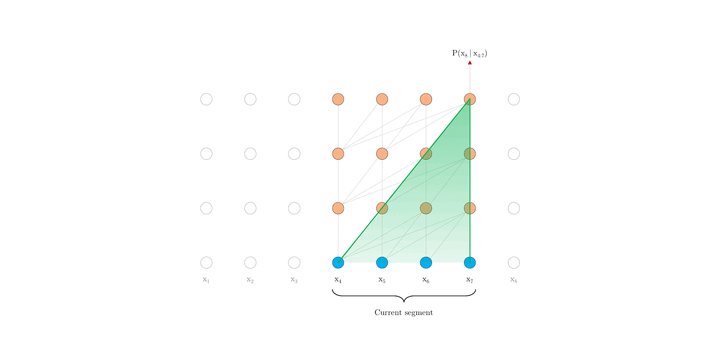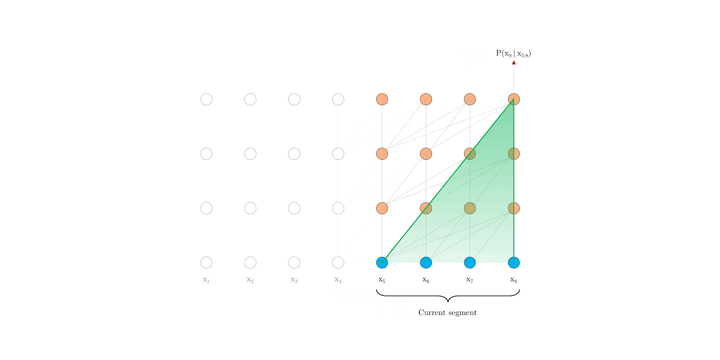
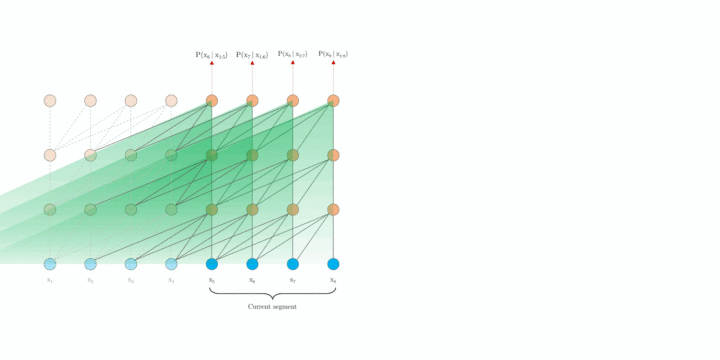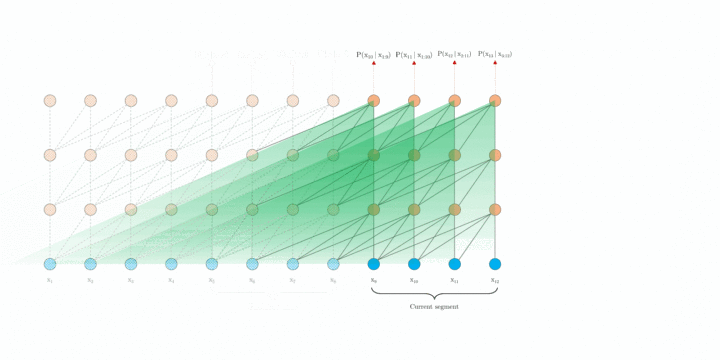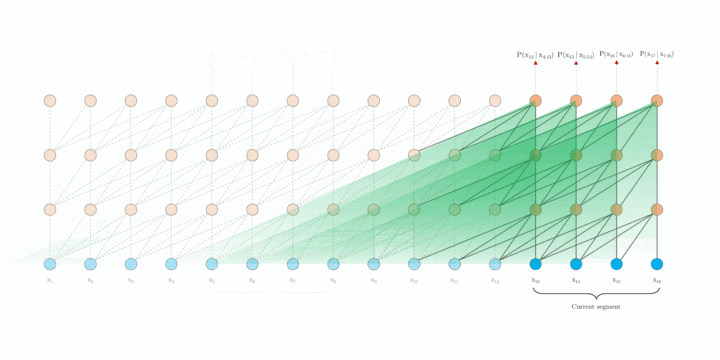
在评估过程中，vanilla model 也在每一步中消耗与训练中相同长度片段，但仅在最后一个位置进行预测。 然后，在下一步仅将片段向右移动一个位置，并且重新进行计算。如图 1.b 所示，如此可确保每一步预测都能利用训练期间暴露的最长可能上下文，并且还缓解了训练中遇到的上下文碎片问题。 但是，这种评估过程太过昂贵。
这里我们先来看 XL 中的片段循环机制。引入循环机制，在训练过程中，前一片段中的隐藏状态序列(每一层都)会被固定并缓存，以便在处理下一片段时使用其作为「扩展上下文」。如图 2.a 所示，绿色部分表示当前片段使用的扩展上下文。对于每一层而言，输入为前一片段以及当前片段的前一层的输出，从而可以保证对长期依赖的建模能力并避免了上下文碎片问题。
参考
- ^abAttention Is All You Need https://arxiv.org/abs/1706.03762
- ^abSelf-Attention with Relative Position Representations https://arxiv.org/abs/1803.02155
- ^abTransformer-XL: Attentive Language Models Beyond a Fixed-Length Context https://arxiv.org/abs/1901.02860
- ^abcTENER: Adapting Transformer Encoder for Name Entity Recognition https://arxiv.org/abs/1911.04474
- ^Convolutional Sequence to Sequence Learning https://arxiv.org/abs/1705.03122
- ^BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding https://arxiv.org/abs/1810.04805
- ^How self-attention with relative position representations works https://medium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245a
- ^Character-Level Language Modeling with Deeper Self-Attention https://arxiv.org/abs/1808.04444
- ^Google AI Blog https://ai.googleblog.com/2019/01/transformer-xl-unleashing-potential-of.html