NLP位置编码
NLP位置编码
- Learned Positional Embedding
- Sinusoidal Position Embedding
- Relative Position Representations
-
- 实验结果
- Transfomer-XL中的相对位置编码
-
- 实验结果
- Complex Embeddings
-
- 实验结果
- 位置特征与内容特征间的关系
-
- 去掉内容特征
- 将embedding相加改为拼接
- 拆分位置特征和内容特征
- 在测试时分别disable位置特征和内容特征
以Transfomer和Bert为首的一系列深度模型不断验证着Attention模式在NLP领域的成功。Attention模式与传统的RNN模式相比,优点确实很多。比如不受长距离约束,可以并行化加快速度等等。
一般来说,一个自然语言的句子,它所携带的信息 = 组成句子的词的信息 + 语法(or 语序)信息。
RNN看似只处理了词语的信息,但其实它是通过顺序输入的方式得到了词语间的语序信息,这种方式是优点是自然,不需要其他人工干预;但缺点是无法掌控获得的语序信息,而且RNN受长距离约束和难以并行等问题也是由顺序输入带来的。
Attention则摒弃了原始句子的自然语序,不同词间的信息交互不受自然语序的影响。但直接抛弃语序信息在很多任务里是不可取的,例如翻译任务,情感分类任务等。因此大部分采用Attention思想的模型需要配一个“位置编码”来保留句子的语序信息,这篇文章我们就来介绍一些比较常用的位置编码方式。
Learned Positional Embedding
BERT中使用的位置编码,随机初始化position embedding,然后随着模型训练得到更新。
优点:简单方便,无需额外开销
缺点:1.这样得到的位置编码是独立训练得到的,不同位置的编码向量没有明显的约束关系,因此只能建模绝对位置信息,不能建模不同位置之间的相对关系。
2.句子长度不能超出位置编码的范围
- 词向量里面的: man - women = king - queen 是怎么来的?是否一定存在这样的关系?其他词也适用吗?
- learned positional embedding 是否也有这样的关系?否,词向量建模的是语义,因此词向量间在语义上是有相关性的,但learned positional embedding建模的是{1,2,3…}并且没有给定任何约束关系,所以其实是完全独立训练的。
Sinusoidal Position Embedding
这是Transformer模型里用到的位置编码模式,对每一个位置 p o s pos pos,它的位置编码是:
P E ( p o s , 2 i ) = s i n ( p o s 1000 0 2 i d m o d e l ) P E ( p o s , 2 i + 1 ) = c o s ( p o s 1000 0 2 i d m o d e l ) \begin{aligned} PE(pos,2i) & = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})\\ PE(pos,2i+1) & = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \end{aligned} PE(pos,2i)PE(pos,2i+1)=sin(10000dmodel2ipos)=cos(10000dmodel2ipos)
首先我们注意到由于它的定义方式,可得:
P E ( p o s + k , 2 i ) = P E ( p o s , 2 i ) P E ( k , 2 i + 1 ) + P E ( p o s , 2 i + 1 ) P E ( k , 2 i ) P E ( p o s + k , 2 i + 1 ) = P E ( p o s , 2 i + 1 ) P E ( k , 2 i + 1 ) − P E ( p o s , 2 i ) P E ( k , 2 i ) \begin{aligned} PE(pos+k,2i) &= PE(pos,2i)PE(k,2i+1)+PE(pos,2i+1)PE(k,2i)\\ PE(pos+k,2i+1) & =PE(pos,2i+1)PE(k,2i+1)-PE(pos,2i)PE(k,2i) \end{aligned} PE(pos+k,2i)PE(pos+k,2i+1)=PE(pos,2i)PE(k,2i+1)+PE(pos,2i+1)PE(k,2i)=PE(pos,2i+1)PE(k,2i+1)−PE(pos,2i)PE(k,2i)
重新记 P E ( k , 2 i ) = u ( k ) , P E ( k , 2 i + 1 ) = v ( k ) PE(k,2i) = u(k),PE(k,2i+1) = v(k) PE(k,2i)=u(k),PE(k,2i+1)=v(k),那么:
[ P E ( p o s + k , 2 i ) P E ( p o s + k , 2 i + 1 ) ] = [ v ( k ) u ( k ) − u ( k ) v ( k ) ] [ P E ( p o s , 2 i ) P E ( p o s , 2 i + 1 ) ] \left[ \begin{matrix} PE(pos+k,2i) \\ PE(pos+k,2i+1) \end{matrix} \right] = \left[ \begin{matrix} v(k) & u(k) \\ -u(k) & v(k) \end{matrix} \right] \left[ \begin{matrix} PE(pos,2i) \\ PE(pos,2i+1) \end{matrix} \right] [PE(pos+k,2i)PE(pos+k,2i+1)]=[v(k)−u(k)u(k)v(k)][PE(pos,2i)PE(pos,2i+1)]
即给定相对位移k,PE(pos+k)可以用PE(pos)的线性表示。
此外,根据Attention的计算方式, p o s 1 pos_1 pos1和 p o s 2 pos_2 pos2这两个位置的相关性由 P E ( p o s 1 ) T ∗ P E ( p o s 2 ) PE(pos_1)^T*PE(pos_2) PE(pos1)T∗PE(pos2)描述:
P E ( p o s 1 ) T ∗ P E ( p o s 2 ) = ∑ i = 1 d 2 − 1 s i n ( p o s 1 1000 0 2 i d ) ∗ s i n ( p o s 2 1000 0 2 i d ) + c o s ( p o s 1 1000 0 2 i d ) ∗ c o s ( p o s 2 1000 0 2 i d ) = ∑ i = 1 d 2 − 1 c o s ( p o s 1 − p o s 2 1000 0 2 i d ) \begin{aligned} PE(pos_1)^T*PE(pos_2) &= \sum_{i=1}^{\frac{d}{2}-1} sin(\frac{pos_1}{10000^{\frac{2i}{d}}})*sin(\frac{pos_2}{10000^{\frac{2i}{d}}})+ cos(\frac{pos_1}{10000^{\frac{2i}{d}}})*cos(\frac{pos_2}{10000^{\frac{2i}{d}}}) \\ &= \sum_{i=1}^{\frac{d}{2}-1} cos(\frac{pos_1-pos_2}{10000^{\frac{2i}{d}}}) \end{aligned} PE(pos1)T∗PE(pos2)=i=1∑2d−1sin(10000d2ipos1)∗sin(10000d2ipos2)+cos(10000d2ipos1)∗cos(10000d2ipos2)=i=1∑2d−1cos(10000d2ipos1−pos2)
下图是不同d(位置编码向量长度)下, P E ( p o s 1 ) T ∗ P E ( p o s 2 ) PE(pos_1)^T*PE(pos_2) PE(pos1)T∗PE(pos2) 关于 p o s 1 − p o s 2 pos_1-pos_2 pos1−pos2的图像:

但这个的问题首先在于, c o s cos cos是一个偶函数,也就是说 p o s 1 − p o s 2 pos_1-pos2 pos1−pos2等于 a a a或 − a -a −a对位置相关性是没有影响的,但实际上,我们希望位置编码是可以区分前后的。
第二,在实际的Transfomer Attention计算中,input embedding首先需要经过一个线性映射:
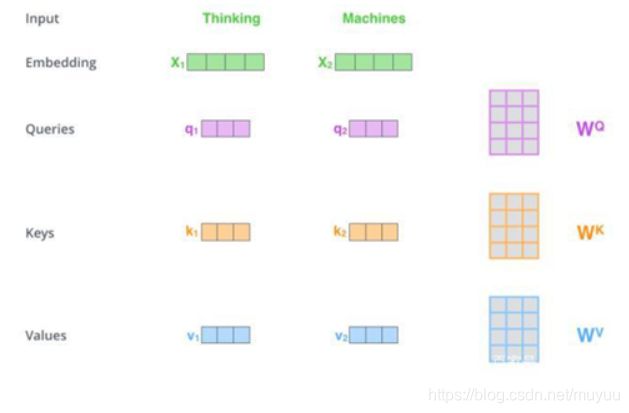
因此真正使用的并不是 P E 1 T P E 2 PE_1^TPE_2 PE1TPE2,而是 P E 1 T W Q T W K P E 2 PE_1^TW_Q^TW_KPE_2 PE1TWQTWKPE2。初始化时 W Q , W K W_Q,W_K WQ,WK均是随机初始化的,所以 P E 1 T W Q T W K P E 2 PE_1^TW_Q^TW_KPE_2 PE1TWQTWKPE2大概是:

注: 观察到 P E 1 PE_1 PE1和 P E 2 PE_2 PE2的每个值是在[-1,1]之间,因此把随机矩阵的值也取在[-1,1]
可以发现当线性变换矩阵是随机初始化时, P E 1 T W Q T W K P E 2 PE_1^TW_Q^TW_KPE_2 PE1TWQTWKPE2就跟 p o s 1 − p o s 2 pos_1-pos_2 pos1−pos2没有了清晰的相关性。
Note:使用Sinusoidal Position Embedding和Learned Positional Embedding在实验表现上区别不大,因此后面的一些论文如BERT,处于简便性考虑,采用的是Learned Positional Embedding
- 随着Transfomer模型的训练,这一现象会不会有所改善?
- 增加约束 W Q T W K = I W_Q^TW_K = I WQTWK=I,是否可以在解决上述问题时,不影响模型其他方面的效果?
- embeding 中的参数为什么取10000?
Relative Position Representations
Paper: Self-Attention with Relative Position Representations (Shaw et al.2018)
Transformer中的Self-attention可以记作:
e i j = x i W Q ( x j W K ) T d z α i j = e x p ( e i j ) ∑ k = 1 n e x p ( e i k ) z i = ∑ j = 1 n α i j ( x j W V ) \begin{aligned} e_{ij} &= \frac{x_iW^Q(x_jW^K)^T}{\sqrt{d_z}}\\ \alpha_{ij} & = \frac{exp(e_{ij})}{\sum_{k=1}^n exp(e_{ik})}\\ z_i & = \sum_{j=1}^n \alpha_{ij}(x_jW^V) \end{aligned} eijαijzi=dzxiWQ(xjWK)T=∑k=1nexp(eik)exp(eij)=j=1∑nαij(xjWV)
由于上面提到的Sinusoidal Position Embedding会被后面隐藏层的线性变化扰乱其与相对位置的关系,因此一个自然的想法是在每个隐藏层都再加上相对位置编码的信息。因此Transfomer的研究人员又提出了Relative Position Representations(以下简称RPR),在其中设计了一个 Relative embedding table(假设句子长度为6):
( u 0 u 1 u 2 u 3 u 3 u 3 u − 1 u 0 u 1 u 2 u 3 u 3 u − 2 u − 1 u 0 u 1 u 2 u 3 u − 3 u − 2 u − 1 u 0 u 1 u 2 u − 3 u − 3 u − 2 u − 1 u 0 u 1 u − 3 u − 3 u − 3 u − 2 u − 1 u 0 ) \begin{pmatrix} u_0&u_1&u_2&u_3&u_3&u_3\\ u_{-1}&u_0&u_1&u_2&u_3&u_3\\ u_{-2}&u_{-1}&u_0&u_1&u_2&u_3\\ u_{-3}&u_{-2}&u_{-1}&u_0&u_1&u_2\\ u_{-3}&u_{-3}&u_{-2}&u_{-1}&u_0&u_1\\ u_{-3}&u_{-3}&u_{-3}&u_{-2}&u_{-1}&u_0 \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎛u0u−1u−2u−3u−3u−3u1u0u−1u−2u−3u−3u2u1u0u−1u−2u−3u3u2u1u0u−1u−2u3u3u2u1u0u−1u3u3u3u2u1u0⎠⎟⎟⎟⎟⎟⎟⎞
将这个Relative embedding table记作 { a i j K } \{a^K_{ij}\} {aijK},其中每个 u i u_i ui都是d维向量,那么带RPR的Self-attention变为:
e i j = x i W Q ( x j W K + a i j K ) T d z α i j = e x p ( e i j ) ∑ k = 1 n e x p ( e i k ) z i = ∑ j = 1 n α i j ( x j W V + a i j V ) \begin{aligned} e_{ij} &= \frac{x_iW^Q(x_jW^K+ \textcolor{red}{a_{ij}^K} )^T}{\sqrt{d_z}}\\ \alpha_{ij} & = \frac{exp(e_{ij})}{\sum_{k=1}^n exp(e_{ik})}\\ z_i & = \sum_{j=1}^n \alpha_{ij}(x_jW^V + \textcolor{red}{a_{ij}^V}) \end{aligned} eijαijzi=dzxiWQ(xjWK+aijK)T=∑k=1nexp(eik)exp(eij)=j=1∑nαij(xjWV+aijV)
其中 { a i j V } \{a^V_{ij}\} {aijV}也是一个跟 { a i j K } \{a^K_{ij}\} {aijK}形状一样的table。
结合公式不难发现, { a i j K } \{a^K_{ij}\} {aijK}和 { a i j V } \{a^V_{ij}\} {aijV}的目的就是分别在计算 e i j e_{ij} eij和 z i z_i zi的时候加上一个相对位置量,比如对于句子“我喜欢吃苹果”,那么“吃”对于“我”的相对位置量就是 a 1 , 4 K = u 3 a^K_{1,4}=u_3 a1,4K=u3,"喜"对于"欢"的相对位置量就是 a 3 , 2 K = u − 1 a_{3,2}^K=u_{-1} a3,2K=u−1。论文设计的这个Relative embedding table其实就是要保证相对距离相同的两个位置间的相对位置量是一样的,在这个基础上矩阵 { a i j K } \{a^K_{ij}\} {aijK}和 { a i j V } \{a^V_{ij}\} {aijV}都是可以跟随模型训练而更新的。
而且论文还作了一个假设(后由实验验证),设置一个超参k,当相对距离大于k之后,就认为相对位置量不再随着相对距离的增大而变化,而是统一设为 u k u_k uk或者 u − k u_{-k} u−k。
最后不同的Head之间的Relative embedding table是共享的,因此每一层的位置编码参数只有 ( 2 k + 1 ) × d × 2 (2k+1)\times d \times 2 (2k+1)×d×2个。
##########################################################################################
与Sinusoidal Position Embedding比较
- 正余弦编码仅加在了embedding层,而如上面所论证的,初始的位置编码会在后面被线性变换所干扰。而RPR是在每一层计算attention时都加上了relative position embedding
- 其“缺点”是超出截断距离的相对位置量不再变化(受限于它的定义),而正余弦编码的好处正是不受限于相对位置的大小
##########################################################################################
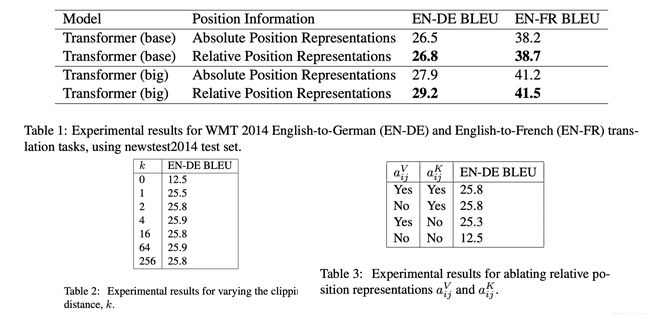
实验结果
- 在 WMT14 英德数据集上 base model BLEU 提升了 0.3, big model 提升了 1.3
- Ablation 实验中,改变最大位置距离 k,显示 k 从 0-4 增大的过程 performance 有明显的提升,之后再增大 k 提升不明显
- Attention bias 中的相对项提高更多的 performance, 而 SoftMax 之后再 Value 上加的那个相对项提升的性能略少
Transfomer-XL中的相对位置编码
Paper: Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context(2019)
由于RPR的实验表明Value上加的相对位置编码对实验结果影响不大。因此Transfomer_XL中就直接放弃了对Value项的修改,而是专注于Attention Bias项:
e i j ^ = ( x i + p i ) W Q W K T ( x j + p j ) = x i W Q W K T x j + x i W Q W K T p j + p i W Q W K T x j + p i W Q W K T p j → x i W Q W K , E T x j + x i W Q W K , R T R i − j + u W K , E T x j + v W K , R T R i − j \begin{aligned} \hat{e_{ij}} &= (x_i + p_i) W_QW_K^T (x_j + p_j)\\ & = x_i W_QW_K^T x_j + x_i W_QW_K^T p_j + p_i W_QW_K^T x_j + p_i W_QW_K^T p_j \\ & \rightarrow x_i W_Q\textcolor{green}{W_{K,E}}^T x_j + x_i W_Q\textcolor{green}{W_{K,R}}^T \textcolor{blue}{R_{i-j}} + \textcolor{red}{u}\textcolor{green}{W_{K,E}}^T x_j + \textcolor{red}{v}\textcolor{green}{W_{K,R}}^T \textcolor{blue}{R_{i-j}} \end{aligned} eij^=(xi+pi)WQWKT(xj+pj)=xiWQWKTxj+xiWQWKTpj+piWQWKTxj+piWQWKTpj→xiWQWK,ETxj+xiWQWK,RTRi−j+uWK,ETxj+vWK,RTRi−j
其中 x i x_i xi和 p i p_i pi分别是词向量和位置编码。
Transfomer-XL中对上式做了以下修改:
- 将绝对位置编码 p j p_j pj改为相对位置编码 R i − j R_{i-j} Ri−j,其中 R i − j R_{i-j} Ri−j是固定的不可训练量,其定义同正余弦编码
- 由于已经将绝对位置编码 p j p_j pj改成了相对位置量 R i − j R_{i-j} Ri−j,因此绝对位置量 p i p_i pi需要保证对所有其他位置来说是不变的,因此将第三项里面的 p i W Q p_iW_Q piWQ整体替换成一个可训练量 u u u(因为 W Q W_Q WQ是可训练的)。同理将第四项里的 p i W Q p_iW_Q piWQ也替换成一个可训练量 v v v
- 将key的embedding和positional encoding 分别采用了不同的线性变换。其中 W K , E W_{K,E} WK,E对应于key的embedding的线性映射矩阵, W K , R W_{K,R} WK,R对应与key的positional encoding的线性映射矩阵。
这样的得到的Attention Bias项具有了很好的解释性:
- 第一项 x i W Q W K , E T x j x_i W_Q\textcolor{green}{W_{K,E}}^T x_j xiWQWK,ETxj,表示内容偏差
- 第二项 x i W Q W K , R T R i − j x_i W_Q\textcolor{green}{W_{K,R}}^T \textcolor{blue}{R_{i-j}} xiWQWK,RTRi−j,表示基于内容的位置偏差
- 第三项 u W K , E T x j \textcolor{red}{u}\textcolor{green}{W_{K,E}}^T x_j uWK,ETxj,表示基于位置的内容偏差
- 第四项 v W K , R T R i − j \textcolor{red}{v}\textcolor{green}{W_{K,R}}^T \textcolor{blue}{R_{i-j}} vWK,RTRi−j, 表示位置偏差
与RPR的比较
将RPR的公式展开
e i j ^ = x i W Q ( x j W K + a i j K ) T = x i W Q W K T x j + x i W Q a i j K T \begin{aligned} \hat{e_{ij}} = x_iW^Q(x_jW^K+ \textcolor{red}{a_{ij}^K} )^T = x_i W_QW_K^T x_j + x_i W_Q\textcolor{red}{a_{ij}^K} ^T \end{aligned} eij^=xiWQ(xjWK+aijK)T=xiWQWKTxj+xiWQaijKT
只对应了Transfomer-XL中的第一项和第二项,所以Transfomer-XL中的位置编码可以说是RPR的拓展。而且Transfomer-XL使用了正余弦编码来表示相对位置量,因此它是不受限于数据长短的,而RPR中长度超过一定位置就只能截断。
##########################################################################################
实验结果
比较了原版Transformer和Transformer-XL,采用不同position encoding方式。
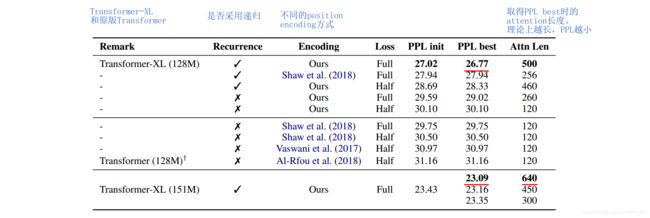
保证模型大小一致的前提下,Transformer-XL在采用自己的位置编码时,比采用RPR的位置编码,PPL减小了1.2
Complex Embeddings
Paper: Encoding word order in complex embeddings (2020)
前面几种位置编码方式依然是在“词向量+位置向量”的范畴里面探索位置向量可能的形式,而这篇论文直接跳出了这个框架,提出了一个全新的假设:
记一个单词在词表里的索引为 j j j,它在文章里的位置是 p o s pos pos。那么上面的对词向量和位置向量的表达方式可以记作:
f ( j , p o s ) = f w e ( j ) + f p e ( p o s ) f(j,pos) = f_{we}(j) + f_{pe}(pos) f(j,pos)=fwe(j)+fpe(pos)
其中 f w e , f p e : N → R D f_{we}, f_{pe} : \mathbb{N} \rightarrow \mathbb{R}^D fwe,fpe:N→RD
而Complex Embeddings里把 f ( j , p o s ) f(j,pos) f(j,pos)拓展为一个光滑的二元函数: f ( j , p o s ) = g j ( p o s ) ∈ C D f(j,pos) = g_{j}(pos) \in \mathbb{C}^D f(j,pos)=gj(pos)∈CD,展开变成:
[ g j , 1 ( p o s ) , ⋯ , g j , D ( p o s ) ] ∈ C D [g_{j,1}(pos),\cdots,g_{j,D}(pos) ] \in \mathbb{C}^D [gj,1(pos),⋯,gj,D(pos)]∈CD
下面将 g j , d g_{j,d} gj,d简记为g,因此 g : N → C g: \mathbb{N} \rightarrow \mathbb{C} g:N→C是关于位置 p o s pos pos的函数。
为了使得 g g g能够体现位置间的相对关系,对任意 n ∈ N n \in \mathbb{N} n∈N我们希望存在一个函数 T n : C → C T_n: \mathbb{C} \rightarrow \mathbb{C} Tn:C→C 满足
g ( p o s + n ) = T n ( g ( p o s ) ) g(pos+n) = T_n(g(pos)) g(pos+n)=Tn(g(pos))
也就是说 g ( p o s + n ) g(pos+n) g(pos+n)可用 g ( p o s ) g(pos) g(pos)和 n n n来表示。论文中为了简化问题,将 T n T_n Tn限定为线性变换,i.e. 存在一个函数 w : N → C w: \mathbb{N} \rightarrow \mathbb{C} w:N→C,满足 ∀ n , T n ( g ( p o s ) ) = T ( n , g ( p o s ) ) = w ( n ) g ( p o s ) \forall n, T_n(g(pos)) = T(n,g(pos)) = w(n)g(pos) ∀n,Tn(g(pos))=T(n,g(pos))=w(n)g(pos)。以上性质被称为Position-free offset transformation
第二个性质比较trivial,要求 g g g是有界的,i.e. ∃ δ > 0 , 对 ∀ p o s , 有 ∣ g ( p o s ) ∣ ≤ δ \exists \delta > 0, 对\forall pos, 有|g(pos)| \le \delta ∃δ>0,对∀pos,有∣g(pos)∣≤δ
接下来论文给出了一个满足以上两个性质的 g ( p o s ) g(pos) g(pos)的等价形式:
g ( p o s ) = z 2 z 1 p o s z 1 , z 2 ∈ C , ∣ z 1 ∣ ≤ 1 g(pos) = z_2 z_1^{pos} \quad z_1,z_2 \in \mathbb{C} , |z_1|\le 1 g(pos)=z2z1posz1,z2∈C,∣z1∣≤1
##########################################################################################
proof: 充分性,由于 g g g满足Position-free offset transformation性质, ∀ n 1 , n 2 ∈ N \forall n_1, n_2\in \mathbb{N} ∀n1,n2∈N
w ( n 1 ) w ( n 2 ) g ( p o s ) = w ( n 1 ) T n 2 ( g ( p o s ) ) = w ( n 1 ) g ( p o s + n 2 ) = T n 1 ( g ( p o s + n 2 ) ) = g ( p o s + n 2 + n 1 ) = T n 1 + n 2 ( g ( p o s ) ) = w ( n 1 + n 2 ) g ( p o s ) \begin{aligned} w(n_1)w(n_2)g(pos) &= w(n_1)T_{n_2}(g(pos)) =w(n_1)g(pos+n_2) \\ & = T_{n_1}(g(pos+n_2)) = g(pos+n_2+n_1)\\ & = T_{n_1+n_2}(g(pos)) = w(n_1+n_2)g(pos) \end{aligned} w(n1)w(n2)g(pos)=w(n1)Tn2(g(pos))=w(n1)g(pos+n2)=Tn1(g(pos+n2))=g(pos+n2+n1)=Tn1+n2(g(pos))=w(n1+n2)g(pos)
⇒ w ( n 1 ) w ( n 2 ) = w ( n 1 + n 2 ) ⇒ w ( n ) = w ( 1 ) n \Rightarrow w(n_1)w(n_2) = w(n_1+n_2) \Rightarrow w(n) = w(1)^n ⇒w(n1)w(n2)=w(n1+n2)⇒w(n)=w(1)n,不妨记 w ( 1 ) = z 1 , g ( 0 ) = z 2 w(1) = z_1, g(0) = z_2 w(1)=z1,g(0)=z2
g ( p o s ) = g ( 0 + p o s ) = g ( 0 ) w ( p o s ) = g ( 0 ) w ( 1 ) n = z 2 z 1 p o s g(pos) = g(0+pos) = g(0)w(pos) = g(0)w(1)^n = z_2z_1^{pos} g(pos)=g(0+pos)=g(0)w(pos)=g(0)w(1)n=z2z1pos
又因为 g g g有界,因此 ∣ z 1 ∣ ≤ 1 |z_1|\le 1 ∣z1∣≤1。得证。
必要性, 已知 g ( p o s ) = z 2 z 1 p o s 且 ∣ z 1 ∣ ≤ 1 g(pos) = z_2 z_1^{pos} 且 |z_1|\le 1 g(pos)=z2z1pos且∣z1∣≤1,那么不妨取 w 满 足 w ( n ) = z 1 n w满足w(n) = z_1^n w满足w(n)=z1n,则有
g ( p o s + n ) = z 2 z 1 p o s + n = z 2 z 1 p o s z 1 n = g ( p o s ) w ( n ) = T n ( g ( p o s ) ) g(pos+n) = z_2z_1^{pos+n} = z_2z_1^{pos}z_1^n = g(pos)w(n) = T_n(g(pos)) g(pos+n)=z2z1pos+n=z2z1posz1n=g(pos)w(n)=Tn(g(pos))
因此Position-free offset transformation性得证。
再有, ∣ g ( p o s ) ∣ ≤ ∣ z 2 ∣ ∣ z 1 p o s ∣ ≤ ∣ z 2 ∣ |g(pos)|\le |z_2||z_1^{pos}| \le|z_2| ∣g(pos)∣≤∣z2∣∣z1pos∣≤∣z2∣,因此有界性也得证。必要性证毕。
##########################################################################################
将 z 1 , z 2 z_1, z_2 z1,z2写成极坐标形式 z = r ( c o s θ + i s i n θ ) = r e i θ z = r(cos\theta + i sin\theta) = re^{i\theta} z=r(cosθ+isinθ)=reiθ
⇒ g ( p o s ) = r 2 r 1 p o s e i ( θ 2 + θ 1 p o s ) \Rightarrow g(pos) = r_2r_1^{pos}e^{i(\theta_2 +\theta_1pos)} ⇒g(pos)=r2r1posei(θ2+θ1pos)
但当 ∣ z 1 ∣ < 1 |z_1| < 1 ∣z1∣<1时,当 p o s pos pos很大时,词向量将收敛到零向量,即无法对任意位置都计算出合理的词向量为了避免这种情况,论文中把 ∣ z 1 ∣ |z_1| ∣z1∣取为1
所以
g ( p o s ) = r 2 e i ( θ 2 + θ 1 p o s ) g(pos) = r_2e^{i(\theta_2 +\theta_1pos)} g(pos)=r2ei(θ2+θ1pos)
重新记为
g j ( p o s ) = r j e i ( w j p o s + θ j ) g_{j}(pos) = r_je^{i(w_jpos+\theta_j)} gj(pos)=rjei(wjpos+θj)
其中 r j , w j , θ j r_j, w_j,\theta_j rj,wj,θj都是可训练参数,论文通过实验发现直接将 θ j \theta_j θj置零的效果比将其加入训练要好一点,因此我们只需要看
g j ( p o s ) = r j e i w j p o s g_{j}(pos) = r_je^{iw_jpos} gj(pos)=rjeiwjpos
可解释性
- r j r_j rj只和词在词表中的索引有关,表示词的含义,和普通的词向量对应。
- w j w_j wj表示词对位置的敏感程度。当 w j w_j wj很小时,同一个词在不同位置的词向量几乎是常量。这时的复值词向量对位置不敏感,和普通的不考虑位置信息的词向量相似。当 w j w_j wj很大时,复值词向量对位置非常敏感,会随位置变化而剧烈变化。因此 w j w_j wj可以看作是调节词向量与位置向量比重的自适应参数

图中的p= 2 π w j \frac{2\pi}{w_j} wj2π,波浪线与虚线的交点即不同pos的取值,可以看出周期p与向量对位置的敏感度相关
与Sinusoidal Position Embedding的关系
Sinusoidal Position Embedding的定义为
P E ( p o s , 2 k ) = s i n ( p o s 1000 0 2 k d m o d e l ) P E ( p o s , 2 k + 1 ) = c o s ( p o s 1000 0 2 k d m o d e l ) \begin{aligned} PE(pos,2k) & = sin(\frac{pos}{10000^{\frac{2k}{d_{model}}}})\\ PE(pos,2k+1) & = cos(\frac{pos}{10000^{\frac{2k}{d_{model}}}}) \end{aligned} PE(pos,2k)PE(pos,2k+1)=sin(10000dmodel2kpos)=cos(10000dmodel2kpos)
将 g j , k ( p o s ) = r j , k e i w j , k × p o s g_{j,k}(pos) = r_{j,k}e^{iw_{j,k}\times pos} gj,k(pos)=rj,keiwj,k×pos中的 w j , k w_{j,k} wj,k取为 1 1000 0 2 k d m o d e l \frac{1}{10000^{\frac{2k}{d_{model}}}} 10000dmodel2k1,那么
g j , k ( p o s ) = r j , k ( c o s ( p o s 1000 0 2 k d m o d e l ) + i s i n ( p o s 1000 0 2 k d m o d e l ) ) = r j , k ( P E ( p o s , 2 k + 1 ) + i P E ( p o s , 2 k ) ) \begin{aligned} g_{j,k}(pos) &= r_{j,k}(cos(\frac{pos}{10000^{\frac{2k}{d_{model}}}}) + i sin(\frac{pos}{10000^{\frac{2k}{d_{model}}}}))\\ & = r_{j,k}(PE(pos,2k+1) + iPE(pos,2k) ) \end{aligned} gj,k(pos)=rj,k(cos(10000dmodel2kpos)+isin(10000dmodel2kpos))=rj,k(PE(pos,2k+1)+iPE(pos,2k))
所以一定程度上Sinusoidal Position Embedding等级于是Complex Embeddings的一种特殊情况。
- 是否可以解释Transformer中为什么要取10000,因为这个数太大的话,那么位置编码对位置就不敏感;如果太小的化,位置编码又对位置太敏感。(需要实验测一下)
实验结果
##########################################################################################
实验1:文本分类,对比了不使用位置编码,使用可学习的位置编码(PE),使用三角函数计算得到的位置编码(TPE),不使用位置编码的复值词向量(Complex-vanilla)和本文提出的复值词向量(Complex-order)五种设置下FastText,LSTM,CNN和Transformer

结论:三角 PE 与 Train PE 几乎没什么区别。 Complex order 对模型有一定提升,但不是特别多
##########################################################################################
实验2:在WMT-16 EN-DE数据集上进行了机器翻译任务的实验

结论:使用复值词向量的Transformer相比一般的Transformer有1.3个BLEU的提升
##########################################################################################
实验3:在text8数据集上进行了语言模型实验

结论:使用复值词向量的Transformer-XL相较使用词向量加位置编码的Transformer-XL有明显提升
位置特征与内容特征间的关系
Paper: Constituency Parsing with a Self-Attentive Encoder
尽管这篇文章主要是提出了一种新型的句法分析模型。但其中关于位置编码的实验比较有趣,这里也记录一下。
我们都知道Transformer模型里的self-attentive结构如下:
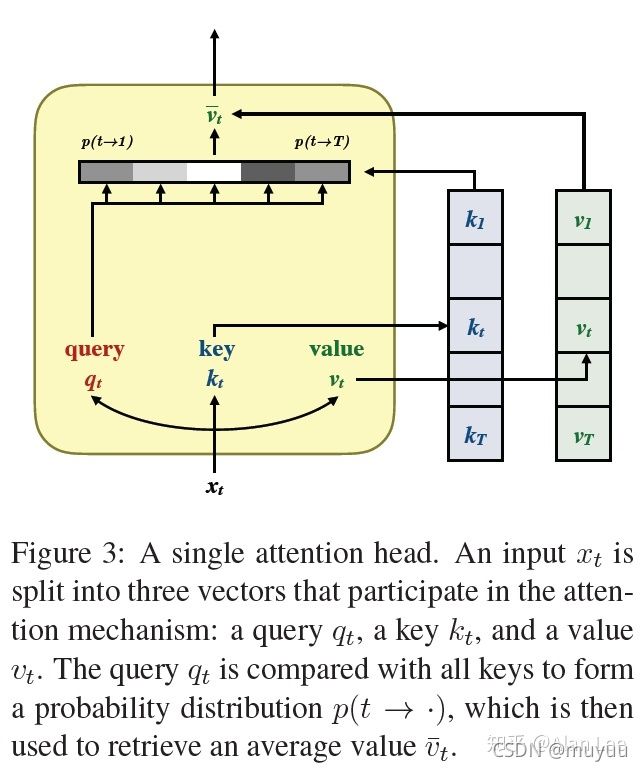
其中 x t = w t + p t x_t = w_t + p_t xt=wt+pt, w t w_t wt是内容特征, p t p_t pt是位置特征。然后利用 x t x_t xt分别计算 Q t , K t , V t Q_t,K_t,V_t Qt,Kt,Vt:
Q t = W q x t , K t = W k x t , V t = W v x t Q_t = W_q x_t,K_t = W_k x_t,V_t = W_v x_t Qt=Wqxt,Kt=Wkxt,Vt=Wvxt
最后根据attention公式:
S i n g l e H e a d ( X ) = SoftMax ( Q K T d k ) V SingleHead(X) = \text {SoftMax}(\frac{QK^T}{\sqrt d_k})V SingleHead(X)=SoftMax(dkQKT)V
来获取带自注意力的特征。
去掉内容特征
为了了解位置特征和内容特征的relative importance,文章做了一个实验,在计算 Q t Q_t Qt和 K t K_t Kt的时候,只保留了位置特征,而去掉了内容特征,而计算 V t V_t Vt仍保留了内容特征,即:
Q t = W q p t , K t = W k p t , V t = W v ( w t + p t ) Q_t = W_q p_t,K_t = W_k p_t,V_t = W_v (w_t+p_t) Qt=Wqpt,Kt=Wkpt,Vt=Wv(wt+pt)
解释:相当于在计算每个词的attentive weight时,只考虑位置信息,而不考虑词语本身的信息。由于本文的任务是做句法分析,因此是在测试只考虑位置信息的attentive weight会对结果有多大的影响。
结果:F1 score只降了0.27
结论:由于多头结构的存在,即使attentive weight只考虑了位置信息,这个结构也相当于一个多层的cnn,而且value矩阵 V t V_t Vt仍保留了内容特征,因此结果应该依然不错。但是只有这么小的drop依然出乎作者意料之外。
##########################################################################################
将embedding相加改为拼接
接下来,作者猜想直接将两种特征相加,可能会让其中一种信息占主导作用,模型不能很好的找到两种特征重要性的平衡。
事实上,观察注意力权重 SoftMax ( Q K T d k ) \text {SoftMax}(\frac{QK^T}{\sqrt d_k}) SoftMax(dkQKT),不难发现:
q ⋅ k = ( q w + q p ) ⋅ ( k w + k p ) = q w k w + q w k p + q p k w + q p k p q\cdot k = (q^w + q^p) \cdot (k^w + k^p) = q^w k^w + q^w k^p + q^p k^w + q^p k^p q⋅k=(qw+qp)⋅(kw+kp)=qwkw+qwkp+qpkw+qpkp
其中的交叉项 q w k p + q p k w q^w k^p + q^p k^w qwkp+qpkw 可能存在隐患,例如这可能会导致得到这样一个网络:单词 the 总是会特别注意句子的第 5 个位置。这种交叉注意力似乎并没有太大作用,反而会带来过拟合。
因此这个实验里,作者尝试将两种特征由相加改成拼接的方式: x t = [ w t ; p t ] x_t = [w_t; p_t] xt=[wt;pt],其他不变。
结果:比相加的方式还降了0.07个F1 score
结论:事实上,adding 和 concatenation 在高维度上的表现是差不多的,尤其是当结果会立马乘上一个矩阵之后,因为这样会混合里面的信息。
##########################################################################################
拆分位置特征和内容特征
拼接方法效果不行,文章中又尝试了一种新的分解方式,对于 x t = [ w t ; p t ] x_t = [w_t; p_t] xt=[wt;pt],将参数矩阵 W W W也进行拆分:
Q t = W q w w t + W q p p t , K t = W k w w t + W k p p t , V t = W v w w t + W v p p t Q_t = W_q^w w_t + W_q^p p_t,K_t = W_k^w w_t + W_k^p p_t,V_t = W_v^w w_t + W_v^p p_t Qt=Wqwwt+Wqppt,Kt=Wkwwt+Wkppt,Vt=Wvwwt+Wvppt
包括后面的 Q ⋅ K Q\cdot K Q⋅K也变成:
Q t ⋅ K t = Q t w ⋅ K t w + Q t p ⋅ K t p = W q w w t ⋅ W k w w t + W q p p t ⋅ W k p p t Q_t \cdot K_t = Q_t^w \cdot K_t^w + Q_t^p \cdot K_t^p = W_q^w w_t \cdot W_k^w w_t + W_q^p p_t \cdot W_k^p p_t Qt⋅Kt=Qtw⋅Ktw+Qtp⋅Ktp=Wqwwt⋅Wkwwt+Wqppt⋅Wkppt
对于一个 attention head 来说,拆分后的情况如图所示,可以看成分别对 w t w_t wt 和 p t p_t pt 应用注意力,后续的 feed-forward 层也同样拆分。

结果:F1 score提升了约0.5
结论:表明拆分不同类型的特征确实能得到一个不错的结果。
##########################################################################################
在测试时分别disable位置特征和内容特征
为了分析模型对内容和位置注意力的利用情况,作者又做了个实验,模型训练保持不变,但是在测试阶段,把内容注意力或位置注意力人为置零,即禁用。

结论:位置注意力相当重要,但是内容注意力也有一定帮助,尤其是在最后几层
Reference:
- 【工大SCIR笔记】浅谈Transformer模型中的位置表示
- Encoding word order in complex embeddings (2020)
- Constituency Parsing with a Self-Attensive Encoder