编程作业（python）| 吴恩达机器学习（3）多分类与神经网络

8道编程作业及解析见：Coursera吴恩达机器学习编程作业
编程环境：Jupyter Notebook

Programming Exercise 3：Multi-class Classification and Neural Network

题目：手写数字识别

原始数据集的标签 $y$ 取值为1到10，$y=10$表示当前手写字为0，其余1到9即对应1到9。

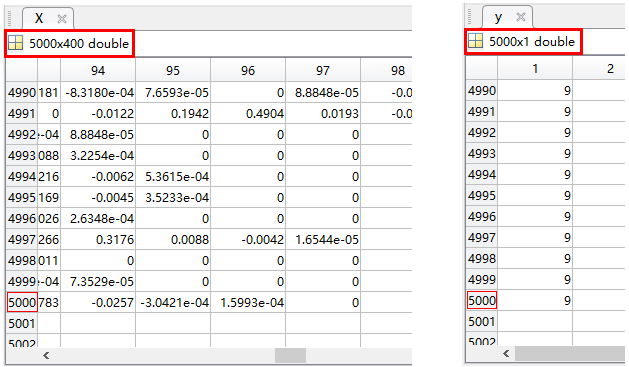
数据集保存在 ex3data1.mat，注意文件格式跟之前不一样，用matlab打开可以看到有$X$和$y$两个变量：

• $X$的维度是5000×400，表示有5000个样本，每个样本有400个特征（其实就是20×20的像素值）
• $y$的维度是5000×1，表示有5000个样本，每个样本对应1个标签（1到10共十种标签值，每种标签有500个样本）

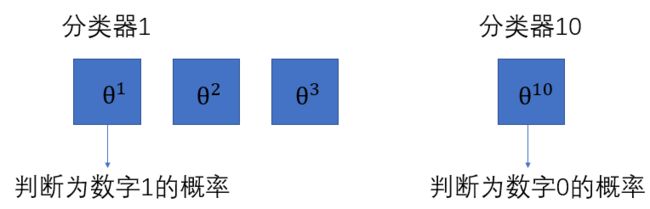
显然，这是个多分类问题（十分类问题），可以用多分类逻辑回归或者神经网络解决。

1. 多分类逻辑回归

关于多分类逻辑回归的原理参阅 6.多类别分类问题 one vs all

1.1 导入数据

本次作业中的数据集是.mat格式，需要用到scipy库导入

• 导入库与数据集：

  import numpy as np  			# 科学计算库，处理多维数组，进行数据分析
  import matplotlib.pyplot as plt # 提供一个类似 Matlab 的绘图框架
  import scipy.io as sio 			# 数据输入输出，用于读入.mat文件。scipy一个高级的科学计算库，它和Numpy联系很密切
  
  data = sio.loadmat('ex3data1.mat')
  

• 查看数据类型：
  

• 手写数字图像可视化：由于导入的data是字典类型，因此用键值来获取$X$并打印出图像

  raw_X = data['X']	# raw_X 维度是(5000,400)
  raw_y = data['y']	# raw_y 维度是(5000,1)
  
  def plot_100_image(X):
  	sample_index = np.random.choice(len(X),100)#从样本集中随机选取100个打印
      images = X[sample_index,:]#选取该行，所有列（即对应一个样本）   	
  	print(images.shape)
  	# 创建绘图实例
  	fig,ax = plt.subplots(ncols=10,nrows=10,figsize=(5,5),  #10×10共100张图，总窗口大小为5×5
  						  sharex=True,sharey=True)			#所有图像共享x,y轴属性
  	plt.xticks([]) #隐藏x,y轴坐标刻度
  	plt.yticks([])
  	
  	for r in range(10):#行
      	for c in range(10):#列
          	ax[r,c].imshow(images[10 * r + c].reshape(20,20).T,cmap='gray_r')
          
  	plt.show
  

1.2 使用scipy优化函数

之前的两次作业中，在定义代价函数和梯度下降函数后，我们都是 手动 定义学习率alpha和梯度下降的迭代次数iters来得到最终优化的参数集 $\theta$。

本练习中我们利用scipy库中的一个优化函数来 自动优化 模型参数，该函数可以根据输入的参数 返回最终优化的参数集，其定义如下如下：

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
（附上该函数官方文档）

输入参数有一大堆，本练习中我们只用到以下几个：

• fun： 要优化的函数，即代价函数costFunction
• x0：初始的参数值，即 $\theta$
• args=()：其他参数，例如$X$，$y$ 以及正则化项系数 $\lambda$ 等
• method：求极值的方法，官方文档给了很多种，我们选择TNC算法（截断牛顿法）
• jac：梯度下降算法中的梯度向量

下面我们就定义要用到的参数：

1.2.1 构造数据集

X = np.insert(raw_X,$x_0$,values=1,axis=1) # 在首列插入x0=1的一列。axis=1表示按列插入
y = raw_y.flatten()# 使得到的 y为一维数组

可以用 X.shape 和y.shape 查看数组的维度 ，维度分别为(5000,401)和(5000,)

1.2.2 定义代价函数

# 逻辑函数
def sigmoid(z):    
	return 1 / (1 + np.exp(-z))

# 代价函数
def costFunction(X,y,theta,lamda):
	A = sigmoid( X @ theta)# 假设函数
	
	first = y * np.log(A)
	second = (1-y) * np.log(1-A)
	reg = np.sum(np.power(theta[1:],2)) * (lamda / (2 * len(X)))#注意正则化项的θ是从j=1开始
	
	return -np.sum(first + second) / len(X) + reg

1.2.3 定义梯度向量（带正则项）

建议与 2.5梯度下降函数 对照看一下
$$\theta =\theta -\alpha \frac{1}{m}{X}^T\left[g(X\theta )-y\right]-\alpha \frac{\lambda }{m}{\theta }^{reg}，其中{\theta }_0^{reg}=0，其余项与\theta 相等$$

def gradient_reg(theta,X,y,lamda):
    reg = theta[1:] * (lamda / len(X))
    reg = np.insert(reg,0,values=0,axis=0)
    
    first = (X.T@(sigmoid(X@theta) - y)) / len(X)
    
    return first + reg # 注意返回的是一个向量，维度与 theta一致

1.2.4 定义优化函数

from scipy.optimize import minimize

def one_vs_all(X,y,lamda,K):# K为标签个数
    
    n = X.shape[1] # 特征数量，本例中为 401
    
    # 总的参数向量维度是K×n(本例中为10×401)，相当于构建了K个分类器，每个分类器最后都会得到一个优化参数集
    theta_all = np.zeros((K,n)) 
    
    for i in range(1,K+1):
        theta_i = np.zeros(n,)# 第 i个分类器的参数集
        
        result = minimize(fun =costFunction,
                      x0 = theta_i,
                      args = (X, y == i,lamda),# y==i表示当前分类器需要判别 y属于哪个标签值
                      method = 'TNC',
                      jac = gradient_reg )
        theta_all[i-1,:] = result.x # 表示当前分类器的最优 θ
        
    return theta_all # 将K个分类器的优化结果保存在theta_all

1.3 计算分类准确率

给正则化系数lamda和分类器个数K赋上初值，来查看下最终的优化参数：

lamda = 1
K = 10
theta_final = one_vs_all(X,y,lamda,K)

可以得到theta_final的结果是10个分类器的最优化参数

由于本例的样本是图像，无法像上一章那样通过绘图就可以大概看出分类的准确率，只能靠计算得出：

def predict(X,theta_final):
    # 5000个样本，每个样本都有10个预测输出（概率值）
    pro = sigmoid(X@theta_final.T) #(5000,401) (10,401)^T=>(5000,10) 
    
    # 每个样本取自己10个预测中最大的值作为最终预测值
    h_argmax = np.argmax(h,axis=1)# 按列比较，argmax表示返回该行最大值对应的列索引
    
    return h_argmax + 1 # 返回列索引为0表示标签值为1，返回列索引为9表示标签值为10（代表数字0）
    
y_pre = predict(X,theta_final)
acc = np.mean(y_pre == y)

得到准确率为acc = 0.9446

2. 神经网络-前向传播

神经网络前向传播过程原理参阅 神经网络模型构建

案例： 手写数字识别
数据集：ex3data1.mat
参数集：ex3weights.mat

题目和数据集不变，但直接给出了神经网络的训练参数结果，所以本练习只是简单用代码了解神经网络的前向传播过程，不涉及训练过程。

2.1 获取数据集

import numpy as np
import scipy.io as sio

data = sio.loadmat('ex3data1.mat')
raw_X = data['X'] # (5000,400)
raw_y = data['y'] # (5000,1)
`
X = np.insert(raw_X,0,values=1,axis=1) # (5000, 401)
y = raw_y.flatten()					   # (5000,)

2.2 获取训练参数

theta = sio.loadmat('ex3weights.mat')
>>> theta.keys()
dict_keys(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])

theta1 = theta['Theta1'] # (25, 401)
theta2 = theta['Theta2'] # (10, 26)

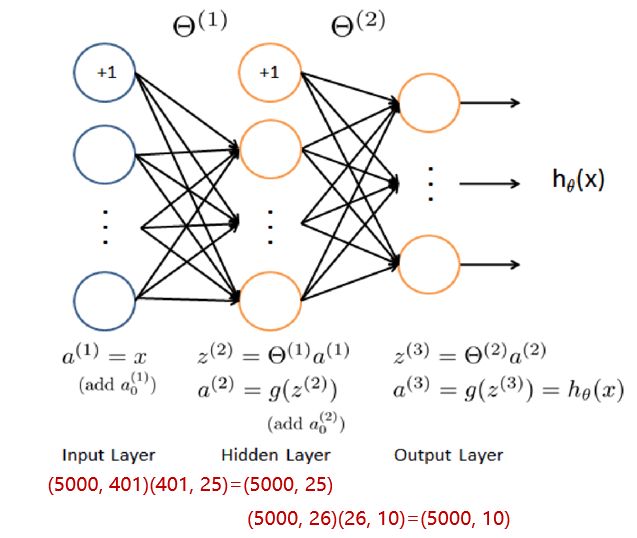
2.3 前向传播过程

作业中给出的隐含层为 26 个单元，并且已经给出了层与层之前的权值矩阵

# 定义激活函数
def sigmoid(z):
return 1/ (1 + np.exp(-z))
	
# 输入层
a1 = X # a1.shape=(5000, 401)

# 隐藏层
z2 = X @theta1.T # (5000, 401)(401, 25) = (5000, 25)
a2 = sigmoid(z2) # a2.shape=(5000, 25)

# 输出层
a2 = np.insert(a2,0,values=1,axis=1) # (5000, 26)
z3 = a2 @ theta2.T 					 # (5000, 26)(26, 10) = (5000, 10)
a3 = sigmoid(z3) 					 # a3.shape=(5000, 10)

2.4 计算分类准确率

上一步得到的a3维度是(5000, 10)，即5000个样本，每个样本都输出10个预测输出（概率值）

# 同1.3节
y_pre = np.argmax(a3,axis=1)
y_pre = y_pre + 1

# 计算分类准确率
acc =  np.mean(y_pred == y)

得到准确率为acc = 0.9752