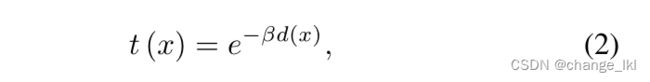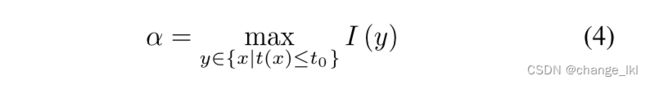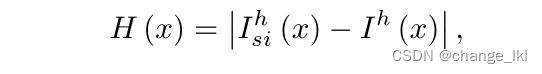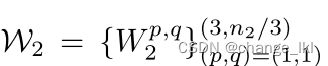DehazeNet: An End-to-End System for Single ImageHaze Removal（图像去雾2016）
摘要：
在这篇文章中，提出了一个可训练的端到端系统称为DehazeNet，用于介质传输估计。DehazeNet将一幅有雾的图像作为输入，输出其介质透射图，然后通过大气散射模型恢复出一幅无雾的图像。DehazeNet采用基于卷积神经网络(CNN)的深度架构，其层是专门设计来体现图像去雾中的既定假设/先验。具体来说，Maxout单元层用于特征提取，可以生成几乎所有的与雾向光的特征。我们还在去雾网中提出了一种新的非线性激活函数，称为双边校正线性单元(BReLU ),它能够提高恢复的无雾图像的质量。在提出的去雾网的组件和现有方法中使用的组件之间建立联系。
本文贡献：
（1）DehazeNet是一个端到端的系统。它直接学习和估计模糊图像块与其介质传输之间的映射关系。这是通过其深层架构的特殊设计来实现的，以体现既定的图像去雾原则。
（2）我们在DehazeNet中提出了一种新的非线性激活函数，称为双边校正线性单元1(BReLU)。BReLU扩展了校正线性单元(ReLU ),并证明了它在获得精确图像恢复中的重要性。在技术上，BReLU使用双边约束来减少搜索空间和提高收敛性。
（3）我们建立了去雾网的组件与现有去雾方法中使用的那些假设/先验之间的联系，并解释了去雾网通过端到端自动学习所有这些组件来改进这些方法
related work
大气散射模型
I(x)是观测到的朦胧图像，J(x)是要复原的真实场景，t(x)是介质透射，α是全球大气光
d(x)是场景点到摄像机的距离，β是大气的散射系数
d(x)趋于无穷大时，t(x)趋近于零
全局大气光的估计
相关工作
暗通道:
暗通道先验是基于对室外无霾图像的广泛观察。在大多数无霾色块中，至少一个颜色通道具有一些亮度值非常低甚至接近于零的像素。暗通道[9]定义为局部区域中所有像素颜色的最小值:
最大对比度
颜色衰减
当场景的颜色在薄雾的影响下褪色时，片的饱和度
(x)急剧下降，并且亮度值
(x)增加，同时产生高的差值。根据上面的颜色衰减先验，利用亮度和饱和度之间的差异来估计雾霾的浓度
在HSV颜色空间中
(x)=
颜色衰减特征与场景深度d(x)∝A(x)成比例
色调差异
原始图像I(x)和它的半逆图像之间的色调差异
(x) = max [
(x),1-(x)]with c ∈{ r，g，b}已经用于检测雾度。对于无霾图像，其半逆图像的三个通道中的像素值不会全部翻转，从而导致(x)和I(x)之间的色调变化较大。色调差异特征被定义为
上标“h”表示HSV颜色空间中图像的色调通道
DehazeNet的提出
DehazeNet，这是一个可训练的端到端系统，它可以明确地学习原始模糊图像与其相关联的介质传输图之间的映射关系。
去雾网的层设计
DehazeNet由级联的卷积层和池化层组成，其中一些层之后采用了适当的非线性激活函数。图2展示了去雾网络的架构。DehazeNet的层和非线性激活的设计用于实现介质传输估计的四个顺序操作，即特征提取、多尺度映射、局部极值和非线性回归。
1)特征提取:为了解决图像去雾问题的不适定性，现有方法提出了各种假设，并且基于这些假设，它们能够在图像域上密集地提取雾度相关特征(例如，暗通道、色调差异和颜色衰减)。注意，密集地提取这些模糊相关特征等同于用适当的滤波器卷积输入模糊图像，然后进行非线性映射。受这些雾度相关特征的颜色通道中的极值处理的启发，一种称为Maxout单元的不寻常的激活函数被选择作为降维的非线性映射。Maxout单元是在多层感知机或CNN中使用的简单前馈非线性激活函数。当在CNN中使用时，它通过对k个相关特征图进行逐像素最大化操作来生成新的特征图。基于最大输出单元，我们设计第一层去雾网络如下
代表过滤器
代表偏差
*代表卷积操作，在第一层中有n1个输出特征图
是kXn1个卷积滤波器之一，3是输入图像的通道数，f1滤波器的空间尺寸，最大输出单元将kn1维向量中的每一个映射成一个n1维向量，并通过自动学习而不是现有方法中的启发式方法来提取雾霾相关特征
多尺度映射
去雾网络的第二层中使用并行卷积运算，其中任何卷积滤波器的大小在3×3、5×5和7×7之间，并且我们对这三个尺度使用相同数量的滤波器。
n2是第二层的输出维度，
局部极值
每个像素下考虑邻域最大值以克服局部敏感性。此外，局部极值符合介质传输是局部恒定的假设，并且通常是为了克服传输估计的噪声。在DehazeNet的第三层使用局部极值运算。
第三层的输出维数那n3= n2。与CNN中通常降低特征图分辨率的最大池化相反，这里的局部极值运算是密集应用于每个特征图像素能够保持分辨率以用于图像恢复。
非线性回归
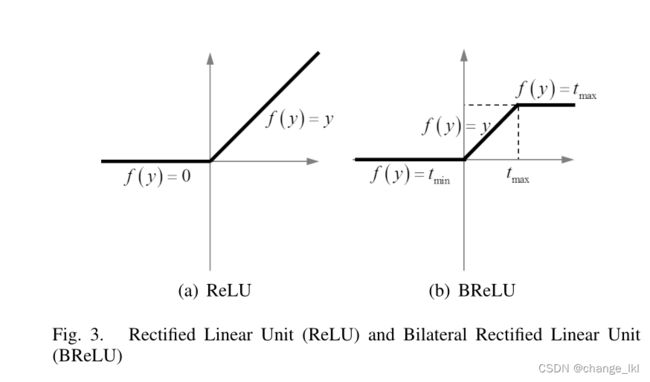
深度网络中非线性激活函数的标准选择包括Sigmoid 和整流线性单元(ReLU)。前一种方法易受梯度消失的影响，导致网络训练收敛速度慢或局部最优。为了克服消失梯度的问题，提出了ReLU[,它提供了稀疏表示。然而，ReLU是为分类问题设计的，并不完全适合于回归问题，如图像恢复。特别是，ReLU仅在值小于零时禁止值。这可能导致响应溢出，特别是在最后一层，因为对于图像恢复，最后一层的输出值应该在一个小范围内既是上界又是下界。为此，我们提出了双边整流线性单元(BReLU)激活函数，如图3所示，以克服这一限制。受Sigmoid和ReLU的启发，BReLU作为一种新的线性单元保持了双边约束和局部线性。基于所提出的BReLU，第四层的特征图被定义为
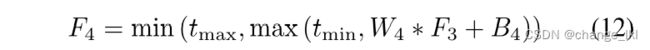W4 = { W4 }包含一个大小为3×f4×f4的滤波器，B4 = { B4 }包含一个偏差，而tmin，max是BReLU的临界值(本文中tmin =0，max = 1)。可以示出该激活函数的梯度
上述四层级联在一起以形成基于CNN的可训练端到端系统，其中与卷积层相关联的滤波器和偏差是要学习的网络参数。
与传统去雾方法的联系
DehazeNet中的第F1是为与雾相关特征提取而设计的。暗通道特征为例，如果权重w1是相反的过滤器(在一个通道的中心具有值-1的稀疏矩阵，如图4(a))并且B1是单位偏差，则特征图的最大输出相当于颜色通道的最小值，这类似于暗通道[9](参见等式(5))。同样，当权重是如图4(c)的圆形滤波器时，f1类似于最大对比度[7](见等式(6))；当w1包括全通滤波器和反向滤波器时，f1类似于最大和最小特征图，是从RGB到HSV的颜色空间变换的原子操作，然后提取颜色衰减[18](见等式(7))和色调视差(见等式(8))特征。总之，在图4(e)所示的滤波器学习成功后，在第二节中提到的雾度相关特征。II-B可以潜在地从第一层DehazeNet中提取。另一方面，最大输出激活函数可以被认为是对任意凸函数的分段线性逼近。在本文中，我们选择四个特征图(k= 4)中的最大值来逼近任意凸函数，如图4(d)所示。
图像中的白色对象类似于通常具有高亮度值和低饱和度值的重度薄雾场景。因此，几乎所有的雾度估计模型都倾向于认为白色的场景物体是远处的，导致对介质透射的不准确估计。基于场景深度局部恒定的假设，局部极值滤波是克服这一问题的常用方法[。在去雾网中，第三层操作的局部最大值滤波器消除了局部估计误差。因此，当透射率t(x)接近零时，直接衰减项J(x)t(x)可以非常接近零。直接恢复的场景rJ(x)容易受到噪声的影响。在DehazeNet中，我们提出了BReLU来限制tmin和tmax之间的传输值，从而缓解了噪声问题。