神经网络：关于模型拟合相关基础学习

1、相关概念

1.1 模型的容量

  模型的容量或表达能力，是指模型拟合复杂函数的能力。模型容量的指标为模型的假设空间(Hypothesis Space)大小，即模型可以表示的函数集的大小。假设空间越大越完备，从假设空间中搜索出逼近真实模型的函数也就越有可能；反之，如果假设空间非常受限，就很难从中找到逼近真实模型的函数。
  过大的假设空间会增加搜索难度和计算代价，在有限的计算资源的约束下，挑选合适容量的学习模型是一个很大的难题。

.

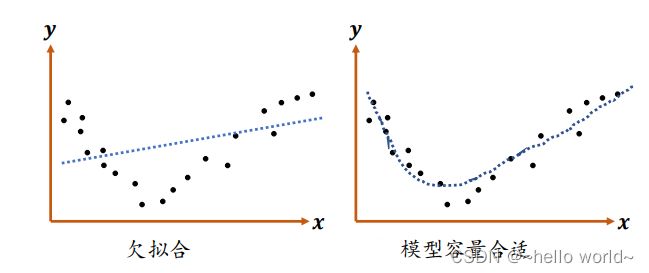
1.2 过拟合

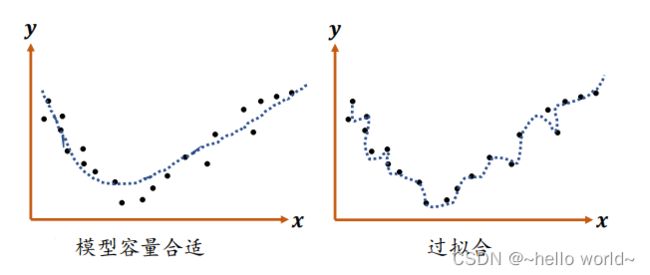
  当模型的容量过大时，网络模型除了学习到训练集数据的模态之外，还把额外的观测误差也学习进来，导致学习的模型在训练集上面表现较好，但是在未见的样本上表现不佳，也就是模型泛化能力偏弱，这种现象叫作过拟合(Overfitting)。

.

1.3 欠拟合

  当模型的容量过小时，模型不能够很好地学习到训练集数据的模态，导致训练集上表现不佳，同时在未见的样本上表现也不佳，这种现象叫作欠拟合(Underfitting)。

.

2、正则化

  通过设计不同层数、大小的网络模型可以为优化算法提供初始的函数假设空间，但是模型的实际容量可以随着网络参数的优化更新而产生变化。以多项式函数模型为例：

上述模型的容量可以通过 简单衡量。在训练的过程中，如果网络参数 ₊₁, ⋯ , 均为 0，那么网络的实际容量退化到次多项式的函数容量。因此，通过限制网络参数的稀疏性，可以来约束网络的实际容量。
  这种约束一般通过在损失函数上添加额外的参数稀疏性惩罚项实现，在未加约束之前的优化目标是:

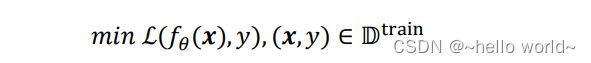
对模型的参数添加额外的约束后，优化的目标变为:

其中()表示对网络参数的稀疏性约束函数。一般地，参数 的稀疏性约束通过约束参数 的 范数实现，即

.

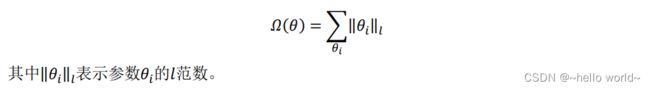
2.1 正则化的效果

  实际训练时，一般优先尝试较小的正则化系数 ，观测网络是否出现过拟合现象。然后尝试逐渐增大参数来增加网络参数稀疏性，提高泛化能力。但是，过大的参数有可能导致网络不收敛，需要根据实际任务调节。

2.2 常用的正则化：L0

  L0 正则化是指采用 L0 范数作为稀疏性惩罚项()的正则化计算方式，即

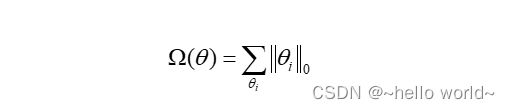
其中 L0 范数 ‖‖₀ 定义为 中非零元素的个数。通过约束 ∑‖‖₀ 的大小可以迫使网络中的连接权值大部分为 0，从而降低网络的实际参数量和网络容量。但是由于 L0 范数 ‖‖₀ 并不可导，不能利用梯度下降算法进行优化，在神经网络中使用的并不多。
.

2.3 常用的正则化：L1

   采用 L1 范数作为稀疏性惩罚项 () 的正则化计算方式叫作 L1 正则化，即

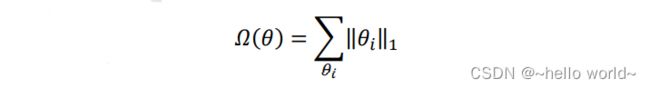
其中 L1 范数 ‖‖₁ 定义为张量 中所有元素的绝对值之和。L1 正则化也叫 Lasso Regularization，它是连续可导的，在神经网络中使用广泛。

   L1 正则化实现如下:

import tensorflow as tf
# 创建网络参数 w1,w2
w1 = tf.random.normal([4,3])
w2 = tf.random.normal([4,2])

# 计算 L1 正则化项,所有元素的绝对值之和
loss_reg = tf.reduce_sum(tf.math.abs(w1)) + tf.reduce_sum(tf.math.abs(w2))

.

2.4 常用的正则化：L2

   采用 L2 范数作为稀疏性惩罚项 () 的正则化计算方式叫做 L2 正则化，即

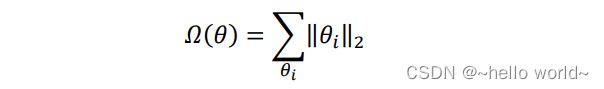
其中 L2 范数 ‖‖₂ 定义为张量 中所有元素的平方和。L2 正则化也叫 Ridge Regularization，与 L1 正则化一样，是连续可导的，在神经网络中使用广泛。
   L2 正则化实现如下:

# 创建网络参数 w1,w2
w1 = tf.random.normal([4,3])
w2 = tf.random.normal([4,2])

# 计算 L2 正则化项，所有元素的平方和
loss_reg = tf.reduce_sum(tf.square(w1)) + tf.reduce_sum(tf.square(w2))

.

3、Dropout

   Dropout 方法主要用来提高模型性能。Dropout 通过随机断开神经网络的连接，减少每次训练时实际参与计算的模型的参数量；但是在测试时，Dropout 会恢复所有的连接，保证模型测试时获得最好的性能。

虚线代表了采样结果为断开的连接线，实线代表了采样结果不断开的连接线。
   在 TensorFlow 中，可以通过 tf.nn.dropout(x, rate)函数实现某条连接的 Dropout 功能，其中 rate 参数设置断开的概率值。例如：

# 添加 dropout 操作，断开概率为 0.5
x = tf.nn.dropout(x, rate=0.5)

也可以将 Dropout 作为一个网络层使用，在网络中间插入一个 Dropout 层。例如：

# 添加 Dropout 层，断开概率为 0.5
model.add(layers.Dropout(rate=0.5))

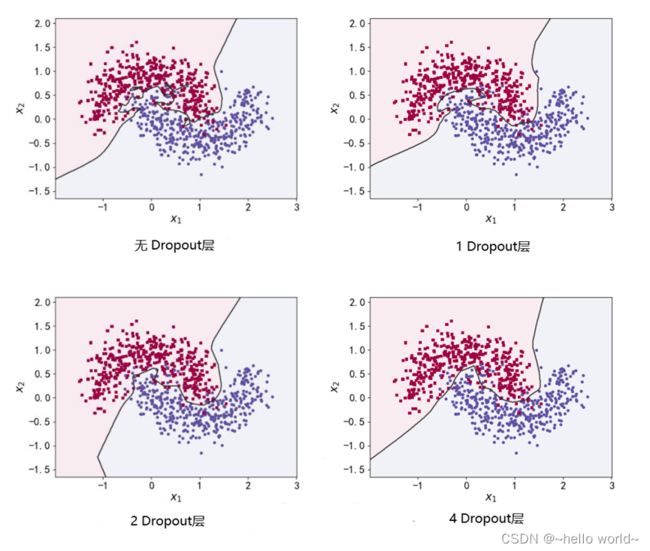
   为了验证 Dropout 层对网络训练的影响，在维持网络层数等超参数不变的条件下，通过在 5 层的全连接层中间隔插入不同数量的 Dropout 层来观测 Dropout 对网络训练的影响。可以看到，在不添加 Dropout 层时，网络模型与之前观测的结果一样，出现了明显的过拟合现象；随着 Dropout 层的增加，网络模型训练时的实际容减少，泛化能力变强。

.

4、过拟合问题实战

  基于月牙形状的 2 分类数据集的过拟合与欠拟合模型，进
行完整的实战。

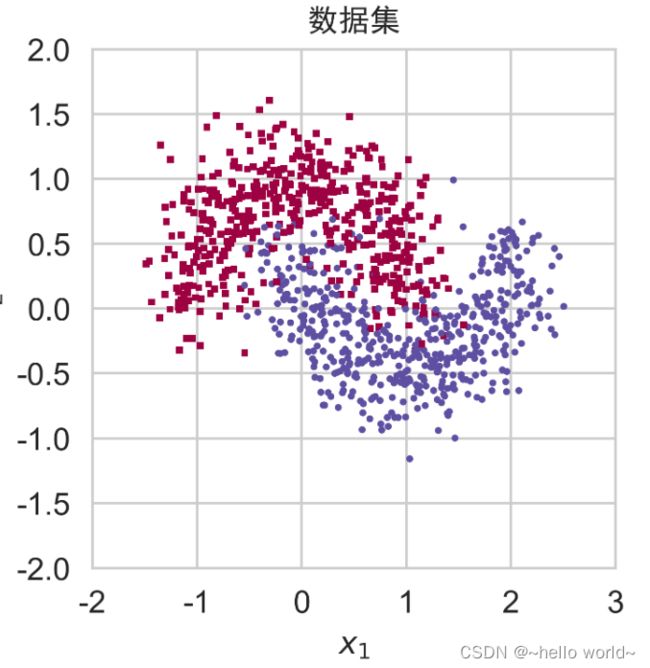
4.1 构建数据集

import numpy as np 
import seaborn as sns
import tensorflow as tf 
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams["axes.unicode_minus"] = False

# 为了演示过拟合现象，我们只采样了 1000 个样本数据，同时添加标准差为 0.25 的高斯噪声数据
# 从 moon 分布中随机采样 1000 个点，并切分为训练集-测试集

N_SAMPLES = 1000 # 采样点数
TEST_SIZE = None # 测试数量比率
X, y = make_moons(n_samples = N_SAMPLES, noise=0.25, random_state=100)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = TEST_SIZE, random_state=50)


def make_plot(X, y, plot_name,XX=None, YY=None, preds=None, dark=False):    
    if dark:
        plt.style.use('dark_background')
    else:
        sns.set_style("whitegrid")
    # 分辨率参数-dpi，画布大小参数-figsize
    plt.figure(dpi=200,figsize=(10,10))   
    axes = plt.gca()
    axes.set_xlim([-2,3])
    axes.set_ylim([-2,2])
    axes.set(xlabel="$x_1$", ylabel="$x_2$")
    plt.title(plot_name, fontsize=10,fontproperties='SimHei')
    # 根据网络输出绘制预测曲面
    if(XX is not None and YY is not None and preds is not None):
        plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha = 0.08)
        plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5],cmap="Greys", vmin=0, vmax=0.6)
    
    # 绘制正负样本
    markers = ['o' if i == 1 else 's' for i in y.ravel()]
    mscatter(X[:, 0], X[:, 1], c=y.ravel(), s=10, cmap=plt.cm.Spectral, edgecolors='none', m=markers, ax=axes)

def mscatter(x, y, ax=None, m=None, **kw):
    import matplotlib.markers as mmarkers
    if not ax: ax = plt.gca()
    sc = ax.scatter(x, y, **kw)
    if (m is not None) and (len(m) == len(x)):
        paths = []
        for marker in m:
            if isinstance(marker, mmarkers.MarkerStyle):
                marker_obj = marker
            else:
                marker_obj = mmarkers.MarkerStyle(marker)
            path = marker_obj.get_path().transformed(
                marker_obj.get_transform())
            paths.append(path)
        sc.set_paths(paths)
    return sc

make_plot(X, y, "数据集")

.

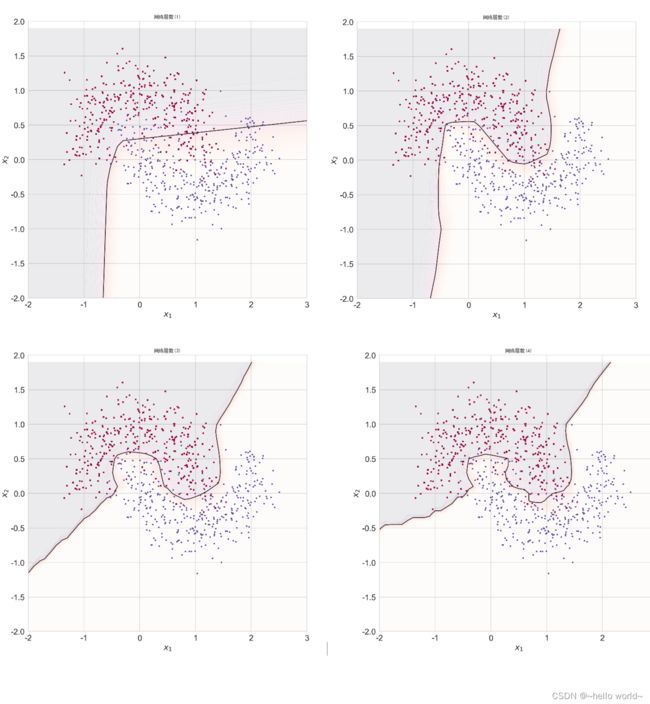
4.2 网络层数的影响

  为了探讨不同的网络深度下的过拟合程度，我们共进行了 5 次训练实验。在 ∈ [0,4] 时，构建网络层数为 +2 层的全连接层网络，并通过 Adam 优化器训练 500 个 Epoch，获得网络在训练集上的分隔曲线，如图。

def network_layers_influence(x_train, y_train):
    for n in range(5): # 构建 5 种不同层数的网络
        model = Sequential()# 创建容器
        
        # 创建第一层
        model.add(Dense(8, input_dim=2,activation='relu'))
        
        for _ in range(n): # 添加 n 层，共 n+2 层
            model.add(Dense(32, activation='relu'))
            
        model.add(Dense(1, activation='sigmoid')) # 创建最末层
        model.compile(loss='binary_crossentropy', optimizer='adam',metrics=['accuracy']) # 模型装配与训练
        history = model.fit(X_train, y_train, epochs=500, verbose=1)
    
        # 绘制不同层数的网络决策边界曲线       
        xx = np.arange(-2, 10, 0.1)       
        yy = np.arange(-2, 2, 0.1)
        
        # 生成 x-y 平面采样网格点，方便可视化
        XX, YY = np.meshgrid(xx, yy)
        preds = model.predict(np.c_[XX.ravel(), YY.ravel()])    
      
        title = "网络层数({})".format(n)        

        make_plot(X_train, y_train, title,XX, YY, preds)
      
        
network_layers_influence(X_train, y_train)

.

4.3 Dropout 的影响

  为了探讨 Dropout 层对网络训练的影响，我们共进行了 5 次实验，每次实验使用 7 层的全连接层网络进行训练，但是在全连接层中间隔插入 0~4 个 Dropout 层，并通过 Adam 优化器训练 500 个 Epoch，网络训练效果如图所示。

def dropout_influence(x_train, y_train):
    for n in range(5):
        model = Sequential()
        model.add(Dense(8, input_dim=2, activation='relu'))
        count = 0
        for _ in range(5):
            model.add(Dense(64, activation='relu'))
            if count < n:
                count += 1
                model.add(layers.Dropout(rate=0.5))
        model.add(Dense(1, activation='sigmoid'))
        model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
        history = model.fit(X_train, y_train, epochs=500, verbose=1)
        # 绘制不同 Dropout 层数的决策边界曲线        
        xx = np.arange(-2, 3, 0.01)        
        yy = np.arange(-1.5, 2, 0.01)
        
        # 生成 x-y 平面采样网格点，方便可视化
        XX, YY = np.meshgrid(xx, yy)
        preds = model.predict(np.c_[XX.ravel(), YY.ravel()])
        title = "无Dropout层" if n == 0 else "{0}层 Dropout层".format(n)
        file = "Dropout_%i.png" % n
        make_plot(x_train, y_train, title, XX, YY, preds)

dropout_influence(X_train, y_train)

.

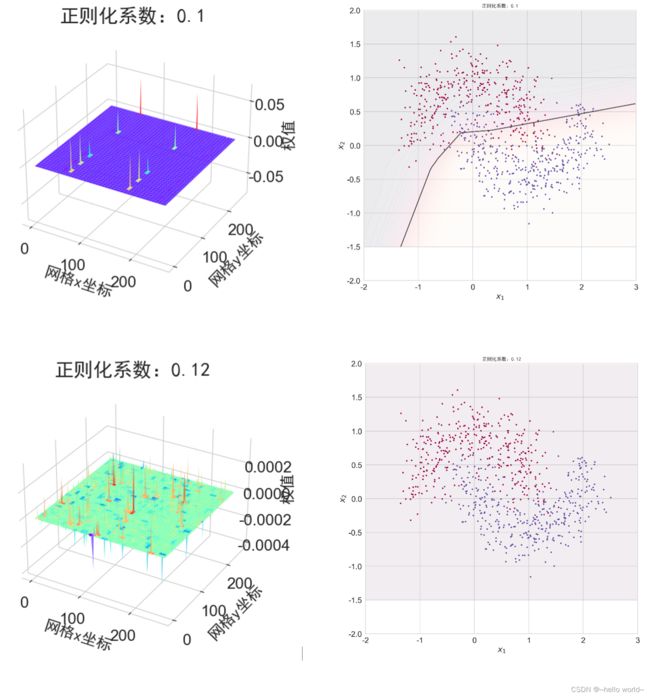
4.4 正则化的影响

为了探讨正则化系数对网络模型训练的影响，我们采用 L2 正则化方式，构建了 5 层的神经网络，其中第 2、3、4 层神经网络层的权值张量 W 均添加 L2 正则化约束项，代码如下：

def build_model_with_regularization(_lambda):
    # 创建带正则化项的神经网络
    model = Sequential()
    model.add(layers.Dense(8, input_dim=2, activation='relu'))  # 不带正则化项
    
    # 2-4层均是带 L2 正则化项
    model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda)))
    model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda)))
    model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda)))
    
    # 输出层
    model.add(layers.Dense(1, activation='sigmoid'))
    model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])  # 模型装配
    return model


def plot_weights_matrix(model, layer_index, plot_title):
    
    # 绘制权值范围函数
    # 提取指定层的权值矩阵
    weights = model.layers[layer_index].get_weights()[0]
    shape = weights.shape
    
    # 生成和权值矩阵等大小的网格坐标
    X = np.array(range(shape[1]))
    Y = np.array(range(shape[0]))
    X, Y = np.meshgrid(X, Y)
    
    # 绘制3D图
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    plt.title(plot_title, fontsize=20, fontproperties='SimHei')
    
    # 绘制权值矩阵范围
    ax.plot_surface(X, Y, weights, cmap=plt.get_cmap('rainbow'), linewidth=0)
    
    # 设置坐标轴名
    ax.set_xlabel('网格x坐标', fontsize=16, rotation=0, fontproperties='SimHei')
    ax.set_ylabel('网格y坐标', fontsize=16, rotation=0, fontproperties='SimHei')
    ax.set_zlabel('权值', fontsize=16, rotation=90, fontproperties='SimHei')
   

def regularizers_influence(X_train, y_train):
    for _lambda in [1e-5, 1e-3, 1e-1, 0.12, 0.13]:  # 设置不同的正则化系数
        
        # 创建带正则化项的模型
        model = build_model_with_regularization(_lambda)
        
        # 模型训练
        model.fit(X_train, y_train, epochs=500, verbose=1)
        
        # 绘制权值范围
        layer_index = 2
        plot_title = "正则化系数：{}".format(_lambda)       
        
        # 绘制网络权值范围图
        plot_weights_matrix(model,layer_index, plot_title)
        
        # 绘制不同正则化系数的决策边界线        
        xx = np.arange(-2, 3, 0.01)        
        yy = np.arange(-1.5, 2, 0.01)
        
        # 生成 x-y 平面采样网格点，方便可视化
        XX, YY = np.meshgrid(xx, yy)
        preds = model.predict(np.c_[XX.ravel(), YY.ravel()])
        title = "正则化系数：{}".format(_lambda)
        
        make_plot(X_train, y_train, title, XX, YY, preds)
        

# 正则化的影响
regularizers_influence(X_train, y_train)