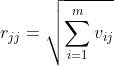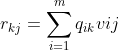改进的格拉姆-施密特正交化（modified Gram-Schmidt Process）

        最近在重新学习线性代数，学习的教材是MIT Gilbert Strang 教授的《INTRODUCTION TO LINEAR ALGEBRA》，在第4.4章节格拉姆-施密特正交化时，书中章节末尾介绍了一种改进的格拉姆-施密特正交化方法，但书中给出了公式，省略了很多细节，给学习理解造成了一定的难度，为自己今后或者遇到同样问题的朋友记录一下公式的来由。

        首先，介绍一下格拉姆施密特正交化的思想和方法。介绍正交化还得说说投影矩阵，我们在用最小二乘法解方程组的最优解的时候，由于Ax=b,b一般情况下，b并不一定存在于A的列空间中，这种情况下Ax=b其实是无解的，因为找不到列空间内合适的线性组合使其结果为b。这是后最小二乘法就派上用场了，最小二乘法的思想是，既然Ax=b无解，我们在列空间内找到一个向量p,下面这个方程组一定有解,那么怎么寻找p呢,最小二乘选取的p是使得||e||=||b-p||误差最小的那个p,其实这个p就是b在A的列空间上的投影。前面说了那么一大堆就是为了引出投影，那这个投影是怎么做呢，推导这里我就省略了，直接给出投影矩阵P：

        在线上的投影矩阵,这是后a是线上的向量：

        在子空间上的投影矩阵：。

        知道投影矩阵之后，那么为什么要正交化呢，有什么好处呢？投影矩阵中包含，使得普通的投影矩阵并不是那么漂亮，这一向给求解带来了很大的麻烦，那么能不能消除它呢？答案就是找到A列空间的一组标准正交基Q，因为对于标准正交基有如下性质，如果我们能找到列空间的标准正交基（格拉姆-施密特正交化要做的事情），那么上面的投影矩阵P中A用Q代替，表达式变为：,神奇的发现投影矩阵中不好的部分不见了。这也是标准正交令人着迷的地方。那么怎么寻找标准正交基呢，我们知道一个向量子空间中有多种可能的标准正交基，格拉姆-施密特就为我们提供了一种寻找标准正交基的方法，思想很简单：假设矩阵M=( a b c），A列空间的第一列为第一个标准正交基向量的方向，令A=a，通过除去向量的模得到第一个基向量，那么第二基向量怎么求呢，答案就是通过投影得到在A上的投影,根据投影的知识知道这是后有是垂直于的，那么我们得到第二个基向量，如果M矩阵还有第3个列向量，那我们如何得到呢？思想和得到的思想一样，对在和上做投影得到,, 重复第二步骤就可以得到所有的n个正交基向量，这就是格拉姆-施密特正交化。

        格拉姆-施密特正交化是A的一个因子分解，叫QR分解，A=QR，Q就是格拉姆-施密特正交化的标准正交矩阵，R是一个上3角矩阵，假设M=( a b c）,M的QR分解是如下形式：

        

        为什么R会是这样的上3角矩阵呢，原因是格拉姆-施密特正交化的过程，a在和方向一致，所以在上投影为0，同样b只在上有分量在上没有分量，格拉姆-施密特正交化的过程保证了A前面的列不会在后面的正交向量方向有分量，因为后面的正交分量始终是垂直于前面的列构成的向量子空间，也就是说与前面的列向量都垂直。下面我们推导一下就是b在方向投影的模长，这对后面理解改进的格拉姆-施密特正交化至关重要。

        b在上的投影由线上的投影矩阵知道:

       ,,可以推论R中其他项也是对于的向量在正交基向量上投影的模长。

        前面的准备知识够了，接下来，我们可以搬出改进的格拉姆-施密特正交化的公式了A是mxn阶矩阵:

           

             

        下面的公式从开始计算在上的模长（在上的模场由已经求得）：

       

             

        改进的格拉姆-施密特正交化就是上面的4个公式，下面我们就分析下这四个公式各自的含义：

        就是QR分解中R对角线上的值，如果对应上面举例的QR分解，那么,前面已经证明了R中的项是对应向量在正交基向量上投影的模长，是在方向上的投影，的表达式对应的正是在方向上的投影的模长。

        是的第j个元素值，来源于前面的格拉姆-施密特正交化,,。

        是QR分解中对角线之外的元素表达式，像的向量内积展开，这里有个小小的拐弯要知道，原来R矩阵第j列的元素对应的是，而这里通过迭代计算的方式，第一步，与元表达式一致，但是从第二次迭代开始，由第四个公式知道，这时,这时候的,因为,从几何上理解与正交，在上的分量不会对在上的分量的模长产生贡献，或者说在上的分量在上的投影为0，在计算到的投影时，可以先将在上的分量减掉。

        就是在迭代过程中从减去前面计算过的方向分量的剩余补向量。

        下面我们用改进的施密特正交化做一下上面介绍施密特正交化对M=(a b c)矩阵做的事情，直观的看看它和标准的施密特正交化的不同之处：

         

       

       

        摘抄一段书上改进的格莱姆-施密特正交化的matlab代码：

         for j=1:n                      %modified Gram-Schmidt
             v=A(:,j);                  %v begins as column j of A
             for i=1:j-1               %columns up to j-1, already settled in Q 
                 R(i,j)=Q(:,i)'*v;   %compute  
                 v=v-R(i,j)*Q(:,i); %subract the projection  
             end                        %v is now perpendicular to all of 
             R(j,j)=norm(v);       %diagonal entries of R 
             Q(:,j)=v/R(j,j);         %normalize v to be the next unit vector q_{j}
         end