WSDM 21-Temporal Cross-Effects in Knowledge Tracing
Temporal Cross-Effects in Knowledge Tracing
主要内容
- Temporal Cross-Effects in Knowledge Tracing
-
- Abstract
- 1 Introduction
- 2 Related Work
-
- 2.1 Knowledge Tracing
- 2.2 Temporal Dynamics in Knowledge Tracing
- 2.3 Hawkes Process
- 3 Empirical Study
-
- 3.1 Knowledge Tracing Task Setup
- 3.2 Dataset Description
- 3.3 Temporal Cross-Effects
- 4 Methodology
-
- 4.1 Preliminaries about Hawkes Process
- 4.2 HawkesKT Model
-
- 4.2.1 Base Intensity.
- 4.2.2 Temporal Cross-Effects.
- 4.3 Reparameterization Method
- 4.4 Parameter Learning
- 4.5 Prerequisite Score
- 5 Experiments
-
- 5.1 Experimental Settings
-
- 5.1.1 Datasets
- 5.1.2 Evaluation Protocols
- 5.1.3 Baseline Methods
- 5.1.4 Parameter Settings
- 5.2 Overall Performance
- 5.3 Efficiency Analyses
- 5.4 Ablation Study
- 5.5 Skill Relationships Discovery
- 6 Conclusion and Future work
Abstract
知识追踪(KT)旨在根据学生的历史表现建立学生的知识水平模型,这在计算机辅助教育和自适应学习中发挥着重要作用。最近的研究试图将过去互动的时间效应考虑在内,如遗忘行为。然而,现有的工作主要依靠与时间有关的特征或全局衰减函数来模拟时间敏感的影响。不同的跨技能影响的细粒度的时间动态还没有得到很好的研究(被称为时间交叉效应)。例如,对某些困难技能的交叉影响可能会迅速下降,而由不同的先前互动引起的影响也可能有不同的时间演变,这不能以全局的方式来捕捉。
在这项工作中,我们研究了KT中不同技能之间细粒度的时间交叉效应。我们首先通过实证研究验证了现实世界数据集中时间交叉效应的存在。然后,我们提出了一个新的模型–HawkesKT,在点过程的启发下对时间交叉效应进行了明确的建模,在这个过程中,以前的每一次互动都会对目标技能的掌握产生不同的时间敏感影响。HawkesKT采用了两个部分来模拟时间交叉效应。1)相互激励代表交叉效应的程度;2)核函数控制适应性的时间演变。据我们所知,我们是第一个在KT中引入Hawkes过程来模拟时空交叉效应的。在三个基准数据集上进行的广泛实验表明,HawkesKT优于最先进的KT方法。值得注意的是,我们的方法还表现出优秀的可解释性,并在训练效率方面显示出显著的优势,这使得它在现实世界的大规模教育环境中更加适用。
1 Introduction
如今,计算机辅助学习(CAL)已经成为教育方法学的一个重要组成部分。学生越来越容易在各种智能辅导平台上学习。此外,CAL系统中丰富的学习日志使其能够通过分析学生的学习历史数据提供个性化的学习轨迹。太难的技能或已经掌握的技能可以被识别出来,只有最适合的学习材料才会被呈现出来[31]。
学习者数据分析的一个关键问题是评估学生的知识状态。知识追踪(KT)就是这样一项任务,根据学生过去在教育应用中的互动,预测他们未来的表现(对评估问题的反应)[6]。由于学习过程中涉及许多因素,如一个人获取知识的能力、时间动态和人类的认知,所以它具有挑战性[29]。一些传统的方法使用隐马尔可夫模型来捕捉学生的知识演变过程,其中最流行的方法是贝叶斯知识追踪(BKT)[6, 15]。另一条工作路线围绕着项目反应理论(IRT),其目的是学习共同因素来概括观察结果[3, 16, 27]。最近,随着深度学习的快速发展,一些基于RNN的方法[24, 29]被提出来,以模拟相互作用之间的长依赖关系。
在这项研究中,我们想解决的是,学习是一个动态过程,在KT中存在时间交叉效应。首先,对一项技能的掌握不仅受以前同一技能的交互影响,而且还受其他技能的影响(交叉效应)。另一方面,不同的交叉技能效应的时间演变也可能是不同的。如图1所示,每个先前的互动都会对目标技能产生不同的直接影响。此外,虽然这种影响都会随着时间的推移而衰减,但它们的衰减速度是不同的,我们在本文中称之为时间性交叉效应。有些技能可能太容易被遗忘,而不同的先前互动所造成的影响也可能有不同的时间演变。
最近有一些研究开始部分解决KT中的上述时间性因素[11, 14, 24, 30, 37]。这些方法主要集中在将时间离散成片段或提取手工制作的特征。一些研究向前迈进了一步,使用全局衰减函数来控制遗忘行为[11, 14]。然而,如上所示,学习是一个适应性和动态的过程。之前的每一次互动都会以不同的时间动态产生效果。KT中的时间交叉效应可能取决于以前的互动和目标技能,这不能以全局方式完全捕捉。
在本文中,我们首先通过实证研究验证了KT中时间交叉效应的存在。基于对现实世界数据集中学生互动对之间的相互信息的分析,我们发现不同的交叉技能效应的时间演变确实是不同的。然后,我们引入了点过程来适应性地模拟KT的时间交叉效应。我们提出了一个新的模型–HawkesKT,它受到Hawkes过程的启发,是点过程的一个变种,利用强度函数来模拟时间上定位的事件之间的相互激发。在KT场景中,基本事件依赖于每个互动的技能和反应。具体来说,为了预测一个人的目标技能的知识状态,历史上的互动的累积效应和它们随时间的演变都自然地被设计的强度函数所描述。此外,这种交叉效应和时间演变对于不同的历史互动和目标技能是独特的。协同过滤在这里也被用来降低计算所有技能对参数的高复杂性。与基于深度学习的最先进的方法不同,我们的模型中的参数是高度可解释的,可以用来自动发现技能之间的潜在关系。实际上,HawkesKT揭示了一个全新的KT方法分支,它与现有的各种方法不同。这项工作的主要贡献可以概括为以下几点:
- 我们通过对真实世界数据集的实证研究,提出了KT中的时间交叉效应。不同的交叉技能效应的细粒度时间演变应被考虑在内。
- 我们提出了一个新的模型HawkesKT来解决KT中基于点过程的时间交叉效应。据我们所知,我们是第一个将Hawkes过程引入这一领域的人。
- 在三个真实世界的数据集上进行的比较实验表明了HawkesKT的有效性。我们的方法还表现出很好的可解释性,并在训练效率方面有明显的优势
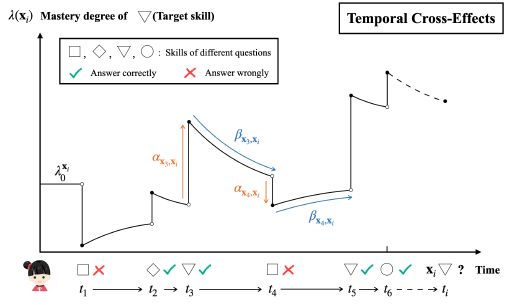
图1:说明目标技能的掌握程度(▽)如何受到时间交叉效应的影响。目标技能的基础知识水平表示为 λ x 0 i \lambda x^i_0 λx0i,每个过去的互动都会对目标技能的掌握程度产生适应性影响 ( α x j , x i ) (\alpha_{x_j ,x_i}) (αxj,xi)。此外,所有的影响都会随着时间的推移而发生变化 ( β x j , x i ) (\beta_{x_j ,x_i}) (βxj,xi),取决于以前的互动和目标技能。
2 Related Work
2.1 Knowledge Tracing
经典的是,关于KT的工作有两条线。一些研究是基于隐马尔可夫模型的。最具代表性的方法是BKT[6],它用一个二进制变量来描述学生的知识状态。另一条工作路线是基于因素分析的。IRT [12] 倾向于在观察测试反应的基础上假设和修改受试者的潜在特征。AFM[3]和PFA[27]是逻辑回归模型,根据以往不同的信息来预测成绩。此外,最近提出的KTM[34]利用因子化机器来模拟特征间的成对互动,并被证明包含了上述所有的因子分析模型。
随着深度学习在一系列领域的快速进展,RNN被利用来捕捉相互作用之间的复杂依赖关系。DKT[29]在每一步使用RNN的隐藏状态来表示学生的知识状态,并得到了普遍看好的结果。随后,许多研究遵循DKT来扩展其容量[5, 17, 32],一些工作试图探索其他模型结构(如记忆网络,自我注意)以获得更高的表现力[2, 25, 39]。然而,上述所有的方法都忽略了时间信息的重要性。因此,给定一个交互序列,他们不能准确估计学生在不同时间的知识变化状态。
2.2 Temporal Dynamics in Knowledge Tracing
通常情况下,KT中存在大量的时间信息,时间动态对预测未来反应的影响也逐渐显现出来。许多研究关注学习过程中的遗忘行为。早期的探索主要是将滞后时间因素纳入BKT或PFA[28, 30]。DKT-t[20]和DKTForgetting[24]在DKT中引入不同的基于时间的特征。DKT-Forgetting考虑了重复和序列的时间间隔,以及过去试验的数量,这是一种最先进的具有时间信息的方法。最近,一些工作利用衰减函数来控制遗忘行为[11, 14],它假设最近发生的互动有较大的影响。
然而,这些研究要么依赖手工制作的特征,要么用全局衰减率模拟持续变化的影响。不同的是,我们的HawkesKT明确地模拟了以前每次互动的时间交叉效应,这可以捕捉到不同交叉技能效应的明显时间趋势。
2.3 Hawkes Process
众所周知,点过程善于对时间上局部的连续事件进行建模[7]。点过程已经有很多应用,包括地震预测[21]、社交网络中的用户影响力[33, 40]和论文引用次数[38]。在点过程的变体中,Hawkes过程[13]明确地模拟了连续事件的自激和互激特征,相应的时间趋势由强度函数中的核函数控制。最近,Hawkes过程越来越受到人们的关注,并在各种领域显示出巨大的有效性,如在线活动预测和个性化推荐[8, 22, 35]。
3 Empirical Study
在这一节中,我们首先正式定义了知识追踪任务,并介绍了本文中使用的符号。然后,我们验证了在现实世界的教育数据集中是否存在时间交叉效应。
3.1 Knowledge Tracing Task Setup
定义3.1(知识追踪任务)。 给定学生的行动间序列{ = x0, x1, , x },知识追踪(KT)的目的是预测他/她在下一次互动x+1中是否能正确回答问题。
在本研究中,一个交互x被定义为一个元组( , , ),包括学生在时间戳尝试回答的问题,以及相应的响应 ∈ \in ∈ 0, 1(答案的正确性,1表示正确)。该序列按时间升序排序,即对于任何 < , < 。此外,为了识别每个问题所涉及的技能,我们有一个从问题到技能的映射(-),可以得到问题对应的技能ID ()。这里的+1是给定和(+1, +1)的预测目标。
3.2 Dataset Description
这里我们使用一个真实世界的基准数据集,ASSISTments 12-13,来进行实证研究。
ASSISTments 是一个在线辅导系统,用于教授和评估学生的数学,这一系列数据集经常用于相关研究[10]。数据集中共有 270 万次交互,涉及 265 项技能。更详细的信息可以在第 5.1.1 节中找到。
为便于理解,我们将主要展示频率最高的前 10 项技能的分析结果。表 1 显示了数据集中这些技能的名称。请注意,这些技能 ID 将在整篇论文中使用。

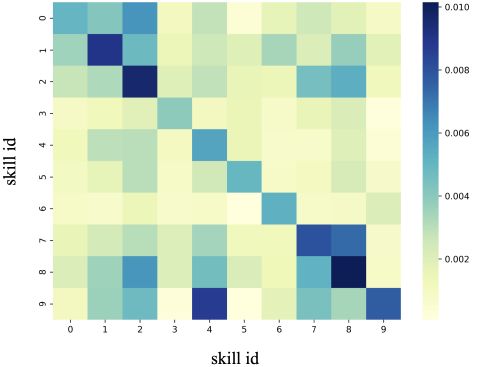
图 2:所有技能对的 CMI(交叉效应)。 y轴是前互动的技能id,x轴是后互动的技能id。
3.3 Temporal Cross-Effects
为了验证是否存在时间交叉效应,我们首先定义了学生交互对之间的条件互信息(CMI),它将用于以下分析。
定义 3.2(条件互信息)。给定一个限制条件 ,我们可以在每个学生的交互序列中找到满足 的所有交互对(x , x )。如果我们将交互前和交互后的响应( 和 )分别视为一个随机变量,则条件互信息定义为,
C M I ( a i ; a j ) = ∑ a i ∈ 0 , 1 ∑ a j ∈ 0 , 1 P ( a i , a j ) ⋅ l o g P ( a i , a j ) P ( a i ) P ( a j ) CMI(a_i; a_j) = \sum_{a_i \in {0,1}} \sum_{a_j \in {0,1}} P(a_i, a_j) · log \frac{P(a_i, a_j)}{P(a_i)P( a_j)} CMI(ai;aj)=∑ai∈0,1∑aj∈0,1P(ai,aj)⋅logP(ai)P(aj)P(ai,aj). (1)
这里的条件可以是前后交互的特定技能,或者两次交互之间的时间间隔。定义中的概率可以通过计算所有满足的交互对中的频率来推导出来。实际上,CMI 反映了限制条件下前交互和后交互之间的依赖程度。
首先,我们限制交互前和交互后的技能以验证技能之间的交叉影响。请注意,如果两个技能完全独立,则对应的 CMI 应为 0。图 2 显示了所有技能对组合的 CMI。 y轴是前互动的技能id,x轴是后互动的技能id。我们可以看到,对于相同技能(对角线)的交互,效果通常是最大的。但是,不同技能之间存在明显的交叉效应,例如前交互和后交互分别为9和4的情况。并且技能组 {0, 1, 2} 和 {7, 8, 9} 中的依赖性很高,这是有道理的,因为这些技能通常被认为是相关的。因此,在预测目标技能的掌握程度时,重要的是不仅要关注以前与相同技能的互动,还要关注其他相关的互动。
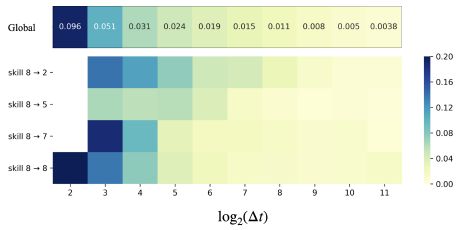
其次,我们继续研究不同交叉效应的时间演变。除了像之前一样限制交互前和交互后的技能,我们进一步根据两次交互之间的对数时间间隔对交互对进行分组。图 3 显示了全球趋势和一些具有代表性的技能对。对数转换后的时间间隔从 2 开始,一些网格被屏蔽,因为在这些条件下没有足够的交互对(小于 50)。从全球来看,由于遗忘行为,整体时间演化呈现衰减形式,这与之前的研究一致 [24]。然而,值得注意的是,对于不同的技能对,衰减率明显不同,我们称之为时间交叉效应。例如,前后交互分别为8和7时,短期内CMI较大,因为它们高度相关,但随时间衰减很快。
另一方面,8 和 2 之间的 CMI 较小且衰减较慢,这是合理的,因为技能 2 相对容易,并且这两个技能没有直接关联。请注意,还有许多其他技能对表现出显着差异,关于时间演化,在这种情况下,先前工作中的全局衰减函数是不够的。
因此,为了捕捉上述实证研究中显示的这种时间交叉效应,对 KT 中的细粒度遗忘行为进行建模非常重要,其中应考虑交叉技能效应和自适应衰减率。
4 Methodology
4.1 Preliminaries about Hawkes Process
从形式上看,时间点过程是一个随机过程,其实现由一列在时间上定位的离散事件组成,{}∈N,时间∈R+。在 KT 场景中,它代表了学生正确/错误地回答不同问题时的一系列时间戳,这构成了时 间点过程的基本事件。给定过去事件 的历史时间,时间点过程引入了条件强度函数 ( | ),表示下一个事件时间的随机模型。为了简单起见,我们在以下部分省略条件符号为()。那么, 在一个小的时间窗口[, + ]内发生新事件的概率可以表示为[1, 35]:
( ) = P{event in [, + ) | }。. (2)
至于强度函数()的具体形式,各种模型都有所不同。作为一种流行的、强大的变体,Hawkes过程对事件之间的激发进行建模,其强度函数的形式为:
( ) = 0 + ∑ t j < t \sum_{t_j < t} ∑tj<t ( - ) , (3)
其中 0 是基础强度,每个历史事件都有一个成瘾效应 。这些影响随时间间隔而变化,触发内核(-)控制相应的时间特征。
4.2 HawkesKT Model
受Hawkes Process中强度函数的启发,我们设计了 (x ) 来表示考虑到历史交互 ,学生在 正确回答问题 的可能性。 为了模拟 KT 中的时间交叉效应,使用互激励 x ,x 来捕获交叉技能效应,并且在设计的核函数 x ,x (·) 中解决了细粒度的时间演化,从而导致强度函数 形式如下:
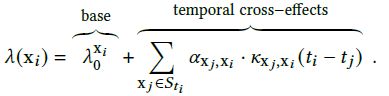
这里的总强度由基础强度x 0 和时间交叉效应部分组成。 基础强度旨在捕捉目标问题本身的难度,而时间交叉效应模拟先前交互的自适应时变影响。
4.2.1 Base Intensity.
我们注意到以前的研究通常没有考虑问题索引,可能是由于数据稀疏及其带来的大量参数。在基于深度学习的模型中,给每个问题一个单独的嵌入太昂贵了。因此,使用技能索引问题是避免过度拟合和过度参数化的有效方法。然而,在实践中,即使具有相同的技能,不同的问题也有不同程度的难度。缺乏问题的建模会导致表达能力和灵活性降低。
在这里,我们利用基础强度来捕捉技能和问题的难度,其定义如下:
![]()
其中 λ 0 q i \lambda_{0}^{q_i} λ0qi 和 λ 0 s ( q i ) \lambda_{0}^{s(q_i)} λ0s(qi)参数分别为分别是问题和技巧。在预测目标交互 x 的响应时,之前的每一次交互都会在这个基础强度 λ 0 x i \lambda_{0}^{x_i} λ0xi的基础上生效,它代表了目标交互的固有特征。这样,每个问题只引入一个参数,在建模单个问题和避免过度参数化之间取得平衡。
4.2.2 Temporal Cross-Effects.
如第 3 节所示,之前的事件对目标交互有不同的影响,并且影响会随着时间的推移而衰减。此外,衰减率彼此不同,这与历史交互和目标技能都有关。在这一部分中,我们专注于对 KT 中的这种自适应时间交叉效应进行建模。这里主要有两个组成部分:(1)相互激励 x ,x 控制即时效应的程度,以及(2)核函数 x ,x ( − ) 控制交叉效应的细粒度时间动态。
首先,我们使用 x ,x 来建模之前的交互 x 会在多大程度上影响目标交互 x 中的响应。这里我们将技能-响应对 ( ( ), ) 视为历史序列中的一个基本事件, 技能指数 ( ) 是目标会受到影响2。这样,假设有|S|综上所述,互激励 x ,x 可以解析为形状为 2|S| 的参数矩阵× |S|。第一个维度代表历史交互的状态,第二个维度代表要预测的目标技能。值得注意的是,互激励x ,x 内在地包含了每个技能对之间的关系。
其次,为了对遗忘行为建模,我们选择使用指数函数作为核函数: 6) 其中 x ,x 是另一个控制不同情况下细粒度衰减率的核心参数。具体来说,给定目标技能,具有不同技能和反应的历史事件的影响将具有自适应衰减率。至于核函数的形式,指数函数是逼近遗忘曲线的自然选择。它也常用于霍克斯过程的许多应用中,并且在大多数情况下被证明是有效的 [9, 23, 38]。此外,我们发现对时间间隔 − 应用对数变换很重要,因为时间间隔通常表现出长尾分布。在这个设置下,指数函数实际上变成了幂函数 1/( − ) 1+x ,x。还可以设计其他功能形式以适应不同的实际应用场景。
随后,使用强度值 (x ),通过将 sigmoid 函数应用于强度值来预测在交互 x 中正确回答问题的概率: ˆ B ( = 1) = 1 1 + exp(−(-) x )) . (7)
4.3 Reparameterization Method
接下来,我们重点讨论如何处理我们模型中的参数。除了基础强度,核心参数是 x ,x 和 x ,x。通常,它们在 Hawkes 过程中分别建模为矩阵,其中每个条目表示历史和目标事件的特定组合的参数:A ∈ R2|S|×|S|,B ∈ R2|S|×|S| , (8) 第一个维度代表技能-响应对( ( ), ),第二个维度索引目标技能 ( ) 进行预测。
虽然直接优化参数矩阵是一个直观的解决方案,但存在两个主要问题。首先,与总共 2|S|2 种组合相比,数据集中存在的事件对通常是稀疏的。结果,只有少数参数会被更新,如果|S|,参数的数量会很大。很大。其次,不同对的参数是独立的,因此从数据中学到的时间交叉效应的模式不能传播以及推广到看不见的情况。因此,我们引入矩阵分解作为重新参数化方法,以利用协同过滤 [19] 并减少推荐系统中经常使用的参数总数 [4, 36]。
2我们不使其特定于问题,因为这将太细粒度而无法学习有意义的相互参数,而技能则是更合适的水平。
协同过滤假设相似的历史事件对目标交互具有相似的影响。我们可以将技能-反应对和目标技能编码到相同的向量空间中,并使用内积导出每个组合的参数。这样,我们将为每组核心参数有两个因子矩阵:P∈R2|S|×,Q∈R|S|×,P∈R2|S|×,Q∈R|S| ×。
这里 表示隐藏空间的维度。那么具体的 x ,x 和 x ,x 可以计算为: x ,x = Õ =1 ( |+) · ( ) , (9) x ,x = Õ =1 ( )+ | · ( ) . (10)
这样,考虑到≪|S|,参数的数量将从(4|S|2)减少到(6|S|)。此外,受益于协同过滤,时间交叉效应的学习模式被编码在每个维度的嵌入中。这对于模拟罕见交互对的时间交叉影响和理解技能之间的潜在关系非常有帮助。
4.4 Parameter Learning
综上所述,HawkesKT 中的参数是基础强度 0 、 ( ) 0 和因子矩阵{P,Q, P,Q}。为了共同学习这些参数,我们优化了预测概率 ˆ+1 和真实响应 +1 之间的标准交叉熵损失:
L = − Õ (+1 logˆ+1 + (1 − +1 log) (1 − ˆ+1)) (11)
由于Adam算法[18]的成功,我们使用Adam作为学习算法。我们还在因子矩阵上添加了权重衰减。
4.5 Prerequisite Score
除了预测未来的表现,HawkesKT 还能够根据有意义的参数自动发现潜在的技能关系。请注意,参数 x ,x 本质上包含技能之间的相互影响。我们将{1,1},2 表示为使用技能1 正确回答问题对目标技能2 的影响。同理,{1,0},2 表示1 不正确的情况。
直觉上,如果1是2的先决条件:(1)1的低知识水平会对2产生负面影响; (2) 对2 的高度掌握可能表明对1 很了解。相应地,{1,0},2 应该很小,而{2,1},1 应该很大。因此,对于每个技能 ,我们定义其先决条件分数 ( ) ∈ R|S|表示其他技能是 的先决条件的可能性: ( ) = softmax { ,1}, softmax {,0}, , (12) 旨在使 softmax 正常化所有技能之间的效果。
然后给定任何技能 ,我们可以根据先决条件分数 ( ) 得到它最可能的先决条件。
在当前的教育文献中,技能之间的关系通常是人工标注的,这需要大量的资源和时间。所提出的方法可以作为教育专家的参考和补充,这对于在线教育场景和传统课堂教学都具有重要意义。技能关系发现的结果将在第 5.5 节中介绍。
5 Experiments
5.1 Experimental Settings
5.1.1 Datasets
我们使用三个真实世界的数据集来验证我们模型的有效性。
• ASSISTments 09-10。 [10] ASSISTments 是一个在线辅导系统,用于教授和评估学生的数学。
该数据集是公开可用的。
• ASSISTments12-13。该数据集来自与以前相同的系统,但具有不同的时间跨度。
• slepemapy.cz。 [26] 该数据集来自用于练习地理的在线系统,并且是公开可用的。我们使用 place_asked 作为技能标识符。每个技能根据类型会有两个问题:(1)在地图上找到给定的地方; (2) 为突出显示的地方选择名称。
对于每个数据集,我们丢弃少于 5 次交互的无效用户,只考虑每个用户的前 50 次交互,因为在用户历史很少时预测性能更为重要。此外,ASSISTments 09-10 中缺少每次交互的时间戳,因此我们假设用户以固定的时间间隔(1 秒)连续回答问题。预处理后,三个数据集的统计数据如表2所示。
5.1.2 Evaluation Protocols
我们执行 5 折交叉验证来评估所有模型,其中根据用户分割折叠。通过从训练集中提取 10% 的用户来构建验证集,用于调整超参数和执行提前停止。对于每个序列,除了第一个位置之外的每个位置都将用于训练和评估。我们使用曲线下面积(AUC)作为评估指标。之前的许多研究也采用了上述设置 [24, 29]。
5.1.3 Baseline Methods
我们在不同方面将我们的 HawkesKT 模型与六种基线方法进行了比较。前三个基线不包含时间信息:
• IRT [16]。这是一种基于项目响应理论的传统方法,它使用两组参数对项目和用户的特征进行建模。
• DKT [29]。 DKT 通过 RNN 的隐藏状态来表示学生的知识。每个技能都被编码为一个one-bot向量或低维嵌入。
• SAKT [25]。这是最近提出的一种基于自注意力机制的深度学习方法。
其余三个基线考虑了时变效应:
• DKT-Forgetting [24]。这是一个基于 DKT 的模型,将过去的试验和时间间隔视为额外特征。
• KTM [34]。该方法利用因子分解机对特征之间的交互进行建模。这里我们使用的特征包括问题 id、技能 id、不同技能的历史反应以及 DKT-Forgetting 中的时间特征。
• AKT-R [11]。这是一个基于注意力的神经网络模型,注意力权重是通过具有全局衰减率的距离感知指数衰减来计算的,这是一种具有时间信息的最先进方法。
我们不包括基于 BKT 的方法,因为它们已经包含在上述方法中。
5.1.4 Parameter Settings
我们在 PyTorch 中实现了 HawkesKT 和其他基线(IRT 除外),并且代码是公开的。为了公平比较,所有数据集上不同模型的嵌入大小和隐藏大小固定为 64。如果验证集上的 AUC 在 5 个时期内没有增加,则应用提前停止。学习率在 {5−3, 1−3, 5−4, 1−4} 之间调整,l2 系数在 {1−3, 1−4, 1−5, 1−6, 0} 之间调整.所有模型参数通常初始化为 0 均值和 0.01 标准差。
5.2 Overall Performance

Table 3: 所有方法在三个数据集上的AUC(越高越好)。我们进行5倍交叉验证,并报告平均得分。最好的结果以粗体字显示,最好的基线以下划线显示。*和**表示我们的方法明显优于相应的基线,分别为 < 0.05 和 < 0.01。
表 3 显示了所有基线方法和我们的 HawkesKT 模型的性能。我们有以下观察结果:
首先,不同类型的基线表现出明显的性能差距。作为基于 RNN 的模型,DKT 优于传统的 IRT。我们还发现 DKT 在所有数据集上都优于 SAKT,这与之前的工作 [11] 一致。 DKT-Forgetting 获得进一步改进,表明考虑时间因素的重要性。 KTM 可以灵活地结合问题级别和时间特征,因此有时比基于 DKT 的模型表现更好。大多数情况下,AKT-R 会产生显着的结果,因为它不仅对时间衰减进行建模,而且还通过基于 Rasch 模型的嵌入包含问题级别信息。但是我们发现 KTM 和 AKT-R 由于模型容量大,在训练过程中容易过拟合。
其次,HawkesKT 的表现始终优于所有基线。与DKT-遗忘相比,HawkesKT自然会考虑到连续时变的效果,而不仅仅依赖于同技能或相邻技能的互动。KTM 能够扩展以合并时间特征,但它需要手工制作的特征,并且无法捕获每个先前交互的自适应时间交叉效应。至于 AKT-R,虽然它结合了指数衰减来模拟遗忘行为,但衰减率仍然是全局的。因此,它无法捕捉到这项工作中揭示的时间交叉效应,从而导致性能欠佳。相反,我们的 HawkesKT 模型通过相互激励和自适应核函数来解决时间交叉效应,从而始终获得最佳结果。
第三,我们的 HawkesKT 模型能够扩展到不同的场景。这三个数据集涉及不同的主题,数据规模从小到大。一致的改进证明了 HawkesKT 的可扩展性。请注意,我们的模型在数学数据集上获得了更多改进。而在地理数据集 (slepemapy.cz) 上,改进并不大(与 DKT-Forgetting 相比差异不显着)。这是合理的,因为技能之间的时间交叉效应确实对数学更有帮助。至于地理,一般只有周边国家才能帮助确定目标国家。技能之间的关系很简单,主要的时间动态是自我遗忘,这就是为什么 DKTforgetting 和 AKT-R 表现良好的原因。
5.3 Efficiency Analyses
作为方法的一个新分支,我们还研究了 HawkesKT 的效率问题。表 4 显示了两个代表性数据集上不同方法的每个 epoch 的训练时间和参数总数。我们确保在相同的实验设置(批量大小、嵌入大小、最大序列长度)下评估所有方法。所有实验均使用单个 1080Ti GPU 进行。
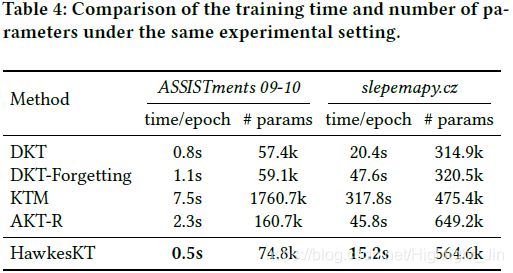
我们可以观察到 HawkesKT 的训练时间比其他最先进的方法少得多,甚至比 DKT 还要快。KTM特别慢,如果数据集中的问题很多,就需要丰富的参数。 ART-R 也因为其复杂的模型结构而效率不高。值得注意的是,与最近的工作相比,我们的 HawkesKT 不仅参数更少,而且在实现最佳性能的同时大幅降低了训练成本。在真实的教育场景中,及时性也是一个重要因素。 HawkesKT 在有效性和效率方面的显着优势将使其更适用于现实世界的大规模教育环境。
5.4 Ablation Study
为了验证建模时间交叉效应的影响,我们将 HawkesKT 与三个变体进行比较:
• \Temporal:该模型移除了核函数,因此不考虑遗忘行为,导致强度函数如下: (x ) = x 0 + Í x ∈ x ,x .
• \Cross:该模型使用全局参数 来控制指数衰减: (x ) = x 0 + Í x ∈ x ,x -log
• \CF:该模型不使用矩阵分解作为重新参数化方法,直接优化参数A、B,形状为2|S| × |S|。
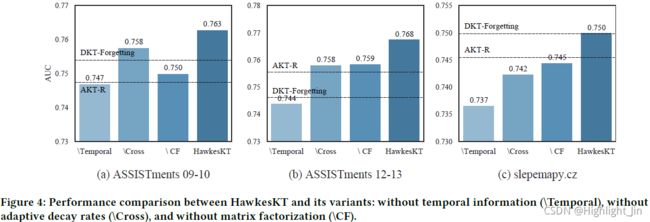
图 4 显示了 HawkesKT 及其变体在所有数据集上的 AUC,以及用于比较的 DKT-Forgetting 和 AKT-R。我们有以下主要观察结果:
首先,时间信息在 KT 中非常重要。\Temporal 导致最大的性能损失,通常比 DKT-Forgetting 和 AKT-R 更差,这表明需要对遗忘行为进行建模。
其次,重要的是对具有不同衰减率的细粒度时间演化进行建模,以捕获 KT 中的时间交叉效应。
尽管 \Cross 的性能损失不是最大的,但值得注意的是 \Cross 导致在所有数据集上的结果始终更差。在没有时间交叉效应的情况下,\Cross 在 ASSISTments 12-13 上使用 AKT-R 产生类似的结果。这表明全局衰减率是不够的,我们模型中解决的自适应时间交叉效应确实有帮助。
第三,使用矩阵分解的重新参数化带来了稳定的性能增益。矩阵分解有助于利用协同过滤,这使学习到的模式能够通过嵌入传播并在不同情况下进行泛化。在没有矩阵分解的情况下,\CF 在所有数据集上的性能都会遭受中等损失,这表明结合点处理和协同过滤的有效性。
5.5 Skill Relationships Discovery
这里我们想验证一下基于第4.5节中提出的先决条件得分的关系发现的性能。
首先,我们利用在ASSISTments 12-13上训练的参数与前10个频率技能作为案例研究。我们在图5中直观地展示了一些代表性技能之间的关系。圆圈代表技能,箭头代表技能之间的先决条件关系。计算出的先决条件分数也被标注在箭头旁边(箭头越粗,关系越强)。带颜色的圆圈是我们关注的代表性技能,它的主要先决条件以及它们之间的关系被画了出来。该图显示,我们的模型确实发现了一些有意义的关系。例如,所有运算顺序(红色为6)依赖于关于加/减(2)和乘/除(7,8)的技能。乘/除法技能的先决条件分数较高,因为在确定运算顺序时,这些技能更为重要。此外,乘法分数(7)是除法分数(蓝色为8)的有力前提,加减法分数(2)也有一定影响。
其次,我们进行了一个注释实验来定量验证所发现的关系。我们选择ASSISTments 12-13中的前20个频率技能,请三位专家对每个技能对之间的二元帮助性进行注释。注释的卡帕系数为0.52,显示了其适用性。平均的注释结果被用作相关性的基础真理。然后,根据提议的先决条件得分,为每个技能生成一个排名列表。这个排名列表根据注释的相关性进行评估,其平均NDCG为0.8267。这表明我们的模型确实能够自动找到与人类认知一致的技能之间的关系。
上述分析验证了我们的参数化假设,并证明HawkesKT中的参数是高度可解释的。揭示的关系图可以作为教育专家的有效完成。这种方法还可以扩展到寻找大量技能之间的关系,这对在线和传统教育场景都有帮助。
6 Conclusion and Future work
在本文中,我们建议对 KT 中的时间交叉效应进行明确建模,这意味着不同交互之间的自适应时变效应。通过实证研究,我们验证了不同的跨技能效应具有不同的时间动态。基于数据中显示的时间交叉效应,提出了一种新的基于点过程的模型 HawkesKT,它揭示了 KT 方法的一个新分支。在 HawkesKT 中,每个历史交互都会对目标技能产生自己不断变化的影响,由相应的核函数控制。与最先进的方法在不同场景中的三个真实世界数据集上相比,所提出的 HawkesKT 实现了卓越的性能。同样值得注意的是,我们的模型在训练效率和参数可解释性方面显示出显着优势。我们进一步提出先决条件分数,以根据我们模型中的参数自动发现潜在的技能关系,可以作为教育专家的参考和完成。
未来,我们计划为 HawkesKT 启用可扩展的边信息,因为当前模型不够灵活,无法考虑其他特征,例如学校、问题类型等。我们还考虑结合技能之间的已知依赖关系来提高预测性能。