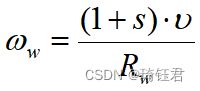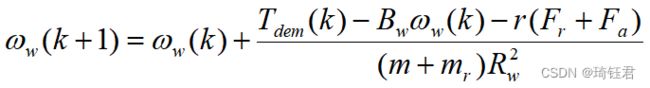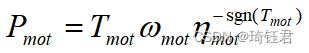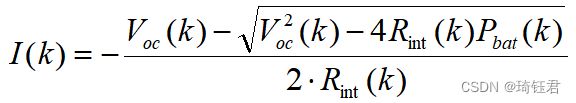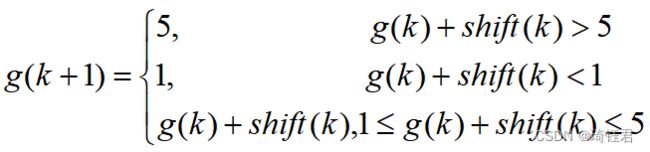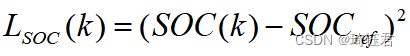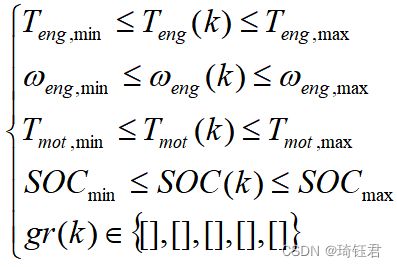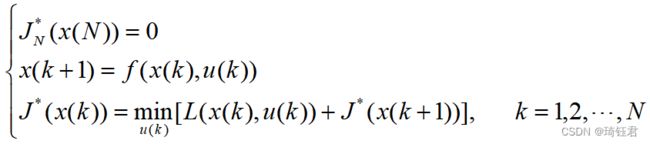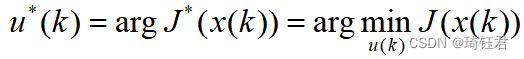基于动态规划的并联式混合动力汽车全局最优能量管理策略研究
目录
0 引言
1 并联式混合动力汽车系统构型
1.1动力系统构型
1.2车辆模型
2 基于动态规划的能量管理策略
2.1 能量管理最优问题提出
2.2 基于动态规划的能量管理策略求解
3 仿真实验及结果分析
4 结论
0 引言
混合动力汽车由于兼具传统燃油汽车和纯电动汽车的优点,在纯电动汽车和燃料电池汽车技术尚未成熟及充电等基础设施未普及之前,成为了各国政府和汽车行业关注的重点。能量管理策略作为HEV的核心技术之一,是车辆具有良好性能的基础,其核心是解决发动机和电机在各种行驶工况下的功率分配问题。本项目以P2构型的并联式混合动力汽车为研究对象,选取代表驾驶环境的标准工况,以油耗最小为目标函数,同时考虑驾驶舒适性,利用DP算法求解标准工况下全局最优控制策略,并利用MATLAB/Simulink平台对控制策略进行了仿真验证。
1 并联式混合动力汽车系统构型
1.1动力系统构型
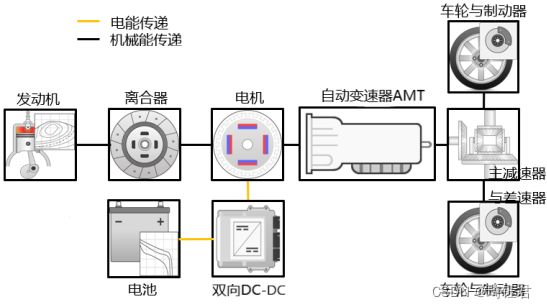
本项目研究的混合动力电动汽车为一单轴并联式混合动力汽车,其动力系统结构如图1 所示。该并联式 HEV 的动力总成系统主要包括发动机、电机、离合器、传动系及电池。其中,电机直接与离合器的输出和传动系的输入相连。电机转子同时作为转矩耦合器直接使用。因此,省略了机械耦合器,这种车辆动力总成系统结构简单紧凑。这种结构中,电机有发动机启动器、回馈制动中的发电机以及发动机辅助三个功能。这种车辆模型可以在发动机单独驱动、电机单独驱动、混合驱动和回馈制动四种模型下自由切换工作。
1.2车辆模型
车辆动力系统建模是理解车辆运行规律的第一步。选择能代表车辆动力学和动力系统关键部件特征的参数,准确反映车辆运行规律;同时,减少不必要的参数使用量,提高模型的运算时间。准确的HEV动力学模型可以提高能量管理算法的精度。由于能量管理策略设计与车辆纵向速度正相关,而与车辆其他方向的速度无关,本项目忽略了车辆的横向动力学特性和驾驶稳定性,仅根据车辆纵向动力学来对车辆运动进行建模。在车辆纵向动力学模型中,给定车速![]() 和坡度
和坡度![]() ,驾驶员需求转矩为:
,驾驶员需求转矩为:
|
|
(1) |
其中,![]() 为空气密度;
为空气密度; ![]() 为整车总质量;
为整车总质量;![]() 为滚动阻力系数;
为滚动阻力系数;![]() 为车速;
为车速;![]() 为空气阻力系数;
为空气阻力系数;![]() 为迎风面积;
为迎风面积;![]() 为道路坡道角;
为道路坡道角;![]() 为旋转质量换算系数;
为旋转质量换算系数;![]() 为车轮半径。
为车轮半径。
由车辆的转矩耦合规律与变速传动特点可以得到变速箱输入口的需求转矩![]() 为:
为:
| (2) |
其中,![]() 为变速器档位减小引起的损耗,本文中假定为 0;
为变速器档位减小引起的损耗,本文中假定为 0;![]() 为加速主减速器的惯性转矩,本文中假定为 0;
为加速主减速器的惯性转矩,本文中假定为 0;![]() 为变速器内齿轮档数;
为变速器内齿轮档数;![]() 为变速器速比;
为变速器速比;![]() 为主减速驱动轴主减速器速比。同时,
为主减速驱动轴主减速器速比。同时,
| (3) |
其中,![]() 和
和![]() 分别为发动机转矩和电机转矩。
分别为发动机转矩和电机转矩。
车轮角速度![]() 与车轮线速度
与车轮线速度![]() 的关系为:
的关系为:
| (4) |
其中,![]() 为轮胎滑移率。
为轮胎滑移率。
车轮角速度![]() 与变速器输入口的角速度
与变速器输入口的角速度![]() 、电机角速度
、电机角速度![]() 的关系为:
的关系为:
| (5) |
且,
| (6) |
其中,![]() 为电机角速度。
为电机角速度。
由车辆运动方程可以总结出:
| (7) |
其中,![]() 为空气粘度系数;
为空气粘度系数;![]() 为滚动阻力;
为滚动阻力;![]() 为空气阻力;
为空气阻力;![]() 为车辆旋转部件的等效平移质量。同时,
为车辆旋转部件的等效平移质量。同时,
| (8) |
其中,![]() 为传动系统的转动惯量输入,
为传动系统的转动惯量输入,![]() 为车轮的转动惯量。
为车轮的转动惯量。
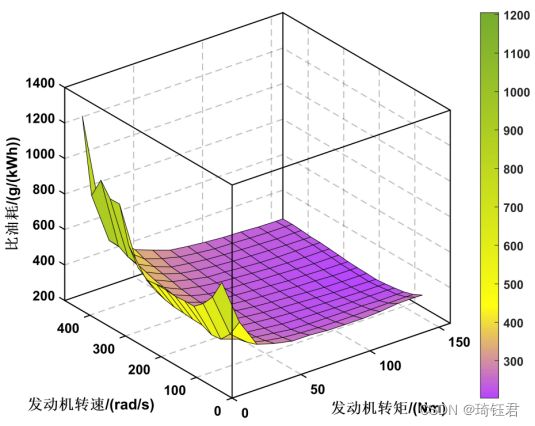
本项目基于准静态原理,对并联 HEV 动力总成系统的关键部件:发动机、电机、电池、变速箱和离合器进行建模。假定发动机已完全预热,忽略发动机的启动过程、停止过程以及温度对其影响。不考虑发动机的怠速模式。即认为发动机输出转矩为 0 时,发动机是处于关闭状态。根据发动机运行的历史数据,建立发动机(转速,转矩,燃油消耗率)表格。图2为建立的燃油消耗率随发动机转速和转矩的变化图。在实际使用中,可以根据发动机转速和转矩的二维插值函数得到实际的。 单位有效功的耗油量可表示为
| (9) |
其中,![]() 为比油耗,可通过一定转速和转矩查找准静态发动机万有特性MAP图得到。
为比油耗,可通过一定转速和转矩查找准静态发动机万有特性MAP图得到。
本项目忽略电机的电磁特性,电机功率由下式给出:
| (10) |
其中,![]() 为电机效率,可通过一定转速和转矩查找电机准静态效率MAP图得到。电机工作在制动能量回收时,为电磁效率的导数。当
为电机效率,可通过一定转速和转矩查找电机准静态效率MAP图得到。电机工作在制动能量回收时,为电磁效率的导数。当![]() 时,电机工作在电动模式;当
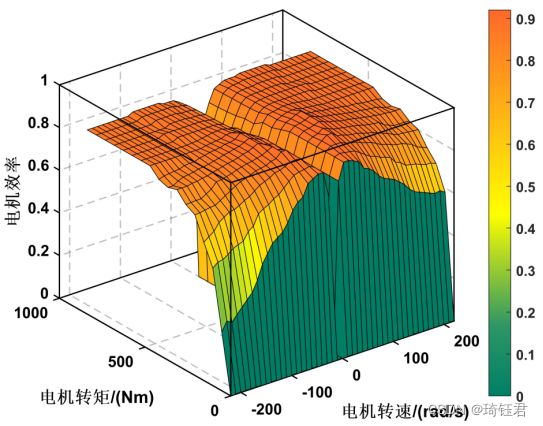
时,电机工作在电动模式;当![]() 时,电机工作在制动回收模式。另外,我们结合实验数据和电机动力学(机械特性),将电机效率表示为电机转矩和电机速度的静态函数。图3为电机效率随电机转矩和转速的变化图。
时,电机工作在制动回收模式。另外,我们结合实验数据和电机动力学(机械特性),将电机效率表示为电机转矩和电机速度的静态函数。图3为电机效率随电机转矩和转速的变化图。
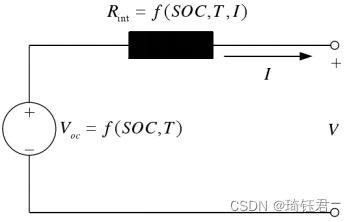
本项目忽略温度和老化对镍氢电池的影响,采用等效的内阻模型对电池组进行建模。
根据上述电池模型,可以得到电池的充放电电流如下:
| (11) |
其中,![]() 为电池开路电压;
为电池开路电压;![]() 为电池内阻;
为电池内阻;![]() 为
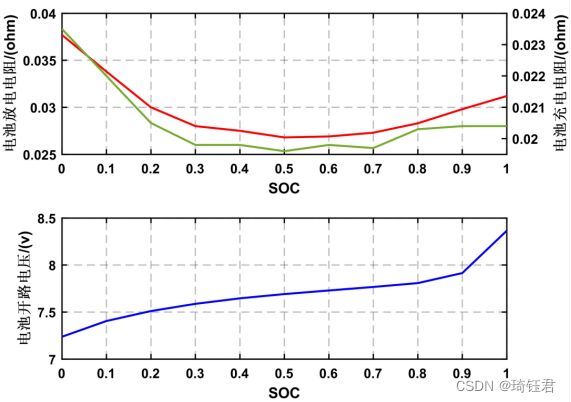
为![]() 时刻电池为电机提供的功率。电池放电时,其值为正;电池充电时,其值为负。图5为单体电池充电电阻、开路电压与电池荷电状态SOC的关系图以及单体电池充放电电阻、开路电压与电池荷电状态的关系图。
时刻电池为电机提供的功率。电池放电时,其值为正;电池充电时,其值为负。图5为单体电池充电电阻、开路电压与电池荷电状态SOC的关系图以及单体电池充放电电阻、开路电压与电池荷电状态的关系图。
电池荷电状态SOC的变化公式为:
| (12) |
其中,![]() 为时间变化量;
为时间变化量;![]() 为最大容量。
为最大容量。
本项目将变速器的档位迁移被建模为一个离散时间动态系统,每次迁移持续的时间为 1 秒。
| (13) |
其中,状态![]() 表示
表示![]() 时刻为变速器内齿轮档数。
时刻为变速器内齿轮档数。 ![]() 表示
表示![]() 时刻的变速器档位迁移命令,分别用1,0 和-1来表示向上迁移、保持不变和向下迁移。
时刻的变速器档位迁移命令,分别用1,0 和-1来表示向上迁移、保持不变和向下迁移。
传动系的另一关键部件——离合器,负责把发动机的转矩和速度传递给变速器,有分离和闭合两种状态。分离状态时,发动机处于熄灭状态,只传递电机的输出转矩和速度到变速箱;闭合状态时,将发动机和电机的转矩与速度全部传递给变速箱。即:
| (14) |
以上部分为本项目能量管理策略设计中使用的车辆模型,为后续能量管理策略奠定基础。
2 基于动态规划的能量管理策略
2.1 能量管理最优问题提出
本项目将并联式混合动力汽车建模为离散时间动态系统,其状态转移如下:
| (15) |
其中,![]() 为
为![]() 时刻的状态矢量;
时刻的状态矢量;![]() 为决策集中选择的
为决策集中选择的![]() 时刻的控制矢量;
时刻的控制矢量;![]() 表示当前离散时间;
表示当前离散时间;![]() 为控制持续的时间。
为控制持续的时间。
能量管理最优化问题中,系统状态矢量为:![]() ,控制矢量为:
,控制矢量为:![]() 。
。
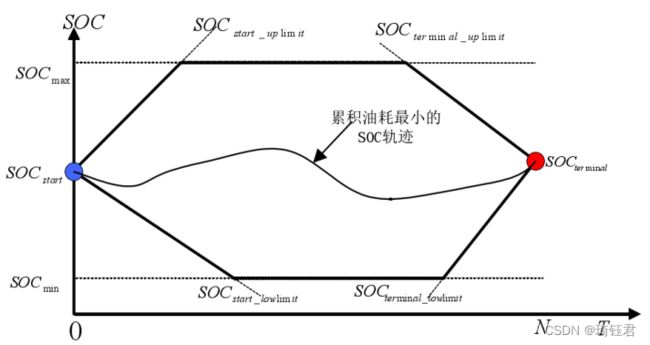
能量管理的目标是最大化燃油经济性的同时,保持循环工况内电池SOC在[0.4,0.7]的范围内。本项目定义能量管理策略为![]() ,可以根据
,可以根据![]() 选择控制动作
选择控制动作![]() 使车辆状态从
使车辆状态从![]() 更新到
更新到![]() 。其中,集合
。其中,集合![]() 为控制域。同时,定义值函数
为控制域。同时,定义值函数![]() 为从第
为从第![]() 个时刻到工况最终状态时,期望的累计代价,用于评价从
个时刻到工况最终状态时,期望的累计代价,用于评价从![]() 时刻到末端状态的策略。则
时刻到末端状态的策略。则![]() 为对策略
为对策略![]() 的评价。可以看出,最优策略
的评价。可以看出,最优策略![]() 的值函数为
的值函数为![]() 。由于无限时域的优化求取的策略具有时不变性,本项目将最优能量管理问题建模如下:
。由于无限时域的优化求取的策略具有时不变性,本项目将最优能量管理问题建模如下:
| (16) |
其中,![]() 为保证值函数收敛的折扣因子;
为保证值函数收敛的折扣因子;![]() 为阶段代价函数,其定义如下:
为阶段代价函数,其定义如下:
| (17) |
其中,![]() 和
和![]() 分别为
分别为![]() 时刻的燃油消耗、电池SOC变化的代价;
时刻的燃油消耗、电池SOC变化的代价;![]() 代表电池SOC的权重因子。
代表电池SOC的权重因子。
![]() 定义为
定义为![]() 时刻可能的电池SOC偏离循环工况末端电池荷电状态
时刻可能的电池SOC偏离循环工况末端电池荷电状态![]() 的代价。具体如下:
的代价。具体如下:
| (18) |
在求解最优控制问题时,车辆控制系统的约束为:
| (19) |
其中,![]() 和
和![]() 决定
决定![]() ;
;![]() 与电机功率相关。由电池SOC的递推公式可知,电机功率与有关。
与电机功率相关。由电池SOC的递推公式可知,电机功率与有关。
2.2 基于动态规划的能量管理策略求解
动态规划法基于贝尔曼最优化原理,被广泛应用于确定性条件下,按照阶段进行决策且具有无后效性的问题中。无后效性的意思为:若系统在某时刻的状态已知,那么该时刻以后系统状态的变化只与当前时刻有关,而与系统之前的状态无关。该原理认为如果![]() 是基本问题的最优策略,那么
是基本问题的最优策略,那么![]() 为从第
为从第![]() 个决策步状态到最后一个阶段状态的子问题的最优解。即:决策为
个决策步状态到最后一个阶段状态的子问题的最优解。即:决策为![]() 时,第
时,第![]() 个决策步状态到最后一个阶段状态的期望的累计代价函数为
个决策步状态到最后一个阶段状态的期望的累计代价函数为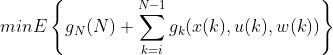 。其中,
。其中,![]() 为末端状态的代价;
为末端状态的代价; ![]() 为阶段
为阶段![]() 的阶段代价函数;
的阶段代价函数;![]() 、
、![]() 和
和 ![]() 分别为
分别为![]() 时刻的状态向量、控制向量和随机向量。
时刻的状态向量、控制向量和随机向量。
动态规划法的步骤一般为:首先确定每个决策步的所有可行状态域;然后计算出每个“状态-动作-状态”的阶段性代价,并将其存储在表格中;最后对最优问题按逆向或者正向阶段求解。
本文的能量管理问题中采用如下的逆向求解方程对能量管理问题求解
| (20) |
其中,![]() 为第
为第![]() 个决策步时的最优值函数。由于动态规划中,车辆工况是已知的,由此,每个决策步中车辆的状态向量中,驾驶员需求转矩和车轮角速度可以根据车辆逆向动力学模型得到。本项目的车辆状态转移方程具体为:
个决策步时的最优值函数。由于动态规划中,车辆工况是已知的,由此,每个决策步中车辆的状态向量中,驾驶员需求转矩和车轮角速度可以根据车辆逆向动力学模型得到。本项目的车辆状态转移方程具体为:
 |
(21) |
其中,![]() 为采样间隔。 由式(20)有,第
为采样间隔。 由式(20)有,第![]() 个决策步的最优控制矢量为:
个决策步的最优控制矢量为:
| (22) |
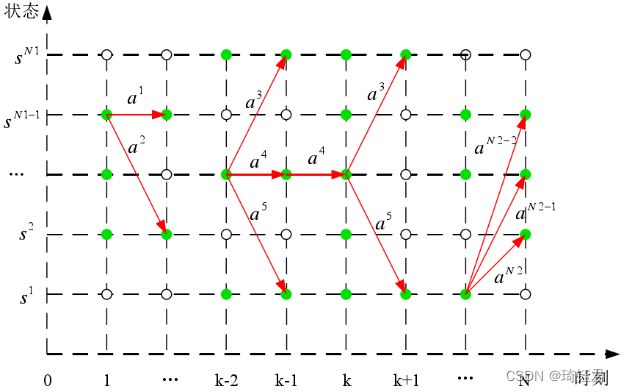
动态规划法的原理图如图6所示。其中,状态空间为:![]() ,动作空间为:
,动作空间为:![]() 。图中每一列心圆和绿色原点代表系统的状态空间。绿色的小圆点表示在该时刻状态的可选择范围。红色的箭头线条表示由
。图中每一列心圆和绿色原点代表系统的状态空间。绿色的小圆点表示在该时刻状态的可选择范围。红色的箭头线条表示由![]() 到
到![]() 时刻系统采取的控制动作。当用状态转移方程由
时刻系统采取的控制动作。当用状态转移方程由![]() 计算出
计算出![]() 的可行集时,用最近邻法则将
的可行集时,用最近邻法则将![]() 离散化到途中的状态空间中。
离散化到途中的状态空间中。
动态规划算法是一种数值运算的方法。状态空间和动作空间的选取,对算法的结果影响非常大。在具体实现中,我们首先对驾驶员的需求转矩进行数值分析,统计出,每个工况下需求转矩的出现频率,对于出现频率低的点,采用较低的离散精度,对于出现频率比较高的点,采用较细的离散精度。
3 仿真实验及结果分析
为验证基于动态规划的能量控制策略的优化效果,以典型循环工况为例进行仿真实验,设定电池SOC初始值为0.5。
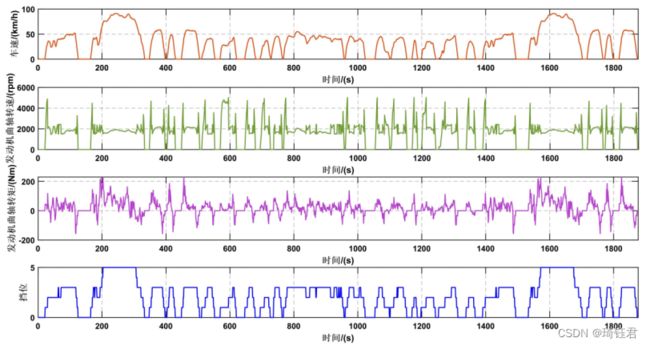
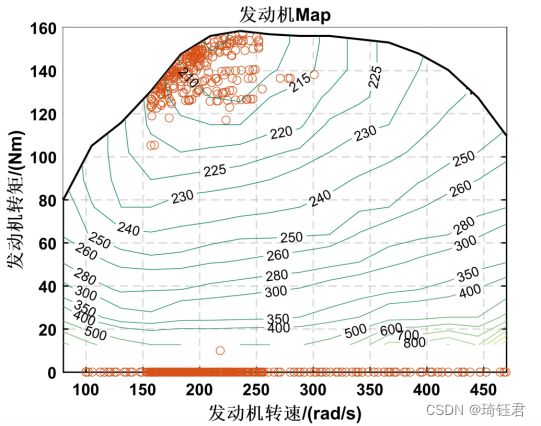
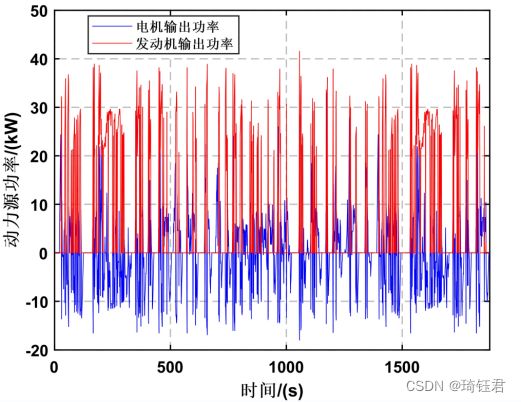
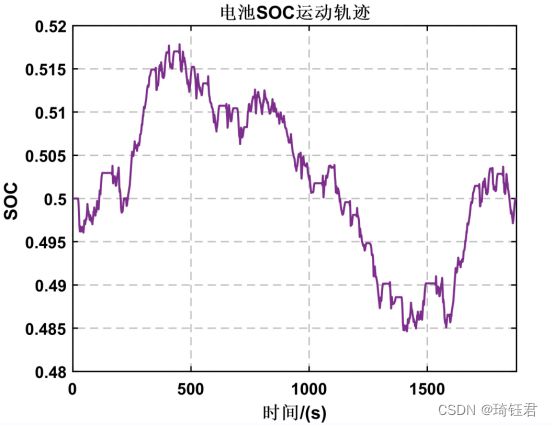
图9为车速跟随情况、发动机工作情况和挡位变化情况的曲线。图10 为发动机的工作点分布情况。图11为发动机和电机的输出功率情况。图12为电池SOC运动轨迹。
由图9-12可见,发动机基本都工作在经济区域,电池SOC保持在一定的范围之内。
4 结论
本项目以提高并联式混合动力汽车燃油经济性为目标,根据该系统结构特点和对控制策略的适应性要求,设计了以发动机转矩和变速器速比为控制变量,整车燃油消耗最小为目标的动态规划能量管理策略,并基于所建模型和策略进行了仿真。仿真结果表明:本项目所提出的控制策略的优化效果良好,发动机运行在高效区域内,电池能量也能保持平衡。