YOLO V4 详解
YOLO V4
论文地址:YOLOv4: Optimal Speed and Accuracy of Object Detection (arxiv.org)
主要改进
- Backbone中加入了CSP, SPP, PAN, 使用了 Mish activation function.
- 对坐标偏移的
sigmoid函数进行了缩放,让中心点能够相对容易的匹配极限位置0或者1. - 尝试了多种数据增强方法, mosaic, cut mix, label smoothing.
- 对于要拟合的预选框的调整,因为对坐标偏移的
sigmoid函数进行了缩放,因此在做正负样本匹配是基于IOU的值可以选择更多的cell. - Loss function 改进为 CIOU Loss.
Network structure improvement
Backbone: CSPDarknet53
CSP Module
论文地址:CSPNet: A New Backbone that can Enhance Learning Capability of CNN
优点:
-
增强CNN的学习能力
-
移除bottlenecks structure:
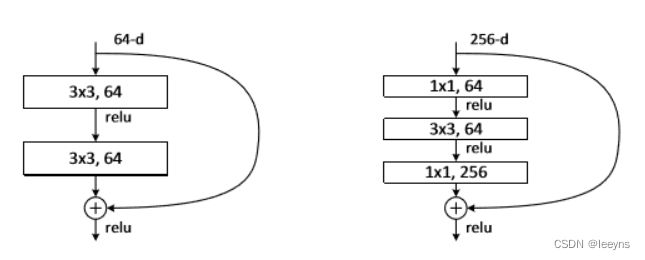
bottlenecks structure 出现在Resnet中,即对特征的通道数先减小后增大的操作。从而减少了计算的参数量并且能够增加网络的深度。左图没有使用bottlenecks结构,右图使用了。
-
降低显存的使用
实现方式是通过将浅层的feature map一分为二(这个分就是CSP中的P: Partial ),一半去经过block,一半是直接concat到block的output.
YOLO V4 CSPDarknet53中的CSP模块的结构如下:

YOLO V4 中的CSP模块:
不同于原始的CSP将浅层的特征一分为二,CSPDarknet53中是通过两个 1 * 1的卷积层将特征网络的通道减半,对于其中一半通道进行ResBlock等一系列的操作后,和另一半通道进行concat后再进行后续的卷积操作。
SPP Module
论文地址:Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition)
- 解决多尺度问题: 通过不同尺度的pooling,融合不同的特征信息。
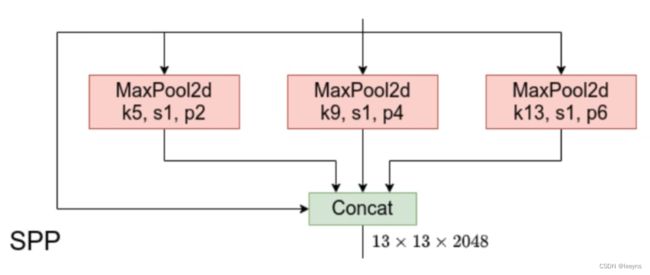
SPP模块由四个分支组成。为了保证Concatenate时候每个分支Tnesor的H和W相同,在进行 Maxpooling 时要进行不同程度的Padding,输入每个分支的输入和输出的shape是相同的。
PAN Module
论文地址: Path Aggregation Network for Instance Segmentation (arxiv.org)
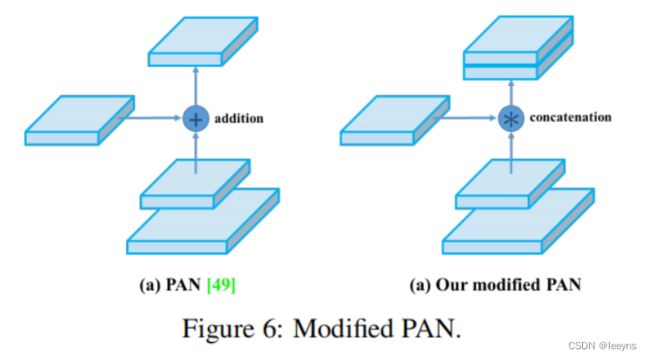
原文中的PAN模块结构如下:
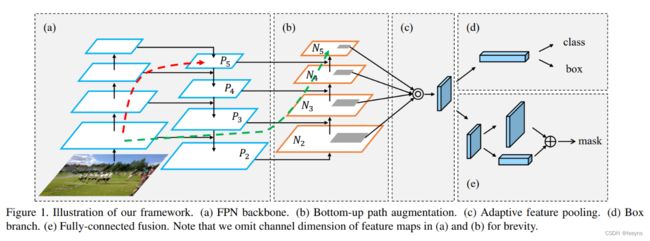
相对于FPN结构的将浅层特征和深层特征进行一次融合,PAN结构又进行了一次自下而上的特征的融合。
YOLO V4中的PAN模块,在特征融合的处理上和PAN有所不同,PAN是将两种特征进行相加,而YOLO V4中是将两种特征进行Concat。
Mish Activation function
YOLO V4 中的激活函数使用的是Mish 激活函数。
优化策略
坐标偏移的优化
在YOLO V3中坐标偏移的方法如下,公式中使用 sigmoid 函数将偏移量限制在 0-1 中。

但是 sigmoid 函数存在一个问题,即对于极限值不敏感 (需要输出值为0或者1的情况)。因此,在 YOLO V4 中对于偏移值的计算做出了改变,通过引入一个scale的参数。
b x = σ ( t x ) + c x b y = σ ( t y ) + c y \begin{aligned} b_x = \sigma(t_x) + c_x \\ b_y = \sigma(t_y) + c_y \\ \end{aligned} bx=σ(tx)+cxby=σ(ty)+cy
转换成:
b x = ( σ ( t x ) ⋅ s c a l e x y − s c a l e x y − 1 2 ) + c x b y = ( σ ( t y ) ⋅ s c a l e x y − s c a l e x y − 1 2 ) + c y \begin{aligned} b_x = (\sigma(t_x) \cdot scale_{xy} - \frac{scale_{xy}-1}{2}) + c_x \\ b_y = (\sigma(t_y) \cdot scale_{xy} - \frac{scale_{xy}-1}{2}) + c_y \\ \end{aligned} bx=(σ(tx)⋅scalexy−2scalexy−1)+cxby=(σ(ty)⋅scalexy−2scalexy−1)+cy
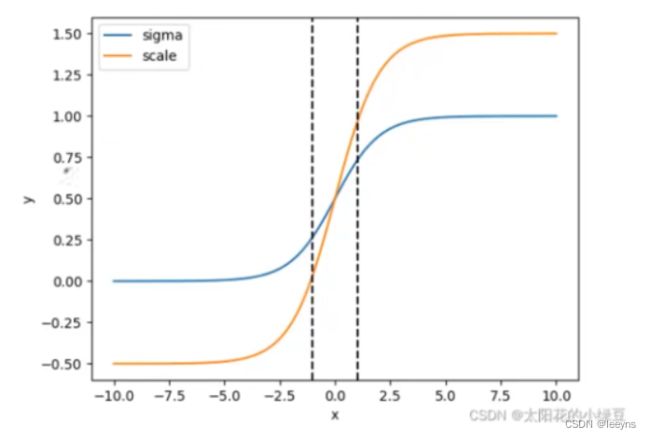
通过这样的操作可以将sigmoid的范围改变,一般将scale设为2,scale后的曲线如下图所示。
b x = ( 2 ⋅ σ ( t x ) − 0.5 ) + c x b y = ( 2 ⋅ σ ( t y ) − 0.5 ) + c y \begin{aligned} b_x = (2 \cdot \sigma(t_x) - 0.5) + c_x \\ b_y = (2 \cdot \sigma(t_y) - 0.5) + c_y \\ \end{aligned} bx=(2⋅σ(tx)−0.5)+cxby=(2⋅σ(ty)−0.5)+cy
Data augmentation
在YOLO V4中,作者实验验证了,CutMix, Mosaic, Label Smoothing, 对于性能的提升有了一定的帮助,如下表所示,红框的内容。

IOU阈值的选取
在YOLO V3中,对于正样本的选取是通过计算anchor与GT的IOU值,并取最大的一个IOU值对应的anchor作为正样本进行优化,这样会存在一个问题就是正样本的个数特别少,对于YOLO V3的优化中,有的办法是将所有大于IOU阈值的anchor都作为正样本来优化。
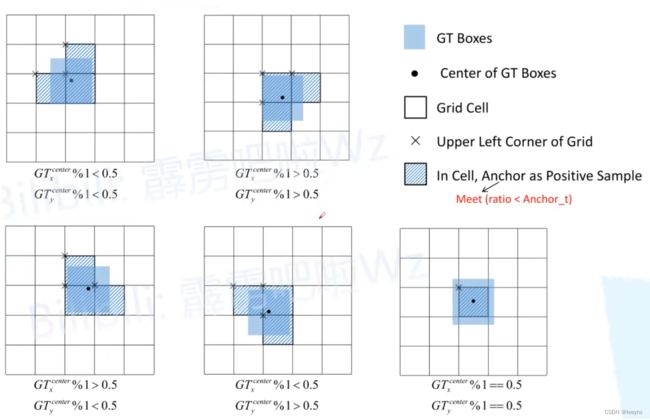
在YOLO V4中,因为对预测框的偏移值的改进,偏移值的范围从 0-1 变为了 -0.5 - 1.5. 因此,对于YOLO V4的正样本选取,除了最中心的cell的anchor会被选为正样本,附近两个cell的anchor同时会被选择成正样本。
Loss Function
YOLO V4 中,将预测框的损失函数由仅仅考虑x,y,w,h,变为考虑IOU Loss.
Loss function 的发展过程:
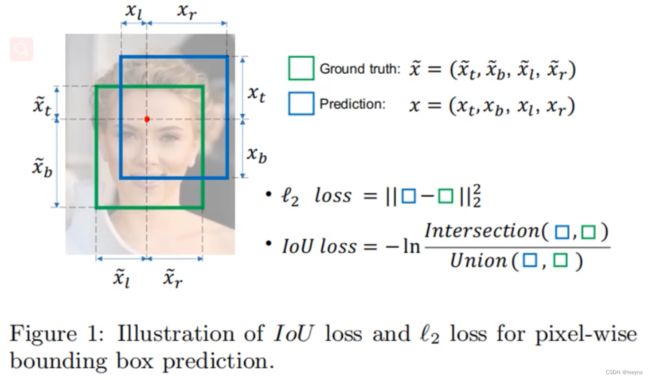
最开始YOLO V3 使用的定位损失函数是针对于预测框和GT的坐标值以及高宽进行的L2损失计算。这样计算损失的话,x, y, w, h都是相互独立的,然而实际情况中这四个值是存在某种关系的,所以不少的研究者就使用了IOU loss. 对于IOU loss存在的问题,进一步发展出了 GIOU, DIOU, CIOU loss.
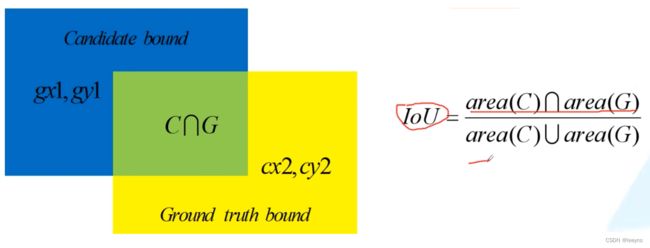
IOU的计算方式:
IOU Loss
优点:
- 能够更好的反应重合程度
- 具有尺度不变性
缺点:
- 当不相交时loss为0
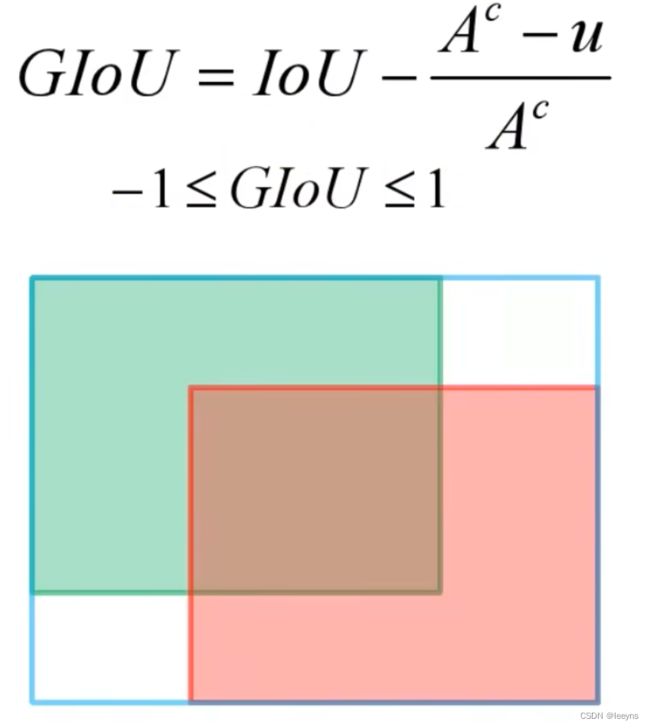
GIOU Loss
其中 A c A^c Ac 表示能够包含两个边界框最小的包围框的面积, u u u 表示两个边界框的并集的面积。GIoU的取值范围为[-1, 1],当两个边界框完全重合时GIoU的值为1,当两个边界框距离很远,此时GIoU的值为-1。
优点:
- 很好的解决了IoU loss在不相交时为0的问题。
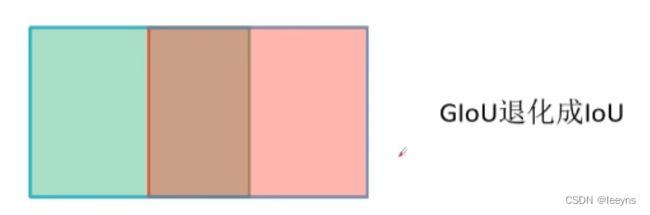
缺点:
DIoU Loss
论文地址:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression)
IoU 和 GIoU 存在的收敛比较慢以及回归的准确度比较低的问题。如下图,同样的训练轮次,第二行表示的是使用DIoU Loss训练的过程,可以发现DIoU Loss 收敛更快。
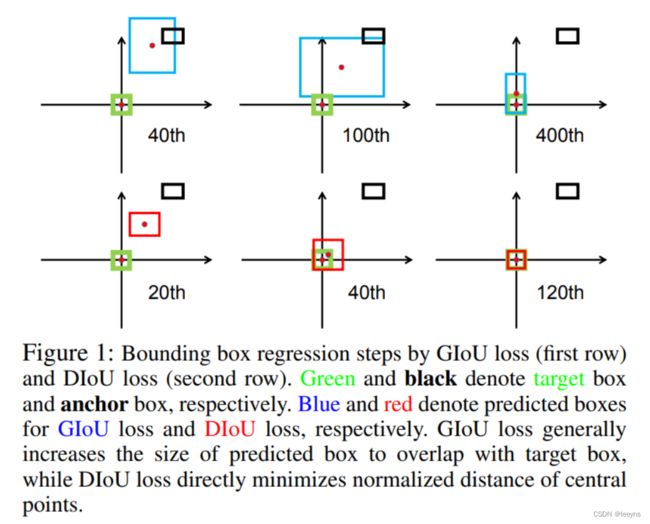
出现这样的情况是因为,IoU 和 GIoU 只能表达预测框和目标框之间的重合关系,但并不能很好的表达预测框和目标框之间的位置关系。如下图,可以看出,只有 DIoU 才能表示出两个框的位置关系。
DIOU 的计算公式如下:
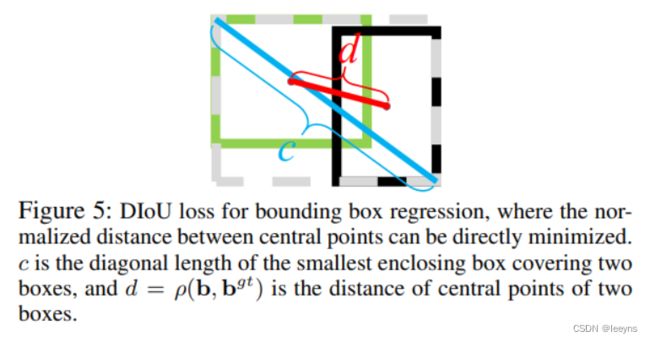
D I o U = I o U − ρ 2 ( b , b g t ) c 2 = I o U − d 2 c 2 − 1 ≤ D I o U ≤ 1 \begin{array}{c} D I o U=I o U-\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}=I o U-\frac{d^{2}}{c^{2}} \\ -1 \leq D I o U \leq 1 \end{array} DIoU=IoU−c2ρ2(b,bgt)=IoU−c2d2−1≤DIoU≤1
其中 c c c 表示两个框的中心点的距离, d d d 表示两个框的最小外接矩阵的对角线的长度。
DIOU Loss 能够直接最小化两个目标边界框之间的距离,所以能够更好的收敛。
CIOU Loss
DIOU Loss 同时存在问题,它只能表征两个框的重叠面积,中心点的距离。但是,一个好的定位框损失函数也应该考虑框的长宽比。因此,CIOU 则在DIOU的基础上加入了长宽比的信息。
C I o U = I o U − ( ρ 2 ( b , b g t ) c 2 + α v ) v = 4 π 2 ( arctan w g t h g t − arctan w h ) 2 α = v ( 1 − I o U ) + v \begin{array}{c} C I o U=I o U-\left(\frac{\rho^{2}\left(b, b^{g t}\right)}{c^{2}}+\alpha v\right) \\ v=\frac{4}{\pi^{2}}\left(\arctan \frac{w^{g t}}{h^{g t}}-\arctan \frac{w}{h}\right)^{2} \\ \alpha=\frac{v}{(1-I o U)+v} \end{array} CIoU=IoU−(c2ρ2(b,bgt)+αv)v=π24(arctanhgtwgt−arctanhw)2α=(1−IoU)+vv