R语言-时间序列实验

数据

数据选取的是2013年某餐饮的销售额。提取链接如下：
链接: link
提取码：1234

实验目的及内容

目的

1． 掌握时间序列的常用算法的建模及预测过程。

内容

1．时间序列的平稳性检验
绘制时间序列图、自相关检验、偏自相关检验、单位根检验、白噪声检验。
2．时间序列建模分析
非平稳时间序列处理、模型识别定阶、残差白噪声检验。
3.时间模型序列模型预测
时间序列模型预测绘制时间序列发展趋势图。

实验

导入数据并对数据进行查看，并创建时间序列。

#导入数据，并查看数据前五行
mydata<-read.csv('D:\\学习文档\\R语言\\\\arima_data.csv',header = TRUE)
head(mydata)
#创建时间序列对象
is.ts(mydata)
sales1=ts(mydata$sales)
is.ts(sales1)


sales2=as.ts(mydata$sales)
is.ts(sales2)

1.时间序列的平稳性检验

（1）绘制时间序列图对数据平稳性进行检
根据平稳时间序列的均值和方差都为常数的性质，平稳序列的时序图显示该序列值始终在一个常数附近随机波动，而且波动范围有界；如果有明显的趋势性或者周期性，那通常不是平稳序列。

plot.ts(sales2,xlab="date",ylab="sales")

很明显该序列有明显的趋势性，所以不是平稳序列。

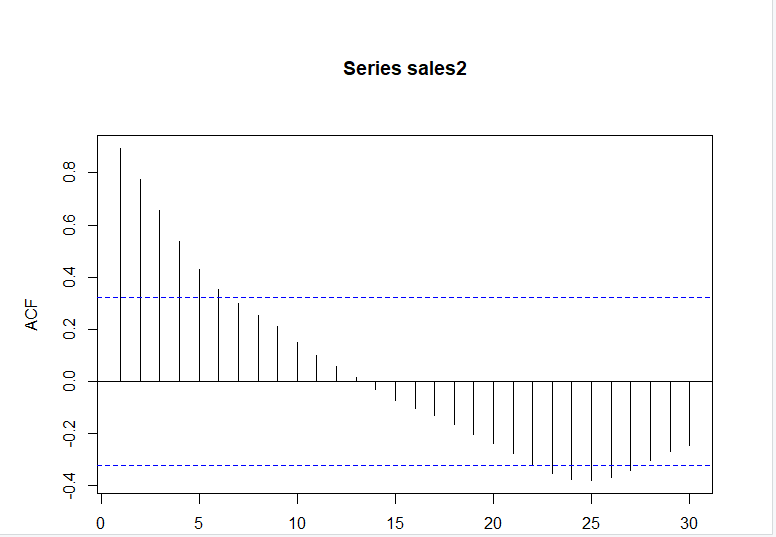
（2）自相关性检验
自相关图中的两天虚线表示置信界限是自相关系数的上下界。如果自相关系数迅速衰减落入置信区间内，就可能是白噪声；如果自相关系数超出置信区间，那么表示存在相关关系。

acf(sales2,lag.max = 30)

存在相关性关系
（4）偏自相关检验

pacf(sales2,lag.max = 30)

（3）单位根检验
返回的P值小于0.05表示满足单位根检验

install.packages("fUnitRoots")
library(fUnitRoots)
unitrootTest(sales1)

2.时间序列建模分析

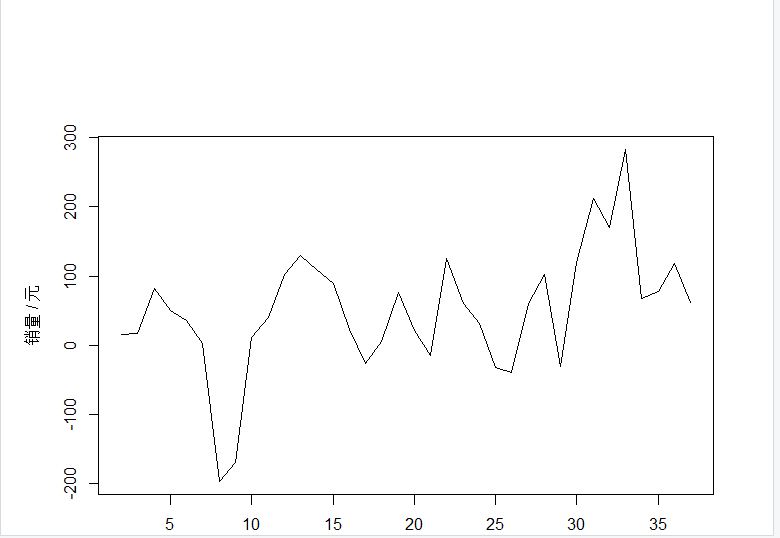
（1）非平稳序列差分

#一阶差分平稳检验
difsales= diff(sales1)
plot.ts(difsales,xlab="日期",ylab="销量 / 元")

（2）一阶差分自相关检验

acf(difsales,lag.max = 30)

（3）一阶差分单位根检验

unitrootTest(difsales)

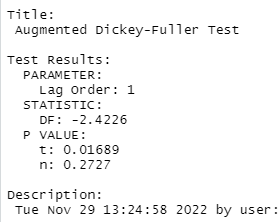
p-value<0.05符合单位根检验
（4）时间序列模型识别定阶

install.packages("TSA")
library(TSA)
res<-armasubsets(y=difsales,nar=5,nma=5,y.name='test',ar.method='ols')
plot(res) 

根据BIC图可以发现，BIC值从下往上，依次递减。模型选用变量的单元格用阴影表示。较好的模型（具有较低BIC值）出与较高的行中。第一行test-lagl被选入模型，error-lagl到error-lagl均未被选中，取零阶，即在test-lagl、error-lag0处取BIC最小值，即当p=1，q=0时，BIC值最小。即对原始序列建立ARIMA（1，1，0）模型。

library(stats)
arima=arima(sales1,order=c(1,1,0))
arima

（5）白噪声检验

Box.test(arima$residuals,lag = 5,type = "Ljung-Box")

p-value>0.05通过白噪声检验

3.时间模型序列模型预测

（1）模型预测

install.packages("forecast")
library(forecast)
forecast<-forecast(arima,h=5,level=c(80,95))
forecast

这样模型会报错，无法辨认arima是arima函数还是stats内部的函数需做以下更改。

install.packages("forecast")
library(forecast)
arima=stats::arima(sales1,order = c(1,1,0))
forecast<-forecast(arima,h=5,level=c(80,95))
forecast

（2）绘制原始值与预测图形

plot.forecast(forecast)

这里也会报错，只找到一种解决办法。将代码换成下面就可以了

library(ggplot2)
autoplot(forecast)